單位根模型的復(fù)合分位數(shù)自回歸推斷

徐 成,龐天曉

(浙江大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,浙江杭州 310027)

§1 引言

許多經(jīng)濟(jì)學(xué)和金融學(xué)的文獻(xiàn)指出:由于經(jīng)濟(jì)和金融中的隨機(jī)變量通常具有非平穩(wěn)性,因此很多經(jīng)濟(jì)時間序列數(shù)據(jù)用單位根模型或者近單位根模型來建模比較合適.在過去的幾十年,單位根模型和近單位根模型一直受到許多學(xué)者的關(guān)注,見Dickey和Fuller[1],Phillips[2]以及Phillips和Magdalinos[3]等文獻(xiàn).在單位根模型中,自回歸系數(shù)等于1,而近單位根模型中的自回歸系數(shù)通常假設(shè)接近1,并隨樣本容量大小而變化.近單位根模型形式多樣.例如,Phillips[2]假設(shè)自回歸系數(shù)ρ=ρn=1-c/n,其中c是一個常數(shù),n是樣本容量,這個模型可看成是單位根模型的推廣,它在平穩(wěn)一階自回歸模型和單位根模型之間建立了一座橋梁;Phillips和Magdalinos[3]建議取ρ=ρn=1-c/kn,其中c/=0,而kn是滿足kn=o(n)的一個發(fā)散到正無窮的正常數(shù)序列.當(dāng)c ＞0時,這個模型在平穩(wěn)一階自回歸模型和剛才的近單位根模型之間建立了一座橋梁;當(dāng)c ＜0時,這個模型在單位根模型和爆炸模型(即自回歸系數(shù)是大于1的常數(shù))之間建立了一座橋梁.Phillips和Magdalinos[3]提出的這個模型在金融市場的泡沫現(xiàn)象的統(tǒng)計(jì)建模中有重要的應(yīng)用,可用來描述泡沫的膨脹過程和破滅過程,見Phillips和Shi[4].對于此類非平穩(wěn)自回歸模型,參數(shù)估計(jì)和假設(shè)檢驗(yàn)是學(xué)者關(guān)注的主要課題.本文關(guān)注單位根模型的估計(jì)問題.

有很多方法可以用來估計(jì)自回歸系數(shù),例如最小二乘法和極大似然法.但是,當(dāng)模型誤差不是高斯分布時,這些方法通常不夠穩(wěn)健.也就是說,當(dāng)遇到具有異常值或重尾特征的數(shù)據(jù)時,這些估計(jì)方法不夠穩(wěn)健.因此,需要尋找一些穩(wěn)健的估計(jì)方法.在這個研究方向上,許多學(xué)者提出了各種穩(wěn)健估計(jì)方法,例如Knight[5]和Herce[6].Koenker和Xiao[7]提出了單位根模型的分位數(shù)自回歸估計(jì)方法.分位數(shù)方法最先是由Koenker和Bassett[8]提出的,用于估計(jì)線性回歸模型中的回歸系數(shù).與傳統(tǒng)的最小二乘法相比,分位數(shù)方法研究因變量的各種條件分位數(shù),而最小二乘法只研究因變量的條件平均趨勢.在Koenker和Xiao[7]中,當(dāng)模型誤差偏離高斯條件時,分位數(shù)自回歸估計(jì)方法在穩(wěn)健性方面被證明是優(yōu)于其他很多現(xiàn)有方法的.受這一發(fā)現(xiàn)的啟發(fā),Zhou和Lin[9]成功地將分位數(shù)自回歸方法應(yīng)用于Phillips和Magdalinos[3]提出的近單位根模型.值得注意的是,在Koenker和Xiao[7]和Zhou和Lin[9]中,他們都只使用了一個分位點(diǎn).

顯然,分位數(shù)回歸方法只使用了樣本的局部信息.若分位點(diǎn)選擇不當(dāng),分位數(shù)估計(jì)可能有不理想的估計(jì)偏差和估計(jì)精度.Zou和Yuan[10]提出了復(fù)合分位數(shù)回歸方法,他們建議在統(tǒng)計(jì)推斷中使用多個分位點(diǎn)而不是一個分位點(diǎn),這樣就會有更多的樣本信息被用來進(jìn)行統(tǒng)計(jì)推斷.Zou和Yuan[10]指出:當(dāng)模型誤差偏離高斯條件時,這個方法可以比最小二乘法好很多.實(shí)際上,通過數(shù)值模擬他們發(fā)現(xiàn):復(fù)合分位數(shù)回歸方法在估計(jì)偏差和估計(jì)精度方面具有很大的優(yōu)勢.根據(jù)Zou和Yuan[10]的建議,倪和傅[11]用復(fù)合分位數(shù)自回歸方法估計(jì)了Phillips和Magdalinos[3]提出的近單位根模型中的自回歸系數(shù),通過模擬分析,他們發(fā)現(xiàn):復(fù)合分位數(shù)自回歸估計(jì)比分位數(shù)自回歸估計(jì)有更小的估計(jì)偏差和更好的估計(jì)精度.本文的目的是使用復(fù)合分位數(shù)自回歸方法估計(jì)單位根模型中的自回歸系數(shù).

本文結(jié)構(gòu)如下.§2提出單位根模型的復(fù)合分位數(shù)自回歸估計(jì),并研究此估計(jì)量的大樣本性質(zhì).§3通過Monte Carlo模擬評估復(fù)合分位數(shù)自回歸估計(jì)在有限樣本情形下的表現(xiàn).§4給出了一個實(shí)證分析.§5對該文進(jìn)行了總結(jié).單位根模型的復(fù)合分位數(shù)自回歸估計(jì)的漸近理論的證明放在§6.§7研究了增廣的Dickey-Fuller模型(ADF模型),并討論了該模型中的復(fù)合分位數(shù)自回歸估計(jì)的漸近理論.

§2 模型和結(jié)論

首先介紹本文接下來需要用到的一些記號.“?”表示概率測度弱收斂,“ p-→”表示依概率收斂,“ d-→”表示依分布收斂,“[nr]”表示nr的整數(shù)部分,“:=”和“=:”表示等價(jià)定義,上標(biāo)“T”表示向量或矩陣的轉(zhuǎn)置,“I(·)”表示示性函數(shù).除非另有說明,本文中的極限均理解為n →∞.

設(shè){yt,t ≥0}來自一階自回歸時間序列模型:

其中,{ut,t ≥1}是模型誤差.在這個模型中,當(dāng)α1=1時,(1)就是一個單位根模型.把由{us,s ≤t}生成的σ-域記為Ft,設(shè)0＜τ1＜τ2＜……·＜τK ＜1為K個分位點(diǎn),其中K ∈N.記ut的τk-條件分位數(shù)為Qu(τk),并記yt對于Ft-1的τk-條件分位數(shù)為Qyt(τk|Ft-1).那么,下式成立:

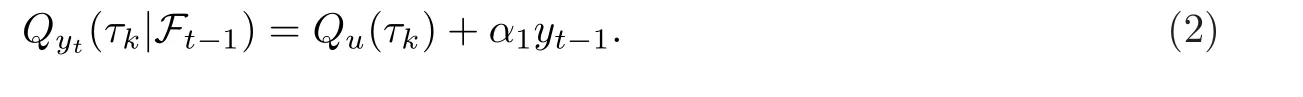
記α0(τk)=Qu(τk),k=1,……,K.則(α0(τ1),……,α0(τK),α1)的復(fù)合分位數(shù)自回歸估計(jì)定義為

其中,ρτk(u)=u(τk-I(u ＜0)).

本文關(guān)注α1=1時的統(tǒng)計(jì)推斷.考慮到金融時間序列數(shù)據(jù)普遍具有重尾的性質(zhì),與Zhou和Lin[9]以及倪和傅[11]一樣,本文假設(shè){ut,t ≥1}是一屬于正態(tài)吸引場的獨(dú)立同分布(i.i.d.)隨機(jī)變量序列.對于模型(1),作如下兩個假設(shè).

· 假設(shè)1是一屬于正態(tài)吸引場的i.i.d.隨機(jī)變量序列,均值為0,方差可能無窮大.

在假設(shè)1中,由于{ut,t ≥1}的方差可能不存在,引入截尾的技巧.令

其中{W(r),0≤r ≤1}是一個標(biāo)準(zhǔn)維納過程.根據(jù)Cs¨org?o等[12]的式子(18),有

的部分和服從弱不變原理(參見Phillips和Durlauf[16]的Corollary 2.2):

結(jié)合(5)和(6),得

然后,根據(jù)Hansen[17]的Theorem 2.1,得

注1.由(6),(·)是一個布朗運(yùn)動,且

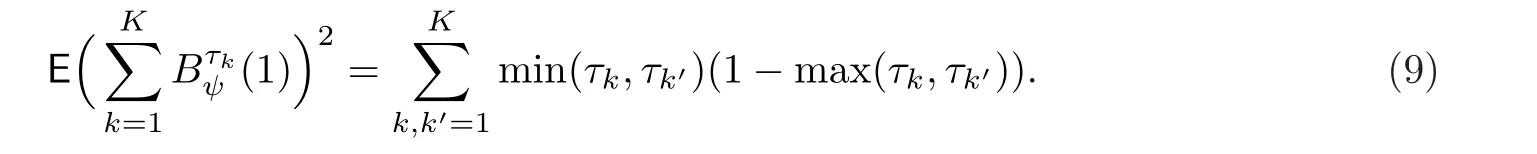
2.根據(jù)Zou和Yuan[10]的建議,在實(shí)際應(yīng)用中,為了方便起見可以等間隔地選取分位點(diǎn),即取τk=k/(K+1).對于這樣的取法,通過一些簡單的計(jì)算,可知

下面的定理給出了模型(1)中α1的復(fù)合分位數(shù)自回歸估計(jì)的收斂速度和極限分布.

定理2.1假設(shè){yt,t ≥1}來自模型(1),其中α1=1.若假設(shè)1和2被滿足,那么有

推論2.1假設(shè){yt,t ≥1}來自模型(1),其中α1=1.若假設(shè)1和2被滿足,那么有

在假設(shè)1中并未要求{ut,t ≥1}的方差一定存在.若{ut,t ≥1}的方差存在,則有以下推論:

推論2.2假設(shè){yt,t ≥1}來自模型(1),其中α1=1.若假設(shè)1和2被滿足,且0＜Var(ut)=σ2＜∞,那么有

注 若K=1時,即只使用一個分位點(diǎn),不妨記為τ,那么由推論2.2可得

這正是Koenker和Xiao[7]里的結(jié)論.

接下來,研究α1的復(fù)合分位數(shù)自回歸估計(jì)與分位數(shù)自回歸估計(jì)的漸近相對有效性.只需計(jì)算如下的比值大小:

若上述比值大于1,則說明復(fù)合分位數(shù)自回歸估計(jì)在估計(jì)有效性方面優(yōu)于分位數(shù)自回歸估計(jì).為了便于計(jì)算,假設(shè)ut～N(0,1),τ=0.5(相應(yīng)的分位數(shù)估計(jì)就是常見的最小絕對偏差估計(jì)),并取τk=k/(K+1).在這種情況下,根據(jù)Zou和Yuan[10]的Theorem 3.1,有

若取ut～t(3),τ=0.5,根據(jù)Zou和Yuan[10]的Corollary 3.1,經(jīng)過一些簡單的計(jì)算可得

在實(shí)際中,需要選擇合適的K值.根據(jù)(10)式以及參考Zou和Yuan[10]中關(guān)于漸近有效性的討論(該文中第三章節(jié)),對于不同的K值,把的方差,即

的大小列于表1(該值越小,意味著復(fù)合分位數(shù)方法越有效),其中,ut=∈t-E(∈t),∈t來自以下7個分布:N(0,1),N(0,10),t(2),t(3),F(4,4),χ2(20),Beta(0.5,0.5).在ut的7個分布中,既有輕尾分布,也有重尾分布、非對稱分布.從表1可以看出,總的來說,K越大,復(fù)合分位數(shù)估計(jì)方法的表現(xiàn)將會越好.

表1 具體數(shù)值比較

在實(shí)際中,還需要考慮估計(jì)方法的計(jì)算成本.在本模型中,考慮不同的K值所對應(yīng)的估計(jì)方法所需的計(jì)算時間.通過R軟件中的proc.time來提取計(jì)算時間.取ut～N(0,1),樣本容量取為200,模擬的重復(fù)次數(shù)取為10000,將計(jì)算時間列于表2(在該表中,LS表示最小二乘法,QAR表示分位數(shù)自回歸方法,CQARK表示采用K個分位點(diǎn)的復(fù)合分位數(shù)自回歸方法).若實(shí)際工作者除了考慮估計(jì)有效性,還在乎計(jì)算成本,那么可對表1和表2進(jìn)行綜合分析,選擇K值.若選擇K=19,此時均勻的分位點(diǎn)分別是5%,10%,15%,……·,95%.

表2 不同K值的平均計(jì)算時間

§3 模擬

在本節(jié)中,通過Monte Carlo實(shí)驗(yàn)比較α1(其真值為1)的復(fù)合分位數(shù)自回歸估計(jì)、分位數(shù)自回歸估計(jì)以及最小二乘估計(jì)在有限樣本情形下的表現(xiàn).此外,將通過假設(shè)模型誤差為N(0,1)或t(2)來分析α1的復(fù)合分位數(shù)自回歸估計(jì)的有限樣本分布與極限分布的吻合程度.其中,N(0,1)具有有限方差,而t(2)的方差不存在.

記α1的K-復(fù)合分位數(shù)估計(jì)為,同時記α1的最小二乘估計(jì)和分位數(shù)自回歸估計(jì)為.根據(jù)定理2.1,α1的復(fù)合分位數(shù)自回歸估計(jì)的極限分布由下式刻畫:

根據(jù)Hamilton[18]以及Koenker和Xiao[7]中的結(jié)論,的極限分布分別由

為了簡單起見,以下Monte Carlo實(shí)驗(yàn)的復(fù)合分位點(diǎn)都是均勻取值(即取為τk=k/(K+1),k=1,……,K),y0取為0;{ut,t ≥1}由ut=∈t -E(∈t)產(chǎn)生,其中∈t分別取為N(0,1),t(2),F(4,4),χ2(20),Beta(0.5,0.5)分布.對于分位數(shù)自回歸估計(jì),只考慮τ=0.25,0.5,0.75的三種情況.而對于復(fù)合分位數(shù)自回歸估計(jì),考慮K ∈{2,5,9,19,49}這些情形.在以下所有的實(shí)驗(yàn)里,樣本容量n取為200,模擬的重復(fù)次數(shù)取為N=10000.

用QARτ表示取τ分位點(diǎn)的分位數(shù)自回歸估計(jì),CQARK的含義前面已給出說明.表3給出了三種估計(jì)方法在有限樣本情形下的表現(xiàn),括號內(nèi)的數(shù)字表示均方誤差.從表中可以看出:(1)當(dāng)誤差分布是正態(tài)分布時,最小二乘法在估計(jì)偏差和估計(jì)精度方面都具有最佳的有限樣本表現(xiàn).這是因?yàn)樵谡龖B(tài)情形下,最小二乘估計(jì)就是極大似然估計(jì).(2) 無論模型誤差是重尾分布還是非對稱分布,復(fù)合分位數(shù)自回歸方法在估計(jì)偏差和估計(jì)精度方面都優(yōu)于最小二乘法.(3) 總的來說,當(dāng)誤差分布是非對稱分布時,復(fù)合分位數(shù)自回歸方法比分位數(shù)自回歸方法更加穩(wěn)健.(4) 總的來說,對于復(fù)合分位數(shù)自回歸方法,當(dāng)分位點(diǎn)個數(shù)K增大時,復(fù)合分位數(shù)自回歸估計(jì)的有限樣本表現(xiàn)越來越好.總之,當(dāng)模型誤差偏離高斯條件時,復(fù)合分位數(shù)自回歸估計(jì)方法在估計(jì)偏差和估計(jì)精度方面要優(yōu)于最小二乘法和分位數(shù)自回歸方法.

表3 不同誤差分布假設(shè)下, α1的各種估計(jì)量在有限樣本情形下的表現(xiàn)

接下來假設(shè)模型誤差為N(0,1)或t(2),然后比較的有限樣本分布與極限分布的吻合程度.由定理2.1知

考慮到t(2)的方差不存在,采用推論2.1的表達(dá)式:

然后分析統(tǒng)計(jì)量Υn的有限樣本分布與它的極限分布的吻合程度.取樣本容量n=200,模擬重復(fù)次數(shù)為100000次.圖1和圖2分別給出了當(dāng)模型誤差為N(0,1)和t(2)時Υn的有限樣本分布與極限分布.從這兩張圖中可以看出:(1) Υn的有限樣本分布與極限分布是非常吻合的;(2) 類似于最小二乘估計(jì),復(fù)合分位數(shù)自回歸估計(jì)(經(jīng)過規(guī)范化后)的極限分布是左偏的.

圖1 模型誤差為N(0,1)時Υn的有限樣本分布(實(shí)線)與極限分布(虛線)

圖2 模型誤差為t(2)時Υn的有限樣本分布(實(shí)線)與極限分布(虛線)

§4 實(shí)證分析

從美國商務(wù)部經(jīng)濟(jì)統(tǒng)計(jì)局(BEA)下載了美國從1947年第1季度到2008年第4季度的季度GDP數(shù)據(jù)(單位:億美元).考慮季度GDP數(shù)據(jù)的對數(shù)序列.如圖3所示,該序列表現(xiàn)出上升趨勢,圖4給出了一階差分序列的時序圖,該差分序列看起來在一個固定的水平附近波動.為了證實(shí)所觀測到的現(xiàn)象,對該對數(shù)序列進(jìn)行了增廣的Dickey-Fuller單位根檢驗(yàn)(相應(yīng)的模型見(22)),當(dāng)q=1時,檢驗(yàn)統(tǒng)計(jì)量(見Hamilton[18],第523-524頁)的樣本值為-1.36364,相應(yīng)的p值為0.5489,因此在0.05的顯著水平下,單位根假設(shè)不能被拒絕.還選取了一些不同的q值(包括q=0,此時對應(yīng)于普通的單位根模型),都沒有改變假設(shè)檢驗(yàn)的結(jié)論(q=0時,p值為0.3634).

圖3 對數(shù)GDP序列的時序圖

圖4 對數(shù)GDP一階差分序列的時序圖

因此,可以假設(shè)該對數(shù)GDP序列來自普通的單位根模型或者增廣的Dickey-Fuller模型.不妨假設(shè)該數(shù)據(jù)來自普通的單位根模型:yt=α1yt-1+ut,α1=1.對于該樣本數(shù)據(jù),分別用最小二乘法,分位數(shù)自回歸估計(jì)方法和復(fù)合分位數(shù)自回歸估計(jì)方法對參數(shù)α1進(jìn)行統(tǒng)計(jì)推斷.對于分位數(shù)自回歸估計(jì),考慮τ=0.25,0.50,0.75的三種情況.而對于復(fù)合分位數(shù)自回歸估計(jì),選取K ∈{2,5,9,19}這4種情形.在獲得參數(shù)α1的估計(jì)量后,用來比較各個模型的均方誤差的大小,其中yt為真值,為模型擬合值,樣本容量T=248.計(jì)算結(jié)果見表4.可以發(fā)現(xiàn)估計(jì)值都比較接近1,而復(fù)合分位數(shù)自回歸估計(jì)方法的均方誤差要普遍小于最小二乘估計(jì)和分位數(shù)估計(jì)的均方誤差.這意味著,從數(shù)據(jù)與模型的吻合度考慮,復(fù)合分位數(shù)自回歸估計(jì)方法具有一定的優(yōu)勢.

表4 不同估計(jì)方法的表現(xiàn)

§5 結(jié)論

本文利用Zou和Yuan[10]提出的復(fù)合分位數(shù)估計(jì)方法研究了單位根模型中的自回歸系數(shù)的統(tǒng)計(jì)推斷.得到了復(fù)合分位數(shù)自回歸估計(jì)的漸近性質(zhì),并通過Monte Carlo模擬比較了復(fù)合分位數(shù)自回歸估計(jì)與最小二乘估計(jì)和分位數(shù)自回歸估計(jì)在有限樣本情形下的表現(xiàn).模擬結(jié)果表明,當(dāng)模型誤差偏離高斯條件時,復(fù)合分位數(shù)自回歸估計(jì)在估計(jì)偏差和估計(jì)精度方面都要優(yōu)于最小二乘估計(jì)和分位數(shù)自回歸估計(jì).此外,分析了美國季度GDP數(shù)據(jù)的對數(shù)序列,分析表明:從數(shù)據(jù)與模型的吻合度考慮,用復(fù)合分位數(shù)估計(jì)方法進(jìn)行統(tǒng)計(jì)推斷是合適且具有一定優(yōu)勢的.

§6 證 明

在本節(jié)中,將給出定理2.1的證明.首先,給出一個引理.

引理6.1設(shè)yt由模型(1)生成,其中α1=1.在假設(shè)1的條件下,有:

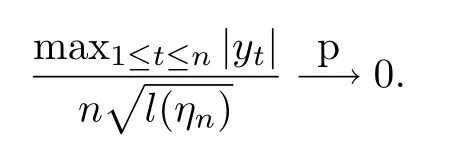
由正態(tài)吸引場隨機(jī)變量的泛函中心極限定理,

定理2.1的證明下面這個恒等式(參考Knight[5])在證明中扮演重要的作用:

應(yīng)用等式(11)可得

接下來,分別處理等式(12)中等號右側(cè)的各項(xiàng).

首先考慮(12)中等號右側(cè)的前兩項(xiàng).注意到(6)和(8)聯(lián)合成立,于是應(yīng)用Hansen[17]的Theorem 2.1,可得

注意到v1,v2是事先取定的有限值,所以根據(jù)引理6.1,對于任意的1≤k ≤K,

因?yàn)镵是固定的,所以

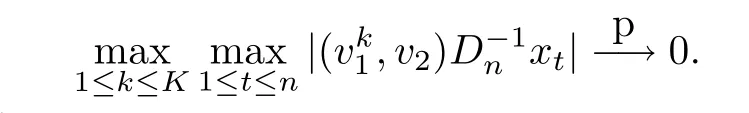
因此利用假設(shè)2和(15),有

將(14),(16)以及(18)結(jié)合在一起,可得

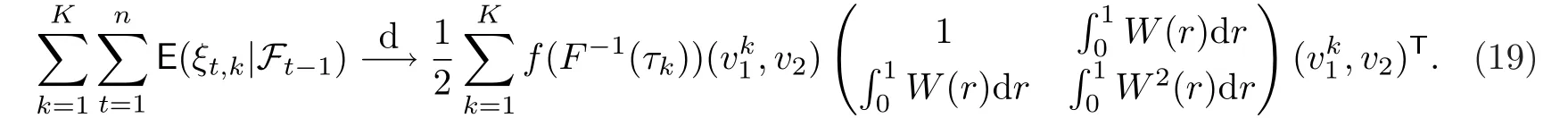
檢查以上的證明過程,可以發(fā)現(xiàn)下式也成立:

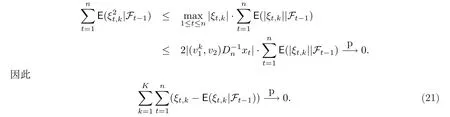
不難看出(13),(19)和(21)是聯(lián)合收斂的.于是

經(jīng)過簡單的計(jì)算,可知Z的極小值點(diǎn)為

那么,根據(jù)Knight[14]的Lemma A,可得

§7 推 廣

7.1 模型與漸近理論

在本節(jié)中,將模型(1)推廣至Dickey和Fuller[1]提出的增廣的Dickey-Fuller模型(ADF模型),并研究此模型的復(fù)合分位數(shù)自回歸估計(jì)的漸近理論.ADF模型表述如下:

其中,α1=1,Δ是差分算子,L是滯后算子,ut是模型誤差.

對ADF模型(22),作如下的兩個假設(shè).

· 假設(shè)1’的根都在單位圓外,是一個屬于正態(tài)吸引場的i.i.d.隨機(jī)變量序列,均值為0,方差可能無窮大.

· 假設(shè)2’{ut,t ≥1}的分布函數(shù)F(·)有連續(xù)的Lebesgue密度函數(shù)f(·),且在集合{x:0＜F(x)＜1}上滿足0＜f(x)＜∞.此外,假設(shè)supx∈R|f′(x)|＜∞.

那么,yt關(guān)于Ft-1的τk-條件分位數(shù)為

容易看出

把(α0(τ1),……,α0(τK),α1,……,αq+1)的復(fù)合分位數(shù)自回歸估計(jì)定義為

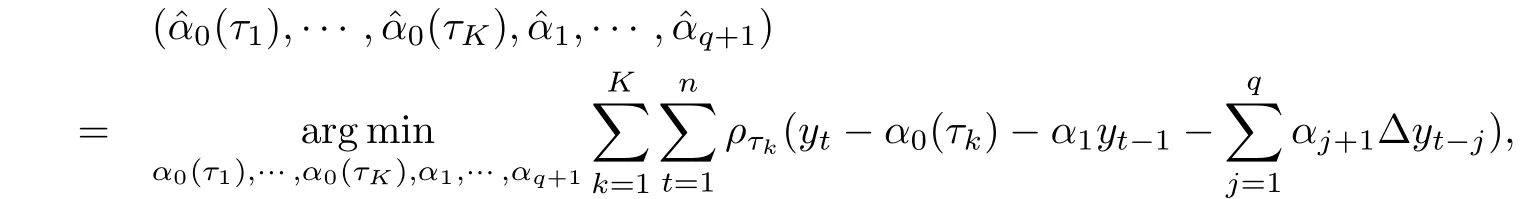
其中ρτk(u)=u(τk-I(u ＜0)).

那么,容易看出

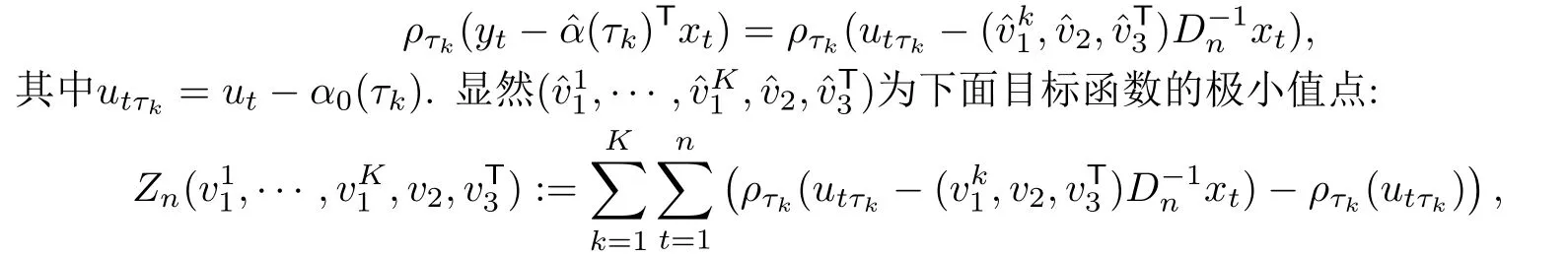
為了記號簡便,記

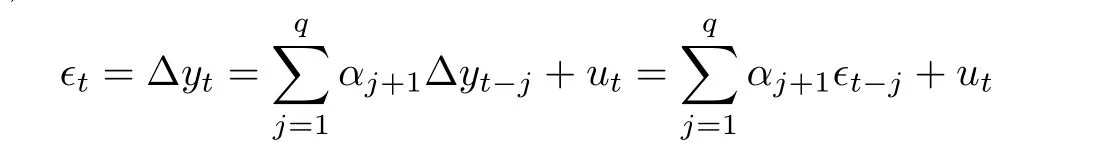
及ψτk(u)=τk-I(u ＜0).容易看出,由假設(shè)1’,{∈t,t ≥1}是來自正態(tài)吸引場的平穩(wěn)AR(p)過程,但它的方差可能不存在.因此對它應(yīng)用截尾技巧:

類似于(7)的推導(dǎo),通過上述的截尾技巧和Phillips和Durlauf[16]的Corollary 2.2,可得

那么,對于模型(22),有如下的漸近理論:

定理7.1假設(shè){yt,t ≥1}來自模型(22),其中α1=1.若假設(shè)1’和2’被滿足,那么有

7.2 證明

接下來分別處理等式(25)右邊的四項(xiàng).

對于等式(25)右邊的第一項(xiàng),直接應(yīng)用結(jié)論(24)可得

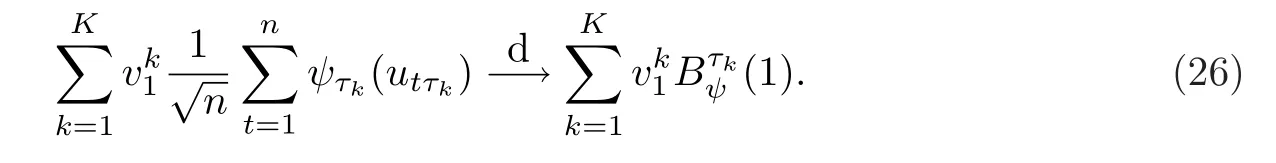
對于等式(25)右邊的第二項(xiàng),只需研究

對于(27),注意到

且y0在漸近分析中不起作用.因此根據(jù)(24)和Hansen[17]的Theorem 2.1,有

容易看出,(26)和(29)是聯(lián)合收斂的.對于(28),先定義

然后將證明隨機(jī)向量(28)依分布收斂于一個多元正態(tài)隨機(jī)向量,即

要證結(jié)論(31),根據(jù)Cram′er-Wold方法,只需證:對任意的非零q維常數(shù)列向量a=(a1,……,aq)T,

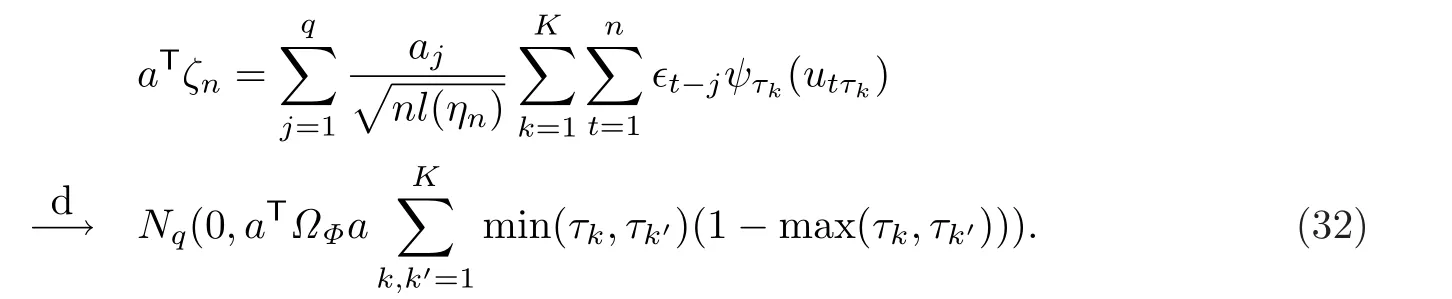
顯然,E(aTζn)=0.接下來,把a(bǔ)Tζn分解成兩部分:

不難知道等式(33)右邊的第二項(xiàng)相對于第一項(xiàng)是可忽略的.所以,只需證明等式(33)右邊的第一項(xiàng)有正態(tài)的極限分布.記

顯然mnt關(guān)于Ft是一個鞅差序列,且

在上式中利用了(30)中的定義.因此根據(jù)鞅中心極限定理,要證明(32)成立,只需驗(yàn)證下面的Lindeberg條件成立即可.對任意給定的δ ＞0,

接下來就來驗(yàn)證它.首先來證明

對任意的θ ＞0,利用Cs¨org?o等[12]中的Lemma 1,有

所以(35)成立.容易看出(35)可推出

進(jìn)一步地,注意到|ψτk(utτk)|≤2,有

這意味著

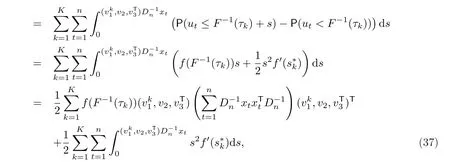
這意味著

結(jié)合(37),(39)和(40),可得

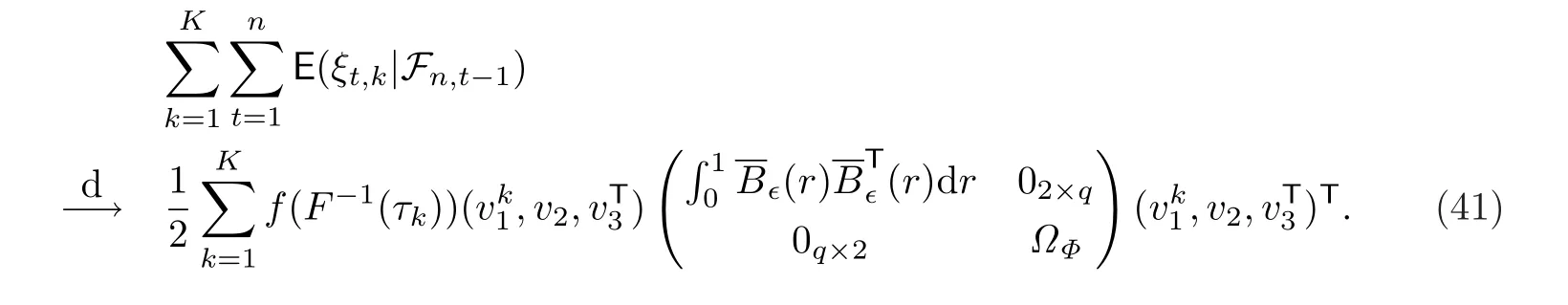
現(xiàn)在,結(jié)合(25),(26),(36),(41)和(42)(并注意到(26),(36),(41)和(42)是聯(lián)合收斂的),可得

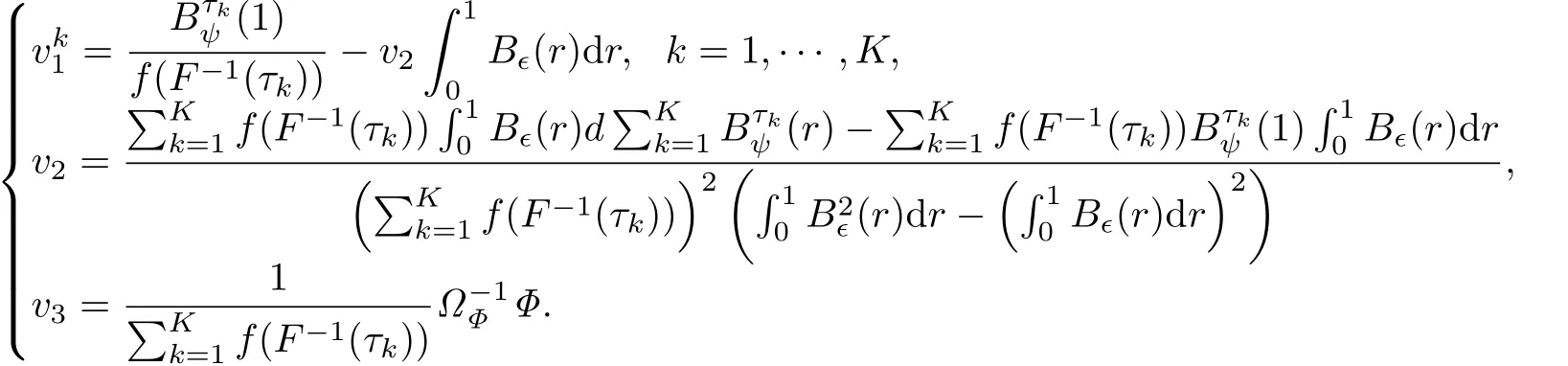
那么根據(jù)Knight[14]的Lemma A,可得