自旋-1角動量分量的不確定關(guān)系
南 華, 玄東平, 胡曉會
(延邊大學(xué) 理學(xué)院數(shù)學(xué)系, 吉林 延吉 133002)
1 引言與預(yù)備知識
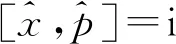
對于兩個(gè)可觀測量A和B, Robertson[4]推導(dǎo)出不等式

(1)
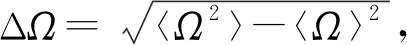
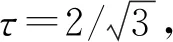
2 乘積形式的不確定關(guān)系
自旋角動量是量子系統(tǒng)的可觀測量, 已知自旋-1角動量的三個(gè)分量為
且滿足與軌道角動量相同的對易關(guān)系:
[Sx,Sy]=i?Sz, [Sy,Sz]=i?Sx, [Sz,Sx]=i?Sy.
(2)
令?=1, 由不確定關(guān)系(1)可得
ΔSxΔSy≥|〈Sz〉|/2, ΔSyΔSz≥|〈Sx〉|/2, ΔSzΔSx≥|〈Sy〉|/2,
(3)
因此, 有
(ΔSxΔSyΔSz)2≥|〈Sx〉〈Sy〉〈Sz〉|/8.
(4)
由于式(4)僅在不等式兩端全為0時(shí)等號成立, 但沒有實(shí)際意義.因此考慮不確定關(guān)系

(5)
使式(5)等號成立的τ稱為三方系數(shù), 其作用是使式(5)在兩端非零時(shí)可達(dá)到下確界, 即不確定關(guān)系(5)是緊的.
考慮系統(tǒng)純態(tài)的一般形式
通過計(jì)算可得
為確定不等式(5)中常數(shù)τ的值, 根據(jù)
對于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得
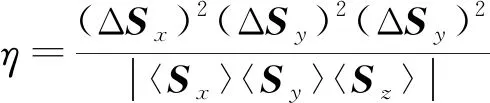
(6)
的最小值.可知當(dāng)θ1=π/2,θ2=5π/4時(shí), 存在π/5<α1<π/4, π/9<α2<π/8, 使得
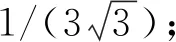
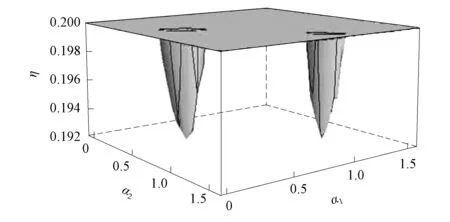
圖1 式(6)最小值的數(shù)值解Fig.1 Numerical solution of minimum value of formula (6)
3 和式的不確定關(guān)系
下面研究自旋-1角動量的三個(gè)分量相關(guān)和式的不確定性關(guān)系.由式(2)可得
(ΔSx)2+(ΔSy)2≥2ΔSxΔSy≥|〈Sz〉|,
(ΔSy)2+(ΔSz)2≥|〈Sx〉|, (ΔSx)2+(ΔSz)2≥|〈Sy〉|.
(7)
由式(7)可得三個(gè)分量的和式不等式
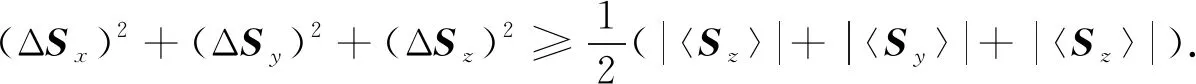
(8)
對于N維系統(tǒng), 自旋-l時(shí)自旋量子數(shù)l=(N-1)/2, 且對任意量子態(tài)有
由于Sk(k=x,y,z)的期望值定義了一個(gè)向量, 其最大長度等于沿任意軸的極值特征值, 因此文獻(xiàn)[16]給出了如下不等式
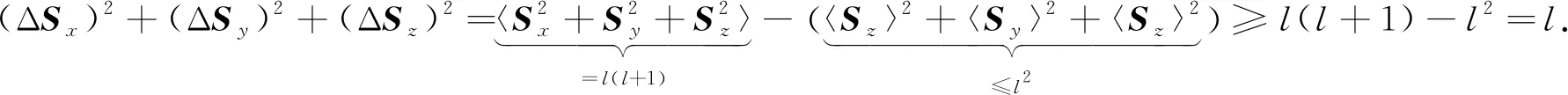
(9)
對一組數(shù)據(jù){x1,x2,…,xn}, 已知代數(shù)平均值不超過二次平均值, 即
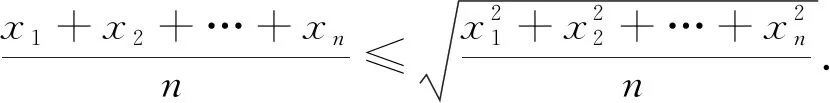
(10)
由此可得
由式(11)可知, 式(8)是非緊的, 因此考慮存在一個(gè)常數(shù)τ, 使不確定關(guān)系
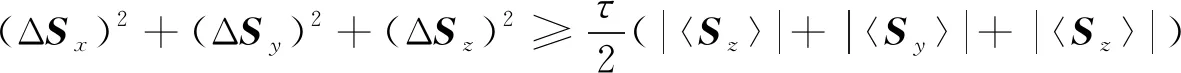
(12)
成為緊的, 即可達(dá)到該下確界.
對于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得
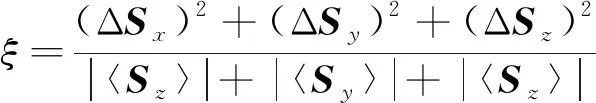
(13)
的最小值.
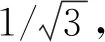
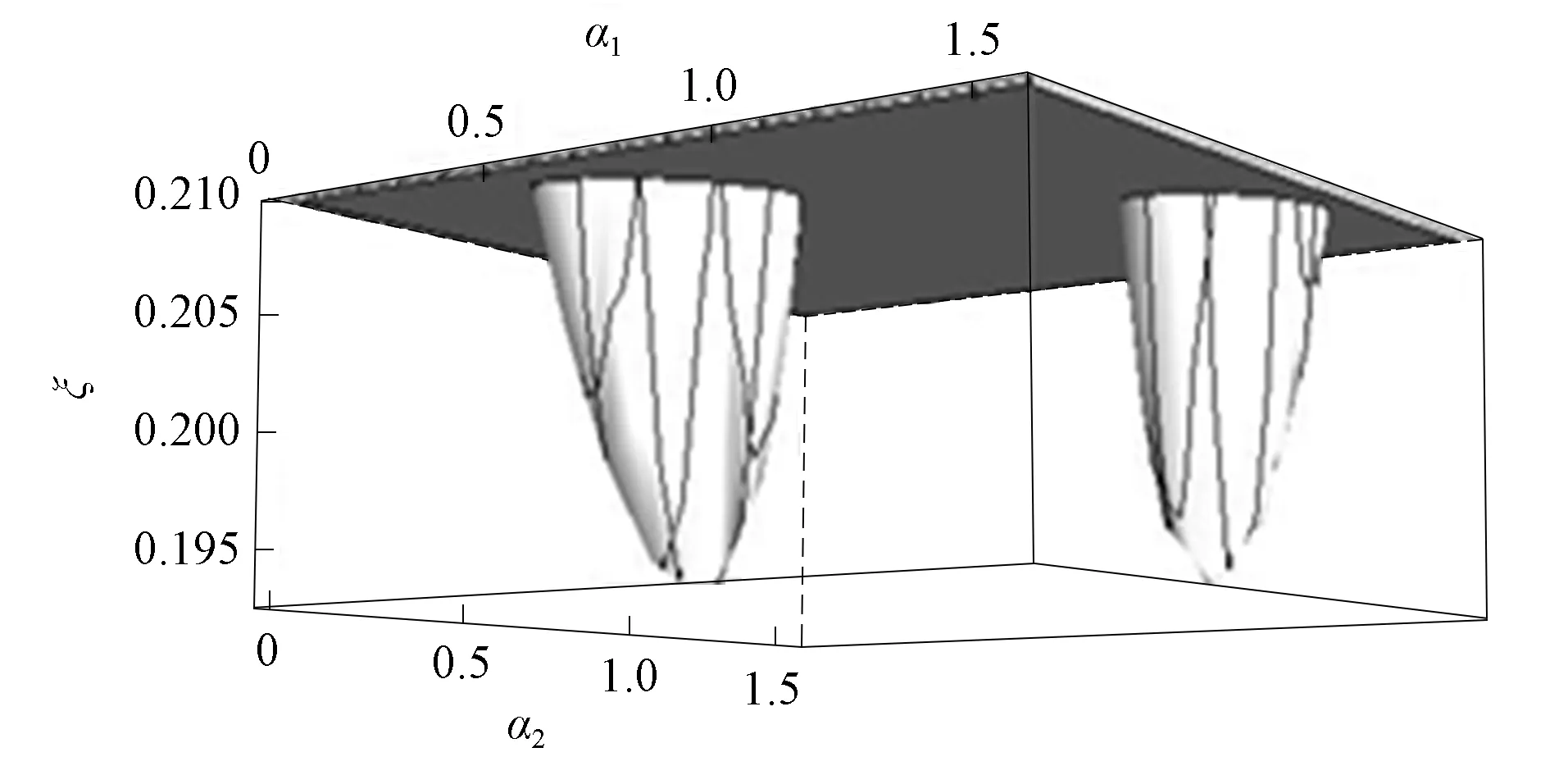
圖2 式(13)最小值的數(shù)值解Fig.2 Numerical solution of minimum value of formula (13)
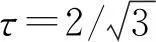
 吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年4期
吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年4期
- 吉林大學(xué)學(xué)報(bào)(理學(xué)版)的其它文章
- Exendin-4螺旋結(jié)構(gòu)對生物活性及穩(wěn)定性的影響
- 由氮雜環(huán)配體控制結(jié)構(gòu)的從三維骨架到二維層的Mn(Ⅱ)配位聚合物
- 高分子鏈模型對兩親性二嵌段共聚物系統(tǒng)均勻溶液/膠束轉(zhuǎn)變的影響
- 一個(gè)參數(shù)未知的網(wǎng)格多渦卷超混沌系統(tǒng)的自適應(yīng)同步
- 基于混沌遺傳算法的無線傳感器網(wǎng)絡(luò)改進(jìn)LEACH算法
- 半監(jiān)督技術(shù)和主動學(xué)習(xí)相結(jié)合的網(wǎng)絡(luò)入侵檢測方法
