探究圓錐曲線關(guān)于切線長的統(tǒng)一恒等式

廣東省中山市桂山中學(xué)(528463) 譚天眾

1 背景

文[1]給出以下結(jié)論:

性質(zhì)1已知O為坐標(biāo)原點,點T(x0,y0)為圓錐曲線C上一點,C在點T處的切線為l,點P是l上的任意一點(和點T不重合),過點P作OT的平行線交圓錐曲線于不同的兩點A,B,則λ=為定值.

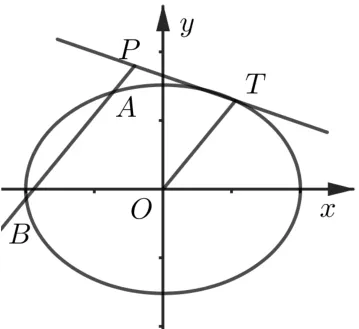
圖1

文[2]給出以下結(jié)論:

性質(zhì)2 (1)如圖2,已知點P在橢圓C:=1上,點Q(m,n)不在橢圓C上,過點Q作平行于OP的直線

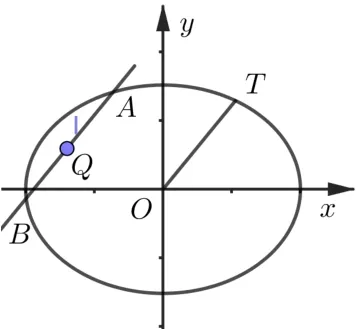
圖2

我們發(fā)現(xiàn)兩個結(jié)論之間有聯(lián)系,并思考能否將兩個結(jié)論結(jié)合起來得到更優(yōu)美的結(jié)論呢?

2 探究與結(jié)論

證明已知O為坐標(biāo)原點,點T(x0,y0)為橢圓C上一點,C在點T處的切線為l,點P(xp,yp)是l上的任意一點(和點T不重合),過點P作OT的平行線交橢圓于不同的兩點A,B,則由性質(zhì)1(1)得到,

與橢圓的情形類似,我們可以得到雙曲線的如下等式,因其證明與橢圓的情形相似,不再贅述.

再研究拋物線y2=2px的情形.

引理2 已知T(x0,y0)是拋物線C:y2=2px上的非頂點的點,點P(xp,yp)不在拋物線C上,過點P作平行于OT的直線拋物線C于A,B兩點,則

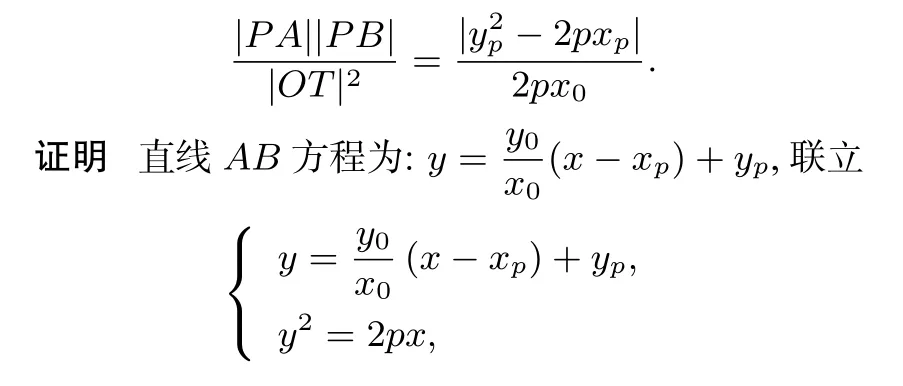
恒等式3 過點P(xp,yp)作拋物線y2=2px的兩條切線,T,Q的兩分別為切點,F為拋物線的焦點,則

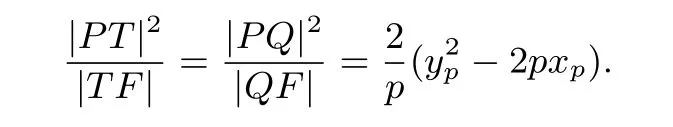
證明設(shè)O為坐標(biāo)原點,點T(x0,y0)(非原點)為拋物線C上一點,C在點T處的切線為l,點P(xP,yP)是l上的任意一點(和點T不重合),過點P作OT的平行線交拋物線于不同的兩點A,B,由性質(zhì)1(3)得到

以上三個恒等式如果用語言表述,可以表述為“過圓錐曲線外一點作圓錐曲線的兩條切線,則切線長平方與切點的焦半徑的乘積之比相等”,統(tǒng)一簡潔優(yōu)美.