廣義Mycielski圖的鄰和可區(qū)別全染色
白 羽,強(qiáng)會(huì)英
(蘭州交通大學(xué) 數(shù)理學(xué)院,甘肅 蘭州 730070)
0 引言
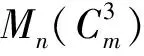
1 預(yù)備知識(shí)
定義1[2]對(duì)簡(jiǎn)單圖G,存在映射f:V(G)∪E(G)→{1,2,…,k},若同時(shí)滿足:
1) ?uv∈E(G),f(u)≠f(v);
2) ?uv,vw∈E(G)且u≠w,f(uv)≠f(vw);
3) ?uv∈E(G),f(u)≠f(uv),f(v)≠f(uv);


定義2[3]設(shè)G是m階簡(jiǎn)單圖,V(G)={v01,v02,…,v0m},m,n∈N+,圖G的Mycielski圖Mn(G)是指
1)V(Mn(G))={v01,v02,…,v0m;v11,v12,…,v1m;…;vn1,vn2,…,vnm};
2)E(Mn(G))=E(G)∪{vijv(i+1)k|v0jv0k∈E(G),1≤i≤n,1≤j≤m}.
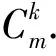
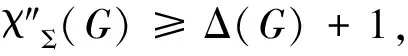
2 主要結(jié)論
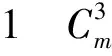

情形1 當(dāng)m≡0(mod5)時(shí),(0≤i≤n,1≤j≤m),令f為
f(v01v0m)=7,f(v01v0,m-2)=4,f(v02v0,m-1)=5,f(v03v0m)=1.
其余邊染法如下:
當(dāng)i≡0(mod2)時(shí),
f(vi1vi+1,m)=f(vimvi+1,1)=9,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=5,
f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=1,f(vi3vi+1,m)=f(vimvi+1,3)=2.
當(dāng)i≡1(mod2)時(shí),
f(vi1vi+1,m)=f(vimvi+1,1)=7,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=4,
f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=5,f(vi3vi+1,m)=f(vimvi+1,3)=1.

表1 當(dāng)m≡0(mod5)時(shí),S(vij)和的情況
情形2 當(dāng)m≠0(mod5)時(shí),(0≤i≤n,1≤j≤m),令f為
其中p 情形2.1m≡1(mod5)時(shí), f(v01v0,m-2)=5,f(v02v0,m-1)=f(v03v0m)=1,f(v01v0m)=9. 其余邊染法如下. 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,m)=f(vimvi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=10, f(vi3vi+1,m)=f(vimvi+1,3)=2,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=7,f(vi1vi+1,2)=f(vi2vi+1,1)=8. 當(dāng)i≡1(mod2)時(shí), f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=1, f(vi1vi+1,m)=f(vimvi+1,1)=9,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=5. 表2 當(dāng)m≡1(mod5)時(shí),S(vij)和的情況 情形2.2m≡2(mod5)時(shí),令f為 f(v01v0,m-2)=8,f(v02v0,m-1)=9,f(v03v0m)=2, f(v0,m-2v0,m-1)=1,f(v0,m-1v0m)=3,f(v01v0m)=4. 其余邊染法如下. 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,2)=f(vi2vi+1,1)=5,f(vi2vi+1,3)=f(vi3vi+1,2)=1, f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)= f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=10,f(vi1vi+1,m)=f(vimvi+1,1)=9, f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=2,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=8. 當(dāng)i≡1(mod2)時(shí), f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=9,f(vi3vi+1,m)=f(vimvi+1,3)=2, f(vi1vi+1,m)=f(vimvi+1,1)=4,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=8, f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=1,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=3. 表3 當(dāng)m≡2(mod5)時(shí),S(vij)和的情況 情形2.3m≡3(mod5)時(shí),令f為 f(v01v0,m-2)=f(v02v0,m-1)=f(v03v0m)=9,f(v0,m-2v0,m-1)=2,f(v0,m-1v0m)=4,f(v01v0m)=5. 其余邊染法如下. 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,2)=f(vi2vi+1,1)=8,f(vi2vi+1,3)=f(vi3vi+1,2)=1, f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=10, f(vi1vi+1,m)=f(vimvi+1,1)=7,f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=3,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=6. 當(dāng)i≡1(mod2)時(shí), f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=9, f(vi1vi+1,m)=f(vimvi+1,1)=5,f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=2,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=4. 表4 當(dāng)m≡3(mod5)時(shí),S(vij)和的情況 情形2.4m≡4(mod5)時(shí),令f為 f(v01v0,m-2)=f(v02v0,m-1)=f(v03v0m)=6,f(v01v02)=5, f(v0,m-2v0,m-1)=f(v01v0m)=4,f(v0,m-,3v0,m-2)=f(v0,m-1v0m)=3. 其余邊染法如下. 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,m)=f(vimvi+1,1)=f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=10, f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=8,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=5, f(vi,m-3vi+1,m-2)=f(vi,m-2vi+1,m-3)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=9, f(vi2vi+1,3)=f(vi3vi+1,2)=1,f(vi1vi+1,2)=f(vi2vi+1,1)=f(vi3vi+1,m)=f(vimvi+1,3)=7. 當(dāng)i≡1(mod2)時(shí), f(vi,m-3vi+1,m-2)=f(vi,m-2vi+1,m-3)=f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=3, f(vi1vi+1,2)=f(vi2vi+1,1)=5,f(vi1vi+1,m)=f(vimvi+1,1)=f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=4, f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=6. 表5 當(dāng)m≡4(mod5)時(shí),S(vij)和的情況 情形1 當(dāng)k≡1(mod2)時(shí),(0≤i≤n,1≤j≤2k). f(v0jv0,j+k)=3,f(v01v0,2k)=7, 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,2k)=f(vi,2kvi+1,1)=8, f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=4, 當(dāng)i≡1(mod2)時(shí), f(vi1vi+1,2k)=f(vi,2kvi+1,1)=7, f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=3, 情形2 當(dāng)k≡0(mod2)時(shí),(0≤i≤n,1≤j≤2k). 令f為f(vik)=1,f(vi,k-1)=f(vi,2k)=3. 當(dāng)i≡0(mod2)時(shí), f(vi1vi+1,2k)=f(vi,2kvi+1,1)=8, f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=4, 當(dāng)i≡1(mod2)時(shí), f(vi1vi+1,2k)=f(vi,2kvi+1,1)=7, 表6 當(dāng)k≡0(mod2)時(shí),S(vij)和的情況



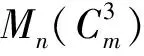


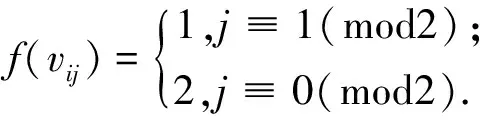
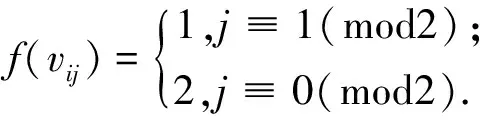


 淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)2023年3期
淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)2023年3期
- 淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)的其它文章
- 課程游戲化背景下幼小銜接的現(xiàn)實(shí)困境與突破路向
- 學(xué)科建設(shè)視閾下法治人才培養(yǎng)的機(jī)制創(chuàng)新研究
- 新文科背景下“中國(guó)園林史”課程的美育教學(xué)模式改革
- 大數(shù)據(jù)技術(shù)賦能高校思想政治理論課教學(xué)評(píng)價(jià)的三維向度
- 《新課標(biāo)》下英語(yǔ)學(xué)科教學(xué)的后現(xiàn)代主義轉(zhuǎn)向及其路徑探究
- 智媒時(shí)代新聞傳播人才高質(zhì)量培養(yǎng)的現(xiàn)實(shí)困境與實(shí)踐路徑
