The(1+1)-dimensional nonlinear ion acoustic waves in multicomponent plasma containing kappa electrons
Mai-Mai Lin(林麥麥), Lei Jiang(蔣蕾), and Ming-Yue Wang(王明月)
College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China
Keywords: multicomponent plasma,nonlinear ion acoustic waves,Sagdeev potential method
1.Introduction
Recently,the nonlinear waves in multicomponent plasma have been investigated in various fields of physics,such as the laboratory plasma, the earth atmosphere space plasma exploration and others.[1-5]Owing to the balance between nonlinearity and dissipation,a dissipative effect leading to the formation of nonlinear structures is created.The study of nonlinear waves in complex plasmas has become one of the hot topics in plasma physics.[6]Ion acoustic wave has become one of the most important aspects of nonlinear phenomena in plasma physics.Since Nakamua studied the ion plasma physics,[6]ion acoustic wave has become one of the most important aspects of nonlinear phenomena in plasma physics.Since Nakamua studied the ion acoustic solitary wave in multicomponent plasma, many scholars have done a lot of theoretical researches on this topic.[7]The propagation of arbitrary amplitude ion acoustic solitary wave in a two-component plasma has been investigated by using an alternative model.[8]The behavior of particle distribution in complex plasma is usually described by kappa distribution.[9]The diffusion of particles with kappa-distributed velocities is strongly influenced by statistical correlations.[10]A lot of observations have shown that ultra-hot particles with non-Maxwell distribution in the form of power law exist widely in space plasma.The plasma systems with superthermal electrons are well described by the kappa distribution.[11]It is necessary to point out that the Sagdeev potential method plays an important role in studying nonlinear waves.[12]Meanwhile, the propagation of nonlinear dust ion acoustic wave(DIAW)in unmagnetized collisionless dusty plasma consisting of ions,nonthermal electrons,and negatively charged dust grains has been investigated by using the Sagdeev potential method.[13]In a collisionless magnetized plasma in the presence of negative ions, the solitary kinetic Alfven wave has been theoretically investigated by the Sagdeev potential approach.[14]
In this paper, the large amplitude nonlinear ion acoustic waves in a multicomponent plasma composed of positively charged ions, negative ions, ion beam, and kappa-distributed electrons are investigated by the Sagdeev potential method.The rest of this paper is organized as follows: In Section 2,the basic equations of theoretical model are presented.Meanwhile, the Sagdeev potential equation is obtained.In Section 3,the effects of different parameters on the phase diagramare discussed.In Section 4,the variations of the Sagdeev potential function and the characters of solitary waves are studied in detail.In Section 5, the main conclusions are drawn from the present study.
2.Basic equations
In order to study the nonlinear ion acoustic wave in a multicomponent plasma, we assume that a collisionless and unmagnetized plasma consists of five components: positively charged ions,negatively charged ions,ion beam,kappadistributed electrons,and dust particles.[15]The dimensionless equations are as follows:
whereni+,ni-,andnbdenote the dimensionless number density of positively charged ions, negatively charged ions, and ion beam, which are normalized by their equilibrium valuesni+0,ni-0,nb0, respectively,ui+,ui-,ubdenote the velocity of positive ions, velocity of negative ions, and velocity of ion beam,which are normalized by the positively charged ion sound velocityCS=(kBTe/mi+),withkBbeing the Boltzmann constant,Tethe temperature of electrons andmi+the mass of positive ions.The potentialφis normalized bykBTe/e,whereeis the number of electronic charges.The parameters in this system are as follows:α=mi+/mi-,β=mi+/mb,μd=Zdnd0/ne0,μi+=ni+0/ne0,μi-=ni-0/ne0,andμb=nb0/ne0,wheremi-is the mass of negative ion andmbis the mass of ion beam,Zdis the charge number of dust grain,nd0is the equilibrium number density of dust grains andne0is the equilibrium number density of electrons.The kappa distribution of electrons is
whereκis the kappa number of electrons.
The plane-wave solutions for the particle number density,particle propagation velocity, and electric potential have the following form:
The linear wave dispersion relation can be expressed as
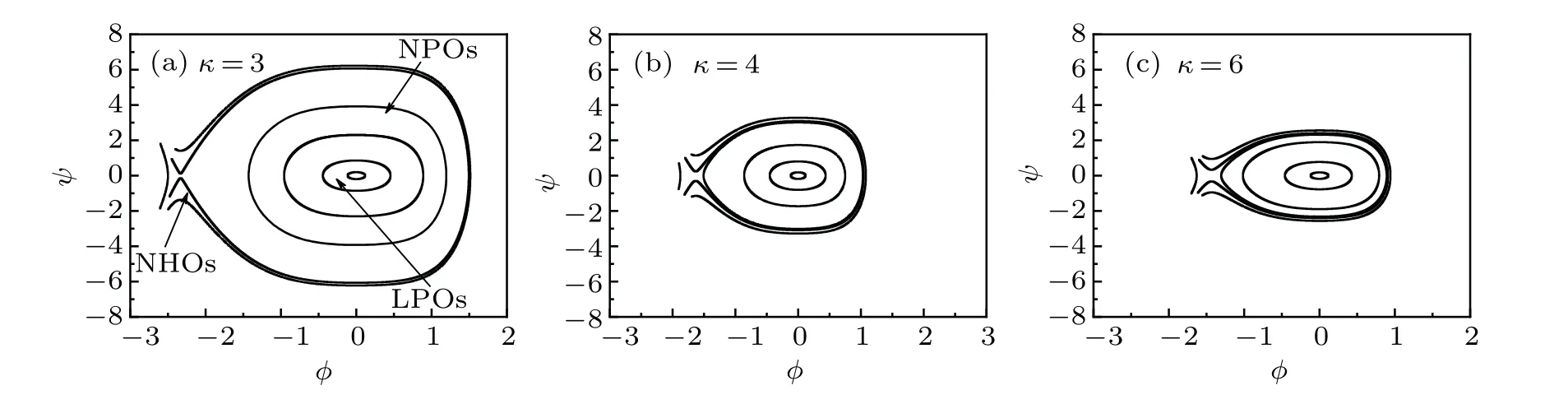
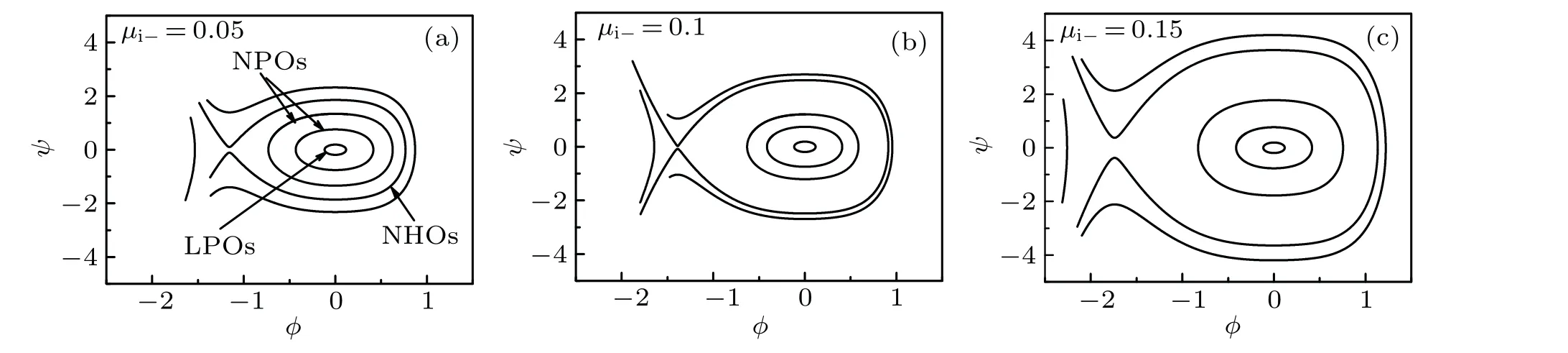
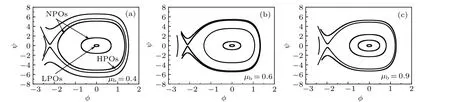
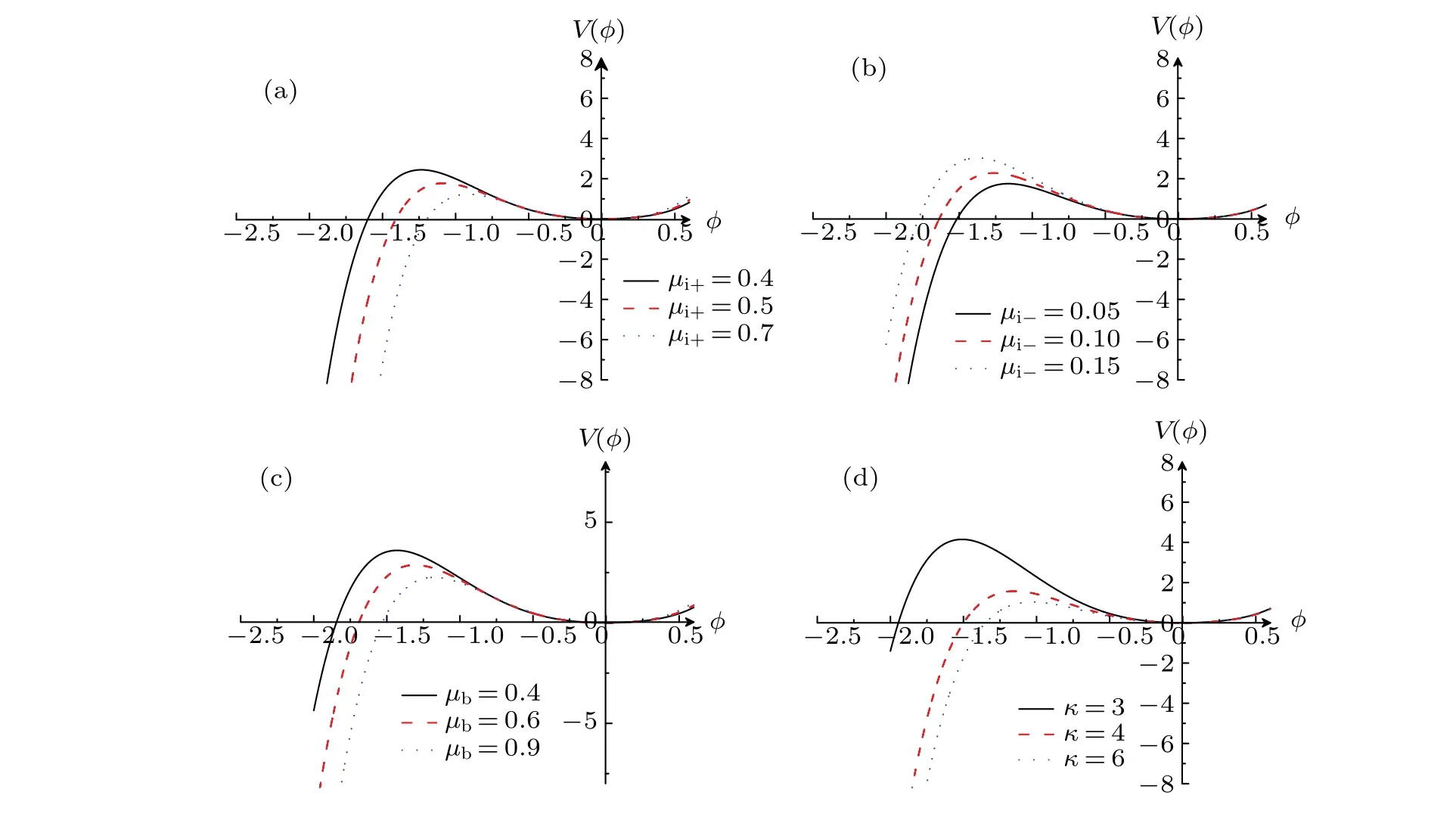
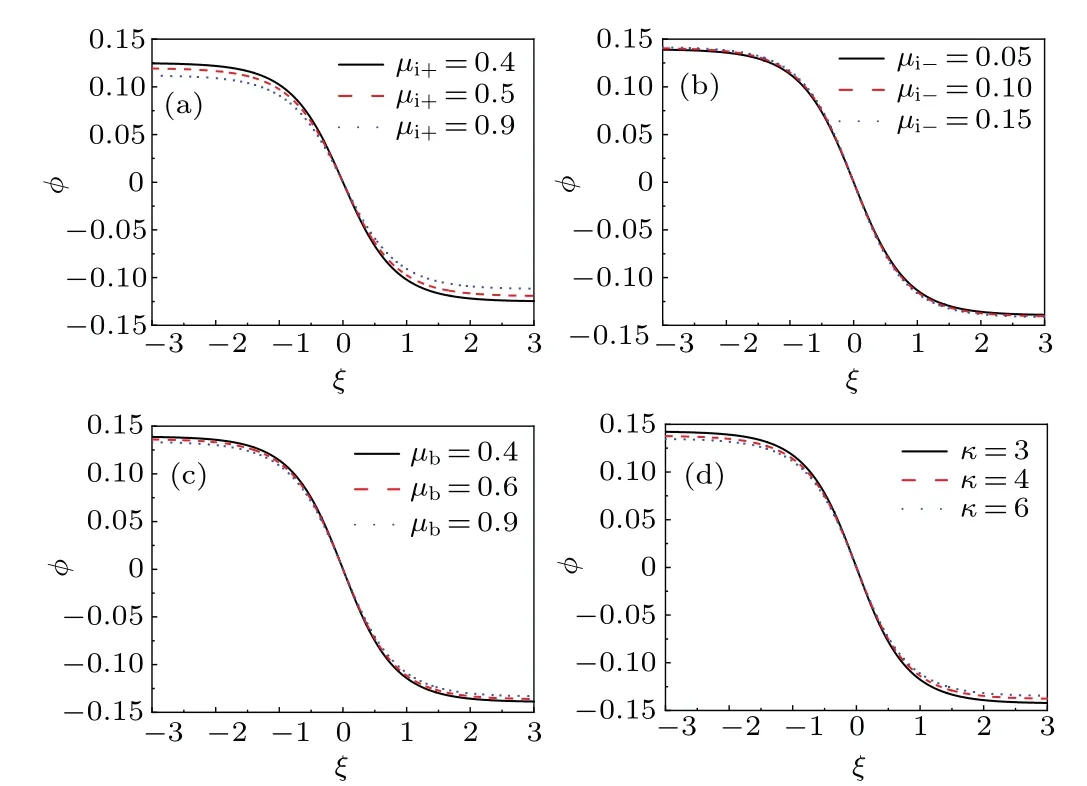
Figure 1 shows the influence of wave numberkon the dispersion relation for linear equation for different values ofμi+,μi-,μb,andκ,indicating that when 0 Fig.1.Characteristics of dispersion relation at α =1 and β =0.7,and various values of(a)-(c)μi+,μi-,andμb and(d)κ,respectively. To investigate the ion acoustic waves in the multicomponent plasma system, the Sagdeev potential method is used to solve Eqs.(1)-(7).Now, a new coordinateξis introduced, which is given byξ=x-Mt, whereMis the Mach number.Then, The following boundary conditions should be noted: whenξ →±∞, the dimensionless number densityni+,i-,b→1,the dimensionless velocityui+,i-,b→0,and the potentialφ →0. With the help of Sagdeev potential method, the number densities can be obtained as shown below: Meanwhile, the Sagdeev potential equation can be expressed as At the same time,an analytical soliton solution for ion acoustic nonlinear shock wave in this system can be given as follows: In order to investigate the different types of waves in the multicomponent plasma with kappa-distributed electrons, the various effects of different values of parametersκ,μi+,μi-,andμbare analyzed and the results are plotted in Figs.2-5. Fig.2.Variations of phase diagram with φ for three different values of κ. Figure 2 shows the variations of phase diagram withφfor kappa numberκ=3, 4, and 6, and atα=1,β=0.7,μi+= 0.4,μi-= 0.2, andμb= 0.2.[18,19]It is shown that three kinds of orbits coexist in the multicomponent plasma system,which have the linear periodic orbits(LPOs),the nonlinear periodic orbits(NPOs)and the nonlinear homoclinic orbits(NHOs).It means that the linear periodic wave solution,the nonlinear periodic wave solution and the solitary wave solution are coexistent in this multicomponent plasma.Meanwhile, it is found from Fig.2 that the variation of the kappa number in the complex plasma system also affects the existence range of different types of orbits in this dynamical system. Figures 3-5 show the influence ofμi+,μi-,andμbon the phase diagram for this dynamical system.As is well known,the parameters in the multicomponent plasma are expressed asμi+=ni+0/ne0,μi-=ni-0/ne0,andμb=nb0/ne0,indicating that for the multicomponent plasma with kappa-distributed electron, the various values of the equilibrium number densities for positive ions,negative ions,ion beam,and electrons in this system will change the existence ranges of different types in the phase diagram for this system.However,the linear periodic wave solution,the nonlinear periodic wave solution and the solitary waves solution are all coexistent in this system. Fig.4.Variations of phase with φ for three different values ofμi- at κ =3,μi+=0.4,andμb=0.2. Fig.5.Variations of phase with φ for different values ofμb at κ =3,μi+=0.4,andμi-=0.2. In order to discuss the behaviors of the nonlinear ion acoustic solitary waves,the characteristics of the Sagdeev potentialV(φ)versusφwith various parameters is investigated in Fig.6 by the numeral simulation method.Figure 6(a)shows that there existsφmon the Sagdeev potential curves, whereV(φm)=0.It can also be found thatφm<0 whenμi+=0.4,0.5, 0.7, respectively.It indicates that there exist only rarefactive solitary waves in the multicomponent plasma.In additional, figure 6(a) also indicates that the amplitude of ion acoustic solitary wave will decrease as the value ofμi+increases.Because of the parameterμi+=ni+0/ne0, it can be concluded that the amplitude of rarefactive solitary waves will decrease with equilibrium number density of positive ions increasing and equilibrium number density of electrons lowering.It means that both the equilibrium number density of positive ions and the equilibrium number density of electrons can have considerable influence on the solitary wave.Figure 6(b)shows the influence ofμi-on the Sagdeev potentialV(φ)and only the rarefactive solitary wave existing in this system.Becauseμi-=ni-0/ne0, the amplitude of solitary wave will increase if the multicomponent plasma has a higher equilibrium number density of negative ions.Figure 6(c) shows the variations ofV(φ) versusφfor three different values ofμb.It is shown that the influences ofμbon the characteristics of solitary wave are similar to those in Fig.6(a).The variations ofV(φ) versusφwith different values ofκare plotted in Fig.6(d).It is found that the amplitude of solitary wave decreases with the augment of the kappa number of kappadistributed electrons in the multicomponent plasma.As stated above, it can be concluded that the variations ofV(φ)versusφcan be influenced by many parameters of multicomponent plasma. In order to study the characteristics of the ion acoustic solitary waves, the variations of solitary wave described by Eq.(24) are plotted in Fig.7 through the numerical simulation technique.Figure 7 shows that there exist only rarefactive solitary waves in the multicomponent plasma with kappadistributed electrons,and that the amplitude of rarefactive solitary wave decreases asμi+,μb, andκincrease, but increases asμi-increases.This conclusion is consistent with that from Fig.6.It is found that the effects of different parameters on the ion acoustic solitary waves are very important. Fig.6.Variations of Sagdeev potential V(φ)with φ at α =0.8 and β =0.7. Fig.7.Characteristics of φ versus ξ of solitary waves for three different values of(a)-(c)μi+,μi-,andμb and(d)κ,at α =1 and β =0.7. The propagating process of the shock wave is the same as that of sound waves, which is characterized by the heteroclinic orbits in a two-dimensional dynamical system.In some plasma studies, the electrostatic energy of the dust particles may affect the shock wave through its energy conversion.[20]The different values of Mach number can also affect the width of shock wave.[21] In order to study the characteristics of ion acoustic nonlinear shock wave, the variations of shock wave in Eq.(25)are plotted in Fig.8 by the numerical simulation technique.Figure 8 shows that there exist shock waves in the multicomponent plasma with kappa-distributed electrons.Moreover, it is shown that the amplitude of the nonlinear shock wave decreases asμi+,μb, andκincrease, but increases asμi-increases.It is found that the effects of kappa distribution properties and particle number density on the shock waves are also very important. Fig.8.Characteristics of φ versus ξ of shock waves for three different values of(a)-(c)μi+,μi-,μb and(d)κ,at α =1 and β =0.7. In this paper, the characteristics of large amplitude nonlinear ion acoustic solitary wave in collisionless, unmagnetized multicomponent plasma with kappa-distributed electrons are investigated by the Sagdeev potential method.It is found from the phase diagram for the dynamical system that the linear periodic orbits,the nonlinear periodic orbits,and the nonlinear homoclinic orbits are all exist in this system.Moreover,it can be concluded from the different values ofV(φ)that only the rarefactive solitary wave exists, and different parameters exert important influence on the characteristics of ion acoustic solitary wave and ion acoustic nonlinear shock wave.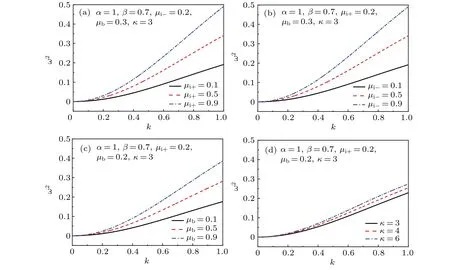


3.Analysis of dynamical system
4.Discussion

5.Conclusions
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures

