孔慧華,潘晉孝

(中北大學 理學院,山西 太原 030051)

圖像重建算法主要分為兩大類,一類是濾波反投影算法,以傅里葉切片定理為基礎(chǔ),能夠用快速傅里葉變換,既快速又可信;然而,濾波反投影要求數(shù)據(jù)是完全的,受噪聲影響也較大.另一類是迭代重建算法,它適合于各種幾何學并允許從不完全投影數(shù)據(jù)和噪聲投影數(shù)據(jù)重建,能夠減少金屬偽像,更好地處理有限角度的斷層成像.常用的迭代算法有 ART[1],SART[2],Cimmino’s method[3],DWE和CAV[4-5]等.但由于迭代算法重建速度慢,嚴重限制了它的使用.1994年,Hudson等提出了有序子集算法(Ordered Subsets,OS)[6],大大減少了重建時間,加快了迭代重建的速度.雖然增加子集的數(shù)目可以加速迭代收斂,然而子集個數(shù)太多會由于子集內(nèi)缺少統(tǒng)計信息而導(dǎo)致圖像質(zhì)量下降[7].本文提出了一種基于統(tǒng)計理論的子集劃分方法,既能夠加速收斂又能保證每個子集內(nèi)含有充分的統(tǒng)計信息.

1 背景知識

代數(shù)重建算法是將連續(xù)的圖像離散化,從而轉(zhuǎn)化成代數(shù)方程組

的求解問題.其中,R=(rij)I×J為系統(tǒng)矩陣(通常是一個大型非負稀疏矩陣);y=(y1,y2,…,yl)T為測量投影;x=(x1,x2,…,xJ)T為未知圖像向量.圖像重建問題就是從測量投影 y重建未知圖像 x.由于系統(tǒng)矩陣的病態(tài)性,測量數(shù)據(jù) y的噪聲污染性以及在實際應(yīng)用中數(shù)據(jù)的巨大維數(shù),對該問題直接求解顯然是不可行的.而迭代算法由于在上述問題中的優(yōu)越性,被發(fā)展成了有效的圖像重建算法.

解方程 (1)的大部分迭代算法可以被寫為下面的形式[8]

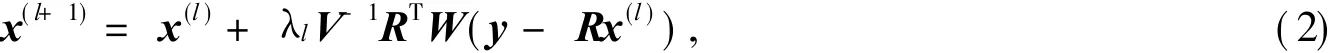
式中:V和W分別是兩個正定對角矩陣,階數(shù)分別為 J,I;λl是松弛因子.由于迭代系統(tǒng) (2)在每次更新像素值時用到了觀測數(shù)據(jù) y中的所有元素,從而被稱為是聯(lián)合的.

近年來,式 (2)的 OS形式引起了人們的很大興趣.設(shè)指數(shù)集合 B={1,2,… ,I}可以被分成 T個非空的不相重疊的子集

假設(shè)

設(shè)

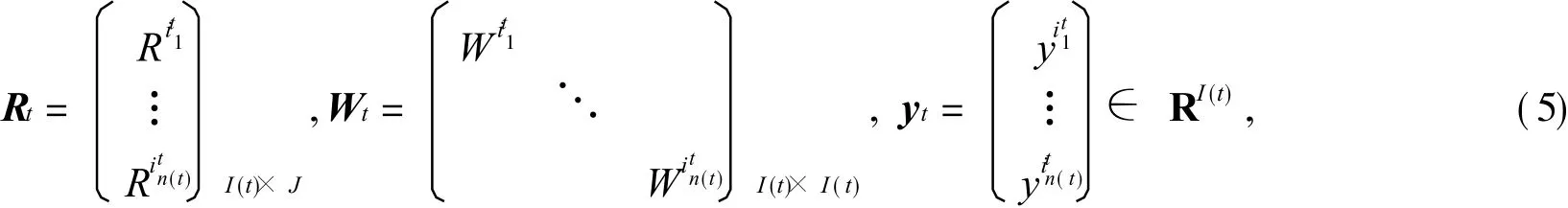
式中:Ri是 R的第 i行;Wi是 W的第 i行對角線元素;yi是 y的第 i行元素.則式 (2)的 OS形式可以被寫作[8]

其中:[l]=l(mod T)+1對 l≥T.從 l=k T到 l=(k+ 1)T(k=0,1,2,L)的迭代過程叫做一個 OS循環(huán),一個循環(huán)內(nèi)所有的子集恰好被用到一次.當 T=1時,式 (6)還原為聯(lián)合形式 (2).

通過合適地選擇對角矩陣 V和 W,算法 SART,Cimmino’s,DWE,CAV都能夠被寫成式(2)或者式(6)的形式[8].

2 統(tǒng)計自適應(yīng)子集算法

在使用 OS算法時,保證子集內(nèi)有充分的統(tǒng)計信息是非常重要的,一般子集的形成要避免對噪聲敏感或其它偽跡的形成.傳統(tǒng)的 OS算法中,通常選取的子集個數(shù) T是固定的,即每個子集內(nèi)含有相同的投影數(shù).本文提出的統(tǒng)計自適應(yīng)子集利用統(tǒng)計學中的假設(shè)檢驗[9]方法來劃分子集.首先,提出假設(shè),建立檢驗統(tǒng)計量;然后根據(jù)給定的顯著性水平T求出 H0成立時的拒絕域;最后根據(jù)樣本觀測值進行判斷子集是否形成.

Ⅰ.提出假設(shè)

H0:子集內(nèi)統(tǒng)計信息達到用戶的要求?H 1:子集內(nèi)的統(tǒng)計信息還沒有達到用戶的要求.

Ⅱ.建立檢驗統(tǒng)計量

本文研究兩個劃分子集的檢驗統(tǒng)計量.第一個是對測量投影數(shù)據(jù) yi與估計投影數(shù)據(jù) y^i的差的平均值

式中:St,j表示像素 j的第 t個子集;m是子集 St,j內(nèi)穿過像素 j的投影數(shù)目.這個統(tǒng)計量反映了投影數(shù)據(jù)的一定信息量,但由于它分布中的參數(shù)不容易確定,在使用這個統(tǒng)計量時,通常是對這個量給定一個閾值,滿足接受,不滿足則拒絕.

第二個檢驗統(tǒng)計量的定義為

以定理的形式給出該統(tǒng)計量分布.

定理 1 如果圖像被認為是一個可行性圖像,即統(tǒng)計假設(shè) y1,y2,…,yl分別是均值為 y^1,^y2,… ,y^l的泊松采樣,能夠被接受[10].則

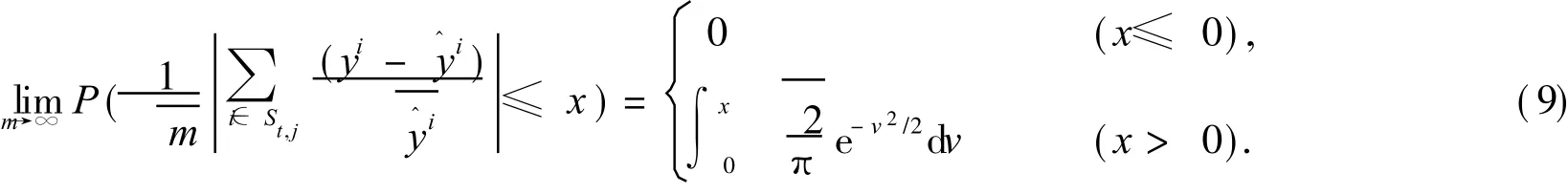
式中:St,j表示像素 j的第 t個子集;m是子集 St,j內(nèi)穿過像素 j的投影數(shù)目.

證明 由于圖像是可行性圖像,從統(tǒng)計上可以得到

于是

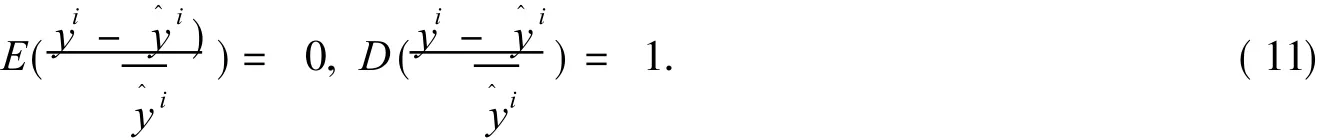
又由于從不同的探測器測得的數(shù)據(jù)是相互獨立的,根據(jù)中心極限定理可得結(jié)論.證畢.

由該定理可以看出,當 m充分大時,第二個統(tǒng)計量服從標準正態(tài)分布.

Ⅲ.根據(jù)樣本值進行檢驗

這里的檢驗是在重建過程中進行的,其步驟如下:①初始化圖像 x(0).②計算第 i根射線的投影值.③計算經(jīng)過第 i根射線的每個像素 j的統(tǒng)計量的值,并判斷是否落在拒絕域內(nèi).若檢驗通過,則接受假設(shè),像素 j的子集 St,j形成,對目前的 x j更新;否則拒絕假設(shè),子集不形成,像素值不被更新.④重復(fù)步驟②,③直到 I個方程都完成,這時得到的各 x j值叫做完成了第一輪迭代.一般要經(jīng)過 K輪迭代,直到取得符合收斂要求的結(jié)果為止.

設(shè) l=T(1)+ T(2)+…+T(n)+tn-1,其中 tn+1是第 n+1次迭代的第 t個子集,則該算法的迭代公式為

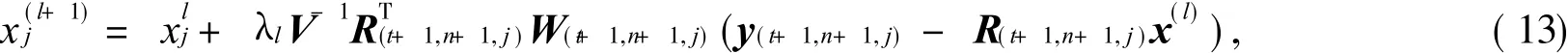
與有序子集的迭代公式非常相似.其中,Vj為矩陣 V第 j行對角線上的元素;(t+1,n+1,j)表示第 n+1次迭代第 j個元素的第 t+1個子集.

3 實驗結(jié)果與分析

實驗中,將統(tǒng)計自適應(yīng)子集 (Statistical Adaptive Ordered Subsets,SAOS)方法應(yīng)用在 SART上,得到 SAOS-SART.本文將將采用第一個檢驗統(tǒng)計量的 SAOS-SART表示為 SAOS-SART-A,用第二個檢驗統(tǒng)計量的 SAOS-SART表示為 SAOS-SART-B.重建公式如下

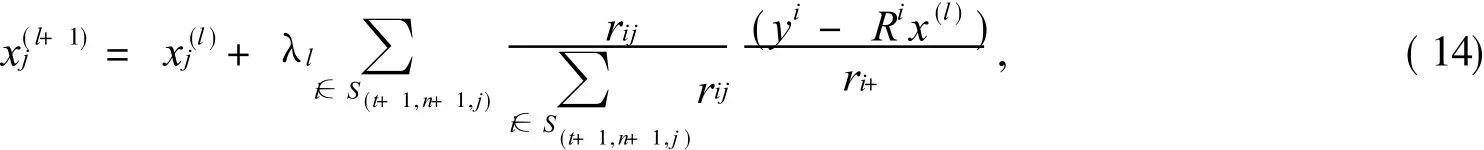
式中:x(jl+1)是像素 j對當前子集 t+ 1的更新值;x(jl)是像素 j更新前的值.

該公式只是對 OS-SART[11]的重建公式進行了很小的改動.

為了檢驗統(tǒng)計自適應(yīng)子集算法的可執(zhí)行性,將 OS-SART,SAOS-SART-A和 SAOS-SART-B的公式用 C語言在計算機 (RAM:1 G;CPU:P1.86 GHz)上進行編碼.

重建的收斂率用歸一化判據(jù) d衡量

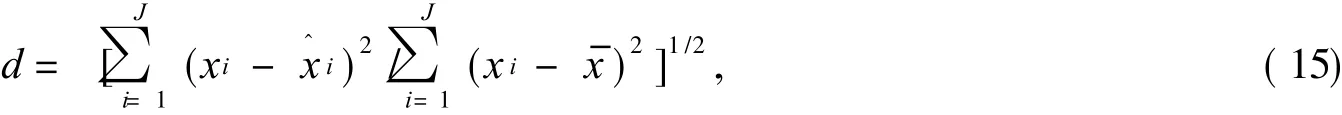
式中:xi和 x^i分別表示原圖像和重建圖像中第 i個像素的灰度;表示原始圖像的平均灰度.歸一化均方距離判據(jù)越小,表明重建圖像與原始圖像越接近,重建圖像的質(zhì)量越好.

實驗選取 Shepp-Logan切片作為仿真對象,大小為 256×256像素,灰度級為 0～ 255.投影采樣間隔為 1°,采樣區(qū)域為0°～ 180°.每個投影方向有 256個探測器.實驗中分別用無噪聲投影數(shù)據(jù)和加了投影總數(shù) 5%的泊松噪聲的投影數(shù)據(jù)進行重建.實驗中的參數(shù)設(shè)置如下:OS-SART的子集數(shù)為 45,SAOSSART-A的閾值為 5,SAOS-SART-B的顯著性水平為 0.4,即置信水平為 0.6.所有算法中的松弛參數(shù)均為 0.5.

圖1顯示了以上 3種算法從無噪聲投影數(shù)據(jù)迭代 10次的歸一化距離判據(jù).從圖1中可以看到,SAOS-SART的收斂速度明顯較 OS-SART快,而 SAOS-SART-A和 SAOS-SART-B有著幾乎相同的收斂速度.

圖2給出了以上 3種方法從無噪聲投影數(shù)據(jù)迭代 3次的重建切片.

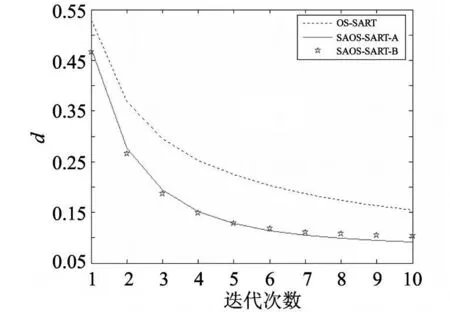
圖1 無噪聲投影數(shù)據(jù)重建切片的歸一化距離判據(jù)Fig.1 Normalized root criteria for slice reconstruction from noiseless projection data

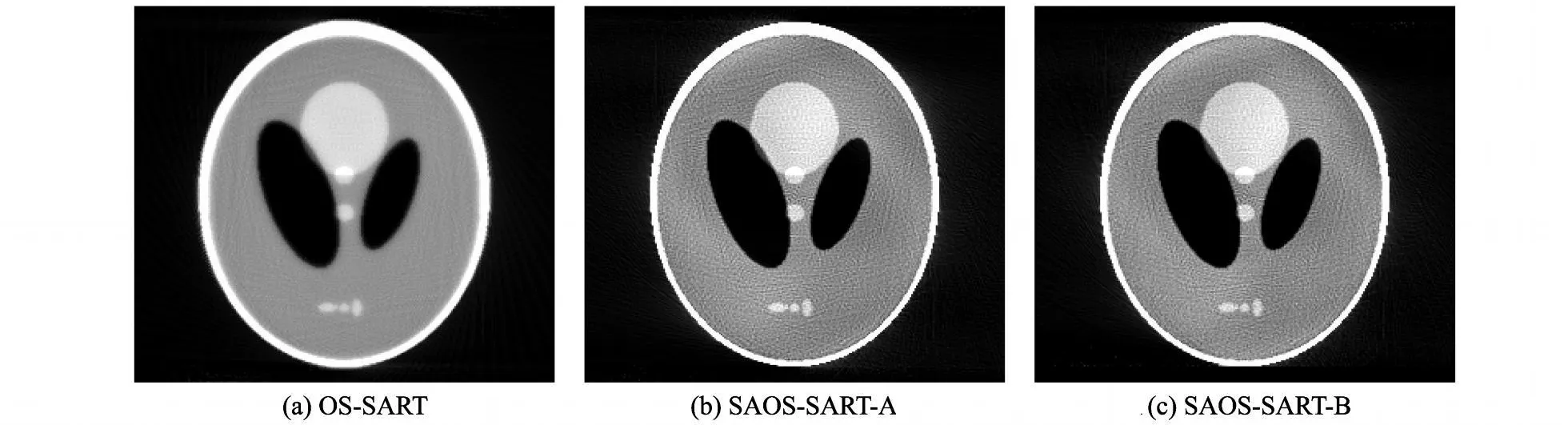
圖2 無噪聲投影數(shù)據(jù)迭代 3次后的 Shepp-Logan切片F(xiàn)ig.2 Reconstruction of the Shepp-Logan slice from noiseless projection data after 3 iterations

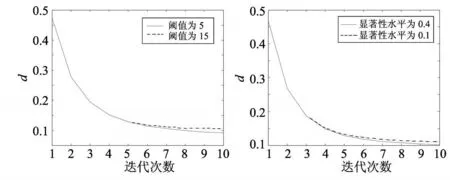
圖3 不同閾值和顯著性水平下的歸一化距離判據(jù)Fig.3 Normalized root criteria with different thresholds and different significant lev els

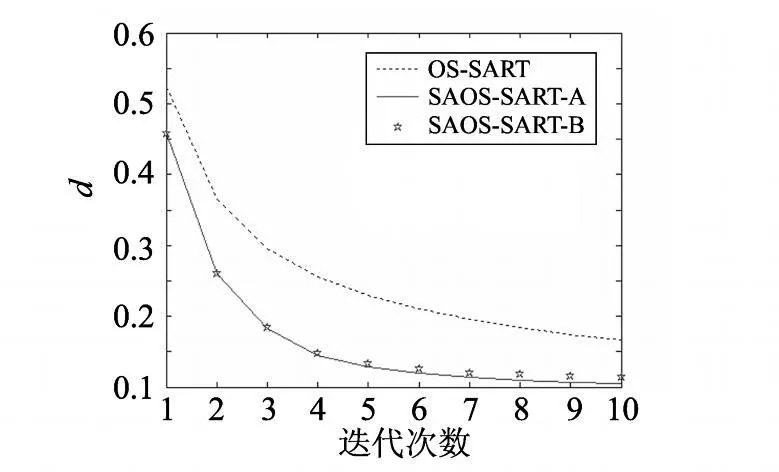
圖4 噪聲投影數(shù)據(jù)重建切片的歸一化距離判據(jù)Fig.4 Normalized root criteria for slice reconstruction from noisy projection data

在統(tǒng)計自適應(yīng)子集算法中,閾值和顯著性水平對重建速度是有影響的.一般來說,閾值越小或者顯著性水平越大(置信水平越小),收斂速度越快;反之,則收斂速度慢.圖3給出了不同閾值和顯著性水平下的歸一化距離判據(jù).由圖3可以看出,在前幾次迭代時,不同的閾值和顯著性水平對算法的影響非常小,這是因為顯著性水平大(置信水平小),子集內(nèi)的統(tǒng)計信息量小,即子集內(nèi)所包含的投影數(shù)較少(子集數(shù)目較大),圖像更新次數(shù)多;而當顯著性水平小(置信水平大)時,子集內(nèi)的統(tǒng)計信息大,彌補了圖像更新次數(shù)少這一缺點.但隨著迭代次數(shù)的增加,顯著性水平大,更新次數(shù)多的優(yōu)勢就越來越明顯了.

圖4顯示了以上 3種算法從噪聲投影數(shù)據(jù)迭代 10次的歸一化距離判據(jù),圖5給出了以上 3種方法從噪聲投影數(shù)據(jù)迭代 3次的重建切片.

圖5 噪聲投影數(shù)據(jù)迭代 3次后的 Shepp-Logan切片F(xiàn)ig.5 Reconstruction of the Shepp-Logan slice from noisy projection data after 3 iterations

4 結(jié) 論

本文提出了一種基于假設(shè)檢驗的統(tǒng)計自適應(yīng)子集算法,該方法每次迭代時可以對每個像素動態(tài)地生成子集,雖然每個子集的大小(即子集內(nèi)含投影的數(shù)目)不一樣,但子集內(nèi)的統(tǒng)計信息是相同的.本文還提出了兩個生成子集的統(tǒng)計量,第一個統(tǒng)計量形式簡單,適用于各種圖像;第二個統(tǒng)計量統(tǒng)計意義明確,卻只適用于可行性圖像,重建速度可通過調(diào)節(jié)閾值和顯著性水平來控制.由實驗結(jié)果可以看出,閾值為5的 SAOS-SART-A和顯著性水平為 0.4的 SAOS-SART-B收斂速度是幾乎相當?shù)?

在實驗的過程中,還發(fā)現(xiàn)了一個有趣的現(xiàn)象,算法在前期迭代中對含有噪聲的投影數(shù)據(jù)反而會得到較小的歸一化距離判據(jù),作者認為這可以從統(tǒng)計的角度去理解.在統(tǒng)計中,方差即信息量,方差大即信息量大,而含有噪聲的投影數(shù)據(jù)的方差是較大的,當然隨著迭代次數(shù)的增加,這種信息量的影響會逐漸變成負面的.

[1]Gordon R,Bender R,Herman G T.Algebraic reconstruction techniques(ART)for three-dimensional electron microscopy and X-ray photography[J].Journal of Theoretical Biology,1970,29(3):471-481.

[2]Andersen A H,Kak A C.Simultaneous algebraic reconstruction technique(SART):A superior implementation of the ART algorithm[J].Utrason.Ima.,1984,6:81-94.

[3]Cimmino G.Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari[J].Ricerca Sci.Ⅱ,1938,9:326-333.

[4]Censor Y,Elfving T.Blockalgorithms with diagonally scaled oblique projections for the linear feasibility problem[J].SIAM J.Matrix Anal.Applicat.,2002,24:40-58.

[5]Censor Y,Gordon D,Gordon R.Component averaging:an efficient iterative parallel algorithm for largeand sparse unstructured problems[J].Parallel Computing,2001,27:777-808.

[6]Hudson H M,Larkin R S.Accelerated image reconstruction using ordered subset of projection data[J].IEEE Transactions on Medical Imaging,1994,13(4):601-609.

[7]Kadrmas D J.Statistically regulated and adaptive EM reconstruction for emission computed tomography[J].IEEE Trans.on Nucl.Sci.,2001,48(3):790-798.

[8]Jiang M,Wang G.Convergence studies on iterative algorithms for image reconstruction[J].IEEE Trans.on Medical Imaging,2003,22:569-579.

[9]盛驟,謝世千.概率論與數(shù)理統(tǒng)計[M].第 3版.北京:高等教育出版社,2003:213-231.

[10]Llacer J,Veklerov E.Feasible image and practical stopping rules for iterative algorithms in emission tomography[J].IEEE Trans.Med.Imag.,1989,8(2):186-192.

[11]Wang G,Jiang M.Ordered-subset simultaneous algebraic reconstruction techniques(OS-SART)[J].Journal of XRay Science and Technology,2004,12:169-177.