景占策, 侯耀平

(1.青海師范大學(xué)數(shù)學(xué)系,青海西寧 810008; 2.湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)院,湖南長(zhǎng)沙 410081)

圖類αKa∪βCP(b)中的整譜圖

景占策1, 侯耀平2

(1.青海師范大學(xué)數(shù)學(xué)系,青海西寧 810008; 2.湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)院,湖南長(zhǎng)沙 410081)

設(shè)圖G是一個(gè)簡(jiǎn)單圖,圖G的補(bǔ)圖記為ˉG,如果G的譜都是整數(shù),就稱G是整譜圖.雞尾酒會(huì)圖CP(n)=K2n-n K2(K2n是2n階完全圖)和完全圖Ka都是整譜圖[1].本文確定了圖類中的所有整譜圖.

整譜圖;主特征值;丟番圖方程;雞尾酒會(huì)圖;完全圖

1 引 言

設(shè)G是一個(gè)簡(jiǎn)單連通圖,G的鄰接矩陣A(G)的特征值和特征向量稱為圖G的特征值和特征向量. G的一個(gè)特征值μ稱為主特征值,如果G有一個(gè)相應(yīng)于μ的各分量之和不為零的特征向量.由非負(fù)矩陣的理論知,圖的最大特征值(譜根)總是它的主特征值.一個(gè)圖恰有一個(gè)主特征值當(dāng)且僅當(dāng)它是正則圖.對(duì)恰有k(k≥2)個(gè)主特征值的圖的刻劃是圖譜理論中的一個(gè)長(zhǎng)期待解決的公開問(wèn)題.如果G的譜完全由整數(shù)組成,我們就說(shuō)G是整譜圖.Mirko Lepovic對(duì)恰有兩個(gè)主特征值的整譜圖的補(bǔ)圖做了較多研究,得到了一些很好的結(jié)果[4-8].

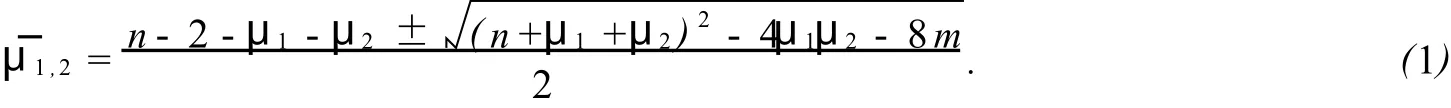
2 主要結(jié)論的證明及應(yīng)用

現(xiàn)在我們刻畫類整譜圖(α,β,a,b∈N,a-2b+1≠0).

[1] 柳柏濂.組合矩陣論[M].北京：科學(xué)出版社,2005：10-50.

[2] 侯耀平.恰有兩個(gè)主特征值的樹[J].湖南師范大學(xué)自然科學(xué)學(xué)報(bào),2005,28(2)：1-3.

[3] Lepovic M.Some results on graphs w ith exactly two main eigenvalues[J].Univ.Beogra Publ.Elektro-tehn. (Ser.Mat),2001,12(2)：68-84.

[4] Lepovic M.On integral graphs w hich belong to the class[J].J.App l.Math.&Computing,2004, 14(1-2)：39-49.

[5] Lepovic M.On integral graphs w hich belong to the class[J].Graphs and Combinatorics,2003,19：527-532.

[6] Lepovic M.On integral graphs w hich belong to the class[J].Discrete Mathematics,2004,285：183-190.

[7] Lepovic M.On integral graphs w hich belong to the class[J].Univ.Beograd.Publ.Fak.Ser. Mat.,2006,17：52-59.

[8] Lepovic M.On integral graphs w hich belong to the class[J].J.App l.Math.&Computing,2006, 20(1-2)：61-74.

On In tegral Graphs Which Belong to the ClassαKa∪βCP(b)

J ING Zhan-ce1,HOU Yao-ping2
(1.Department of Mathematics,Qinghai No rmal University,Xining,Qinghai 810008,China; 2.College of Mathematics and Computer Sciences,Hunan No rmal University,Changsha,Hunan 410081,China)

LetGbe a simp le graph and letˉGdenote its complement.A graphGis called integral if its spectrum consists entirely of integers.Cocktail party graphsCP(n)=K2n-n K2and complete graphsKaall are integral graphs[1]. This paper determines all the integral graphs of

integral graphs;main eigenvalues;Diophantion equation;Cocktail party graphs;comp lete graphs

O157.5

A

1672-1454(2010)02-0113-05

2007-07-14

湖南省教育廳科學(xué)研究資助項(xiàng)目(06A 037)