sin+sin+sin≥3·的一個隔離及類似

●

(天津港口管理中專 天津 300456)

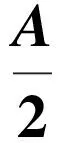
●黃兆麟

(天津港口管理中專 天津 300456)

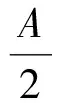
以上是《數(shù)學通報》2009年第2期刊出的1 779號問題,本文給出其一個隔離及其類似命題,供參考.

命題1△ABC的外接圓與內切圓半徑分別為R,r,證明：

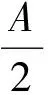
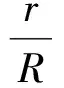
(1)

引理1若△ABC的外接圓與內切圓半徑分別為R,r,則

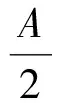
證明設△ABC的3條邊長分別為a,b,c,則由面積公式及正弦定理,可得

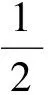
因此 2RsinB·2RsinC·sinA=

(2RsinA+2RsinB+2RsinC)r.

于是

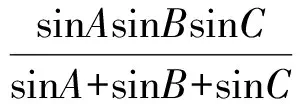
從而

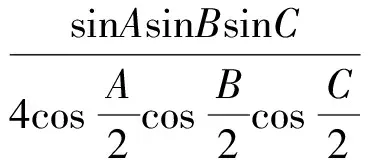
故

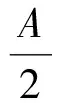
引理2(Euler不等式)若△ABC的外接圓與內切圓半徑分別為R,r,則R≥2r.

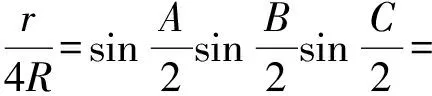
R≥2r.

下面證明命題1.

證明先證式(1)中的第1個不等式.

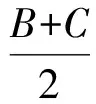
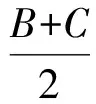
所以

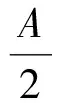
同理可得

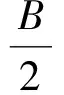
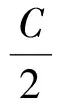
以上3個式子相加化簡即得

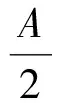
再利用2個引理證式(1)中的第2個不等式.

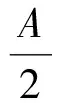
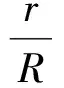
可得

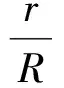
至此,式(1)得證.

命題2△ABC的外接圓與內切圓半徑分別為R,r,證明：

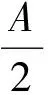
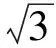
(2)

證明先證式(2)中的第1個不等式.

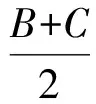
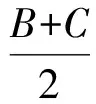
所以

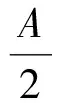
同理可得

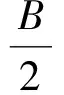
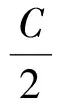
以上3個式子相加化簡即得

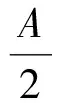
再證式(2)中的第2個不等式.

可得

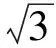
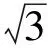
于是

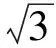
至此,式(2)得證.