陳紅兵,何萬生

(天水師范學院數(shù)學與統(tǒng)計學院,甘肅 天水 741001)

一類具有收獲率競爭系統(tǒng)的穩(wěn)定性及Hopf分岔

陳紅兵,何萬生

(天水師范學院數(shù)學與統(tǒng)計學院,甘肅 天水 741001)

首先建立了一類具有時滯的捕獲率的競爭系統(tǒng),該系統(tǒng)具有Holling II功能.接著應用特征方程,發(fā)現(xiàn)當τ穿過某些數(shù)時出現(xiàn)了Hopf分岔,并用規(guī)范型方法和中心流形定理得到Hopf分岔和分岔周期解的穩(wěn)定性的計算公式.最后舉例論證.

競爭;穩(wěn)定性;平衡點;Hopf分岔

1 引言

受到文獻[1-5]的啟發(fā),本文建立具有收獲率的時滯Holling II功能反應系統(tǒng):

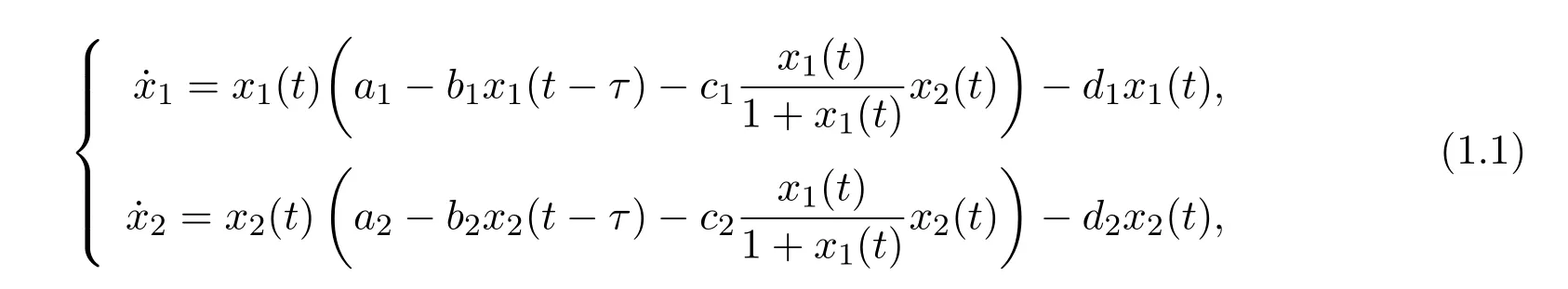
2 有界性

3 Hopf分岔的存在性

4 Hopf分岔與分岔周期解的計算公式

5 舉例

[1]陳蘭蓀.數(shù)學生態(tài)學建模與研究方法[M].北京:科學教育出版社,1988.

[2]馬知恩.種群生態(tài)學的數(shù)學建模與研究[M].安徽:安徽教育出版社,1996.

[3]Faria T.Stability and bifurcation for a delayed predator-prey model and the e ff ect of di ff usion[J].J.Math. Appl.,2001,254:433-463.

[4]Yan X P,Li W T.Hopf bifurcation and global periodic solutions in a delayed predator–prey system[J]. Appl.Math.Comput.,2006,177:427-445.

[5]May R M.Time delay versus stability in population models with two and three trophic levels[J].Ecology, 1973,4:315-325.

[6]Hassard B,Kazarino ffD,Wan Y.Theory and Applications of Hopf Bifurcation[M].Cambridge:Cambridge University Press,1981.

[7]Meng X,Wei J.Stability and bifurcation of mutual system with time delay[J].Chaos,Solitons and Fractals, 2004,21:729-40.

[8]Hale J,Lunel S M.Introduction to Functional Di ff erential Equations[M].New York:Springer,1993.

[9]Ruan S,Wei J.On the zeros of transcendental functions with applications to stability of delay di ff erential equations with two delays[J].Dyn.Contin.Discrete Impuls.Syst.Ser.A Math.Anal.,2003,10:863-874.

[10]許丹丹,李艷玲,吳迪.一類帶擴散項的 HIV系統(tǒng)的平衡解的穩(wěn)定性分析 [J].純粹數(shù)學與應用數(shù)學, 2011,27(3):369-375.

The Hopf bifurcation and stability of competitive system with rate harvesting

Chen Hongbing,He Wansheng
(School of Mathematics and Statistics Tianshui Normal University,Tianshui741001,China)

First,established a competitive mold with Holling II functional response.Further,by analyzing the associated characteristic equation,it is founded that Hopf bifurcation occurs when τ crosses some critical value. The direction of Hopf bifurcation as well as stability of periodic solution are studied.The method which we used is the normal form theory and center manifold method.An example showed the feasibility of results.

compete,stability,equilibrium point,Hopf bifurcation

圖1 τ=1平衡點漸近穩(wěn)定

圖2 τ=3 Hopf分岔及周期解穩(wěn)定

O175.14

A

1008-5513(2012)05-0604-10

2012-04-10.

甘肅省自然科學基金(096RJZE106).

陳紅兵(1983-),碩士,講師,研究方向：應用微分方程.

2010 MSC:34D12