基于粒子群算法的捕食者-食餌模型的參數(shù)估計(jì)

劉利斌,劉翠萍,張永,王勇

(1.池州學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院,安徽池州　247000; 2.西北核技術(shù)研究所,陜西西安　710024)

?

基于粒子群算法的捕食者-食餌模型的參數(shù)估計(jì)

劉利斌1,劉翠萍1,張永1,王勇2

(1.池州學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院,安徽池州247000; 2.西北核技術(shù)研究所,陜西西安710024)

摘要：針對(duì)捕食者-食餌模型參數(shù)估計(jì)問題,基于三次Hermite插值多項(xiàng)式,提出了一種基于粒子群優(yōu)化算法的高精度參數(shù)估計(jì)方法.數(shù)值仿真實(shí)驗(yàn)表明,本文提出的參數(shù)估計(jì)方法可以更精確地計(jì)算出相關(guān)參數(shù).

關(guān)鍵詞：捕食者-食餌模型;粒子群算法;參數(shù)估計(jì)

1　引言

在自然界中,不同種群之間存在一種相互依存又相互制約的生存方式.例如種群甲靠豐富的自然資源生存,而種群乙靠捕食甲為生,這就形成了捕食者-食餌系統(tǒng).常用的捕食者-食餌模型具有如下形式:

其中, x(t)和y(t)分別表示食餌種群和捕食者種群在t時(shí)刻的數(shù)目; f[x(t)]和g[y(t)]分別表示食餌種群和捕食者種群在t時(shí)刻的增長(zhǎng)率; p[x(t)]為捕食者種群對(duì)食餌種群的功能性反應(yīng)函數(shù), k為已知的常數(shù).

對(duì)于捕食者-食餌模型的理論分析,一些學(xué)者已經(jīng)進(jìn)行了系統(tǒng)的研究[1-3].近年來(lái),捕食者-食餌模型的參數(shù)估計(jì)問題越來(lái)越受到許多學(xué)者的關(guān)注.文獻(xiàn)[4]研究了一類微分方程的參數(shù)反演問題,并提出了一種樣條最小二乘算法.文獻(xiàn)[5]考慮經(jīng)典的捕食者-食餌模型的參數(shù)估計(jì)問題,給出了求解這類參數(shù)估計(jì)問題的信賴域方法.文獻(xiàn)[6-7]討論了捕食者-食餌模型的兩階段參數(shù)估計(jì)法,并得到了參數(shù)的估計(jì)值和置信區(qū)間.文獻(xiàn)[8]首先利用三點(diǎn)的四階差分格式對(duì)捕食者-食餌模型中的一階導(dǎo)數(shù)進(jìn)行了離散,并將其參數(shù)估計(jì)問題轉(zhuǎn)化成一個(gè)無(wú)約束的優(yōu)化問題,然后提出了一種混合加速粒子群算法來(lái)求解該優(yōu)化問題.為了進(jìn)一步提高捕食者-食餌模型參數(shù)估計(jì)的精度,本文基于三次Hermite插值函數(shù),得出一個(gè)具有五階精度的數(shù)值積分公式,并將該積分公式應(yīng)用于捕食者-食餌模型數(shù)值離散,同時(shí)可得到相應(yīng)的無(wú)約束優(yōu)化問題.接著,利用基本的粒子群算法對(duì)該優(yōu)化問題進(jìn)行求解.與目前已有的算法相比,本文提出的參數(shù)估計(jì)方法的精度明顯更高一些.

2　三次Hermite插值多項(xiàng)式與數(shù)值積分公式的構(gòu)造

對(duì)于給定函數(shù)F : [x0,x1]→C[x0,x1],滿足插值條件

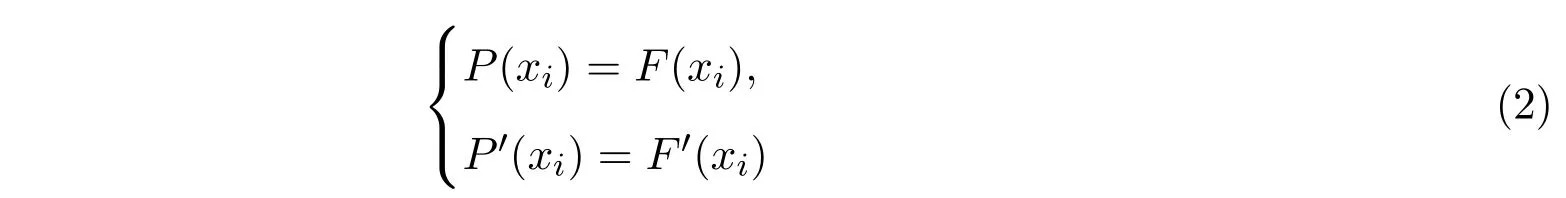
的三次Hermite插值多項(xiàng)式[9]可表示為:

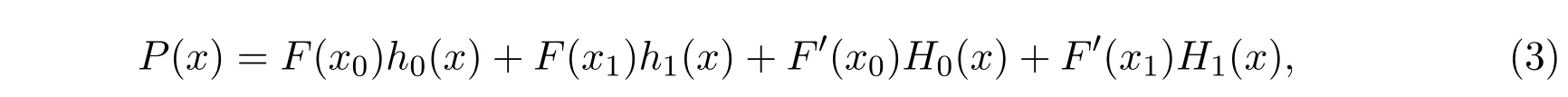
其中

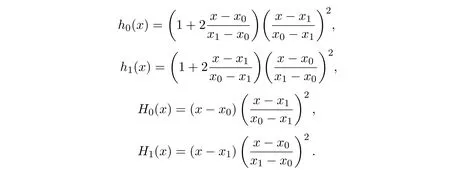
對(duì)于三次Hermite插值多項(xiàng)式(3),有如下的誤差估計(jì):

定理1.1[9]對(duì)于任意的實(shí)數(shù)x0, x1(x0＜x1),函數(shù)f(x)∈C4[x0,x1],若p(x)是三次的Hermite插值多項(xiàng)式,則對(duì)任意的x∈[x0,x1],都存在一個(gè)ξ∈[x0,x1],使得

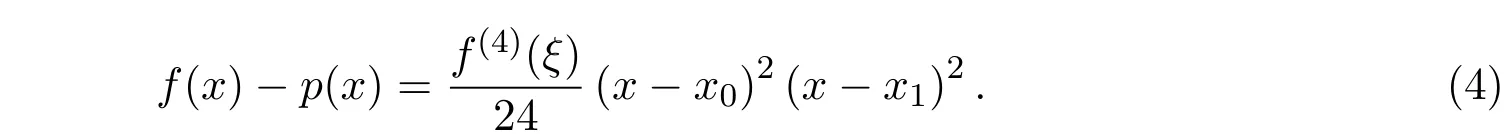
進(jìn)一步,由定理1可得如下數(shù)值積分公式:

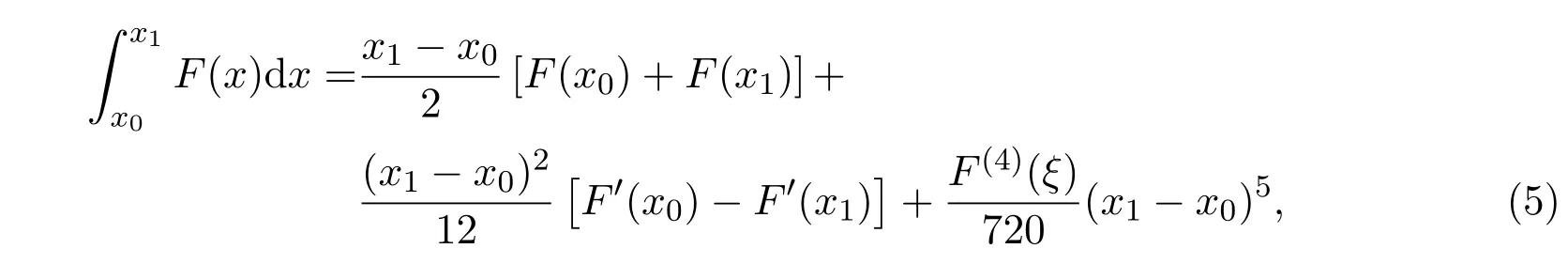
其中ε∈[x0,x1].

3　捕食者-食餌模型的參數(shù)估計(jì)

考慮如下捕食者-食餌模型:

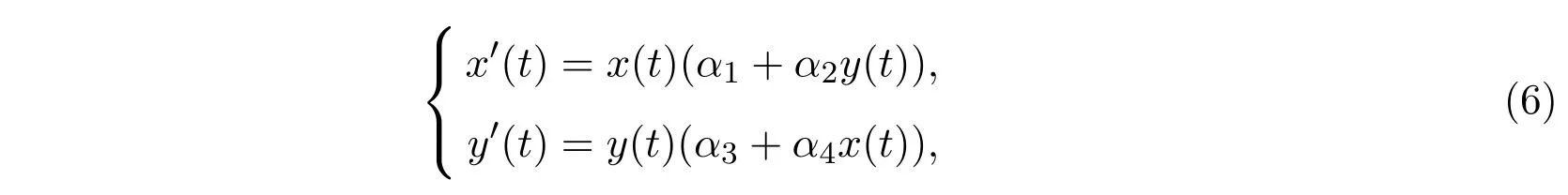
初始條件為x(t0) =α5, y(t0) =α6,其中αi(i = 1,···,6)是待求的參數(shù).

顯然,方程(6)為非線性常微分方程組,很難求出其解析解.因此,對(duì)于給定四個(gè)參數(shù)(α1,α2,α3,α4)和初始條件α5,α6,可采用數(shù)值方法進(jìn)行求解.為了方便,稱(α1,α2,α3,α4)為狀態(tài)參數(shù),初始值α5,α6為初值參數(shù).

一般情況下,對(duì)于x(t), y(t)的一組測(cè)量數(shù)據(jù)

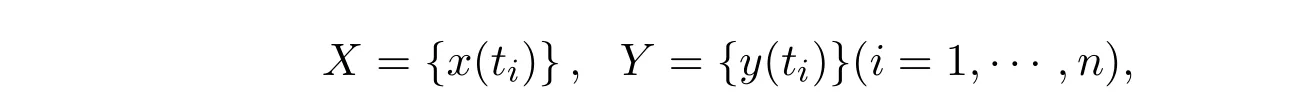
可將模型(6)中的參數(shù)估計(jì)問題轉(zhuǎn)化為如下無(wú)約束的非線性優(yōu)化問題:

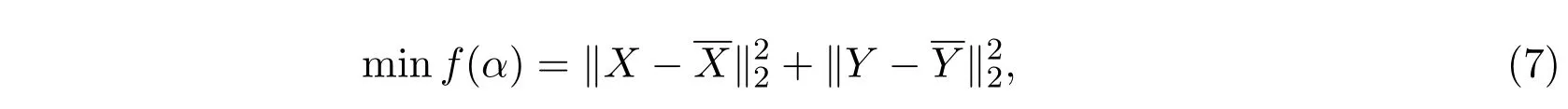
其中α= (α1,α2,α3,α4)為未知參數(shù), X, Y為測(cè)量數(shù)據(jù),為估計(jì)值.

接下來(lái),為了得出目標(biāo)函數(shù)(7)的具體表達(dá)式,利用(5)式對(duì)模型(6)進(jìn)行離散,得

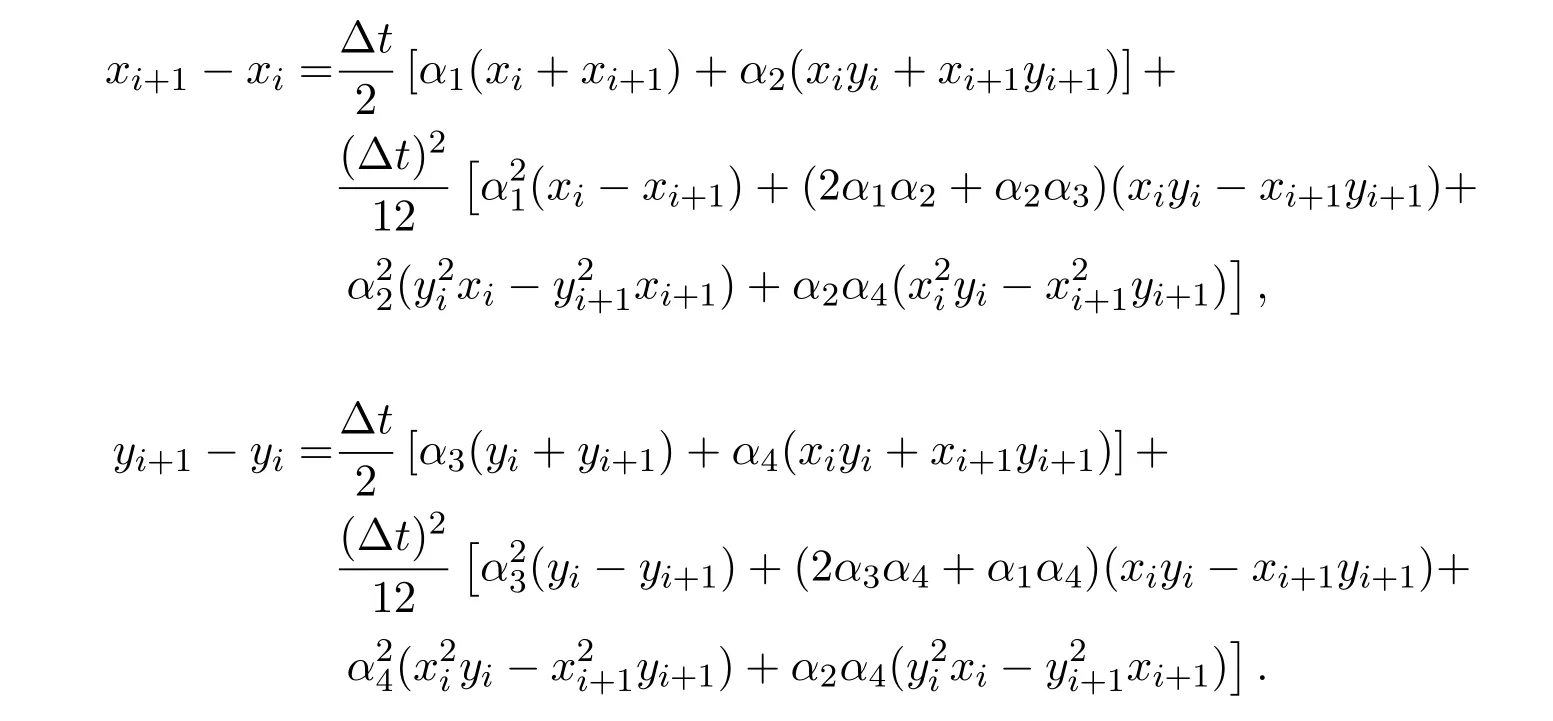
于是,目標(biāo)函數(shù)(7)可轉(zhuǎn)化為如下非線性優(yōu)化問題

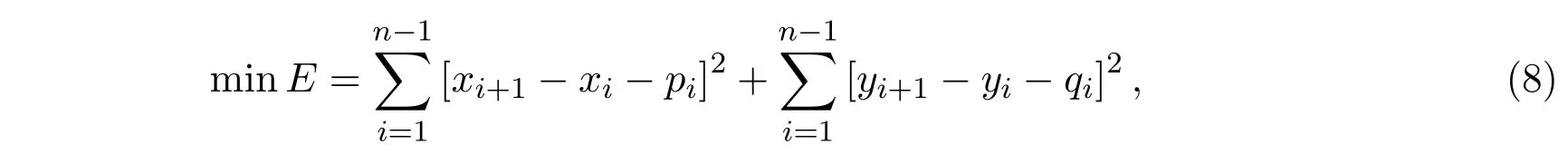
其中

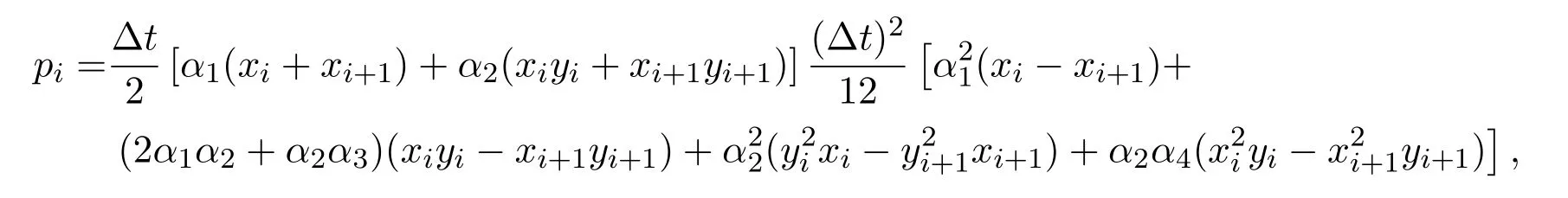
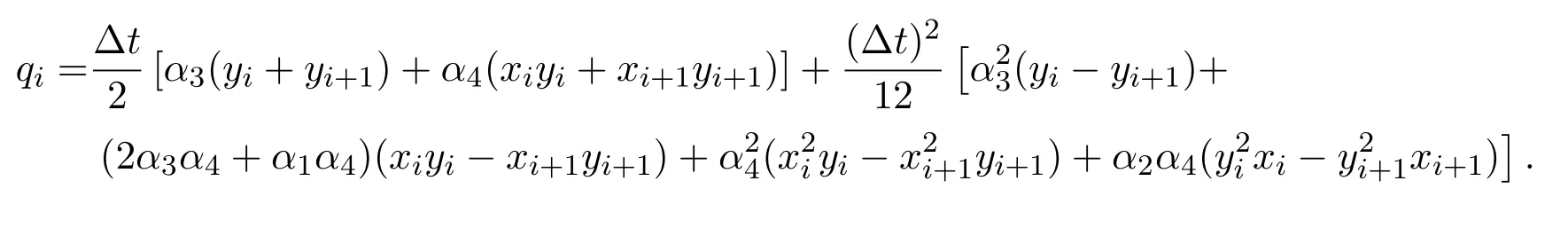
4　基本粒子群算法簡(jiǎn)介

粒子群算法(Particle Swarm Optimization),又稱PSO算法,是由Eberhart博士和Kennedy博士在1995年提出的一種基于群體智能演化的計(jì)算技術(shù)[10].該算法最早是受到鳥群活動(dòng)的規(guī)律性啟發(fā),進(jìn)而利用群體智能建立起來(lái)的一個(gè)簡(jiǎn)化模型. PSO算法在對(duì)種群活動(dòng)行為觀察基礎(chǔ)上,利用群體中的個(gè)體對(duì)信息的共享使整個(gè)群體的運(yùn)動(dòng)在問題空間中產(chǎn)生無(wú)序到有序的進(jìn)化過程,從而獲得最優(yōu)解.與遺傳算法相比,它沒有遺傳算法的“交叉”和“變異”操作,它通過追逐當(dāng)前搜索的最優(yōu)值來(lái)尋找全局最優(yōu). PSO算法以其實(shí)現(xiàn)容易、精度高、收斂快等優(yōu)點(diǎn)引起了許多學(xué)者的關(guān)注,并且在參數(shù)估計(jì)中展示了其優(yōu)越性,見文獻(xiàn)[11-15].粒子群算法迭代過程如圖1所示.

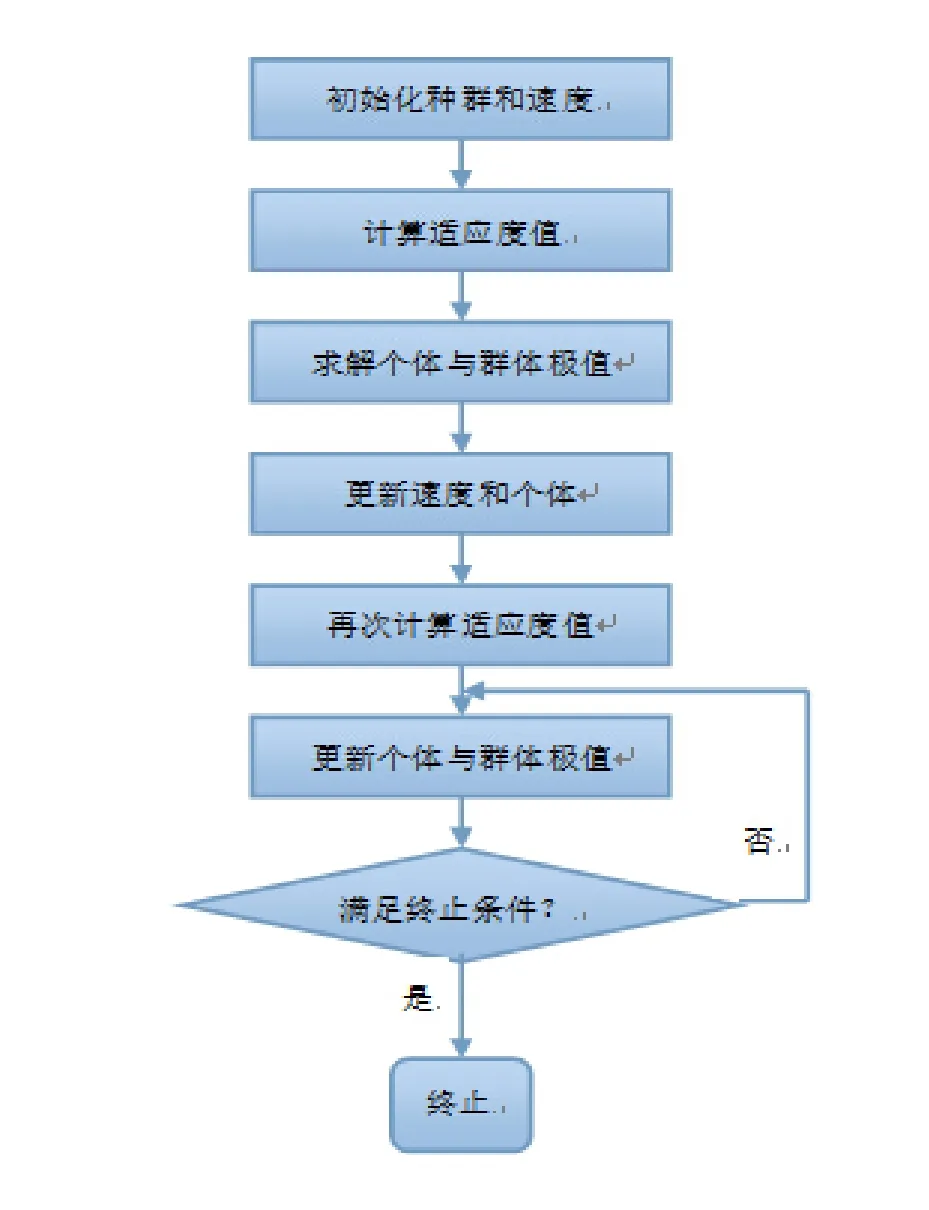
圖1　PSO算法的流程圖

5　數(shù)值實(shí)驗(yàn)與結(jié)果分析

在這里,以2006年全國(guó)研究生數(shù)學(xué)建模競(jìng)賽B題數(shù)據(jù)為例,驗(yàn)證本文方法的有效性,其中狀態(tài)參數(shù)的真值為α= (2,?0.1,?10,1,13,72),時(shí)間區(qū)間[0,15],采樣時(shí)間步長(zhǎng)?t = 0.1.另外,為了方便計(jì)算,將測(cè)量數(shù)據(jù)的第一組數(shù)據(jù)定為初值參數(shù)的估計(jì)值,即α5= 12.9622, α6= 72.1230.于是,在后面的計(jì)算結(jié)果中,只需計(jì)算α1,α2,α3,α4即可. PSO算法的參數(shù)設(shè)置為:最大迭代次數(shù)為50次,粒子數(shù)N = 200,加速常數(shù)c1= 1.2, c2= 1.2,狀態(tài)參數(shù)范圍αi∈[?11,11](i = 1,···,4).

接下來(lái),采用粒子群算法對(duì)目標(biāo)函數(shù)(8)進(jìn)行求解,狀態(tài)參數(shù)的計(jì)算結(jié)果見表1.同時(shí),為了驗(yàn)證本文方法的優(yōu)越性,表1中也列出了文獻(xiàn)[7-8]的計(jì)算結(jié)果.在這里,表1中狀態(tài)參數(shù)的誤差采用如下式子進(jìn)行計(jì)算,

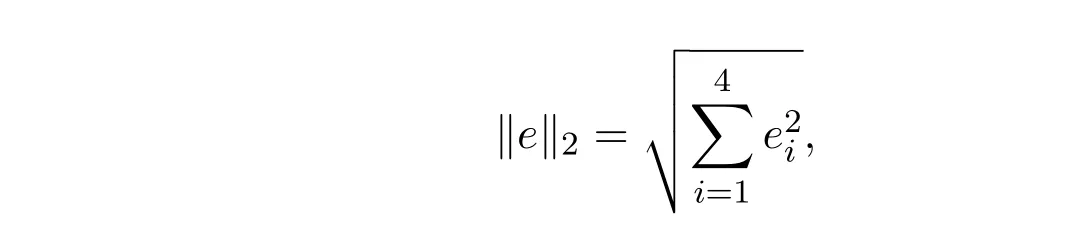
其中ei(i = 1,2,3,4)為各參數(shù)的估計(jì)值與真實(shí)值之間的差.

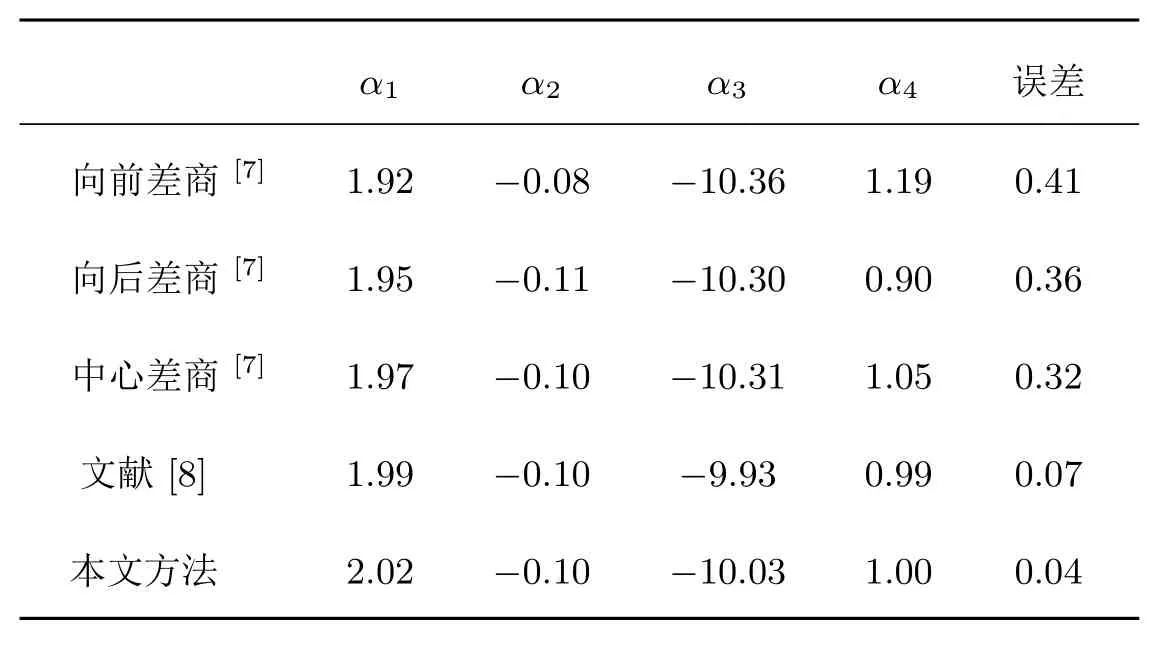
表1　不同算法計(jì)算得到的狀態(tài)參數(shù)及誤差

最后,將本文計(jì)算的結(jié)果代入模型(6),用Runge-Kutta法求得其數(shù)值并進(jìn)行仿真,得出x(t)和y(t)的擬合曲線,如圖2,圖3所示.從圖中可以看出,計(jì)算得到的結(jié)果和實(shí)際測(cè)量得到的結(jié)果是相當(dāng)吻合的.

6　結(jié)論

對(duì)于捕食者-食餌模型的參數(shù)估計(jì)問題,本文首先結(jié)合三次Hermite插值多項(xiàng)式,提出了一個(gè)高精度的數(shù)值積分公式,并將其應(yīng)用于捕食者-食餌模型的離散.值得一提的是該數(shù)值積分公式只需兩個(gè)節(jié)點(diǎn)的函數(shù)值和導(dǎo)數(shù)值.然后,為了克服經(jīng)典迭代優(yōu)化算法對(duì)參數(shù)初值的依賴,采用了粒子群優(yōu)化算法對(duì)捕食者-食餌模型的參數(shù)進(jìn)行求解.數(shù)值實(shí)驗(yàn)表明本文提出的參數(shù)估計(jì)方法具有較高的精度.

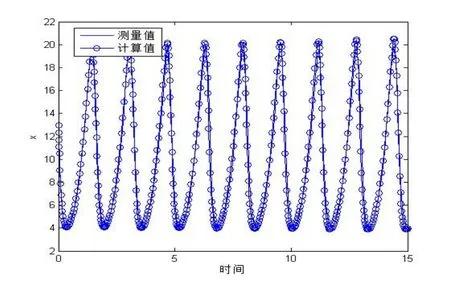
圖2　x(t)的測(cè)量與計(jì)算值的仿真結(jié)果比較

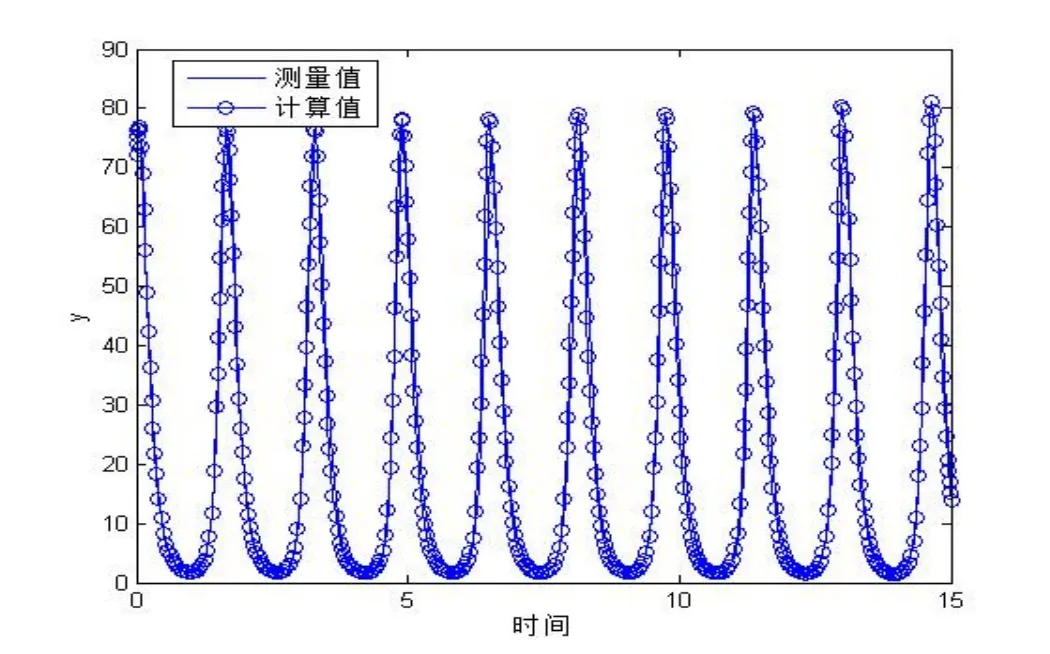
圖3　y(t)的測(cè)量與計(jì)算值的仿真結(jié)果比較

參考文獻(xiàn)

[1]王玲書.一個(gè)具有時(shí)滯和階段結(jié)構(gòu)的捕食-被捕食者模型的穩(wěn)定性[J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào), 2013,28(4):466-476.

[2]肖氏武,王穩(wěn)地,金瑜.一類具有階段結(jié)構(gòu)的捕食者-食餌模型的漸進(jìn)性質(zhì)[J].生物數(shù)學(xué)學(xué)報(bào), 2007,22(1):37-45.

[3]張亮亮,張麗娜.一類三種群捕食者-食餌模型中交錯(cuò)擴(kuò)散導(dǎo)致的Turing不穩(wěn)定[J].應(yīng)用數(shù)學(xué), 2014,27(1):82-87.

[4] Varah J. M. A spline least squares method for numerical parameter estimation in differential equations [J]. SIAM Journal on scientific computing, 1982,3:28-46.

[5] Jerome M B, Walmag, Eric J M, et al. A trust-region method applied to parameter identification of a simple prey-predator model [J]. Applied Mathematical Modeling, 2005,29(3):289-307.

[6]馬新生,王來(lái)群,胡文玉.基于潛周期模型的兩種群食餌-捕食者模型的參數(shù)估計(jì)[J].南昌大學(xué)學(xué)報(bào)(工科版) , 2008,30(2):134-137.

[7]馬新生,翁瑾.兩種群食餌-捕食者模型參數(shù)估計(jì)的數(shù)值微分法[J].南昌大學(xué)學(xué)報(bào)(工科版), 2010,32(1):741-796.

[8]曹懷火,李海燕,伏升茂.基于混合加速粒子群算法的捕食者-食餌模型參數(shù)估計(jì)[J].生物數(shù)學(xué)學(xué)報(bào), 2013,28(3):553-557.

[9] Kress R. Numerical Analysis [M]. Graduate Texts in Mathematics, 181. New York. Springer-Verlag, 1998.

[10] Kennedy J, Eberhart R C. Particle swarm optimization [C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway. New Jersey：Institute of Electrical and Electronics Engineers, Inc., 1995:1942-1948.

[11]韓寧,尚朝軒.基于粒子群優(yōu)化算法的LFM信號(hào)參數(shù)估計(jì)[J].計(jì)算機(jī)工程, 2012,38(4):176-178.

[12]燕振剛,胡賀年,李廣.基于粒子群優(yōu)化算法的Richards模型參數(shù)估計(jì)和算法有效性[J].計(jì)算機(jī)應(yīng)用, 2014,34(10):2827-2830.

[13]李斌,李文鋒.基于仿真的優(yōu)化的粒子群算法參數(shù)選取研究[J].計(jì)算機(jī)工程與應(yīng)用, 2011,47(33):30-35.

[14]郭建濤,王宏遠(yuǎn),余本海.基于粒子群算法的調(diào)頻信號(hào)參數(shù)估計(jì)[J].計(jì)算機(jī)應(yīng)用研究, 2010,27(2):512-514.

[15]劉錦萍,郁金祥.基于粒子群算法的Logistic回歸模型參數(shù)估計(jì)[J].計(jì)算機(jī)工程與應(yīng)用, 2009,45(33):42-44.

2010 MSC: 65L12

Parameter estimation method for predator prey model based particle swarm optimization algorithm

Liu Libin1, Liu Cuiping1, Zhang Yong1, Wang Yong2
(1. College of Mathematics and Computer, Chizhou University, Chizhou 247000, China; 2. Northwest Institute of Nuclear Technology, Xi′an 710024, China)

Abstract:For the problem of predator prey model parameter estimation, a high accuracy parameter estimation method based on particle swarm optimization algorithm is proposed, which is based on the cubic Hermite interpolation polynomial. It is shown from the numerical results that the proposed method can be more accurate.

Key words:predator prey model, particle swarm algorithm, parameter estimation

作者簡(jiǎn)介：劉利斌(1982-),博士,講師,研究方向:微分方程數(shù)值解法及智能計(jì)算.

基金項(xiàng)目：國(guó)家自然科學(xué)基金(11301044);安徽省優(yōu)秀青年人才重點(diǎn)項(xiàng)目(2013SQRL095ZD);安徽省高校自然科學(xué)研究重點(diǎn)項(xiàng)目(KJ2015A213);安徽省大學(xué)生創(chuàng)新項(xiàng)目(AH201411306130).

收稿日期：2015-08-10.

DOI：10.3969/j.issn.1008-5513.2016.01.004

中圖分類號(hào)：O175.14

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1008-5513(2016)01-0019-07