Anti-plane Analysis of a Circular Hole with Three Unequal Cracks in One-dimensional Hexagonal Piezoelectric Quasicrystals?

YANG JuanLI Xing?DING Sheng-hu

(1-Institute of Ethnic Preparatory Education,Ningxia University,Yinchuan 750002;2-Institute of Mathematics and Computer Science,Ningxia University,Yinchuan 750021)

1 Introduction

As a class of smart materials,piezoelectric materials have been wide ly used in adaptive microelectro-mechanical systems such as sensors,actuators,and transducers due to a strong coupling characteristic between elastic and electric behavior[1;2].Now,piezoelectric sensors,actuators,and transducers of various configurations can be manufactured for specified functions[3].For example,in signal processing applications,with the aid of excitation or reception of the surface acoustic waves,an interdigital transducer is a thin piezoelectric layer bonded perfectly on a elastic substrate.And on the surface of the piezoelectric film,an array of electrodes is arranged according to different patterns[4].

Quasicrystal as a new structure and material was first observed by Shechtman et al[5]and announced in 1984.Experiments have shown that quasicrystals are quite brittle Meng et al[6]and the defects of quasicrystalline materials have been observed[7].It is well known that the presence of defects such as holes,cracks and dislocations,greatly affects the physical and mechanical properties of solid materials including quasicrystals.Therefore,the study of crack problem of quasicrystalline materials is meaningful both in theoretical and practical applications.Many studies on elastic problems and fracture mechanics in quasicrystals have been available.Fan[8]presented the mathematical theory of quasicrystalline elasticity.Using this theory,a straight dislocation and a moving screw dislocation in 1D hexagonal quasicrystals were addressed by Li and his coauthors[9;10].It is well known that the complex variable method initially developed by Muskhelishvili is an effective method for solving various elasticity and defect problems[11].Therefore,some workers developed the complex variable method to solve defect problems of quasicrystals.For 1D hexagonal quasicrystals many efforts have been maDein the fields of the mechanic involving the elasticity and defects[12-15].

But most of the paper mentioned before discussed various elasticity and defect problems of quasicrystals.To our knowledge,the piezoelectric quasicrystals researches are very little,especially the study of quasicrystals piezoelectric properties.Analytic solutions of two collinear fast propagating cracks in a symmetrical strip of 1D hexagonal piezoelectric quasicrystals have been studied[16].Yang and Li[17]investigated studied the anti-plane shear problem about a circular hole with a straight crack in 1D hexagonal quasicrystals with piezoelectric effects under the electrically impermeable and electrically permeable boundary condition.The present paper is devoted to investigating the elastic problem of a circular hole with three unequal cracks in 1D hexagonal piezoelectric quasicrystals by means of complex variable function method with conformal mapping.Two kinds of crack surface conditions,i.e.electrical impermeable and electrical permeable are adopted.The exact solutions of SIFs for the phonon field and the phason field,and the EDIFs are obtained respectively,which are very useful in practice.In the limiting cases,the analytic solutions of two asymmetric cracks,two symmetric cracks,and a straight crack originating from a circular hole the moDeLcrack and the Griffth crack[6]in 1D hexagonal piezoelectric quasicrystals are derived from the present solutions.Furthermore,in the absence of electric loading,the exact solutions of the field intensity factors presented in this paper can be degenerated into the corresponding results of in 1D hexagonal quasicrystals[18].The numerical results reveal the effects of geometric parameters on the field intensity factors.It is found that the horizontal crack length and the circle radius easily can promotes crack growth.

2 Basic theory

The generalized Hooke’s law of 1D hexagonal piezoelectric quasicrystals with point group 6mm,whose period plane is the(x1,x2)-plane and whose quasiperiodic direction is thex3-axis,is given by[8;13]

whereσij,3)are the phonon and phason stress components;are the electric fields and the electric displacements;εijare the phonon and phason strains;K1,K2 are elastic constants in the phason field;)are phonon-phason coupling elastic constants;e1ijare piezoelectric coefficients;∈11,∈33 are two dielectric coefficients are elastic constants in the phonon field.C11,C12,C13,C33,C44,C66 are elastic constants in the phonon field.

The strain-displacement and electric field-electric potential relations are given by

whereuiandvdenote the displacements of phonon field and phason field,?is the electric potential.Andthe same notation hereafter.

The equilibrium equations(if the body force and electric charge density are neglected)are given by

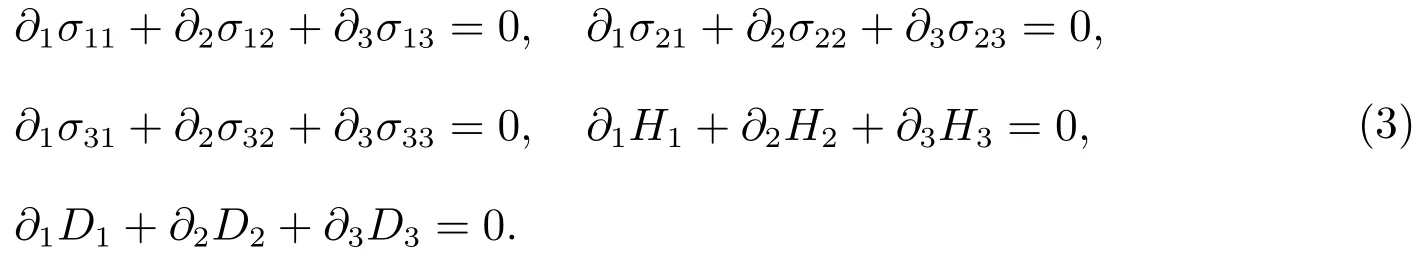
(1)–(3)are the basic equations of elasticity theory of 1D hexagonal piezoelectric quasicrystals.

It is assumed that the quasi-periodic direction of 1D hexagonal quasicrystals is along the positive direction ofx3axis.In this case,all field variables are independent ofx3and we have the following deformation geometrical equations

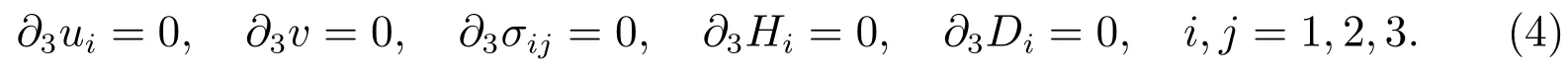
Substituting(4)into(1)–(3)leads to one is a plane elasticity problem of general crystals,which can be solved by the route of linear elastic theory[11].We do not discuss it here.And the other is an anti-plane coupling elasticity problem as follows

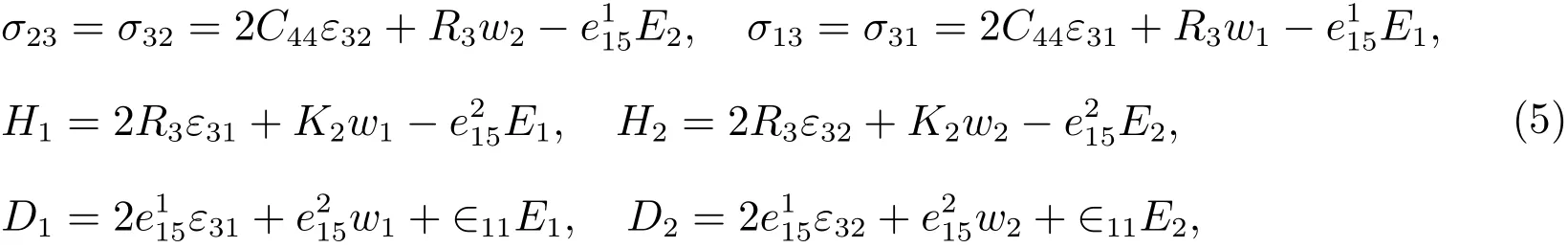
and

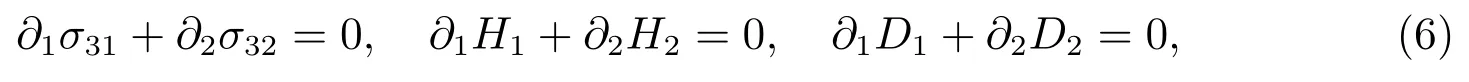
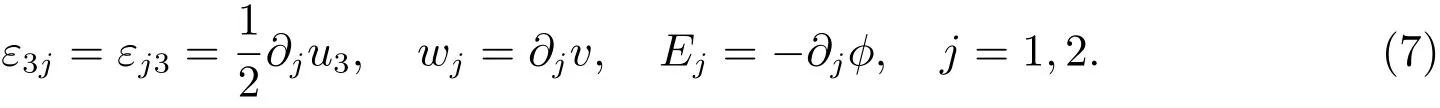
Insertion of(7)into(5)and with the aid of(6),one has

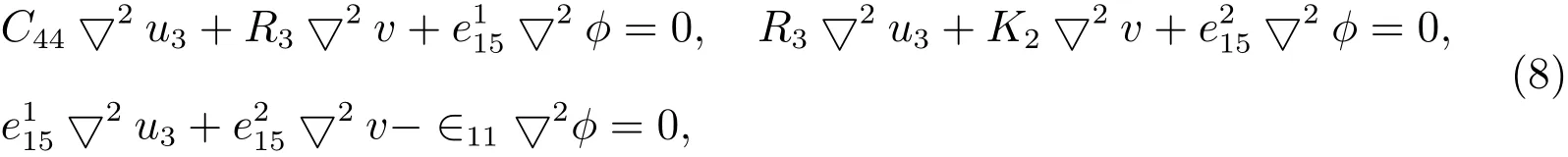
whereis the two dimensional Laplace operator,one obtain

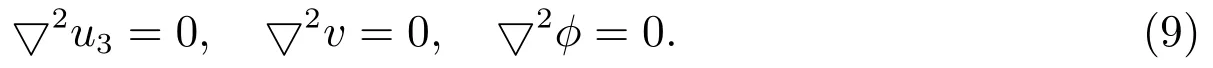
If

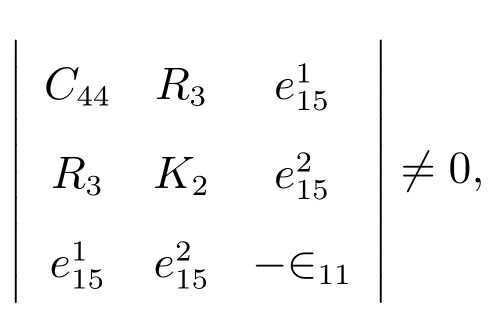
the general solution of(9)can be expressed as

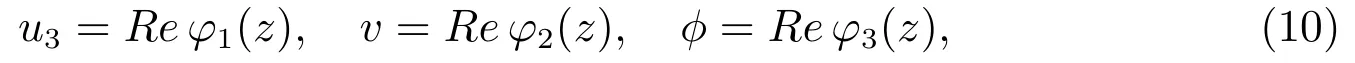
in whichare arbitrary three analytic functions.

3 Solution of elastic field

We consider three unequal cracks originating from a circular hole in a 1D hexagonal piezoelectric quasicrystals.It is assumed that the quasi-periodic direction of 1D hexagonal quasicrystals is along the positive direction ofx3axis.The solid is subjected to uniform remote anti-plane shear loading and in-plane electric loading as shown in Figure 1.Ris the circle radius,L1andL2are the horizontal crack lengths,andL3is the vertical crack length.

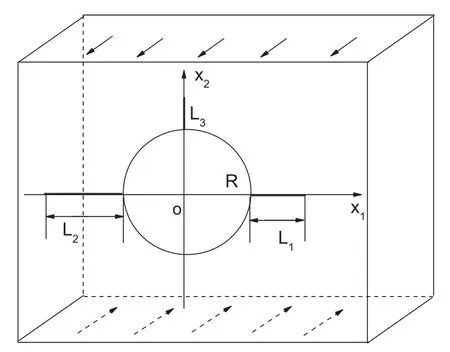
Figure1:A circular hole with three unequal cracks in 1D hexagonal piezoelectric quasicrystals

3.1 Electric impermeable problem

That by the linear elastic theory,this problem can be considered only in the crack surface stressthe electric impermeable boundary condition can be expressed as

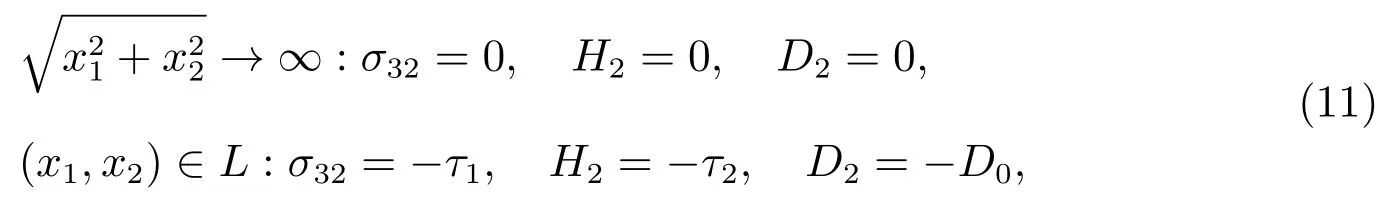
whereLdenotes the boundary of the circular hole with three unequal cracks.

By(5)and(10),the stresses and the electric displacements can be written as

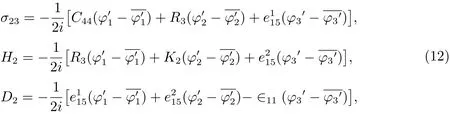
where

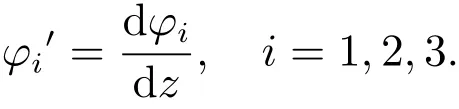
From(11)and(12),we have

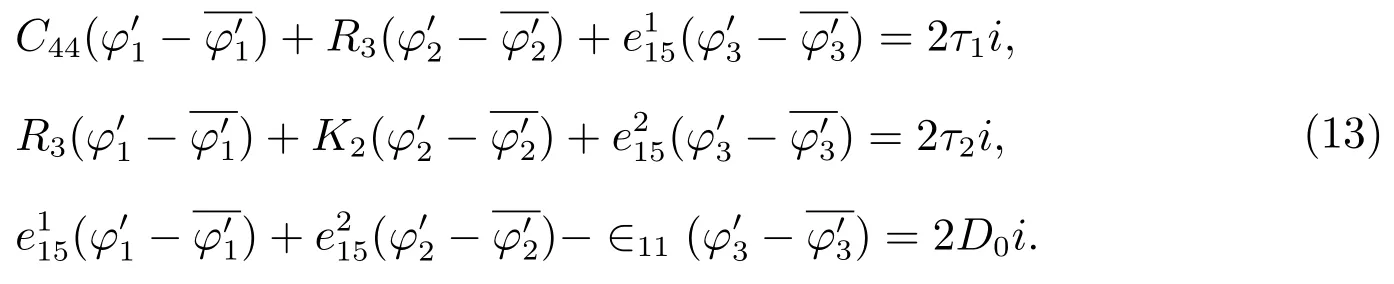
We propose the following conformal mapping:

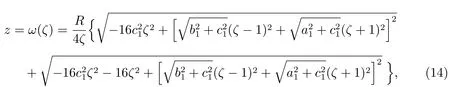
where

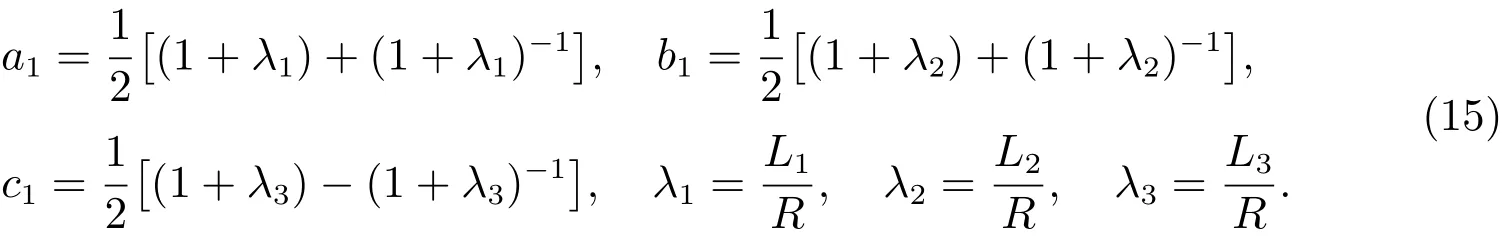
It can be shown that(14)provides a conformal mapping from the outsiDeregion of the hole and cracks in the physical plane to the interior of a unit circle in theζplane,and

We introduce the notationBy using the chain rule of derivative,we obtain

Substituting(16)into(13),then multiplying both sides of(13)bywhereζis an arbitrary point inand integrating around the unit circle Γ,we have

According to the Cauchy integral formula,one has

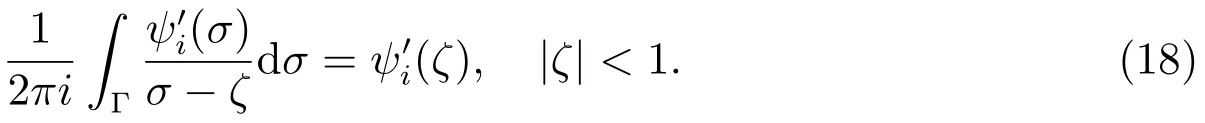
Differentiating(14)with respect toζleads to

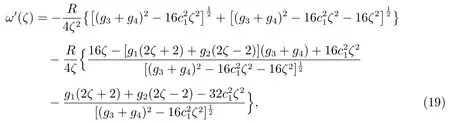
where

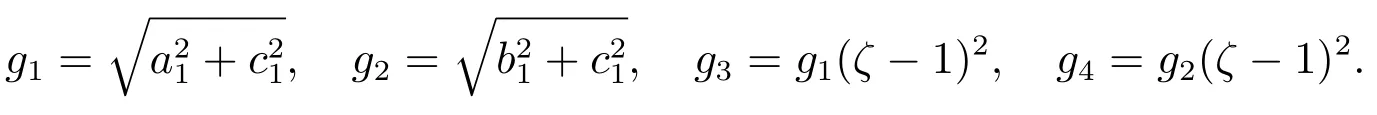
By(19),one has

From(19),it can be found thatis analytic inand continuous inHence,according to the Cauchy’s integral formula of infinite region,one finds

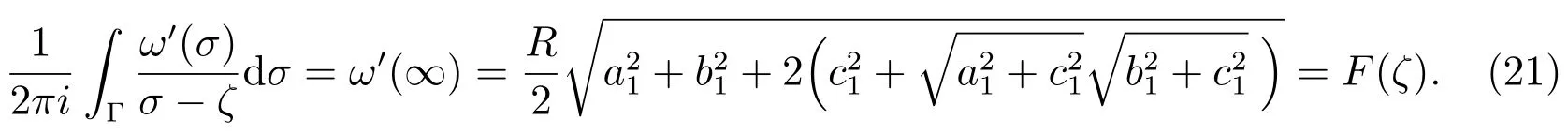
Sinceare analytic functions within the unit circle i.e.and(20),one has

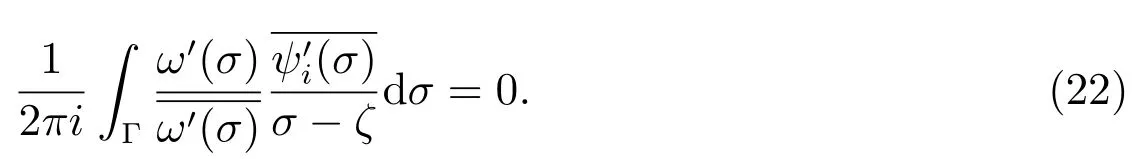
Substituting(18)and(21),(22)into(17),yields

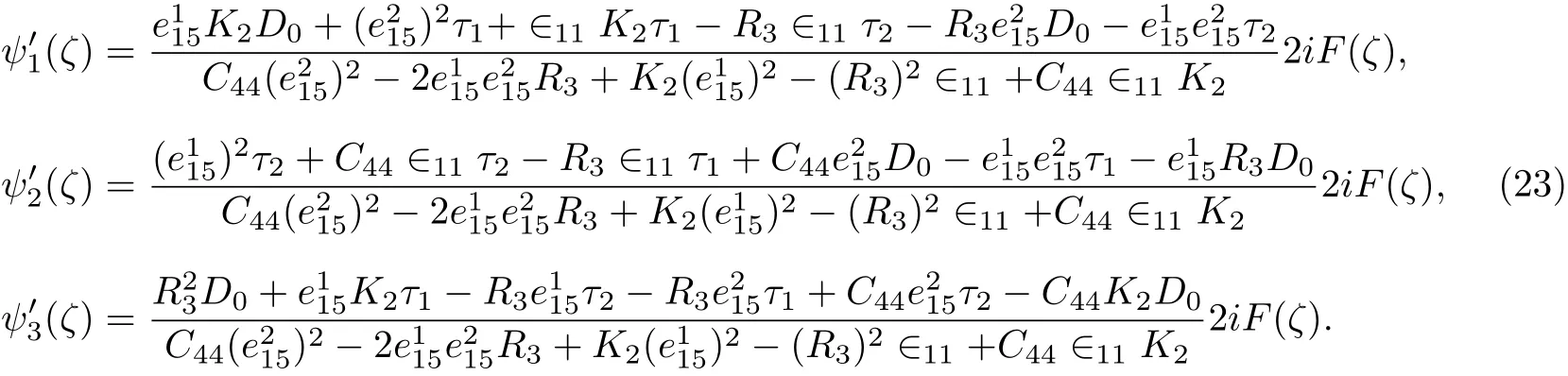
Substituting(23)into(12),we have

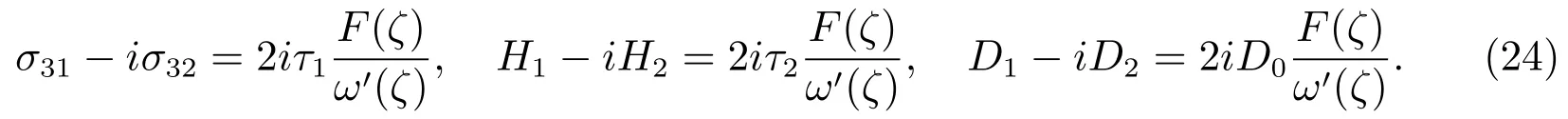
Then the stresses fields and the electric displacements can be determined,we omit them since the complexity of the expressions.

The vector of the SIFs of the phonon field and the phason field,and the EDIFs can be expressed in theζ-plane,as[8]

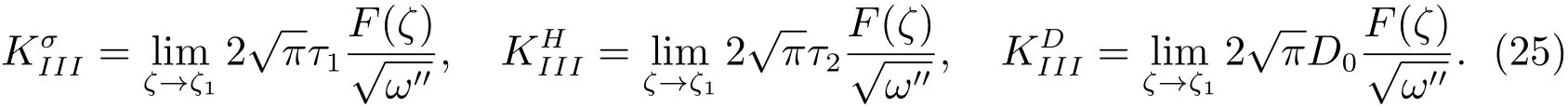
From(19)and(21),we have

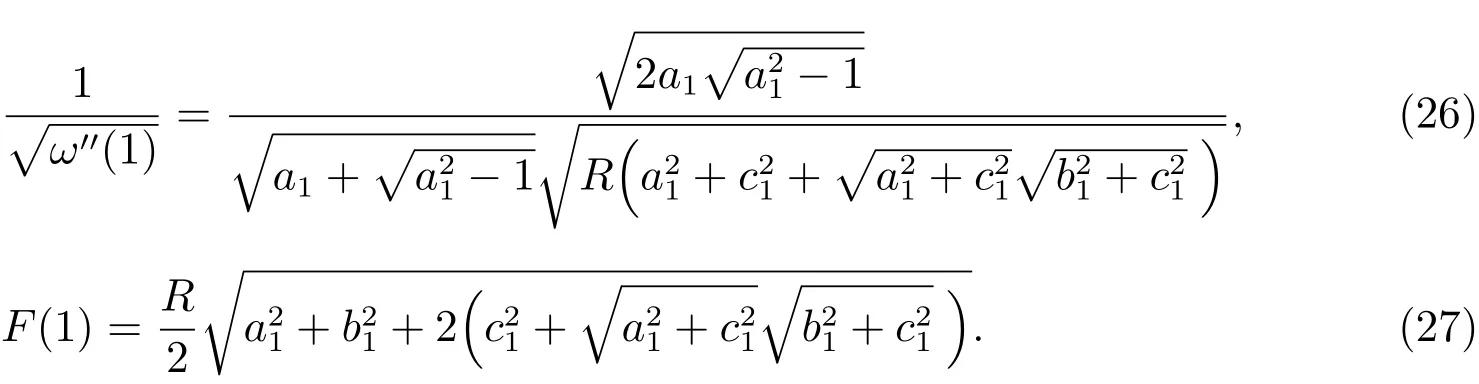
Substituting(26),(27)into(25),we obtain the SIFs of the phonon field and the

phason field,and EDIFs at the crack tipfor electric impermeable as follows

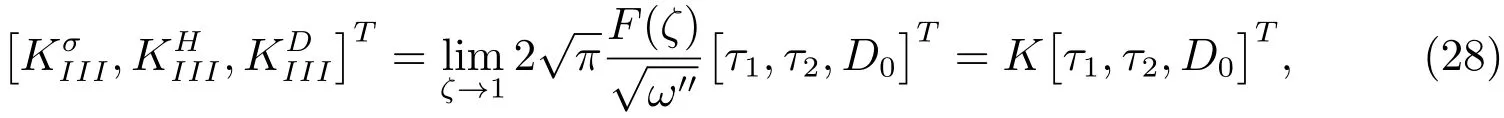
where

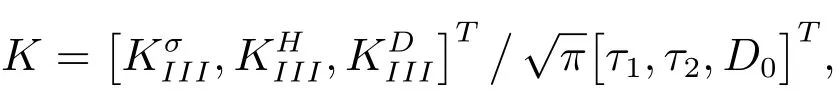
called for the dimensionless intensity factor,is defined as

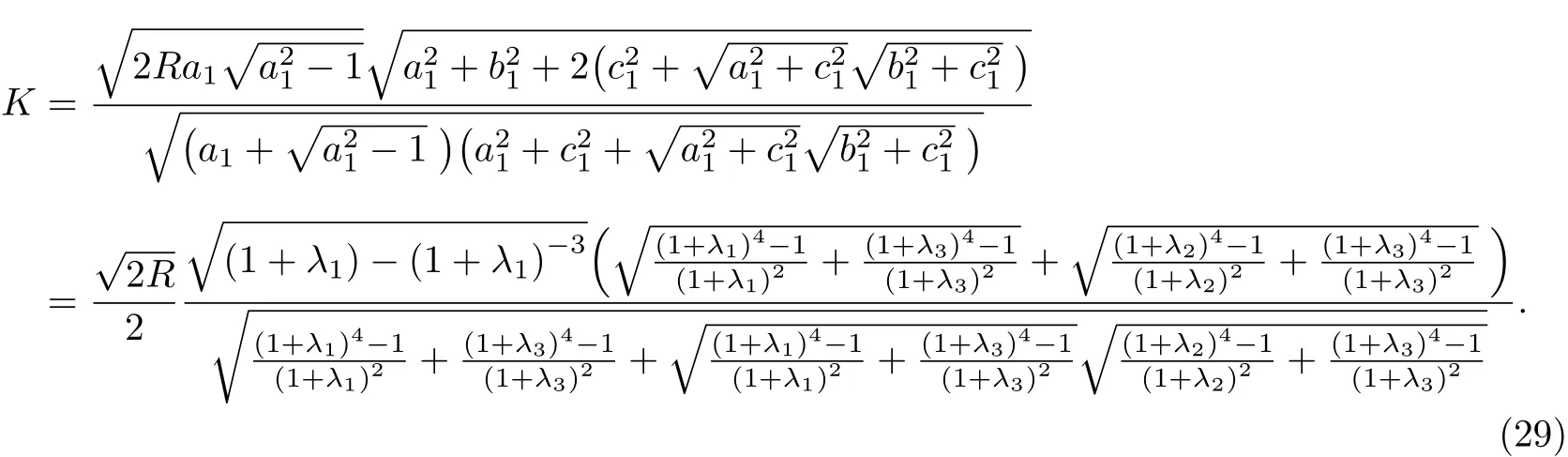
(28)shows that the field intensity factors of three unequal cracks emanating from a circular hole in 1D hexagonal piezoelectric quasicrystals are related to the phonon and phason stress,electric loading,and the dimensionless intensity factor asKas well.

When 1D hexagonal piezoelectric quasicrystals degenerated into 1D hexagonal quasicrystals,the SIFs of the phonon field and the phason field are these analytic solutions match with the result given in[18].

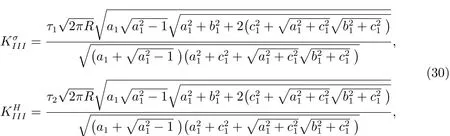
3.2 Electric permeable problem

The electric permeable boundary condition can be expressed as

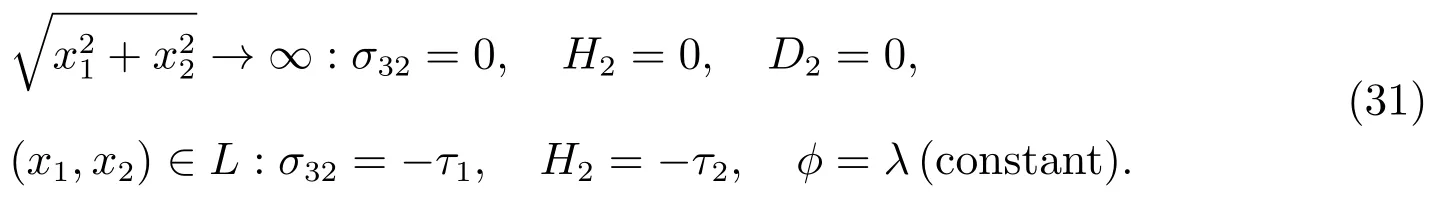
Substituting?=λinto(5)–(7),and applying(10),we have

Substituting(32)into(31),we obtain

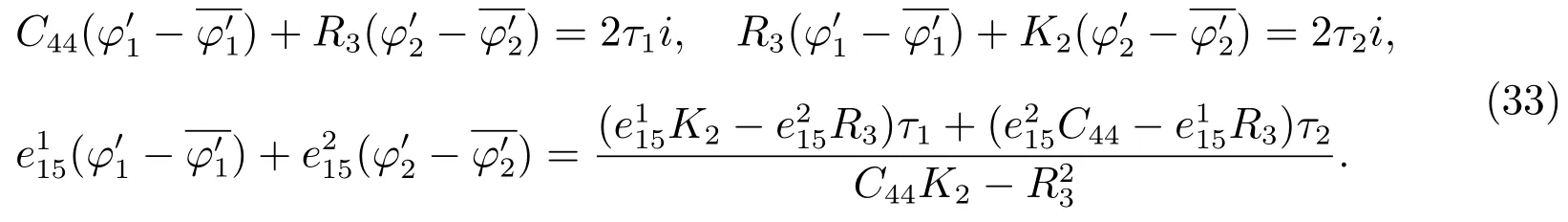
Similar to the electric impermeable derivation process,we have

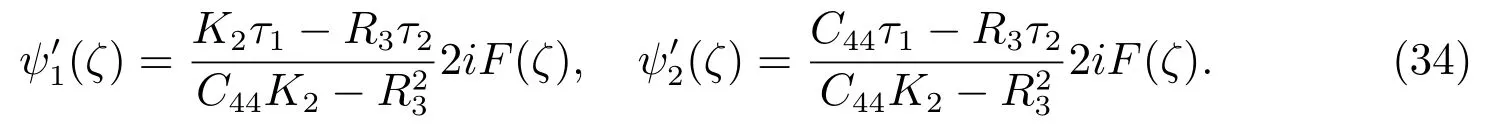
Similarly,one can obtain the stresses fields and the electric displacements for the permeable case.Because of the diffusive calculation,we neglect them here.

In the same way,the SIFs of phonon and phason fields,and the EDIFs for electric permeable can be obtained as follows

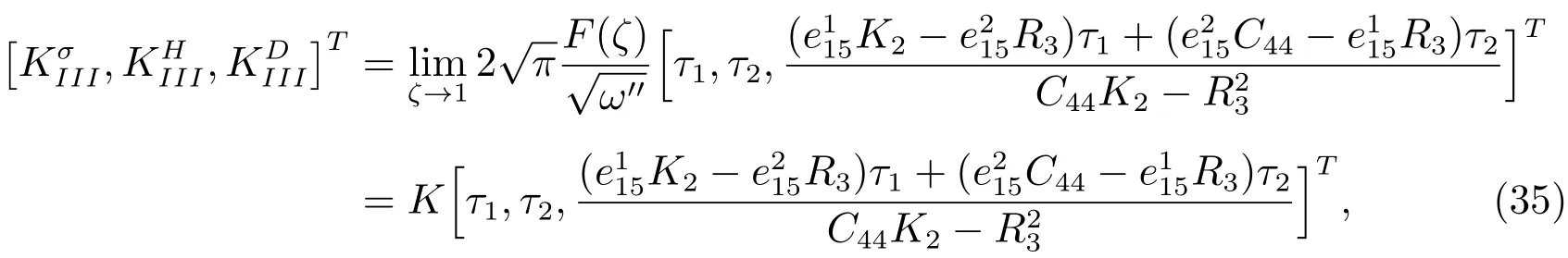
whereKis given by(29).

(35)indicates that for a permeable crack,the stress intensity factor relates to only the applied mechanical load,while the electric displacement intensity factor is induced by the piezoelectric effect.Furthermore,the electric displacement loading has no contribution to the stress intensity factor and the electric displacement intensity factor.The same conclusions for the permeable case in piezoelectric material are presented by the previous work[19].

4 Discussion and results

We have obtained the SIFs and the EDIFs of a circular hole with three unequal cracks in 1D hexagonal piezoelectric quasicrystals above.These results are discussed further as follows.

1)W hen the vertical crack lengthL3tends to zero,one has thatc1→0 from(15).In this case,(28)becomes

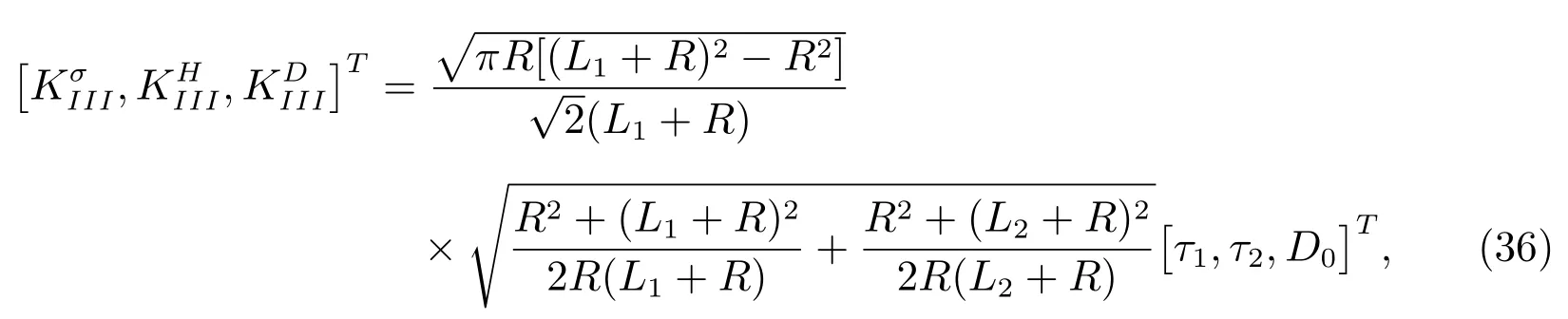
which denotes the result of two asymmetric cracks emanating from a circular hole in a 1D hexagonal piezoelectric quasicrystals.The SIFs of phonon and phason fields consist w ith[20]in the absence of the electric load.And in the absence of the phason field,which match with the result given in[21]fora=b.

2)Especially,when the horizontal crack lengthL2approaches toL1,then(36)produces

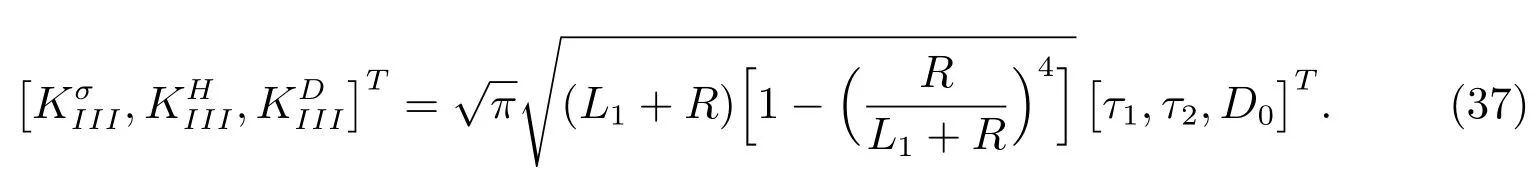
(37)represents result of a circular hole w ith two symmetric cracks in a 1D hexagonal piezoelectric quasicrystals.As far as the phonon field is concerned,which is identical to the corresponding result given by[22].As the phonon field and phason field are concerned,which agrees well w ith the result given in[23]fora=b.In the absence of the phason field,which are identical to the result given in[24]forn=2.

In particular,if the horizontal crack lengthL2tends to zero,then(37)reduces to the result of a circular hole w ith a straight crack in a 1D hexagonal piezoelectric quasicrystals,i.e.,

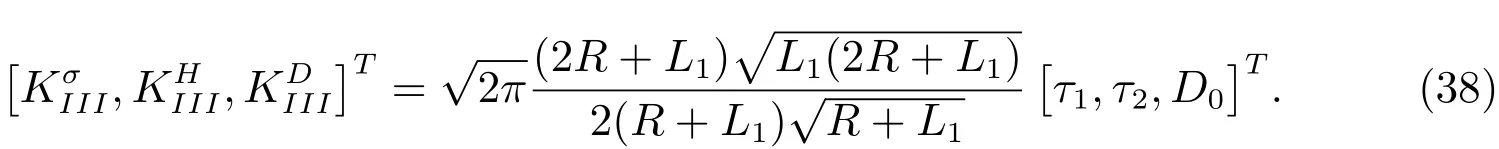
For the phonon field,(38)accords w ith those in[25].In the absence of the EDIFs,(38)matchs with the classical results[26].In the absence of the phason field,which match w ith the classical results[27].

3)If(38)leads to

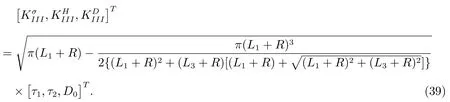
(39)gives the exact analytic solutions of the SIFs and the EDIFs of the modeLcrack in 1D hexagonal piezoelectric quasicrystals.In particular,whenL3→0,(39)produces

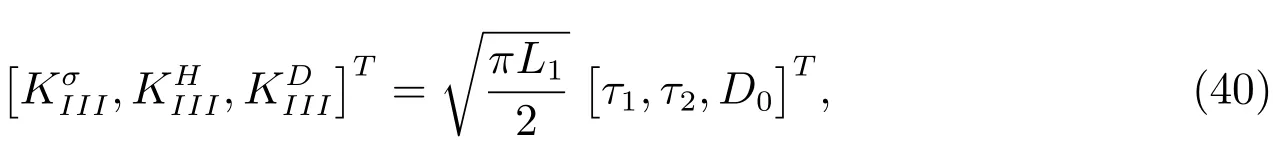
these are the result of the Griffith crack in a 1D hexagonal piezoelectric quasicrystals.As far as phonon field is concerned,which is identical to the results in[8].

5 Numerical examples

The dimensionless intensity factor,K,can be used to determine the field intensity factors of three edge cracks emanating from a circular hole.it can be seen from(29)that the dimensionless intensity factor is dependent on the radius of the circular hole as well as crack length.Introducing the dimensionless parametersL1/R,L2/RandL3/R(the ratio of crack length and radius)to represent crack size.The following numerical calculation to investigate the effect of geometric parameters on the dimensionless intensity factor.The numerical results are shown in Figure 2 to Figure 4.

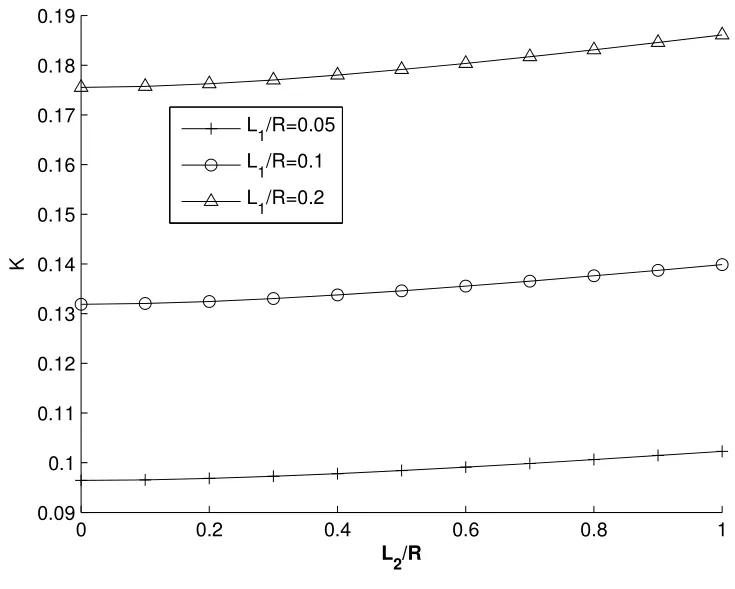
Figure2:Variations in K with L2/R for different L1/R

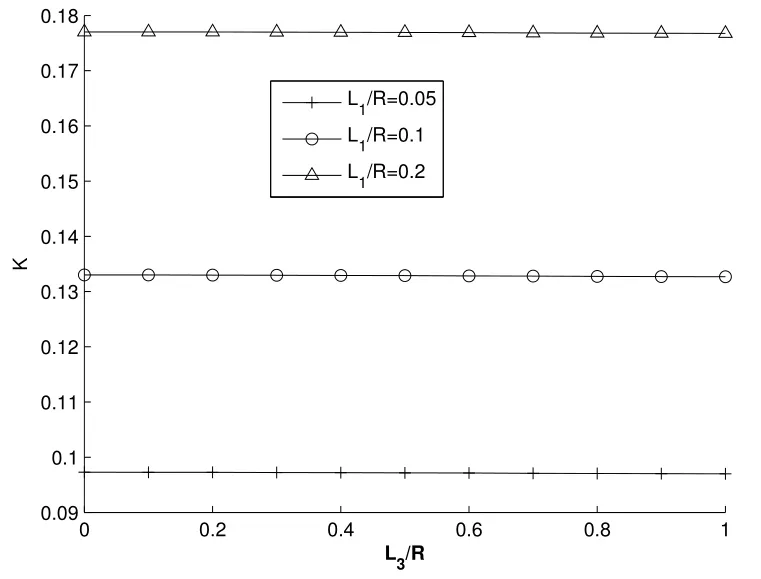
Figure 3:Variations in K with L3/R for different L1/R

The variations in the dimensionless intensity factorKversus the left crack lengthL2/Rfor different right crack lengthL1/Rare shown in Figure 2(L3/R=0.03,R=0.05).It is found that the value ofKincreases asL2/Rbecomes large,and then levels off.In addition,the value ofKalso increases as the right crack lengthL1/Rbecomes longer at a given left crack length.The result indicates that the increase of the right crack length easily promotes the failure of materials at given hole-size and the left crack length.

Figure3:displays the effect of the vertical crack lengthL3/Ron the dimensionless intensity factorKunder different right crack lengthL1/RwhereL2/R=0.03,R=0.05.It is shown that the influence ofL3/RtoKis not obvious.The results show that if the solid is shear loading and electric loading along the quasiperiodic direction(x3direction)at infinity,the influence of the crack parallel tox2axis toKis very small.

Figure4:demonstrates the effect of right crack lengthL1/Ron the dimensionless intensity factorKfor different the circle radiusR,whereL2/R=0.05,L3/R=0.03.It can be seen that in general cases,the value ofKincreases asRincreases,which indicates that the stress concentration around the crack tips may be relieved by adjusting the circle radius.

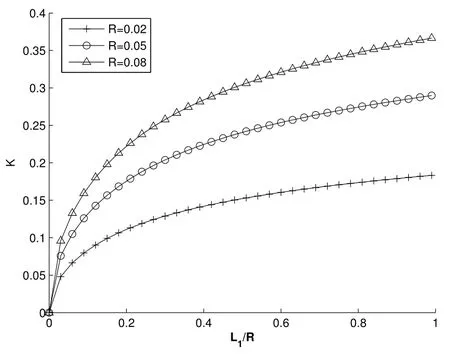
Figure4:Variations in K with L1/R for different R

6 Conclusion

Under the electric impermeable and electrical permeable boundary conditions,the anti-plane shear problem of a circle hole with three unequal cracks in 1D hexagonal piezoelectric quasicrystals is solved by means of complex variable function method with conformal mapping in this paper.The exact solutions of the SIFs for the phonon field and the phason field,and the EDIFs are obtained.These solutions are found for the first time in a 1D hexagonal piezoelectric quasicrystals and have signi ficance to the theory of brittle fracture of solids including quasicrystals.Under the electrical impermeable boundary condition,it is shown that the SIFs and the EDIFs does not occur coupling,and they have singularities at the crack tip.While the EDIFs is different from the previous results on the electrical permeable crack assumption,it depends on both material properties and the shear loads,but not the electric loads.In other words,the uniform electric loads have no in fluence on the field singularities.So,in fluence of theelectric load on defects cannot be ignored,electric load has played an accelerating role in the fracture of materials.Therefore,this research is necessary.With the variation of the hole-size and the crack lengths,the present results can be applied to stimulate many new crack configurations in practice,such as two asymmetric cracks,two symmetric cracks and a straight crack emanating from a circular hole,the modeLcrack and the Griffith crack,which are new and useful to theoretical researchers,in particular for the study of quasicrystals.

References:

[1]Dieulesaint E,Royer G A.Elastic Waves in Solids[M].New York:John Wiley & Sons,1980

[2]Rao S S,Sunar M.Piezoelectricity and its use in disturbance sensing and control of flexible structures:a survey[J].Applied Mechanics Review,1994,47(4):113-123

[3]Tsou H S,Bergman L A.Dynamics and Control of Distributed[M].Cambridge:Cambridge University Press,1998

[4]Uchino K.Materials issues in design and performance of piezoelectric actuators:an overview[J].Acta Materialia,1998,46(11):3745-3753

[5]Shechtman D,Blech I,Gratias D,et al.Metallic phase with long-range orientational order and no translational symmetry[J].Physical Review Letters,1984,53(20):1951-1953

[6]Meng X M,Tong B Y,Wu Y K.Mechanical properties of Al65 Cu20 Co15[J].Acta Metallurgica Sinica,1994,30(1):60-64

[7]Zhang Z,Urban K.Transmission electron microscope observation of dislocation and stackling faults in a decagonal Al-Cu-Co alloy[J].Philosophical Magazine Letters,1989,60(3):97-102

[8]Fan T Y.The Mathematical Theory of Elasticity of Quasicrystals and its Applications[M].Beijing:Science Press,2010

[9]Li X F,Fan T Y.A straight dislocation in one-dimensional hexagonal quasicrystals[J].Physica Status Solidi,1999,212(1):19-26

[10]Fan T Y,Li X F,Sun Y F.A moving screw dislocation in a one-dimensional hexagonal quasicrystals[J].Acta Physica Sinica(Overseas Edition),1999,8(4):288-295

[11]Muskhelishvili N I.Some basic Problem of the Mathematical Theory of Elasticity[M].Groningen:Noordhoff,1953

[12]Gao Y,Xu S P,Zhao B S.Boundary conditions for plate bending in one-dimensional hexagonal quasicrystals[J].Journal of Elasticity,2007,86(3):221-233

[13]Wang X,Pan E.Analytical solutions for some defect problems in 1D hexagonal and 2D octagonal quasicrystals[J].Journal of Physics,2008,70(5):911-933

[14]Guo J H,Lu Z X.Exact solution of four cracks originating from an elliptical hole in one-dimensional hexag-onal quasicrystals[J].Applied Mathematics and Computation,2011,217(22):9397-9403

[15]Wu Y F,Chen W Q,Li X Y.Indentation on one-dimensional hexagonal quasicrystals:general theory and complete exact solutions[J].Philosophical Magazine,2013,93(8):858-882

[16]Li X,Huo H S,Shi P P.Analytic solutions of two collinear fast propagating cracks in a symmetrical strip of one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Solid Mechanics,2014,35(2):1-7

[17]Yang J,Li X.Analytic solutions of problem about a circular hole with a straight crack in one-dimensional hexagonal quasicrystals with piezoelectric effects[J].Theoretical and Applied Fracture Mechanics,2015,doi:10.1016/j.tafmec.2015.07.012

[18]Yang L Y.The complex variable function method research on the problem of complicated defects of classical elasticity and quasicrystals[D].Huhhot:Inner Mongolia Normal University,2010

[19]Zhang T Y,Gao C F.Fracture behaviors of piezoelectric materials[J].Theoretical and Applied Fracture Mechanics,2004,41(1-3):339-379

[20]Guo J H,Liu G T.Analytic solutions of the one-dimensional hexagonal quasicrystals about problem of a circular hole with asymmetry cracks[J].Acta Mathematicae Applicatae Sinica,2007,30(6):1066-1075

[21]Guo J H,Lu Z X,Han H T,et al.Exact solutions for anti-plane problem of two asymmetrical edge cracks emanating from an elliptical hole in a piezoelectric material[J].International Journal of Solids and Structures,2009,46(21):3799-3809

[22]Sih G C.Stress distribution near internal crack tips for longitudinal shear problems[J].ASME,Journal of Applied Mechanics,1965,32(1):51-58

[23]Guo J H,Liu G T.Analytic solutions to problem of elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals[J].Applied Mathematics and Mechanics,2008,29(4):485-493

[24]Guo J H,Lu Z X,Feng X.The fracture behavior of multiple cracks emanating from a circular hole in piezoelectric materials[J].Acta Mechanica,2010,215(1-4):119-134

[25]Yang J,Li X.Analytic solutions of the anti-plane problems about a circular hole with a crack[J].Mathematics in Practice and Theory,2014,44(21):245-249

[26]Ma G Y,Guo H M.Analytic solutions of problem about an circular hole with a straight crack in onedimensional hexagonal quasicrystals[J].Yinshan Academic Journal,2010,24(4):5-15

[27]Wang Y J,Gao C F.The moDeIII cracks originating from the edge of a circular hole in a piezoelectric solid[J].International Journal of Solids and Struct,2008,45(16):4590-4599