Fuzzy Robust H∞ Control for Uncertain Nonlinear Systems via Output Feedback?
1 Introduction
Fuzzy Takagi-Sugeno(T-S)model is an effective tool to deal with nonlinear systems,because it is a good representation for a wide class of nonlinear dynamic systems[1].By now,the stability analysis and control design for many various systems have been wide ly discussed.
As usual,the approximation error(the uncertainties)between nonlinear system and fuzzy T-S model is ignored.To avoid the effect of the approximation error,a matching condition is assumed in[2],and an upper bound on the approximation error isintroduced in[3],on the other hand,fuzzy logic systems can be used to deal with the uncertainties in[4].
Based on the above discussions,we propose a novel robustH∞control scheme for a class of uncertain nonlinear systems represented in fuzzy T-S form.A fuzzy observer is designed to observe the system states,with which a fuzzy output feedback controller is designed to guarantee the stability of the fuzzy system.A compensator based fuzzy logic systems is introduced to eliminate the uncertainties.Applying Lyapunov stability theorem,the proposed fuzzy control scheme ensures that the desiredH∞performance is achieved in the sense that all the closed-loop signals uniformly are ultimately bounded(UUB).Simulation results demonstrate the effectiveness and the superiority of the developed control scheme.
2 Problem formulation
Consider the following uncertain nonlinear systems
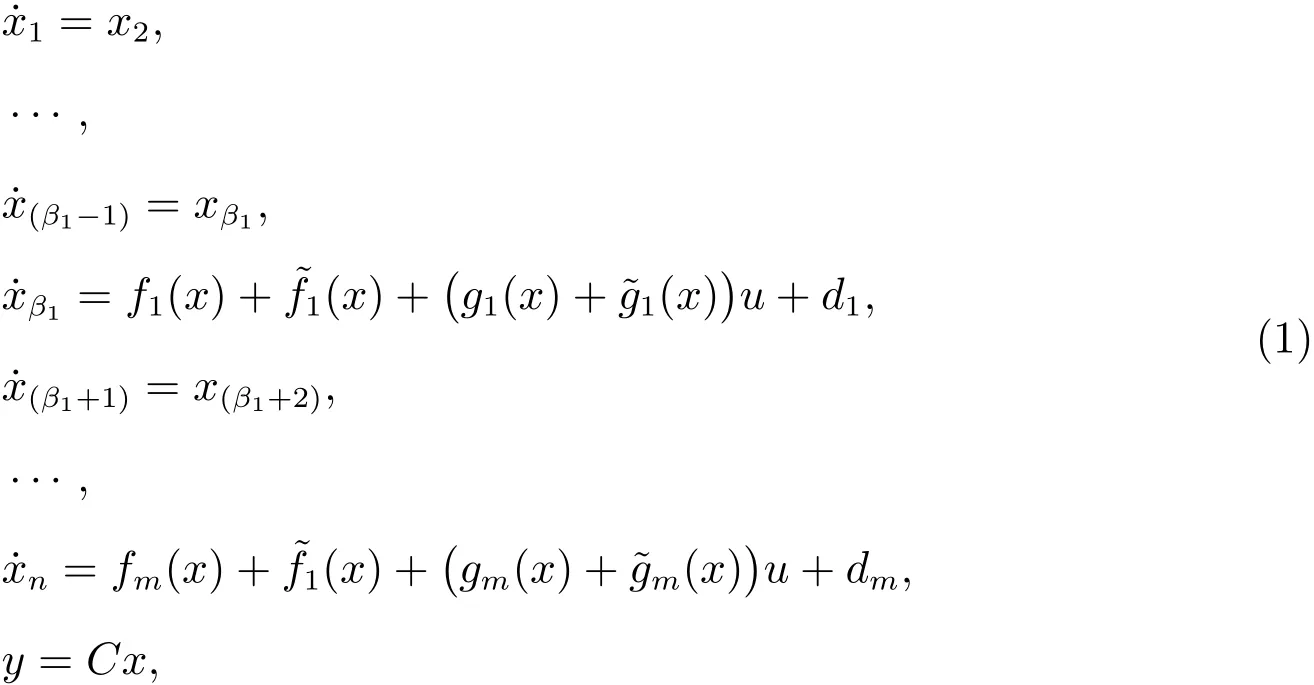
wherex,uandyare the system state,control input,and system output,respectively;xis assumed to be unavailable.is a constant matrix,are smooth nonlinear functions,andare unknown uncertain functions,anddenotes external disturbances.
The control objective of this paper is to find a fuzzy robustH∞controller such that the desiredH∞performance is achieved.
3 Fuzzy model,fuzzy observer and fuzzy controller
A fuzzy control system with a fuzzy model,a fuzzy observer,and fuzzy controller connected in a closed-loop is given.
3.1 Fuzzy model
The dynamic behavior of the nonlinear system(1)can be represented by fuzzy T-S model
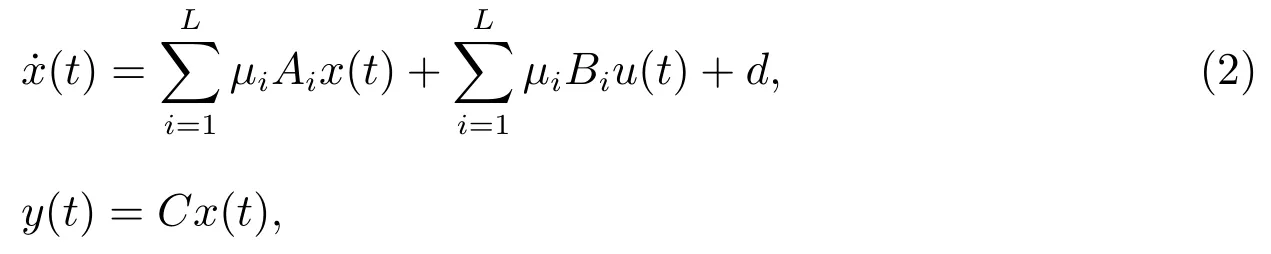
where
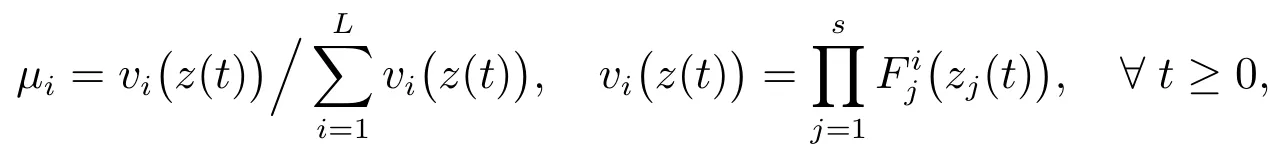
andis the graDeof membership ofzj(t)inSupposing that
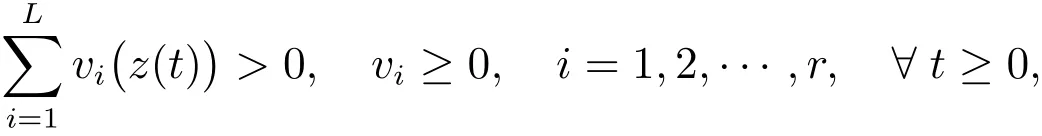
we have
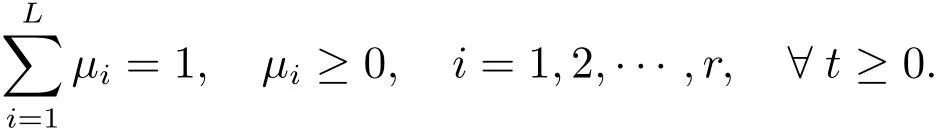
Finally,the nonlinear system(1)is equivalent to the following system
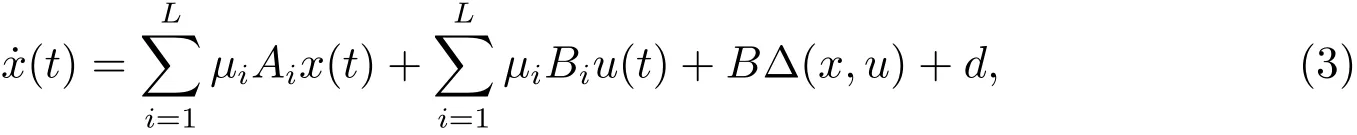

wheredenotes the approximation error,which is uncertain,and
3.2 Fuzzy observer
Owing to the unavailability of the system states,a fuzzy observer is designed to estimate the system statesx(t).The overall fuzzy observer is given as follows
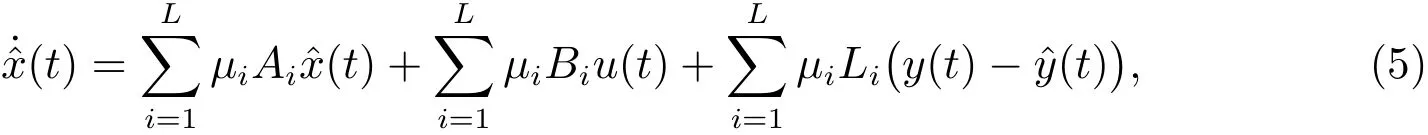

wherethe appropriate matrix.
3.3 Fuzzy controller
We design the following fuzzy controller

whereul(t)is a fuzzy output feedback controller based on T-S model,anduf(t)denotes an adaptive output feedback compensator based on fuzzy logic systems.
For the fuzzy model(2),the overall output feedback controllerul(t)is given by

in whichis the appropriate matrix and satisfies the following inequalities
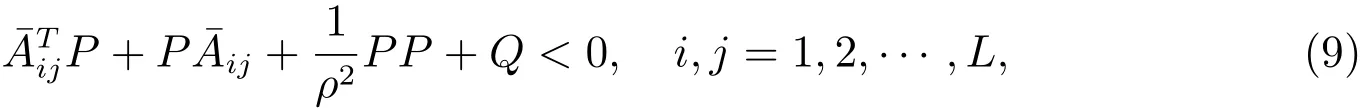
where

P1,P2,Q1andQ2are some symmetric and positive definite matrices,andρis a positive constant.
The adaptive compensator based on fuzzy logic systemsuf(t)is designed as follows
where
andis constructed by fuzzy logic systems.The weightis an adaptive parameter,which is adapted by

whereη1is a positive constantis the output error of the system,is a fuzzy basis-function matrix.Fuzzy logic systems are constructed to approximate the modeling errorwith the following form:Denote the estimation errorThen,the approximation error for the functioncan be expressed as
whereis a residual term.
4 Stability analysis
By using(5)–(8)and(10),we obtain
where
By use of(3)–(8)and(10),a new extended closed-loop system is as follows

where
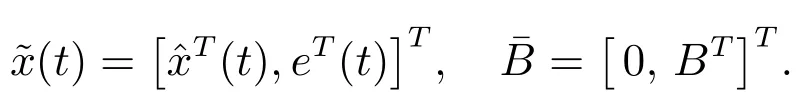
Substituting(12)into(14)yields
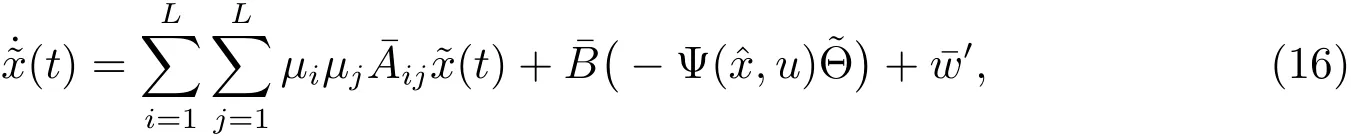

where
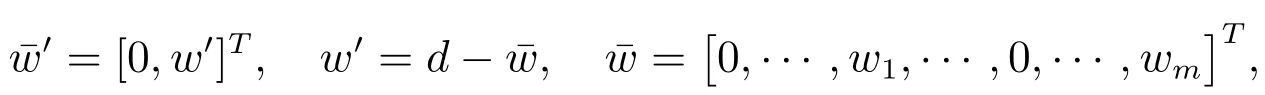
andP2,B,Csatisfy

From the above analysis,we have the following conclusion.
TheoremAssume that the symmetric and positive definite matricesPandQ,and a positive scalarρsatisfy the inequalities(9),and the updating law for the parameter is selectd as(11).Then there exists a controller(7)composed of(8)and(10)such that theH∞performance is achieved in the sense that all the closed-loop signals are UUB.
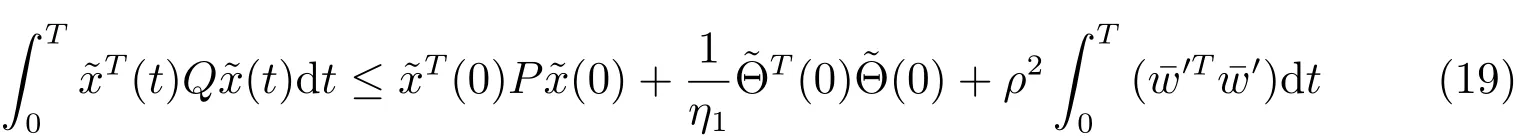
5 Simulation example
In this section,an example is provided to verify the effectiveness of the proposed control scheme.
ExampleConsider the following rotated inverted pendulum system in[5]
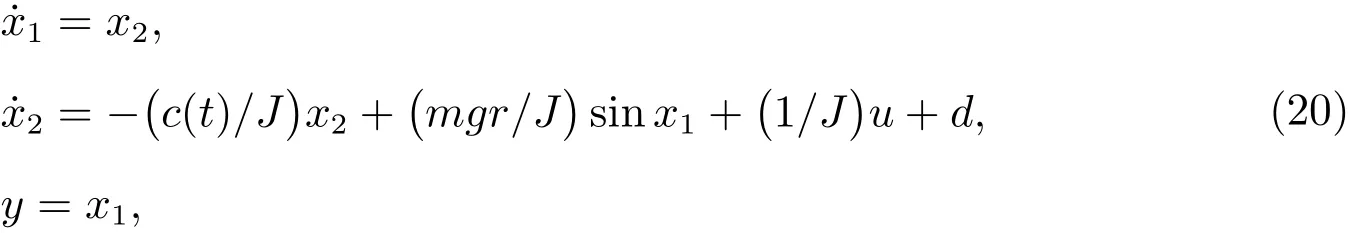
whereJdenotes the inertia of the motor and the load,dis the external bounded disturbance,andc(t)is uncertain and bounded.
By using the method in Theorem,we can design the controller and simulation results are shown in Figure 1.
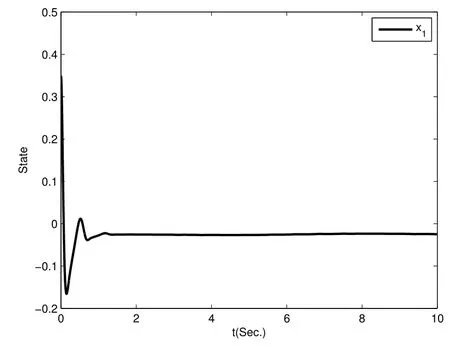
Figure1:State response of x1
6 Conclusion
In this paper,a novel fuzzy output-feedback control scheme is presented.Next,this method could be extended to discrete systems,stochastic systems and time-variant systems,etc.
References:
[1]Takagi T,Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Transactions on Systems,Man,and Cybernetics,1985,SMC-15(1):116-132
[2]Yoneyama J.Robust sampled-data stabilization of uncertain fuzzy systems via input delay approach[J].Information Sciences,2012,198(1):169-176
[3]Lien C H,Chen J D,Yu K W,et al.Robust delay-dependentH∞control for uncertain switched time-delay systems via sampled-data state feedback input[J].Computers & Mathematics with Applications,2012,64(5):1187-1196
[4]Wang L X.Stable adaptive fuzzy control of nonlinear systems[J].IEEE Transactions on Fuzzy Systems,1993,1(2):146-155
[5]Liu Y,Hu S S.Fuzzy robust tracking control for uncertain nonlinear systems[J].Acta Automatica Sinica,2004,30(6):948-953
- 工程數(shù)學(xué)學(xué)報的其它文章
- Oscillation Criteria for Third-order Nonlinear Neutral Dynamic Equations on Time Scales?
- Anti-plane Analysis of a Circular Hole with Three Unequal Cracks in One-dimensional Hexagonal Piezoelectric Quasicrystals?
- 一類具有非線性發(fā)生率的SEIR傳染病模型的全局穩(wěn)定性分析?
- 非奇異H-矩陣的一組判定條件?
- 基于Brown構(gòu)形場方法的二維收縮流模擬?
- 一個具有時滯和階段結(jié)構(gòu)的比率依賴型捕食系統(tǒng)的穩(wěn)定性?

