雙曲空間形式中的全臍超曲面與高階平均曲率

王琪

(貴陽學院數(shù)學與信息科學學院,貴州貴陽550005)

雙曲空間形式中的全臍超曲面與高階平均曲率

王琪

(貴陽學院數(shù)學與信息科學學院,貴州貴陽550005)

本文研究了雙曲空間形式中等距浸入的緊致無邊超曲面的全臍性質(zhì)和高階平均曲率.利用高階平均曲率積分估計的方法,獲得了一個新的定理,改進了這個研究方向上有關(guān)的最近結(jié)果.

全臍超曲面;高階平均曲率;雙曲空間形式

1 引言和結(jié)果

Biven[1]研究了雙曲空間形式中的超曲面,得到用高階平均曲率刻畫超曲面全臍性質(zhì)的曲率條件,即下列定理1.1.

隨后,Sung Eun Koh[2]減弱對高階平均曲率的限制條件,改進文[1]的結(jié)果,得到下列定理1.2.

最近,王琪[3]進一步減弱對高階平均曲率的限制,在外圍空間為正曲率空間形式的情形,得到下列定理1.3,對這個研究方向作出進一步的改進.

本文討論雙曲空間形式中的超曲面,在外圍空間是雙曲空間形式的情形,得到一個與定理1.3類似的定理,即下列定理1.4.

定理1.1[1]設Mn是雙曲空間形式Hn+1中緊致無邊等距浸入超曲面.若對某個整數(shù)r(2≤r≤n)而言,高階平均曲率Hr-1和Hr在Mn上均為常數(shù),則Mn必是全臍的.

定理1.2[2]設Mn是雙曲空間形式Hn+1中緊致無邊等距浸入超曲面.若對某個整數(shù)r(2≤r≤n),高階平均曲率Hr-1處處非零且在Mn上為常數(shù),則Mn必是全臍的.

定理1.3[3]設Mn是球面Sn+1(c)(c＞0)中緊致無邊的等距浸入超曲面且Mn落在Sn+1(c)的一個開半球內(nèi).若存在兩個整數(shù)使得Hr處處非零且為常數(shù),則Mn必是全臍的.

定理1.4設Mn是雙曲空間形式Hn+1中緊致無邊等距浸入超曲面.若存在兩個整數(shù)使得Hr處處非零且為常數(shù),則Mn必是全臍的.

2 準備和引理

設Mn是n維黎曼流形,它等距浸入(n+1)維黎曼流形Nn+1中,即Mn是Nn+1中的超曲面.記Mn的主曲率函數(shù)為λi(1≤i≤n),則Mn的第r個高階平均曲率

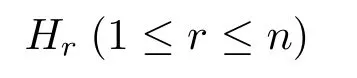
定義為[1-3,5-6]

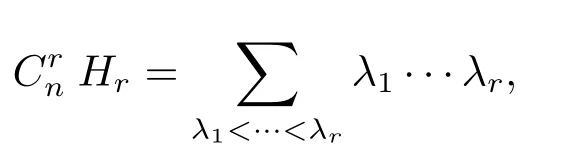
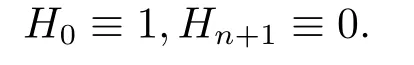
設Hn+1是(n+1)維單連通完備黎曼流形,且有常數(shù)截面曲率K≡-1,則Hn+1稱為雙曲空間形式.本文采用Hn+1的上半空間模型[1-2].

本文需要以下幾個引理.

引理2.1[1-2]設Mn是雙曲空間形式Hn+1中等距浸入緊致無邊超曲面,則Mn必有橢圓點.

引理2.2[1-2]若對某個整數(shù)r(1≤r≤n)而言,Hr＞0在Mn上成立,則對一切k=0,1,2,···,r必有Hk＞0在Mn上成立.

引理2.3[1-4]對一切r=1,2,···,n必有

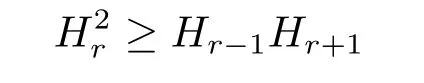
在Mn上處處成立.又對1≤r≤n-1而言,不等式在且僅在臍點處取等號.

引理2.4[1-2]設Mn是雙曲空間形式Hn+1中緊致無邊等距浸入超曲面.用x表示Mn典型嵌入在Rn+2中的位置向量,η表示Mn的單位法向量場.則對k=1,2,···,n有下列推廣的Minkowski積分公式

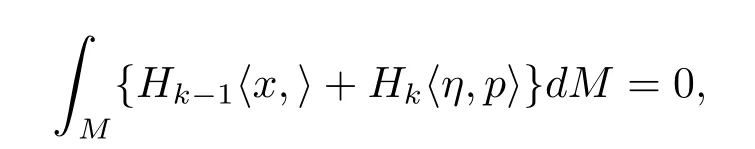
其中p∈Rn+2為任意固定向量,而dM表示黎曼流形Mn的體積元,〈.,.〉表示Rn+2中的Lorentz內(nèi)積.

3 定理1.4的證明

首先,無妨設s＜r.

由引理2.1,Mn必有橢圓點,故在該點處Hr和Hs均為正值,從而常數(shù)a=是正數(shù).因為假設Hr在Mn上處處非零,從而Hr＞0在Mn上處處成立,于是從引理2.2,對k=0,1,2,···,r有Hk＞0在Mn上處處成立,所以從引理2.3有

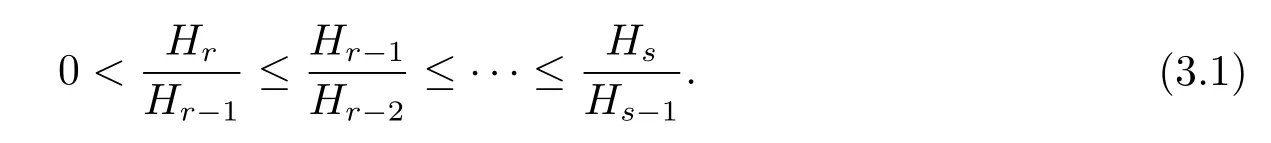
由引理2.4,可以寫以下兩個公式

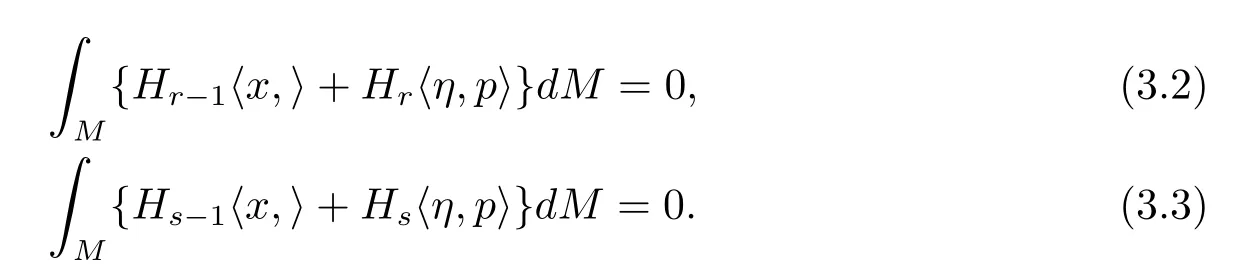
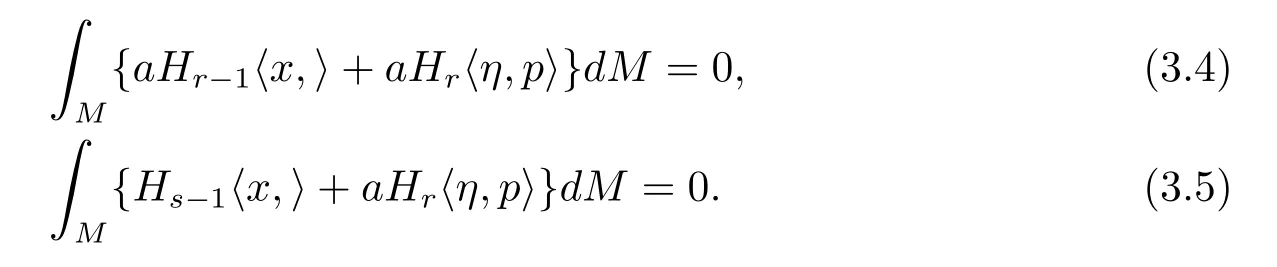
現(xiàn)在,從(3.4)式和(3.5)式立即寫下

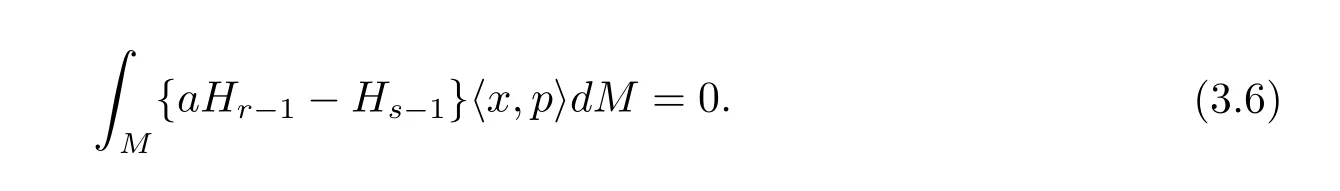
注意到(3.1)式,事實上在Mn上恒有

引理2.4的積分公式中的向量p∈Rn+2是可以任意取定的,并且Hn+1是典型嵌入在Rn+2的上半空間中,故可以適當選定p∈Rn+2使得下式成立

至此,由(3.6)、(3.7)和(3.8)式,在Mn上恒有

再由(3.1)式和(3.9)式,在Mn上恒有

最后,從(3.10)式及引理2.3立即知道,Mn是全臍的.

[1]Bivens I.Integral formulas and hypersurfaces in a simply connected space form[J].Proc.Amer. Math.Soc.,1983,88(1):113–118.

[2]Koh Sung-Eun.A characterization of round spheres[J].Proc.Amer.Math.Soc.,1998,126(12): 3557–3660.

[3]王琪.正曲率空間形式中超曲面的全臍性與高階平均曲率[J].數(shù)學學報,2014,57(1):47–50.

[4]Beckenbach E F,Bellman R.Inequalities[M].Berlin:Spring-Verlag,1971.

[5]韓英波,馮書香.雙曲空間Hn+1(-1)中完備超曲面(英文)[J].數(shù)學雜志,2013,33(5):10–15.

[6]韓英波,馮書香.雙曲空間形式中具有常平均曲率的超曲面(英文)[J].數(shù)學雜志,2014,34(4):34–40.

TOTALLY UMBILICAL HYPERSURFACES IN THE HYPERBOLA SPACE FORM AND HIGHER ORDER MEAN CURVATURES

WANG Qi
(School of Mathematics and Information Science,Guiyang University,Guiyang 550005,China)

In this paper,we study the totally umbilical property of hyper-surfaces in the hyperbola space form and higher order mean curvatures.Under a weaker condition on higher mean curvatures,we give a new theorem to improve and generalize some recent results in the research field.

totally umbilical hyper-surface;higher order mean curvature;hyperbola space form

tion:53C20;53C40

O186.17

A

0255-7797(2017)01-0211-04

2014-06-16接收日期:2014-12-02

貴州省科學技術(shù)基金資助(黔科合J字[2014]2005);貴州省科學技術(shù)基金資助(黔科合J字LKG[2013]31).

王琪(1963–),男,湖南雙峰,教授,主要研究方向:微分幾何.