小區(qū)間上特定類型的三角和估計(jì)

趙曉東

(華北水利水電大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,河南 鄭州 450046)

小區(qū)間上特定類型的三角和估計(jì)

趙曉東

(華北水利水電大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,河南 鄭州 450046)

利用Vaughan的方法,對小區(qū)間上的三角和

當(dāng)α為有理數(shù)時(shí)進(jìn)行了研究,得到了一個(gè)定量上界估計(jì).

三角和;小區(qū)間;有理數(shù);定量估計(jì)

1 引言及主要結(jié)果

形如

的三角和的估計(jì)在解析數(shù)論中有著很多應(yīng)用.例如在哥德巴赫猜想、素變數(shù)三角和的估計(jì)及素?cái)?shù)分布[14]等方面有著重要應(yīng)用.設(shè)實(shí)數(shù)

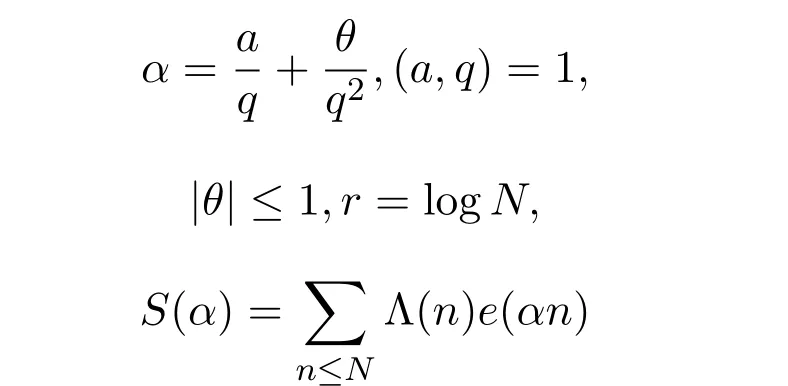
其中 Λ(n)為 Mangoldt函數(shù),e(αn)=e2πiαn,N ≥ 3是一個(gè)整數(shù).

1994年,陳景潤和王天澤[5]利用文獻(xiàn)[6]中的分拆方法,得到如下定量結(jié)果：

2013年,文獻(xiàn)[8]在上述基礎(chǔ)上討論了α為有理數(shù)的情形.

2015年,文獻(xiàn)[9]討論了當(dāng)x-y＜n≤x時(shí),S(α)的定量估計(jì),得到如下定量估計(jì)：

其中x,y是整數(shù),其他符號參照上述定義,則有

本文討論了在x-y＜n≤x上,α為有理數(shù)時(shí),S(α)的定量估計(jì),得到了如下結(jié)果：

定理1.1設(shè)α為有理數(shù)

N≥3是一個(gè)整數(shù).整數(shù)x,y滿足

記

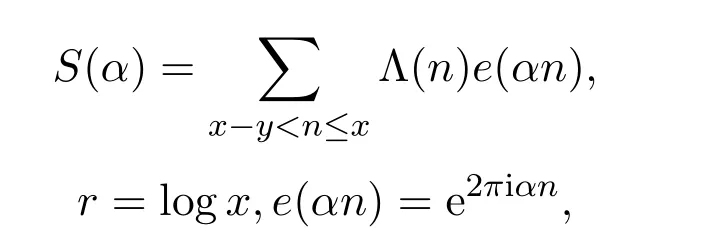
其中Λ(n)為Mangoldt函數(shù),則有

2 引理及簡單說明

引理 2.1[7]對任意整數(shù)N2≥N1≥1及實(shí)數(shù)α有,

其中

(α)是α的小數(shù)部分.

證明見文獻(xiàn)[7].

引理 2.2設(shè)U＞0是實(shí)數(shù),P≥1,M 是整數(shù),有理數(shù)滿足(a,q)=1,則有

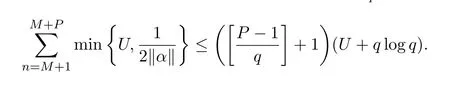
證明結(jié)合文獻(xiàn)[7-8].

引理2.3設(shè)α為有理數(shù),(a,q)=1.T≥1,N≥1都是實(shí)數(shù),則有

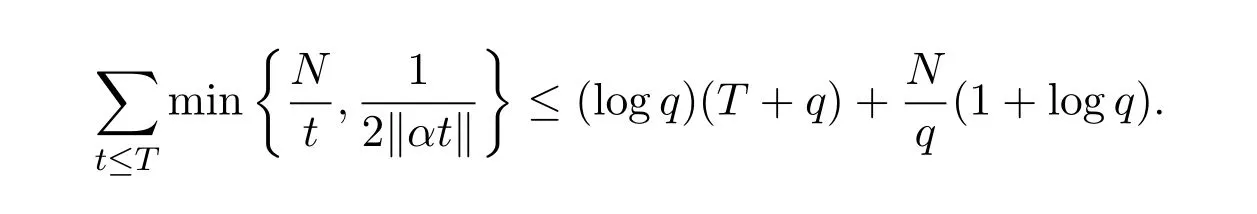
證明結(jié)合引理2.2及文獻(xiàn)[8].

3 定理1.1的證明

易知

當(dāng)

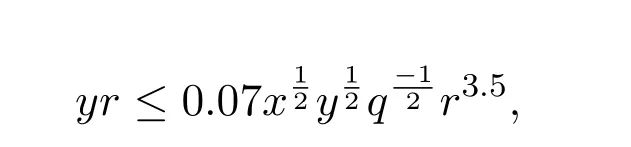
即 q≤0.005xy?1r5時(shí)結(jié)論成立,所以不妨設(shè)q≥0.01r5.同理,當(dāng)

在上述條件限制下,來確定S1,S2,S3,S4的上界估計(jì).由Λ(n)的定義可知：

在 S2中,令 w=ml,則

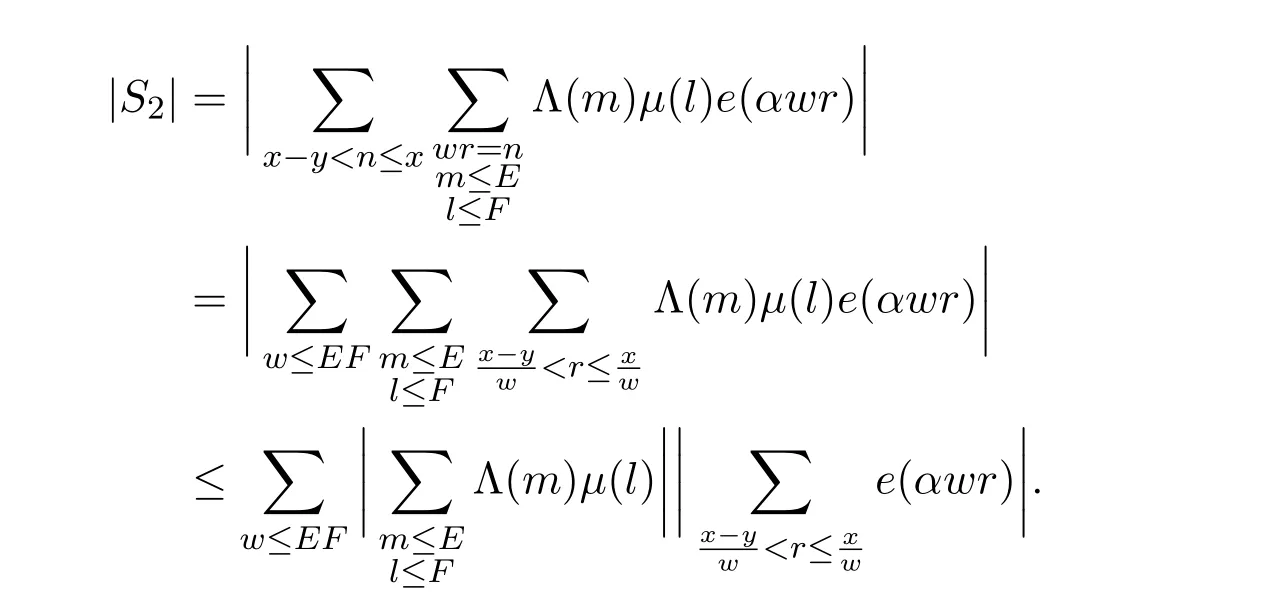
由引理2.1和引理2.3可知：

關(guān)于S3,

參考文獻(xiàn)

[1]劉建亞,呂廣世,展?jié)?小區(qū)間上的素變數(shù)三角和[J].中國科學(xué)：自然科學(xué)版,2006,4(8)：448-457.

[2]呂廣世.小區(qū)間上的素變數(shù)三角和的估計(jì)[J].數(shù)學(xué)學(xué)報(bào),2006,3(27)：693-698.

[3]Karatsuba A A.Basic Analytic Number Theory[M].New York：Springer-Verlag,1993.

[4]Vaughan R C.The Hardy-Littlewood Method[M].London：Cambridge,1997.

[5]王天澤,陳景潤.素變數(shù)線性三角和的估計(jì)[J].數(shù)學(xué)學(xué)報(bào),1994,1(37)：25-31.

[6]Davenport H.Multiplicative Number Theory[M].New York：Springer-Verlag,1980.

[7]陳景潤.某種三角和的估計(jì)及應(yīng)用[J].中國科學(xué)：自然科學(xué)版,1984,12(27)：1096-1103.

[8]陳國華,武艷麗,張艷娜.某種特定類型三角和的定量估計(jì)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2013,29(3)：325-330.

[9]戈文旭,趙峰.小區(qū)間上某種三角和的估計(jì)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2015,31(3)：260-264.

On estimation of a speci fi c type trigonometrical sums in small interval

Zhao Xiaodong
(School of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450046,China)

By the method of vaughan,the problem of the estimate of

is studied,when α is rational,and obtain an explicit upper bound of this kind of trigonometrical sums.

trigonometrical sums,small interval,rational,explicit estimate

O156.4

A

1008-5513(2017)04-0370-07

10.3969/j.issn.1008-5513.2017.04.005

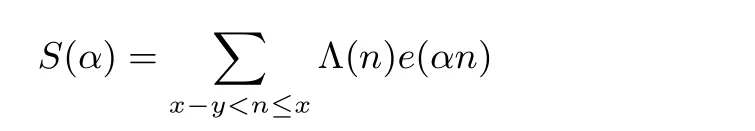
2017-05-08.

趙曉東(1991-),碩士生,研究方向：數(shù)論.

2010 MSC:11L03