安徽省碭山中學(xué)(235300)蓋傳敏

周期數(shù)列的定義對(duì)于數(shù)列{an},若存在正整數(shù)T,使得對(duì)于任意正整數(shù)n,都有an+T=an,則稱(chēng)數(shù)列{an}為周期數(shù)列.其最小正周期記為T(mén).

結(jié)論1在數(shù)列中{an},若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有an+k=-an,則數(shù)列{an}是周期為2k的周期數(shù)列.

證明因?yàn)閍n+2k=-an+k=an,所以數(shù)列{an}是周期為2k的周期數(shù)列.

結(jié)論2在數(shù)列{an}(an/=0)中,若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有則數(shù)列{an}是周期為2k的周期數(shù)列.

證明因?yàn)樗詳?shù)列{an}是周期為的周期數(shù)列.

結(jié)論3在數(shù)列{an}(an/=0)中,若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有則數(shù)列{an}是周期為2k的周期數(shù)列.

證明因?yàn)樗詳?shù)列{an}是周期為的周期數(shù)列.

結(jié)論4在數(shù)列{an}中,若存在正整數(shù)k,使得對(duì)于正整數(shù)n(n＞k),都有an=an-k+an+k(n＞k),則數(shù)列{an}是周期為6k的周期數(shù)列.

證明由

可得

①式加②式可得an+2k=-an-k(n＞k),即an+3k=-an(n∈N+).由結(jié)論1可知數(shù)列{an}是周期為6k的周期數(shù)列.

結(jié)論5在數(shù)列{an}(an/=0)中,若存在正整數(shù)k,使得對(duì)于正整數(shù)n(n＞k),都有an=an-k·an+k(n＞k),則數(shù)列{an}是周期為6k的周期數(shù)列.

證明由

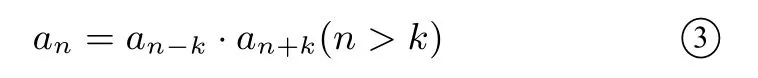
可得

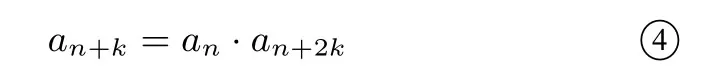
結(jié)論6在數(shù)列{an}中,若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有an+an+1+an+2+···+an+k-1=m(m∈R),則數(shù)列{an}是周期為k的周期數(shù)列.

證明由

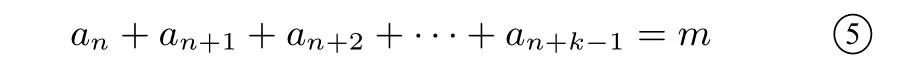
可得

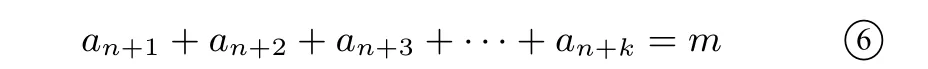
⑥式減⑤式得an+k-an=0,即an+k=an,所以數(shù)列{an}是周期為k的周期數(shù)列.

結(jié)論7在數(shù)列{an}(an/=0)中,若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有an·an+1·an+2·····an+k-1=m(m∈R,m/=0),則數(shù)列{an}是周期為k的周期數(shù)列.

證明由

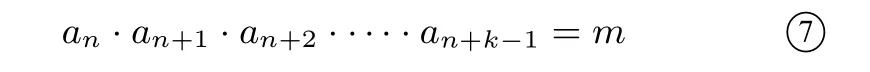
可得

⑧式除⑦式可得an+k=an,所以數(shù)列{an}是周期為k的周期數(shù)列.

結(jié)論8在數(shù)列{an}中,若存在正整數(shù)k,使得對(duì)于任意正整數(shù)n,都有an·an+1·an+2·····an+k-1=an+an+1+an+2+···+an+k-1,且an+1·an+2·····an+k-1/=1,則數(shù)列{an}是周期為k的周期數(shù)列.

證明由

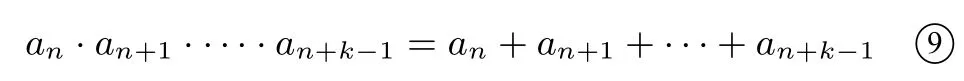
可得

⑩式減⑨式可得

(an+1·an+2·····an+k-1-1)(an+k-an)=0,

又因?yàn)閍n+1·an+2·····an+k-1/=1,所以an+k=an,即數(shù)列{an}是周期為k的周期數(shù)列.

應(yīng)用

例1(高一“希望杯”試題)數(shù)列{an}對(duì)于每個(gè)n≥3(n∈N+)都有an=an-1-an-2,若前2015項(xiàng)和為a(a/=0),則S5=()

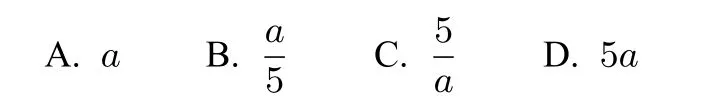
解析an=an-1-an-2(n≥3)變形可得an=an-1+an+1(n≥2).由結(jié)論4可知數(shù)列{an}是周期為6的周期數(shù)列,所以S5=S2015=a,故選A.

例2(北京高考題改編)設(shè)數(shù)列{an},a1=2且滿(mǎn)足對(duì)任意n∈N+,都有an+an+1=5,則a2018=___.

解析因?yàn)閍n+an+1=5,由結(jié)論6可知,數(shù)列{an}是周期為2的周期數(shù)列,所以a2018=a2=3.

例3(河南高中數(shù)學(xué)競(jìng)賽題改編)已知數(shù)列{an}中,a1=1,a2=2,且對(duì)n∈N+,有an·an+1·an+2=an+an+1+an+2(an+1·an+2/=1),則S2019=____.

解析由結(jié)論8可知,數(shù)列{an}是周期為3的周期數(shù)列,由a1=1,a2=2可得a3=3,所以S2019=673×(a1+a2+a3)=4038.