MACROSCOPIC REGULARITY FOR THE BOLTZMANN EQUATION?
Feimin HUANG(黃飛敏)Yong WANG(王勇)
School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China;Academy of Mathematics and System Sciences,CAS,Beijing 100190,China
E-mail:fhuang@amt.ac.cn;yongwang@amss.ac.cn
Abstract The regularity of solutions to the Boltzmann equation is a fundamental problem in the kinetic theory.In this paper,the case with angular cut-o ffis investigated.It is shown that the macroscopic parts of solutions to the Boltzmann equation,i.e.,the density,momentum and total energy are continuous functions of(x,t)in the region R3×(0,+∞).More precisely,these macroscopic quantities immediately become continuous in any positive time even though they are initially discontinuous and the discontinuities of solutions propagate only in the microscopic level.It should be noted that such kind of phenomenon can not happen for the compressible Navier-Stokes equations in which the initial discontinuities of the density never vanish in any finite time,see[22].This hints that the Boltzmann equation has better regularity e ff ect in the macroscopic level than compressible Navier-Stokes equations.
Key words Boltzmann equation;macroscopic regularity;compressible Navier-Stokes equations
1 Introduction
In this paper,we consider the Boltzmann equation
where F(t,x,v)is a distribution function for the gas particles at time t>0,position x∈R3and particle velocity v∈R3.The collision operator Q(F,F)takes the following bilinear form

where the relation between the post-collison velocity(v′,u′)of the two particles with precollision velocity pair(v,u)is given by
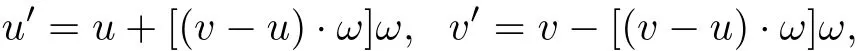
satisfying
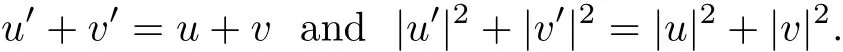
Throughout this paper,we consider the hard and soft potentials with angular cut-o ff,i.e.,
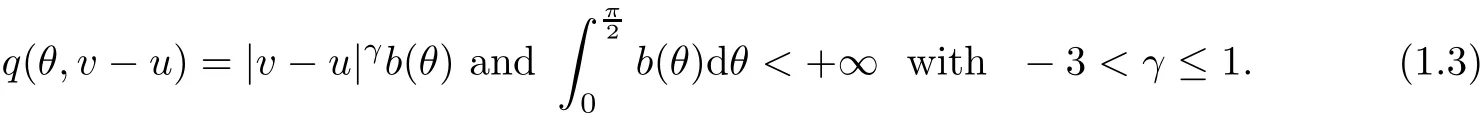
We impose the Boltzmann equation(1.1)with initial condition

There is an enormous literature on the study of well-posedness of the Cauchy problem for the Boltzmann equation.The existence of global renormalized solutions was first proved by DiPerna and Lions[13]for large initial data.However,little is known on the uniqueness of renormalized solution.For small initial data,various results on the existence and uniqueness of solutions were obtained,see[4,6,14,19–21,23–25,29,30]and references therein.We also refer to the monographs[5,11,17]and survey paper[31].
On the other hand,the regularity of solutions is a key problem of the Boltzmann equation.For the case with angular cut-o ff,it is believed that the initial singularities propagate in time since the Boltzmann equation is hyperbolic.This property was proved by Boudin-Desvillettes[8]with propagation of Sobolevsingularity in the case near vacuum,later by Duan-Li-Yang[16]in the case near global Maxwellian.We also refer to[3,7,26,28]for other interesting works.For the case without angular cut-o ff,the solution is believed more regular since the non-cuto ffcollision operator behaves like a fractional Laplacian.For interesting results on this topic,we refer to[1,2,9,10,12,27]and the references therein.
It is well known that the Boltzmann equation is closely related to the compressible Navier-Stokes equations through Chapman-Enskog expansion.It is conjectured that the Boltzmann equation has regularity in the macroscopic components.In fact,the famous averging lemma[18]shows thatfor any smooth compact support function ?(v).This indicates that the macroscopic components like density,momentum and total energy probably haveregularity.However more regularity is not known from the average lemma.The purpose of this paper is to investigate better regularity for the macroscopic quantities of solutions to Boltzmann equation(1.1)with angular cut-o ff.We find that the Boltzmann equation has better macroscopic regularity beyond the compressible Navier-Stokes equations.Precisely speaking,we shall prove that the macroscopic parts of solutions to the Boltzmann equation,i.e.the density,momentum and total energy are continuous functions of(x,t)in the region R3×(0,+∞).In other words,these macroscopic quantities immediately become continuous in any positive time even though they are initially discontinuous and the discontinuities of solutions propagate only in the microscopic level.It should be noted that such kind of phenomenon can not happen for the compressible Navier-Stokes equations in which the initial discontinuities of the density never vanish in any finite time,see[22].This means that the Boltzmann equa-tion has better regularity e ff ect in the macroscopic level beyond the compressible Navier-Stokes equations.
De fine a weight function

and let the global Maxwellianμbe

Let F0be the initial data satisfying,for any fixed(x,t)∈ R3×(0,+∞),kwF0kL∞x,v<+∞ and
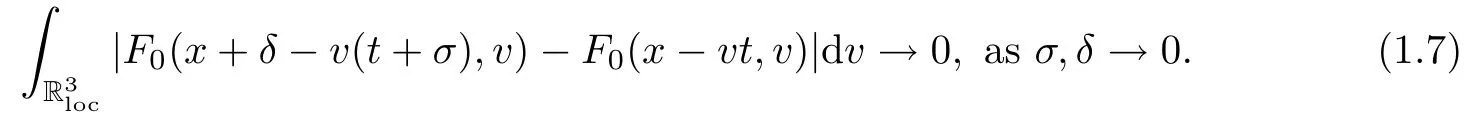
We note that the initial condition(1.7)is general.Indeed,there is a large class of initial data satisfying(1.7).For the case near global Maxwellian,we can choose,for example,that

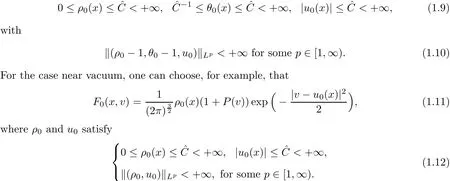
One can check that both(1.8)and(1.11)satisfy the condition(1.7),see Appendix A below.
The solutions considered in this paper are in the following space X:
Near Maxwellianμ,F(t,x,v)≥0 for a.e.(t,x,v)∈(0,+∞)×R3×R3and

Usually it is very hard to prove the existence of solutions in space X.However,we point out that the L∞mild solutions constructed in[15,20,30]near Maxwellian and[4,6,21,23,25]near vacuum do satisfy the conditions(1.13)and(1.14),respectively.For the sake of completeness,we shall write down the results[6,15]in Appendix B below.
Then our main results of this paper are as follows.
Theorem 1.1Let(1.3)hold,β >8+2max{0,γ},the initial data F0satis fies(1.7),and the solutions F(t,x,v)of Boltzmann equation belong to the space X,then the macroscopic components of solutions to the Boltzmann equation(1.1)are continuous functions of(x,t)in the region R3×(0,+∞).
Moreover,we have
Theorem 1.2Under the conditions of Theorem 1.1,and if the initial data F0further satis fies
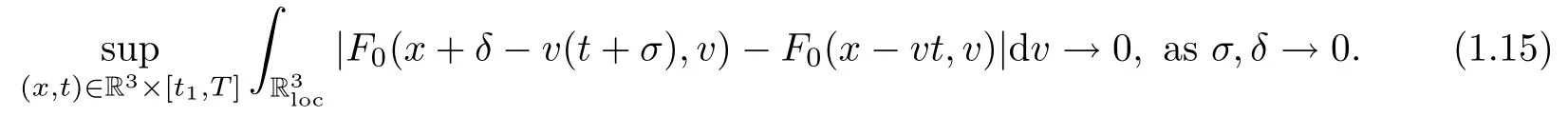
where t1and T are any given times with 0 A few remarks are in order. Remark 1.3It is noted that the condition(1.15)is slightly stronger than(1.7).Indeed,both examples in(1.8)and(1.11)satisfy(1.15)for any 0 Remark 1.4It is noted that even though the initial macroscopic parts in Theorems 1.1 and 1.2 are allowed to be discontinuous in x∈R3(the possible discontinuous set has zero measure),the macroscopic components of solutions to the Boltzmann equation immediately become continuous in(x,t)for any positive time t>0.Such kind of phenomenon can not happen for the compressible Navier-Stokes equations in which the initial discontinuities of the density never vanish in any finite time,see[22].This hints that the Boltzmann equation has better regularity e ff ect in the macroscopic level beyond the compressible Navier-Stokes equations,and the discontinuities of solutions to the Boltzmann equation propagate only in the microscopic level. Remark 1.5If β >8+2max{0,γ}+k,k ∈ R+,let B(v)be any function satisfying|B(v)|≤C(1+|v|)2+k,then,by the same arguments as in the proof of Theorems 1.1 and 1.2,one can still prove that has the same results as in Theorems 1.1 and 1.2. Remark 1.6As explained previously,the solutions constructed in[15,20,30]near Maxwellian and[4,6,21,23,25]near vacuum belong to X,see appendix B for details on the results of[6,15].If their initial data further satisfy(1.7)(or(1.15)),then Theorem 1.1(or Theorem 1.2)holds.That is,the macroscopic quantities of their solutions are continuous in(x,t).Thus,Theorems 1.1 and 1.2 are self-contained in this sense. The proof of Theorem 1.1 and Theorem 1.2 is based on the following observation.Since the Boltzmann equation is essentially transport,the solution propagates along the velocity v direction.Thus the integral with respect to v can be translated to the integral with respect to x by the change of variables.The continuity of macroscopic components is then derived from the continuity of translations onspace.The formula of collision operator plays important role in the whole proof. The rest of this paper is arranged as follows.Section 2 is devoted to the proof of Theorems 1.1,1.2. NotationsThroughout this paper,C denotes a generic positive constant which may depend on β,γ and vary from line to line.C(t)denotes the generic positive continuous function depending on time t>0 and β,γ which also may vary from line to line.k ·kL2denotes the standard Let F(t,x,v)be the solution of Boltzmann equation(1.1),we write down the Duhamel form of the solution to Boltzmann equation(1.1).For(t,x,v)∈(0,+∞)×R3×R3,one has that Proof of Theorem 1.1For any fixed.The continuity of density ρ(x,t)in(x,t)is equivalent to show that That is,for any ε>0,we need to prove that there exists χ >0,which may depend on(x,t)and ε,such that if|σ|≤ χ and|δ|≤ χ, We assume σ ≥ 0 without loss of generality and denotefor notation simplicity.We divide the proof into two parts.The proof is based on the initial condition(1.7)and the continuity of translations on Lp. Part 1Estimation on First,we note that it follows from(1.7)that It is straightforward to obtain,for β >3+max{0,γ},that where C1will be chosen later.Using(2.22)and the same arguments as in(2.17),for β>3+max{0,γ},we have where we have used the fact that and C1is chosen large so that(2.23)holds.Thus,from(2.19)–(2.23),there exists χ4>0 depending on t and ε such that if σ ≤ χ4,it holds that where we have used the fact that where p is de find in(2.15).Therefore,for β >6+2max{0,γ},combining(2.32)–(2.34),there exists χ5>0 depending on t and ε such that if σ +|δ|≤ χ5,it holds that It follows from(2.31)that For J21212,we follow the idea of[5].Denote Then it follows from(2.30)and(2.40)that Combining(2.36)–(2.38)and(2.43),for β >6+max{0,γ},there exists χ6>0 depending on t and ε such that if σ +|δ|≤ χ6,one has that It remains to estimate J22.A direct calculation shows that It follows from(2.29),for β >6+max{0,γ},that We only consider J2241since the argument for J2242is similar.It holds that By the same arguments as in(2.20)and(2.21),one can get that Combining(2.45)–(2.54),for β >6+2max{0,γ},there exists χ7>0 depending on t and ε such that if σ ≤ χ7,one has that Thus it follows from(2.27),(2.28),(2.35),(2.44)and(2.55),β >6+2max{0,γ},that Proof of Theorem 1.2For any fixed 0 By the same arguments as in(2.6),one has,for β>3,that It follows from(1.15)that there exists χ1>0 depending on,T and ε such that if σ+|δ|≤ χ1,one has that which,together with(2.60),for β>3,that On the other hand,by the same arguments as in(2.8)–(2.25),one can prove that there exists χ2>0 depending on,T and ε such that if σ +|δ|≤ χ2,it holds,for β >6+2max{0,γ},that As in(2.27)–(2.56),one can prove that there exists χ3>0 depending on,T and ε such that if σ +|δ|≤ χ3,one obtains,for β >6+2max{0,γ},that Appendix A We shall prove that the examples given in(1.8)and(1.11)satisfy the condition(1.7)and(1.15).Here we only give the proof for(1.8)since the case for(1.11)is similar. Using(1.9),it is obvious that kwF0kL∞≤C<∞.Next we prove the second part of(1.7).We only need to prove that for any small ε>0,there exists χ >0 depending on t,ε such that if σ +|δ|≤ χ,it holds that where we have used the continuity of translations on Lp.Thus there exists χ1>0 depending on t>0 and ε>0 such that if σ +|δ|≤ χ1,it holds that For L2,it is straightforward to obtain that where C2(t)is a large constant.Hence one obtains that Similarly,we can deal with the remaining terms of(A.5).Therefore,there exists χ2>0 depending on t and ε such that if σ ≤ χ2,it holds that Combining(A.4)and(A.8),there exists χ =min{χ1,χ2}depending on t and ε such that(A.1)holds if σ +|δ|≤ χ.Therefore the condition(1.7)holds for the example given in(1.8). Finally,for any fixed 0 Thus the example given in(1.8)also satis fies the condition(1.15). Appendix B Firstly,we introduce the existence results near Maxwellian.Indeed,Ukai-Yang[30]proved that the Cauchy problem for the Boltzmann equation(1.1)is well-posed globally in time for the cases 0≤γ≤1 near a global Maxwellian in function spaces L2∩L∞which do not need any regularity condition on the derivatives.Guo[20]gave another framework to solve the problem also without any regularity condition on the derivatives.Recently,the authors[15]obtained the global mild solution to the Boltzmann equation with large initial data for both hard and soft potentials,i.e.,?3<γ≤1.To introduce the result of[15],we denote It follows by a direct calculation that for all t≥0.Note,in particular,that E(F0)≥0 holds true for any function F0(x,v)≥0. Proposition B.1(see[15])Let?3< γ ≤ 1 and ? =T3or R3.For given β >max{3,3+suppose the initial data F0satis fiesThen there is a small constant ε0>0 depending onsuch that if the Boltzmann equation(1.1),(1.3),(1.4)has a global unique mild solution F(t,x,v)=μ(v)+satisfying(B.1)and wheredepends only on γ,β. Based on the L∞-estimate in(B.3),by the energy estimates,one can get easily,for β >,that where C depends only on the initial data.It is noted that the smallness condition on the initial data kf0kL2(?×R3)is not needed in(B.4).Here we point out that the condition?<γ≤1 in(B.4)is used to deal with the nonlinear term. Finally,we recall existence theorems to the Boltzmann equation(1.1)in the case near vacuum with small initial data.Here we use the result adapted to our study,which are inspired from[6]. Proposition B.2(see[6]) Let 0<γ≤1 and F0be an initial data such that where r>0 is a positive constant,k>0 is a suitably large constant and α>0 is a small positive constant depending on r,k.Then the Cauchy problem to the Boltzmann equation(1.1)has a unique global solution F(t,x,v),and satis fies the following estimate One can check directly that the above the solution in Proposition B.1 satis fies(1.13),while the solutions in Propositions B.2 satis fies(1.14).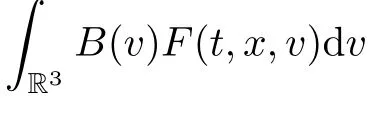
2 Proof of the Main Theorems


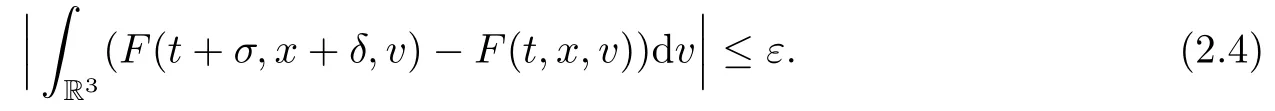




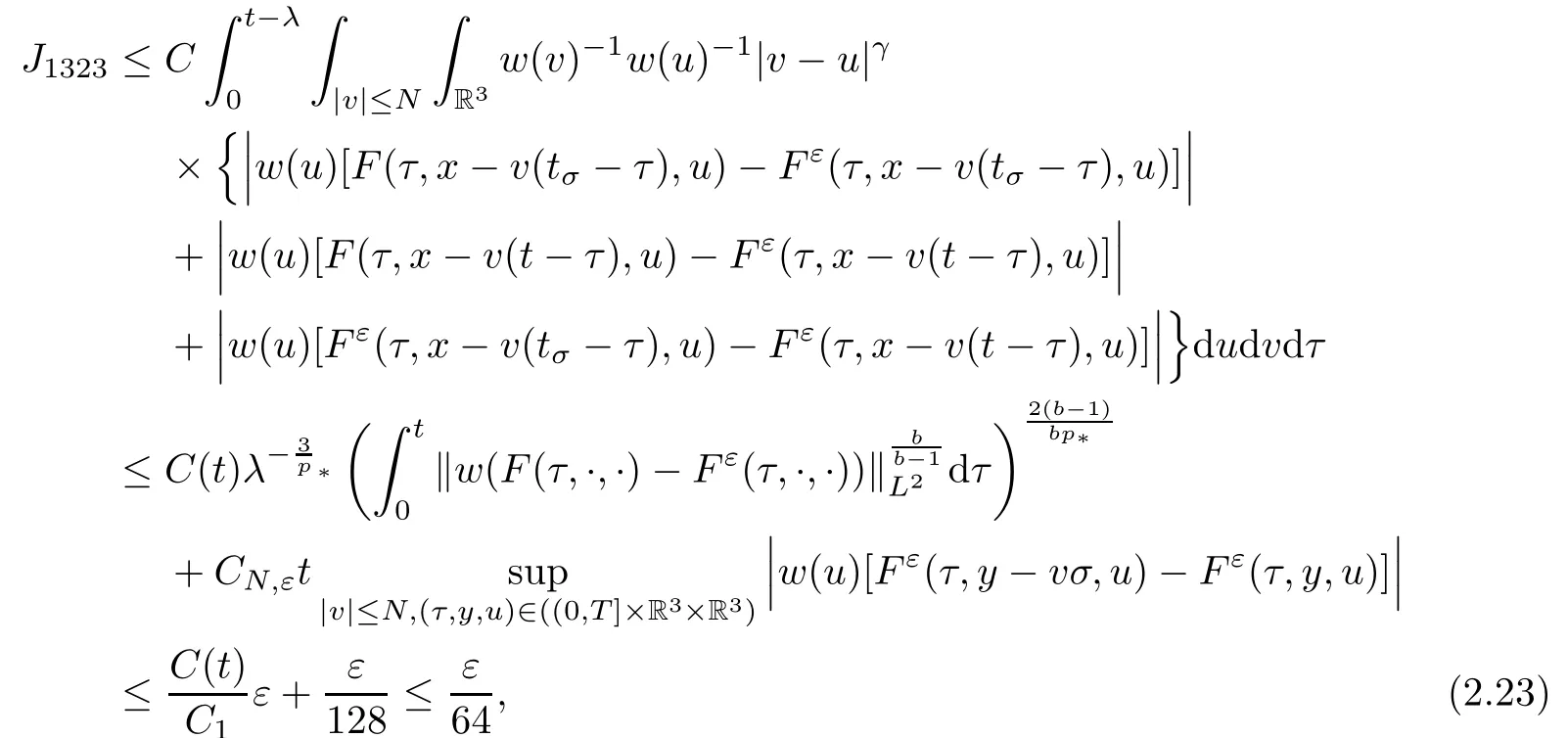
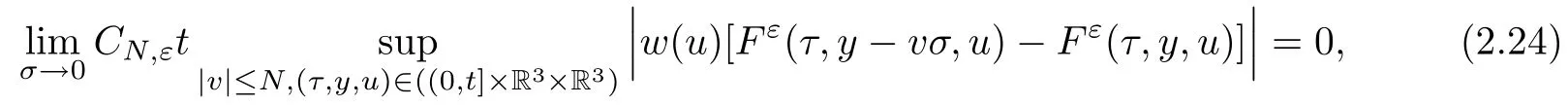
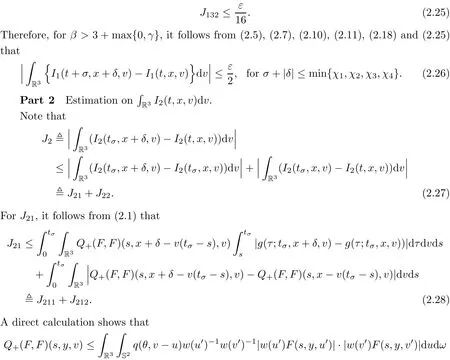

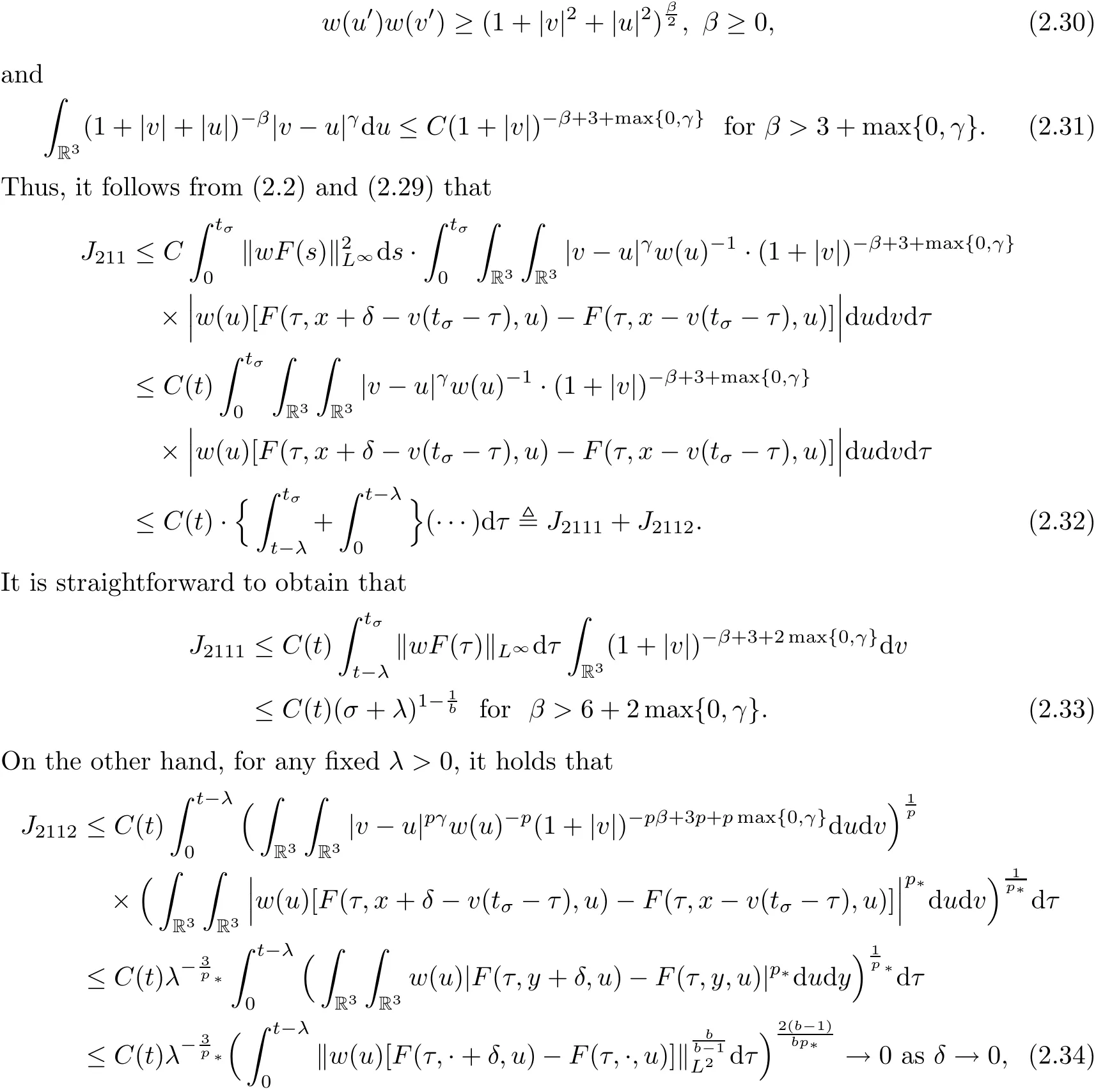




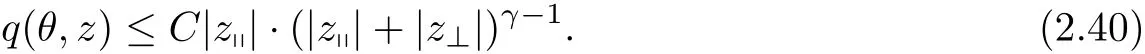

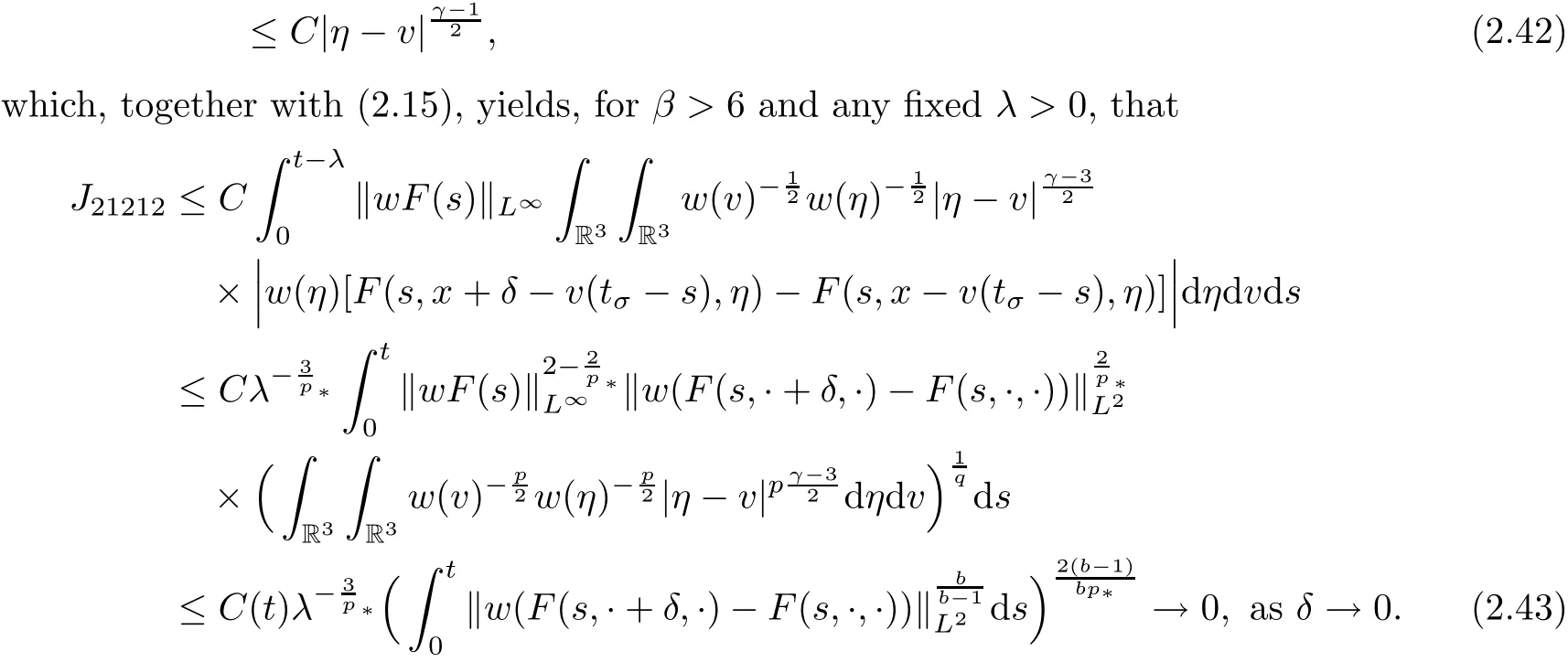
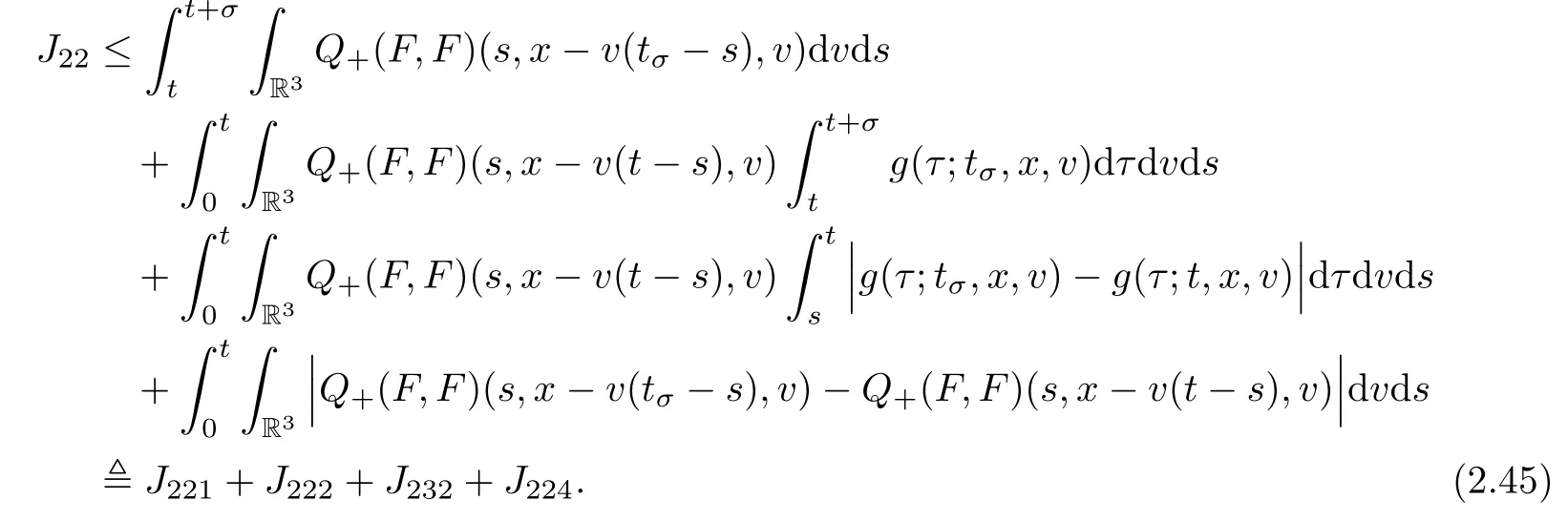


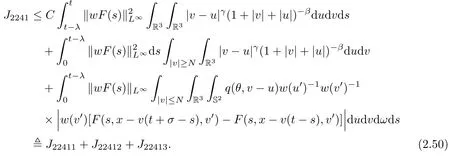



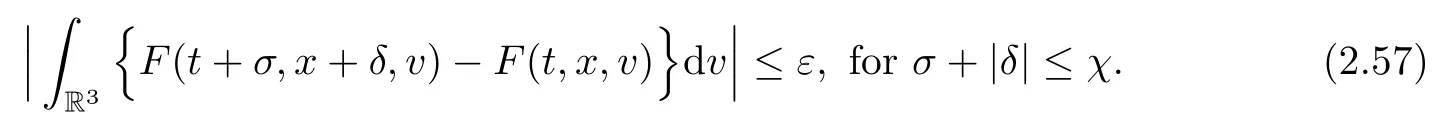





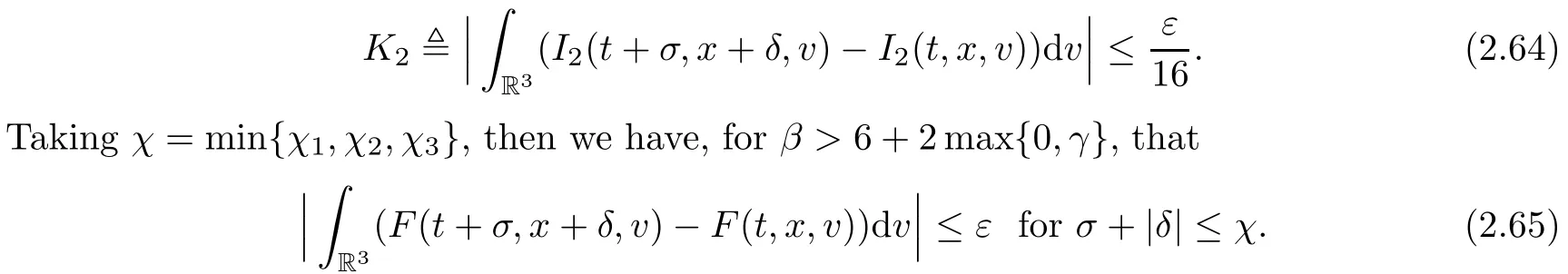




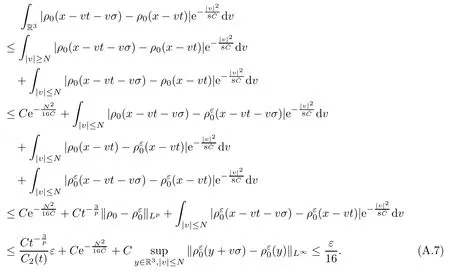


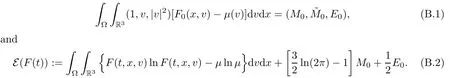
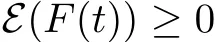


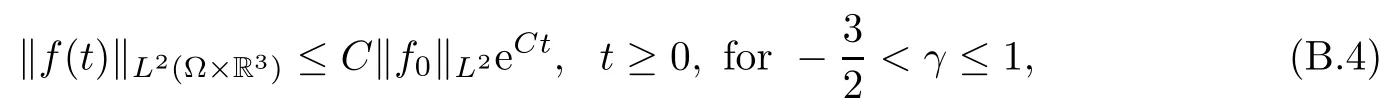


 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
