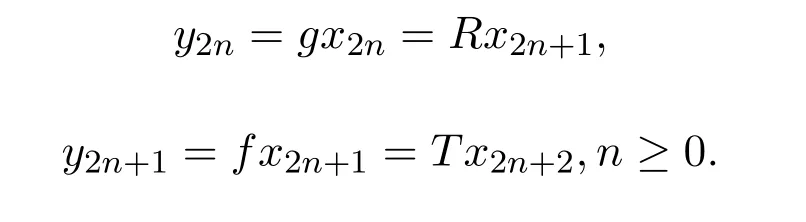S-度量空間中幾個(gè)映射的公共不動(dòng)點(diǎn)定理

黃琪,薛西鋒

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

非線性算子不動(dòng)點(diǎn)的存在性和唯一性問(wèn)題是非線性泛函分析中的的重要內(nèi)容,也是非線性泛函分析中的熱點(diǎn)研究問(wèn)題,因此關(guān)于不動(dòng)點(diǎn)的問(wèn)題在各類(lèi)度量空間都有研究.2012年,文獻(xiàn)[1]引入S-度量空間,研究了S-度量空間一些不動(dòng)點(diǎn)定理.2014年,文獻(xiàn)[2-4]討論了S-度量空間中的一些性質(zhì),在新的壓縮條件下利用其性質(zhì)得到并證明了S-度量空間中的一些不動(dòng)點(diǎn)定理.隨后,在文獻(xiàn)[5-12]中S-度量空間中的不動(dòng)點(diǎn)定理得到了很大的發(fā)展.受上述文獻(xiàn)的啟發(fā),本文在完備的S-度量空間中,引入一類(lèi)新的壓縮條件,然后在此壓縮條件下研究公共不動(dòng)點(diǎn)的存在性和唯一性問(wèn)題,所得的結(jié)果推廣了以前文獻(xiàn)中的相關(guān)結(jié)果.

2 預(yù)備知識(shí)

定義 2.1[5]設(shè)X是非空集,假設(shè)映射S:X3→[0,∞),?x,y,z,a∈X滿足:

(1)S(x,y,z)=0當(dāng)且僅當(dāng)x=y=z,

(2)S(x,y,z)≤S(x,x,a)+S(y,y,a)+S(z,z,a).

3 主要定理及結(jié)論

定理 3.1設(shè)f,g,R,T是完備的S-度量空間(X,S)的自映射,有f(x)?T(x),g(x)?R(x)且{f,R},{g,T},{R,T}是相容的,對(duì)任意的x,y,z∈X滿足條件:

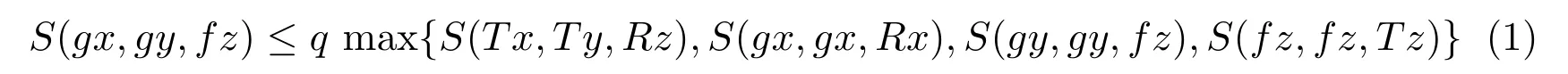
其中0

證明給定x0∈X,因g(x)?R(x),有x1∈X,使得gx0=Rx1,又當(dāng)fx1∈T(X),有x2∈X,使得fx0=Tx1,依次下去,有x2n+1∈X,使得gx2n=Rx2n+1且有x2n+2∈X,使得fx2n+1=Tx2n+2,有{xn}∈X,使得