有界半Hoops上的時態(tài)算子
牛海靈,辛小龍
(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710069)
1 引言
Hoops代數(shù)是自然序的交換剩余整幺半群,由文獻[1-2]引入.半Hoops是Hoops的一般化,它最初由文獻[3]引入,被稱為互補半群.半Hoops[4]是最基本的剩余結(jié)構(gòu),而且包含所有基于剩余格的邏輯代數(shù).它與剩余格[5]比較,半Hoops是交半格,不滿足并半格;與Hoops代數(shù)比較,半Hoops是不滿足可分性.
對于命題邏輯,經(jīng)典和非經(jīng)典邏輯都不包含時間維度,為了獲得時態(tài)邏輯,文獻[6]用新的一元算子來豐富給定的命題邏輯,用G,H,F,P表示,通常把這些算子叫做時態(tài)算子.時態(tài)算子F和P通過G和H來表示:
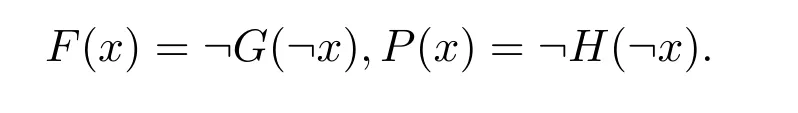
文獻[6]首次引入時態(tài)算子在經(jīng)典邏輯中,隨后,在非經(jīng)典邏輯中引入時態(tài)算子.比如說,Hetying代數(shù),Basic代數(shù)和Effect代數(shù)上的時態(tài)算子[7-9].近年來,越來越多的學(xué)者不斷地在不同邏輯代數(shù)中研究時態(tài)算子,如:模糊邏輯,MV-代數(shù)上,偽MV-代數(shù)上,不可交換剩余格上的時態(tài)算子[10-13]等.
基于以上內(nèi)容,拓展了時態(tài)算子在更廣泛的非經(jīng)典邏輯代數(shù)中,即半Hoops.給出了半Hoops上的時態(tài)算子及研究其性質(zhì),給出了時態(tài)濾子的定義,刻畫了時態(tài)濾子.探究了極大時態(tài)濾子,得到了一些重要結(jié)果.
2 預(yù)備知識
定義 2.1[4]一個(2,2,2,0)型的代數(shù)A=(A,⊙,→,∧,1)若滿足下列條件:
(1)(A,∧,1)是一個有最大元1的交半格;
(2)(A,⊙,1)是一個可換半群;
(3)(x⊙y)→z=x→(y→z),對任意的x,y,z∈A.
則稱 (A,⊙,→,∧,1)為半 Hoops代數(shù).
在一個半 Hoops代數(shù) (A,⊙,→,∧,1)上,定義對任意的x,y∈A,x≤y當(dāng)且僅當(dāng)x→y=1.易驗證≤是A上的偏序關(guān)系,對任意的x∈A,x≤1.
對任意的x∈A,定義x0=1且xn=xn?1⊙x對任意的n∈N.
命題 2.1[4]設(shè) (A,⊙,→,∧,1)是一個半 Hoops代數(shù).則下面性質(zhì)成立:對任意的x,y,z∈A,
(1)x⊙y≤z當(dāng)且僅當(dāng)x≤y→z;
(2)x⊙y≤x,y;
(3)1→x=x,x→1=1;
(4)xn≤x;
(5)y≤x→y;
(6)若x≤y,則y→z≤x→z,z→x≤z→y且x⊙z≤y⊙z;
(7)x→y≤(z→x)→(z→y),x→y≤(y→z)→(x→z);
(8)y⊙(y→x)≤x.
一個半Hoops(A,⊙,→,∧,1)稱為有界半Hoops,若存在一個元素0∈A使得對任意的x∈A有0≤x.
在一個有界半Hoops代數(shù)(A,⊙,→,∧,0,1)中,對任意的x∈A,通過?x=x→0定義運算“?”.若對任意的x∈A有??x=x,則稱這個有界半Hoops(A,⊙,→,∧,0,1)具有雙重否定性,簡稱為DNP條件.
為了方便,記有界半 Hoops代數(shù) (A,⊙,→,∧,0,1)為A.
命題2.2[14]設(shè)A是一個有界半Hoops代數(shù).則下面性質(zhì)成立:對任意的x,y∈A,
(1)?1=0,?0=1;(2)x≤??x;(3)?x=???x;
(4)若x≤y,則?y≤?x;(5)x→y≤?y→?x;
(6)?x→y≤?y→x.
命題 2.3[14]設(shè)A是一個有界半Hoops代數(shù).對任意的x,y∈A,定義

則以下條件等價:對任意的x,y,z∈A,
(1)∨在A是可交換的;
(2)若x≤y,則-x∨z≤y∨z;
(3)x∨(y∧z)≤(x∨y)∧(x∨z);
(4)∨是A上的并運算.
命題 2.4[14]一個半Hoops稱為是∨?半Hoops,若它滿足命題2.3中的其中一個條件.
命題 2.5設(shè)A是一個有界∨?半Hoops代數(shù).則下面性質(zhì)成立:對?x,y∈A,
(1)?(y∧z)≥?y∨?z;
(2)(x∧y)⊙z≤(x⊙z)∧(y⊙z).
3 有界半 Hoops上的時態(tài)算子
定義3.1設(shè)A是一個有界半Hoops代數(shù)且G,H:A→A是一元算子.(A,G,H)稱為時態(tài)半Hoops,(G,H)稱為時態(tài)算子,若滿足下列條件,對任意的x,y∈A,
(A1)G(1)=H(1)=1;
(A2)G(x→y)≤G(x)→G(y),H(x→y)≤H(x)→H(y);
(A3)x≤GP(x),x≤HF(x),其中P(x)=?H(?x),F(x)=?G(?x).
例 3.1設(shè)A={0,a,b,1}且0 則A是一個半Hoops[14].在A上定義算子G和H如下: 經(jīng)過驗證可知,G和H是A上的時態(tài)算子. 命題3.1設(shè)(A;G,H)是一個時態(tài)半Hoops,則下面性質(zhì)成立:對任意的x,y∈A, (1)F(0)=P(0)=0; (2)若x≤y,則O(x)≤O(y),其中O∈{G,H,F,P}; (3)G(x)⊙G(y)≤G(x⊙y),H(x)⊙H(y)≤H(x⊙y); (4)對于A的任意一族元素{xi}i∈I,有G(∧xi)≤ ∧G(xi)和H(∧xi)≤ ∧H(xi); (5)PG(x)≤??x,FH(x)≤??x,特別地,PG(?x)≤?x,FH(?x)≤?x; (6)G(x→y)≤F(x)→F(y),H(x→y)≤P(x)→P(y); (7) (8)P≤PGP,F≤FHF. 證明(1)由F(x)和P(x)的定義可知,(1)成立. (2)由(A2)可知,當(dāng)x≤y時,有G(x)≤G(y).若x≤y,則?y≤?x.由算子G的單調(diào)性可知,有G(?y)≤G(?x),進而?G(?x)≤?G(?y).因此F(x)≤F(y). 其余證明類似. (3)由A(2)可知,G(x→y)⊙G(x)≤G(y).令y=y⊙x,得到 算子H的證明類似. (4)對任意的j∈I,因為∧xi≤xj,則G(∧xi)≤G(xj),進而G(∧xi)≤ ∧G(xi). 算子H的證明類似. (5)由A(3),得出對任意的x∈A,x≤HF(x).所以?x≤HF(?x). 因為x≤??x,則?G(??x)≤?G(x).因此 特別地,因為?x=???x,所以PG(?x)≤ ?x. 其余證明類似. 另一個不等式證明類似. (8)由A(3)可知,x≤GP(x).又由(2),則P(x)≤PGP(x). 另一個不等式證明類似 命題 3.2設(shè)(A;G,H)是一個時態(tài)半Hoops且滿足DNP條件,則下面性質(zhì)成立:對任意的x,y∈A, (1)PG(x)≤x,FH(x)≤x; (2)P=PGP,F=FHF; (3)對于A的任意一族元素{xi},有G(∧xi)=∧G(xi)和H(∧xi)=∧H(xi). 證明(1)由命題3.1(5)和x=??x可知,(1)成立. (2)由命題3.1(8)和命題3.2(1)可知,(2)成立. (3)設(shè)對任意的i∈I,y≤G(xi).由命題3.1(2)可知,P(y)≤PG(xi)≤xi,所以P(y)≤∧xi,進而y≤GP(y)≤G(∧xi).另一方面,由3.1(4)可得.因此(3)成立. 一個框架是一個序?qū)?X,R),其中X是非空集合,R是X上的二元運算.集合X被認為是時間尺度,關(guān)系xRy表示 “x在y之前”和 “y在x之后”.假設(shè)A是一個半Hoops且X是一個集合.則AX是X到A的全部映射的集合,滿足運算: 驗證AX是半Hoops. 命題 3.3設(shè){xi|i∈I}和{yi|i∈I}是A的任意族元素.則 證明由命題2.5(2),對任意的i∈I, 因為對任意的i∈I,(xi→yi)⊙xi≤yi,所以 定理 3.1設(shè)A是一個∨-半Hoops且(X,R)是一個框.定義算子G?和H?是AX到自身的映射,其中對任意的f∈AX和x∈X, 則 (AX;G?;H?)是一個時態(tài)半Hoops. 證明(1)對任意的y∈X,f(y)=1,所以G?(f)=f.因此G?(1)=H?(1)=1. (2)對于f,g∈AX和x∈X,利用命題2.5(2)和命題3.3可得, 定義 4.1有界半HoopsA中的一個濾子F稱為時態(tài)濾子,若對任意的x∈F,則G(x),H(x)∈F. 例 4.1設(shè)A={0,a,b,c,d,1}且0 則A是一個半Hoops[14],其中對任意的x,y∈A,x∧y=x⊙(x→y).在A上定義算子G=H如下: 反復(fù)驗證可知G和H是A上的時態(tài)算子,且F={1,a}是時態(tài)濾子. 記全體濾子為Ft(A). 注 4.1設(shè)A是一個有界半Hoops且F是A的一個時態(tài)濾子.F是一個真濾子當(dāng)且僅當(dāng)0. 定義 4.2設(shè) (A;G,H)是時態(tài)半Hoops.定義A上的運算ρ如下:對任意的x∈A,ρ(x)=x⊙G(x)⊙H(x). 易驗證A中的濾子是時態(tài)濾子當(dāng)且僅當(dāng)它關(guān)于運算ρ封閉. 對任意的n≥1,定義ρ0(x)=x,ρn+1(x)=ρ(ρn(x)).同時,對A中的任意非空子集X,定義ρk(X)如下: 命題 4.1設(shè)(A;G,H)是時態(tài)半Hoops.則對任意的x,y∈A和n,k≥1,下列性質(zhì)成立: (1)ρn(0)=0,ρn(1)=1,ρn+1(x)≤ρn(x); (2)若x≤y,則ρn(x)≤ρn(y); (3)ρk(x)⊙ρk(y)≤ρk(x⊙y). 證明(1)和(2)是顯然的. (3)由命題3.1(3)可知, 設(shè)A是半Hoops且X是A的非空子集.則X生成的時態(tài)濾子是指包含X的最小時態(tài)濾子,記為. 推論 4.1設(shè)F是A的時態(tài)濾子且x∈A.則 證明證明類似于定理4.1. 定義4.3設(shè)A是半Hoops且M是A的真時態(tài)濾子.M稱為A的極大時態(tài)濾子,若它沒有真包含在A的任何其它真時態(tài)濾子中.記A中的所有時態(tài)濾子的集合為M(A). 命題 4.2設(shè)A是半Hoops且M是A的真時態(tài)濾子.則下列條件等價: (1)M∈M(A); (2)若,則 證明(1)?(2)若,則M?因為M∈M(A),所以 (2)?(1)設(shè)G是A的真時態(tài)濾子使得M?G且MG,則存在x∈G使得.由(2)可知,因為所以A=G,這與G?A中矛盾.因此M∈M(A). 命題 4.3設(shè)A是半Hoops且M是A的真時態(tài)濾子.則下列條件等價: (1)M是極大時態(tài)濾子; (2)對任意的x∈AM,存在f∈M和n∈N使得f⊙ρ(x)n=0. 證明(1)?(2)設(shè)M是A的極大時態(tài)濾子.若x∈AM.由命題4.2可知,由推論 4.1和 0∈A可得 0≥f⊙ρ(x)n.因此f⊙ρ(x)n=0. (2)?(1)設(shè)G是A的真時態(tài)濾子使得M?G.則存在x∈G使得.由 (2),存在f∈M和n∈N使得f⊙ρ(x)n=0,所以 0∈G,從而G=A.因此,M是極大時態(tài)濾子. 定理4.2設(shè)A是有界半Hoops且M是A的真時態(tài)濾子.若M是A的極大時態(tài)濾子.則對任意的當(dāng)且僅當(dāng)存在n∈N使得?ρ(x)n∈M. 證明(1)?(2)設(shè)M是極大時態(tài)濾子且x∈A.若,由命題4.3可得,存在f∈M和n∈N,使得f⊙ρ(x)n=0,所以f≤ρ(x)n→0=?ρ(x)n.因為M是濾子,所以?ρ(x)n∈M. (2)?(1)設(shè)x∈A且存在n∈N使得?ρ(x)n∈M.假設(shè)x∈M.因為M是時態(tài)濾子,則對任意的n∈N,使得ρ(x)n∈M,從而 0=?ρ(x)n⊙ρ(x)n∈M,這與M是真濾子矛盾.因此對任意的.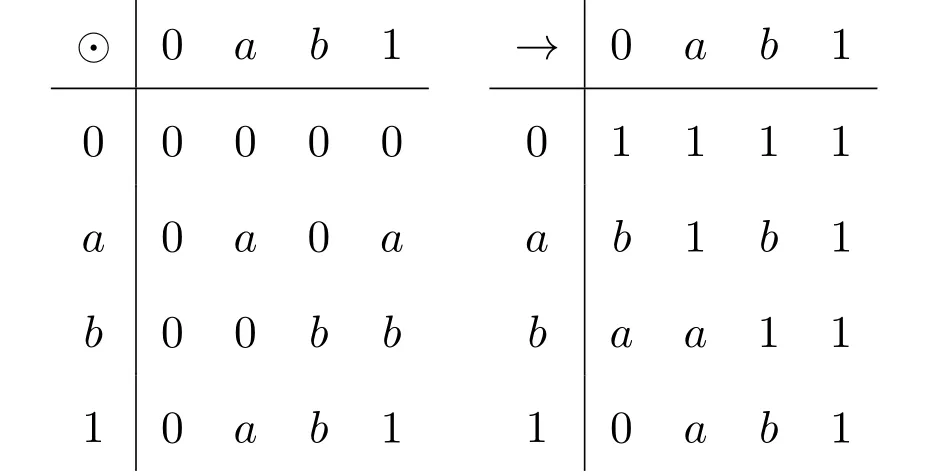



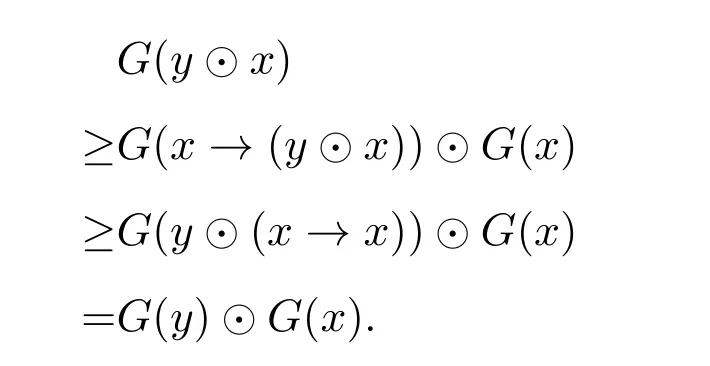
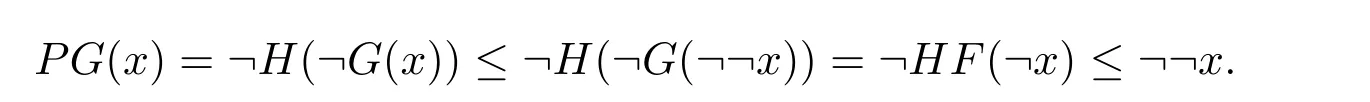

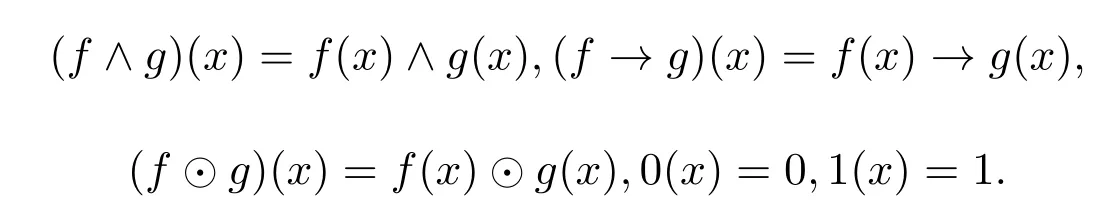


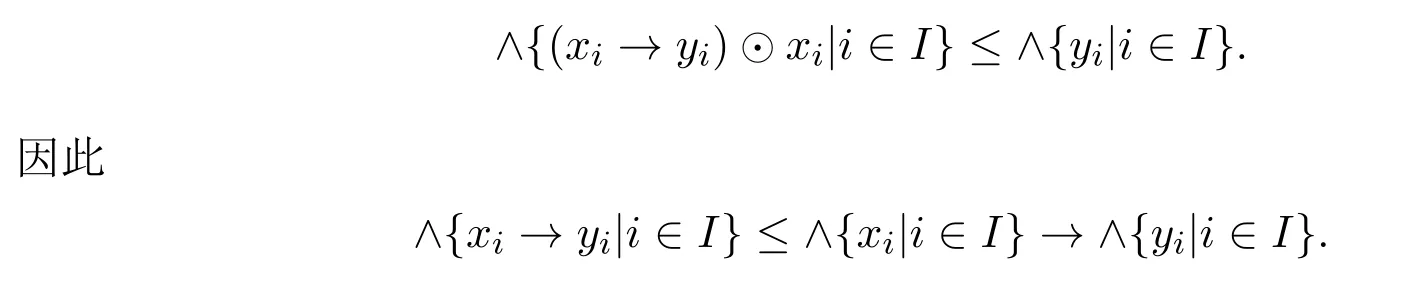


4 有界半 Hoops上的時態(tài)濾子