指對數(shù)不等式在導(dǎo)數(shù)壓軸題中的應(yīng)用
江西省宜豐中學(xué) (336300) 晏偉峰 賴仁定
在數(shù)學(xué)解題中我們常用到兩個不等式ex≥x+1和lnx≤x-1,而導(dǎo)數(shù)與以上兩個指對數(shù)不等式的證明問題是高考的熱點問題.本文結(jié)合實例,分析此類不等式的解題方法,以期拋磚引玉.
例1 (2019宜豐中學(xué)期末試題)已知函數(shù)f(x)=lnx-ax+1,g(x)=x(ex-x).(1)若直線y=2x與函數(shù)f(x)的圖像相切,求實數(shù)a的值;(2)若存在對任意x1∈(0,+∞),x2∈R,使f(x1)=g(x2)=0,且x1-x2>1,求實數(shù)a的取值范圍;(3)當(dāng)a=-1時,求證:f(x) 解析:(1)(2)略;(3)要證不等式f(x)≤g(x)+x恒成立等價于證明lnx+1 證法一:∵ex≥x+1?xex≥x(x+1)=x2+x,又lnx≤x-1即x≥lnx+1,∴x2+x≥x2+lnx+1.∴xex≥x2+lnx+1.由于對數(shù)不等式和指數(shù)不等式的等號不能同時成立,∴xex>x2+lnx+1. 證法二:∵lnx≤x-1?lnx+1≤x?lnx+1≤x·1≤x·(ex-x),∴xex≥x2+lnx+1.由于對數(shù)不等式和指數(shù)不等式的等號不能同時成立,∴xex>x2+lnx+1. 例2 (2019江西師大附中月考題)已知函數(shù)f(x)=ax+lnx+1.(1)若a=-1,求函數(shù)f(x)的最大值;(2)對任意x>0,不等式f(x)≤xex恒成立,求實數(shù)a的取值范圍. 例4 (2019年江淮十校聯(lián)考題)已知函數(shù)f(x)=x(e2x-a)-lnx,若f(x)≥1在(0,+∞)上恒成立,則實數(shù)a的取值范圍是( ). A.(-∞,e-1]B.(-∞,e-1) C.(-∞,2]D.(-∞,2) 解析:此題和例2本質(zhì)上是同一題,易得選C. 由上述實例可見,指對數(shù)不等式在此類導(dǎo)數(shù)壓軸題型求解中起到四兩撥千斤的作用,為學(xué)生的解題贏得了寶貴的時間.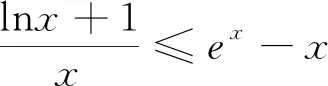
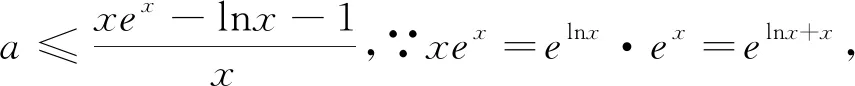
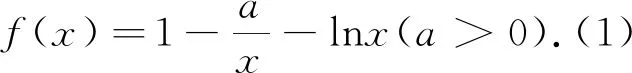
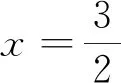
——來自一道幾何概型習(xí)題的錯解分析與思考

