The Isomorphic Classes of Small Degree Cayley Graphs over Dicyclic Groups
Cheng Tao Feng Lihua Liu Weijun Chen Quanguo Tang Lang
(1.School of Mathematics and Statistics, Shandong Normal University, Jinan, Shandong 250014, China;2.School of Mathematics and Statistics, HNP-LAMA, Central South University New Campus, Changsha, Hunan 410083, China;3.School of Mathematical Sciences, Qufu Normal University, Qufu, Shandong 273165, China;4.Mathematics and Computational Science, Hunan First Normal University, Changsha, Hunan 410205, China)
Abstract In this paper, we completely classify the isomorphic classes of the small degree(quartic, quintic and sextic)Cayley graphs over the dicyclic group T4p=
Key words Cayley graph Dicyclic group Spectrum Isomorphic class Quadratic reciprocity
1 Introduction

In this paper, we are interested in Cayley graphs-a special class of regular graphs.Given a finite groupGand a subsetS?G{1} withS=S-1, the Cayley graphX(G,S)has vertex setGand two verticesa,bare adjacent ifa-1b∈S.X(G,S)is connected ifSgeneratesG.
For a finite groupG, let Γ=Cay(G,S)for some subsetS?G{1}.Letσbe an automorphism ofG.Thenσnaturally acts on the vertex setV=G.LetT=Sσ.Then it is easily shown thatσinduces an isomorphism fromCay(G,S)to the Cayley graphCay(G,T), such an isomorphism is called a Cayley isomorphism.However, it is of course possible that two Cayley graphsCay(G,S)andCay(G,T)are isomorphic but there are no Cayley isomorphisms mappingStoT.This leads us to try to find the conditions under whichCay(G,S)?Cay(G,S)if and only ifSσ=Tfor someσ∈Aut(G).
A Cayley graphCay(G,S)is called a CI-graph ofGif, wheneverCay(G,S)?Cay(G,T), there is an elementσ∈Aut(G)such thatT=Sσ.(CI stands for Cayley Isomorphism).A finite groupGis called a CI-group if all Cayley graphs ofGare CI-graphs.
The problem of seeking CI-groups has received considerable amount of attention over the past fourty years, beginning with a conjecture ofdám[1]that all finite cyclic groups were CI-groups, one may refer to the surveys in[2,14,23,24].dám’s conjecture was disproved by Elspas and Turner[8].Since then, many mathematician are devoted to classifying cyclic CI-groups(see, for example, Djokovic[7], Babai[4], Alspach and Parsons[3], Palfy[22]and Godsil[10]), and finally, Muzychuk[20,21]obtained a complete classification of cyclic CI-groups.For other related results, one may refer to[19]and their references.
The investigation of CI-graphs is also closely related to the determination of the isomorphic classes of Cayley graphs.In view of the definition, ifX(G,S)is a CI-graph, then to judgeX(G,S)is isomorphic toX(G,T), we only need to decide whether or not there exists an automorphismσsuch thatσ(S)=T.Li[16]and[26]determined the isomorphic classes of some families of Cayley graphs which are edge-transitive but not arc-transitive.For more results about CI-graphs and the isomorphic classes of Cayley graphs, one may refer to[14]and the references therein.
Huang et al.[12]determined the isomorphic classes of cubic Cayley graphs on dihedral groups.Inspired by their results, we are interested in the dicyclic group of order 4p.For an odd primep, the dicyclic group of order 4pis presented asT4p=
2 Preliminaries
In this section, we introduce some notations and present several results which will be used later.
For a finite groupG, we denote byIRR(G)andIrr(G)the complete set of non-equivalent irreducible representations ofGand the complete set of non-equivalent irreducible characters ofG, respectively.We need the characters of cyclic groups.
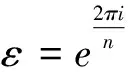
The following lemma is essential for our results, which involves spectral graph theory and representations and characters of finite groups.
Lemma 2.2([5]) LetGbe a finite group of ordern,S?G{1} be such thatS=S-1, andIrr(G)={χ1,…,χh} withχi(1)=di(i=1,…,h).Then the spectrum of the Cayley graphX(G,S)can be arranged as
Spec(X(G,S))={[λ11]d1,…,[λ1d1]d1,…,[λh1]dh,…,[λhdh]dh}.
Furthermore, for any natural numbert, we have
Our focus is on the dicyclic group.In general, the presentation for dicyclic groupT4nis given by
T4n=
Fornodd, settingx2=aandt=b, then we may rewriteT4nas
T4n=
This group has order 4n, and we have
T4n={ak,akb,akb2,akb3| 0≤k≤n-1}.
Lemma 2.3For the dicyclic groupT4n=
(1)akb=ba-k;akb2=b2ak;akb3=b3a-k;
(2)(akb)-1=akb3;(akb2)-1=a-kb2.
ProofBy relationsan=b4=1 andb-1ab=a-1, the results follow immediately.
Then+3 conjugacy classes ofT4nare listed as follows
{ajb| 0≤j≤n-1}, {ajb3| 0≤j≤n-1}.
Now we get the character table ofT4n.
Lemma 2.4([13]) Fornodd, the character table ofT4n=
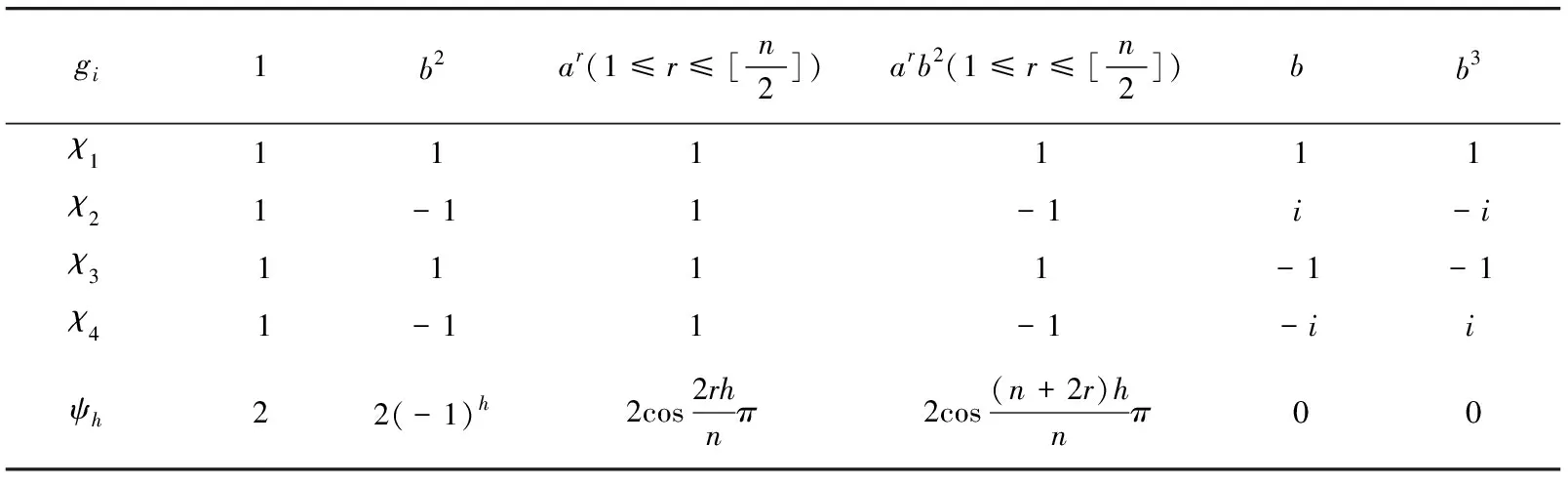
Table 1 The character table of T4n for n odd
By Lemmas 2.2 and 2.4, we have
Theorem 2.5([6]) LetT4nbe the dicyclic group andS?T4n{1} satisfyingS=S-1.Then we have
Spec(X(T4n,S))={[λg]1;[μh1]2,[μh2]2g=1,2,3,4;h=1,2,…,n-1},
and
(1)
We also need some notations for our convenience.For any characterχand two subsetsA,Bof a groupG, we denoteχ(A)=∑a∈Aχ(a)andχ(AB)=∑a∈A,b∈Bχ(ab).In particular,χ(A2)=∑a1,a2∈Aχ(a1a2).
For oddn, in the dicyclic groupT4n, we setS1?∪b2andS2?b∪b3.By Theorem 2.5, we obtain the following explicit formula for the spectrum ofX(T4n,S).
Corollary 2.6For oddn, letT4n=
Spec(X(T4n,S))={[λg]1;[μh1]2,[μh2]2|g=1,2,3,4;h=1,2,…,n-1},
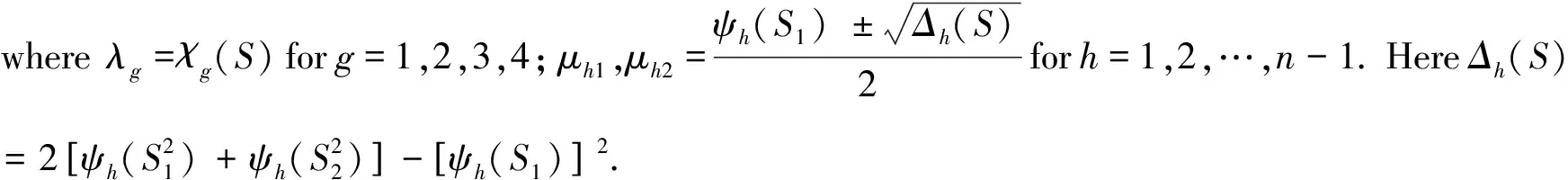
ProofNote thatS1S2={s1s2|s1∈S1,s2∈S2}?b∪b3andS2S1?b∪b3.By Lemma 2.4, we haveψh(S1S2)=0=ψh(S2S1).Thus
Then, the spectrum ofX(T4n,S)presented in(1)satisfies
(2)
From(2), we have thatμh1andμh2are the roots of the following quadratic equation
(3)
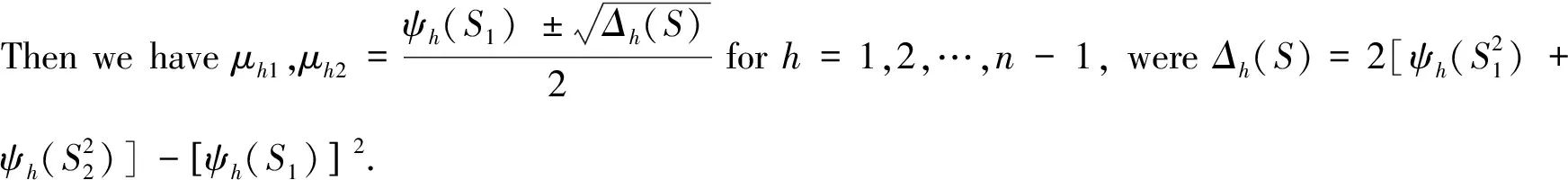
Lemma 2.7([15]) For oddn, letT4n=
By Lemma 2.7, we may obtain the automorphism group of the dicyclic groupT4n.
Theorem 2.8Suppose thatn>2 is odd andT4n=

whereσα,β(ak)=akα,σα,β(akb2)=akαb2,σα,β(aib)=aiα+βb,σα,β(aib3)=aiα+βb3, andτγ,δ(ak)=akγ,τa,δ(akb2)=akγb2,τγ,δ(aib)=aiγ+δb3,τγ,δ(aib3)=aiγ+δb.
ProofThe automorphism of cyclic groupaisσ(a)=ai, wheregcd(i,n)=1.And by Lemma 7, sinceZ(T4n)={1,b2}, for each automorphismσofT4n, we haveσ(b)=aβborσ(b)=atab3, whereβ∈n.Thus we define
σα,β(ak)=akα,σα,β(akb2)=akαb2,σα,β(aib)=aiα+βb,σα,β(aib3)=aiα+βb3,
and
τγ,δ(ak)=akγ,τγ,δ(akb2)=akγb2,τγ,δ(aib)=aiγ+δb3,τγ,δ(aib3)=aiγ+δb.
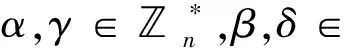
For a Cayley graphX(G,S)over a groupGwith respect toS, ifσ∈G, thenσinduces an isomorphism ΦσfromX(G,S)toX(G,σ(S)).Such an isomorphism is the so-called Cayley isomorphism.Thus we obtain

For an odd primep, Li et al.[15]showed that the dicyclic group is a CI-group.
Lemma 2.10([15]) For any odd primep, the dicyclic group
T4p=
of order 4pis a CI-group.
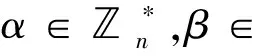
Then, from Lemmas 2.9 and 2.10, we deduce the following corollary.
Corollary 2.11LetX(T4p,S)andX(T4p,T)be two Cayley graphs onT4p.ThenX(T4p,S)?X(T4p,T)if and only ifS~T.
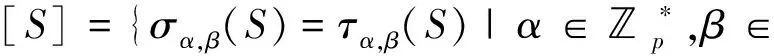
In the subsequent sections, we will discuss the isomorphic classes of Cayley graphsX(T4p,S), where |S|=4, |S|=5, and |S|=6.
3 Isomorphic Classes of quartic Cayley Graphs on T4p
Now we focus on the quartic Cayley graphX(T4n,S)with |S|=4.SinceX(T4n,S)is quartic andS=S-1, we can suppose thatS={ak,a-k,aib,aib3}, orS={akb2,a-kb2,aib,aib3}, orS={aib,aib3,ajb,ajb3}, wherek∈n{0},i,j∈nandi≠j.
Lemma 3.1For oddn, letX(T4n,S)be the quartic Cayley graph onT4nwith respect to S, whereS={ak,a-k,aib,aib3},S={akb2,a-kb2,aib,aib3}, orS={aib,aib3,ajb,ajb3}.ThenX(T4n,S)is connected.
ProofIfS={ak,a-k,aib,aib3}, thenakak=a2k.Sincenis odd, we havegcd(2k,n)=1, thena2kcan generatea, thusS=T4n, i.e.,X(T4n,S)is connected.
The remaining two cases can be obtained in the similar way, we omit the proof here.
By Corollary 2.6, we get the spectrum of the quartic Cayley graphX(T4n,S).
Lemma 3.2LetX(T4n,S)be the quartic Cayley graph onT4nwith respect toS.
(1)IfS={ak,a-k,aib,aib3}, then
whereΔh(S)=16 ifhis even, andΔh(S)=0 ifhis odd.
(2)IfS={akb2,a-kb2,aib,aib3}, then

(3)IfS={aib,aib3,ajb,ajb3}, then
ProofWe prove the result item by item.
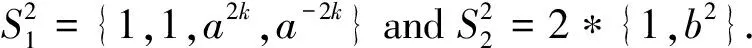
and
Therefore, we have

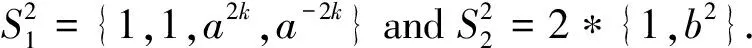
ψh(S1)=ψh(akb2)+ψh(a-kb2)
and
Therefore, we obtain
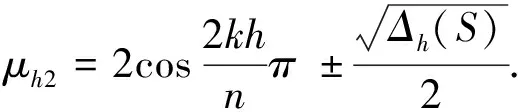
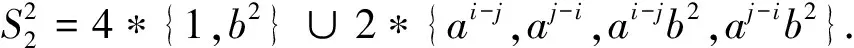
=8(ψh(1)+ψh(b2))+4(ψh(ai-j)+ψh(aj-i)+ψh(ai-jb2)+ψh(aj-ib2))

We complete this proof.
LetT4p=
Theorem 3.3For an odd primep, letX(T4p,S)be the quartic Cayley graph onT4pwith respect toS.Then, the following statements hold.
(1)IfS={ak,a-k,aib,aib3}, thenS~{a,a-1,b,b3}, i.e.,X(T4p,S)?X(T4p,{a,a-1,ab,ab3}).
(2)IfS={akb2,a-kb2,aib,aib3}, thenS~{ab2,a-1b2,b,b3}, i.e.,X(T4p,S)?X(T4p,{ab2,a-1b2,b,b3}).
(3)IfS={aib,aib3,ajb,ajb3}, thenS~{b,b3,ab,ab3}, i.e.,X(T4p,S)?X(T4p,{b,b3,ab,ab3}).
ProofWe do case by case.
(1)Sincepis a prime andk∈p{0},i∈p, we haveandi-k∈p.Takingandβ=i-k∈p, one can verify thatσα,β({a,a-1,b,b3})=S.This implies thatS~{a,a-1,b,b3}, and soX(T4p,S)?X(T4p,{a,a-1,ab,ab3})by Lemma 2.9.
(2)The proof is similar to that of(1).
(3)Sincepis a prime andi,j∈p,i≠j, we haveandβ=i∈p, one can easy verify thatσα,β({b,b3,ab,ab3})=S.This implies thatS~{b,b3,ab,ab3}, and soX(T4p,S)?X(T4p,{b,b3,ab,ab3})by Lemma 2.9.
Thus our result holds.
According to Theorem 3.3, we have
Corollary 3.4Letpbe an odd prime.Then the quartic Cayley graphs onT4phas only three isomorphic classes.
4 Isomorphic Classes of quintic Cayley Graphs on T4p
In this section, we focus on the quintic Cayley graphX(T4n,S)with |S|=5.SinceX(T4n,S)is quintic andS=S-1, there are only three types of this setS, i.e.,S={b2,ak,a-k,aib,aib3}, orS={b2,akb2,a-kb2,aib,xib3}, orS={b2,aib,aib3,ajb,ajb3}, wherek∈n{0},i,j∈nandi≠j.Comparing the setSin Section 3, here the setShas an additional elementb2.Thus, in the similar lines of Section 3, we get
Lemma 4.1For oddn, letX(T4n,S)be the quintic Cayley graph onT4nwith respect to S, whereS={b2,ak,a-k,aib,aib3}, {b2,akb2,a-kb2,aib,aib3}, or {b2,aib,aib3,ajb,ajb3}, andk∈n{0},i,j∈nandi≠j.ThenX(T4n,S)is connected.
Lemma 4.2LetX(T4n,S)be the quintic Cayley graph onT4nwith respect toS.
(1)IfS={b2,ak,a-k,aib,aib3}, then
|1≤h≤n-1},
whereΔh(S)=16 ifhis even, andΔh(S)=0 ifhis odd.
(2)IfS={b2,akb2,a-kb2,aib,aib3}, then
|1≤h≤n-1},

(3)IfS={b2,aib,aib3,ajb,ajb3}, then
Theorem 4.3For an odd primep, letX(T4p,S)be the quintic Cayley graph onT4pwith respect toS.Then, the following statements hold.
(1)IfS={b2,ak,a-k,aib,aib3}, thenS~{b2,a,a-1,b,b3}, i.e.,X(T4p,S)?X(T4p,{b2,a,a-1,ab,ab3}).
(2)IfS={b2,akb2,a-kb2,aib,aib3}, thenS~{b2,ab2,a-1b2,b,b3}, i.e.,X(T4p,S)?X(T4p,{b2,ab2,a-1b2,b,b3}).
(3)IfS={b2,aib,aib3,ajb,ajb3}, thenS~{b2,b,b3,ab,ab3}, i.e.,X(T4p,S)?X(T4p,{b2,b,b3,ab,ab3}).
Corollary 4.4Letpbe an odd prime.Then the quintic Cayley graphs onT4phas only three isomorphic classes.
5 Isomorphic Classes of sextic Cayley Graphs on T4p
In this section, we focus on the sextic Cayley graphX(T4n,S)with |S|=6.SinceX(T4n,S)is sextic andS=S-1, and for the graph to be connected, we can suppose that
· Type-I:S={ak1,a-k1,ak2,a-k2,aib,aib3},k1≠±k2,k1,k2∈n{0},i∈n;
· Type-II:S={ak1b2,a-k1b2,ak2b2,a-k2b2,aib,aib3},k1≠±k2,k1,k2∈n{0},i∈n;
· Type-III:S={ak1,a-k1,ak2b2,a-k2b2,aib,aib3},k1,k2∈n{0},i∈n;
· Type-IV:S={ak,a-k,ai1b,ai1b3,ai2b,ai2b3},k∈n{0},i1≠i2,i1,i2∈n;
· Type-V:S={akb2,a-kb2,ai1b,ai1b3,ai2b,ai2b3},k∈n{0},i1≠i2,i1,i2∈n;
· Type-VI:S={ai1b,ai1b3,ai2b,ai2b3,ai3b,ai3b3},i1≠i2≠i3,i1,i2,i3∈n.
Similar to Lemma 3.1, we have that the sextic Cayley graphX(T4n,S)is always connected.
Lemma 5.1For odd numbern, letX(T4n,S)be the sextic Cayley graph onT4nwith respect toS, whereSis one of the above types.ThenX(T4n,S)is connected.
From Lemma 2.4 and Corollary 2.6, we deduce the spectrum of the sextic Cayley graphX(T4n,S).
Lemma 5.2LetX(T4n,S)be the sextic Cayley graph onT4nwith respect toS.
(1)IfX(T4n,S)is of type-I, i.e.,S={ak1,a-k1,ak2,a-k2,aib,aib3}, then
|1≤h≤n-1},
whereΔh(S)=16 ifhis even, andΔh(S)=0 ifhis odd;
(2)IfX(T4n,S)is of type-II, i.e.,S={ak1b2,a-k1b2,ak2b2,a-k2b2,aib,aib3}, then
whereΔh(S)=16 ifhis even, andΔh(S)=0 ifhis odd;
(3)IfX(T4n,S)is of type-III, i.e.,S={ak1,a-k1,ak2b2,a-k2b2,aib,aib3}, then
|1≤h≤n-1},
whereΔh(S)=16 ifhis even, andΔh(S)=0 ifhis odd;
(4)IfX(T4n,S)is of type-IV, i.e.,S={ak,a-k,ai1b,ai1b3,ai2b,ai2b3}, then
|1≤h≤n-1},
(5)IfX(T4n,S)is of type-V, i.e.,S={akb2,a-kb2,ai1b,ai1b3,ai2b,ai2b3}, then
|1≤h≤n-1},
(6)IfX(T4n,S)is of type-VI, i.e.,S={ai1b,ai1b3,ai2b,ai2b3,ai3b,ai3b3}, then
ProofBy Corollary 6, the proof is similar to the proof of Lemma 3.2.
RemarkLetT4p=
Theorem 5.3For an odd primep, letX(T4p,S)be the sextic Cayley graph onT4pwith respect toS.We have that
(1)IfX(T4n,S)is of type-I, i.e.,S={ak1,a-k1,ak2,a-k2,aib,aib3}, thenS~{a,a-1,ak,a-k,b,b3}, i.e.,X(T4p,S)?X(T4p,{a,a-1,ak,a-k,b,b3}), wherek∈p{0,1,-1};
(2)IfX(T4n,S)is of type-II, i.e.,S={ak1b2,a-k1b2,ak2b2,a-k2b2,aib,aib3}, thenS~{ab2,a-1b2,akb2,a-kb2,b,b3}, i.e.,X(T4p,S)?X(T4p,{ab2,a-1b2,akb2,a-kb2,b,b3}), wherek∈p{0,1,-1};
(3)IfX(T4n,S)is of type-III, i.e.,S={ak1,a-k1,ak2b2,a-k2b2,aib,aib3}, thenS~{a,a-1,akb2,a-kb2,b,b3}, i.e.,X(T4p,S)?X(T4p,{a,a-1,akb2,a-kb2,b,b3}), wherek∈p{0};
(4)IfX(T4n,S)is of type-IV, i.e.,S={ak,a-k,ai1b,ai1b3,ai2b,ai2b3}, thenS~{a,a-1,b,b3,aib,aib3}, i.e.,X(T4p,S)?X(T4p,{a,a-1,b,b3,aib,aib3}), wherei∈p{0};
(5)IfX(T4n,S)is of type-V, i.e.,S={akb2,a-kb2,ai1b,ai1b3,ai2b,ai2b3}, thenS~{ab2,a-1b2,b,b3,aib,aib3}, i.e.,X(T4p,S)?X(T4p,{ab2,a-1b2,b,b3,aib,aib3}), wherei∈p{0};
(6)IfX(T4n,S)is of type-VI, i.e.,S={ai1b,ai1b3,ai2b,ai2b3,ai3b,ai3b3}, thenS~{b,b3,ab,ab3,aib,aib3}, i.e.,X(T4p,S)?X(T4p,{b,b3,ab,ab3,aib,aib3}), wherei∈p{0,1}.
ProofWe do case by case.
(1)Sincepis a prime andk1,k2∈p{0},k1≠±k2andi∈p, we havep{0,1}.Takingp, one can easy verify thatσα,β(S)={a,a-1,ak,a-k,b,b3}, wherep{0,1,-1}.This implies thatS~{a,a-1,ak,a-k,b,b3}, and soX(T4p,S)?X(T4p,{a,a-1,ak,a-k,b,b3})by Lemma 2.9.
(2)Similar to(1).
(3)Sincepis a prime andk1,k2∈p{0} andi∈p, we havep{0}.Takingp, one can easy verify thatgmaα,β(S)={a,a-1,ak,a-k,b,b3}, wherep{0}.This implies thatS~{a,a-1,akb2,a-kb2,b,b3}, and soX(T4p,S)?X(T4p,{a,a-1,akb2,a-kb2,b,b3})by Lemma 2.9.
(4)Sincepis a prime andi1,i2∈p,i1≠i2, we haveandβ=-i1k-1∈p, one can easy verify thatσα,β(S)={a,a-1,b,b3,aib,aib3, wherei=(i2-i1)k-1∈p{0}.This implies thatS~{a,a-1,b,b3,aib,aib3}, and soX(T4p,S)?X(T4p,{a,a-1,b,b3,aib,aib3})by Lemma 2.9.
(5)Similar to(4).
(6)Sincepis a prime andi1,i2∈p,i1≠i2, we haveandβ=-i1(i2-i1)-1∈p, one can easy verify thatσα,β(S)={b,b3,ab,ab3,aib,aib3}, wherei=(i3-i1)(i2-i1)-1∈p{0,1}.This implies thatS~{a,a-1,b,b3,aib,aib3}, and soX(T4p,S)?X(T4p,{a,a-1,b,b3,aib,aib3})by Lemma 2.9.
We complete the proof.
LetSbe the set consists of all subsets ofSofT4p, whereShas six elements and 1?S,S=S-1.The following result determines all equivalence classes ofS.
Lemma 5.4The following statements hold.
(1)Fork,l∈p{0,1,-1}, in type-I, letS={a,a-1,ak,a-k,b,b3} andT={a,a-1,al,a-l,b,b3}.Then[S]=[T]if and only ifk=lork=-lorkl=1 orkl=-1;
(2)Fork,l∈p{0,1,-1}, in type-II, letS={ab2,a-1b2,akb2,a-kb2,b,b3} andT={ab2,a-1b2,alb2,a-lb2,b,b3}.Then[S]=[T]if and only ifk=lork=-lorkl=1 orkl=-1;
(3)Fork,l∈p{0}, in type-III, letS={a,a-1,akb2,a-kb2,b,b3} andT={a,a-1,alb2,a-lb2,b,b3}.Then[S]=[T]if and only ifk=lork=-l;
(4)Fori,j∈p{0}, in type-IV, letS={a,a-1,b,b3,aib,aib3} andT={a,a-1,b,b3,ajb,ajb3}.Then[S]=[T]if and only ifi=jori=-j;
(5)Fori,j∈p{0}, in type-V, letS={ab2,a-1b2,b,b3,aib,aib3} andT={ab2,a-1b2,b,b3,ajb,ajb3}.Then[S]=[T]if and only ifi=jori=-j;
(6)Fori,j∈p{0,1}, in type-VI, letS={b,b3,ab,ab3,aib,aib3} andT={b,b3,ab,ab3,ajb,ajb3}.Then[S]=[T]if and only ifi=jori=-jorij=1 ori-ij-1=0 orj-ij-1=0 ori+j-ij=0.
ProofWe do case by case.


(2)Similar to(1).


(5)Similar to(4).

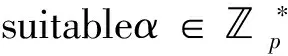
So we get the desired result.
In the remaining of this section, we will enumerate the isomorphic classes of sextic Cayley graphs onT4p.We only need to enumerate the isomorphic classes of those graphs of each type.For this purpose, the condition in Lemma 4 are called isomorphism conditions of sextic Cayley graphs onT4pof each type.From Lemma 4, we see that type-I and type-II have the same conditions, and type-III, type-IV and type-V have the same conditions.Thus, in the following discussion, we will divide into three cases.
1.Enumerating the isomorphic classes of sextic Cayley graphs onT4pof type-I(or type-II).
Fork,l∈p{0,1,-1}, we say thatkandlare equivalent, denoted byk?lifkandlsatisfy one of the isomorphism conditions, or equivalently,l∈{k,-k,k-1,-k-1}.It is easy to see that “?” defines an equivalence relation onp{0,1,-1}.Let[s]denote the equivalence class ofp{0,1,-1}.According to Theorem 3.3, we have
[k]={k,-k,k-1,-k-1}.
(4)
Moreover, from Lemma 5.4 we see that the number of equivalence classes ofp{0,1,-1}, denoted byN1, is just the number of isomorphic classes of sextic Cayley graphs onT4pof type-I.
Letpbe an odd prime.The Legendre symbol is a function ofpand an integeradefined as
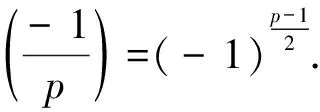
From Eq.(4)we know that[k]={k,-k,k-1,-k-1}, in which some elements may be equal.Forx,y∈[k], we list all the possibilities forx=yin Table 2.

Table 2 All the possibilities for x=y.
To determine the exact value ofN1, we need the following lemma.
Lemma 5.6Letp≥5 be a prime.We have
(1)ifp≡3(mod 4), then |[k]|=4, for allk∈p{0,1,-1};
(2)ifp≡1(mod 4), then the equationk2=-1 has exactly two distinct rootsk0,-k0, wherek0∈p{0,1,-1}.Furthermore,[k0]={k0,-k0} and |k|=4 for allk?{0,1,-1,k0,-k0}.
Proof
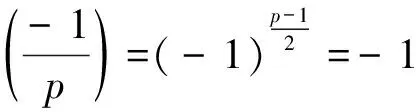
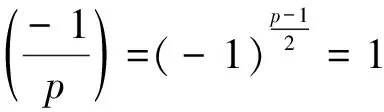
We complete the proof.
Note that ifp=3, then3{0,1,-1}=?, thusn1=0.By Lemma 5.3(1),(2), Lemma 5.4(1),(2)and Lemma 5.6, we get the following result immediately.
Theorem 5.7Letpbe an odd prime.Then the number of isomorphic classes of sextic Cayley graphs onT4pof type-I(or type-II)is given by
2.Enumerating the isomorphic classes of sextic Cayley graphs onT4pof type-III(or type-IV, or type-V).
Similar to the discussion in Case 1, fork∈p{0}, we can get the equivalence class ofp{0} is[k]={k,-k}.Thus the number of equivalence classes ofp{0}, denoted byN2, is just the number of isomorphic classes of sextic Cayley graphs onT4pof type-III.Sincek≠-k, we have |[k]|=2 for allk∈p{0}.Moreover, we get the following result immediately.
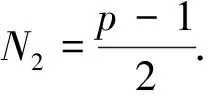
3.Enumerating the isomorphic classes of sextic Cayley graphs onT4pof type-VI.
Similar to the discussion in Case 1, fork∈p{0,1}, we can get the equivalence class ofp{0,1} is
[i]={i,i-1,1-i,(i-1)i-1,(1-i)-1,i(i-1)-1}.
Thus the number of equivalence classes ofp{0,1}, denoted byN3, is just the number of isomorphic classes of sextic Cayley graphs onT4pof type-VI.
To determine the exact value ofN3, we need the following lemma in[12].
Lemma 5.9[12] Letp≥5 be a prime.We have
(1)[2]={2,2-1,-1};
(2)ifp≡5(mod 6), then |[i]|=6, for alli?[2];
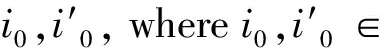
Note that ifp=3, then3{0,1}={2}=[2], thusN3=1.By Lemma 5.3(6), Lemma 5.4(6)and Lemma 5.9, we get the following result.
Theorem 5.10Letpbe an odd prime.Then the number of isomorphic classes of sextic Cayley graphs onT4pof type-VI is given by
By Theorems 5.8, 5.9 and 5.10, we obtain the main result of this section immediately.
Theorem 5.11Letpbe an odd prime.Then the number of isomorphic classes of sextic Cayley graphs onT4pis given by
ProofBy the aforementioned arguments, we haveN=2N1+3N2+N3.
Ifp=3, we haveN1=0,N2=1 andN3=1, thusN=2N1+3N2+N3=2·0+3·1+1=4.
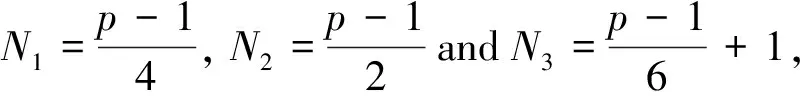

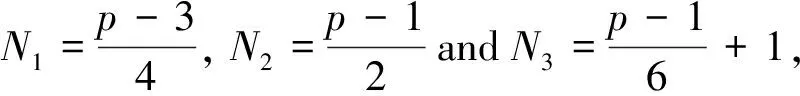
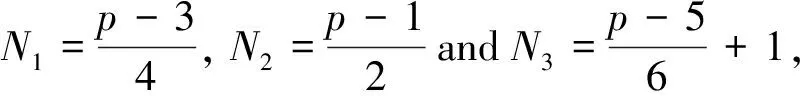
We complete the proof.
Now we give an example to show how to use the above method in Table 3.
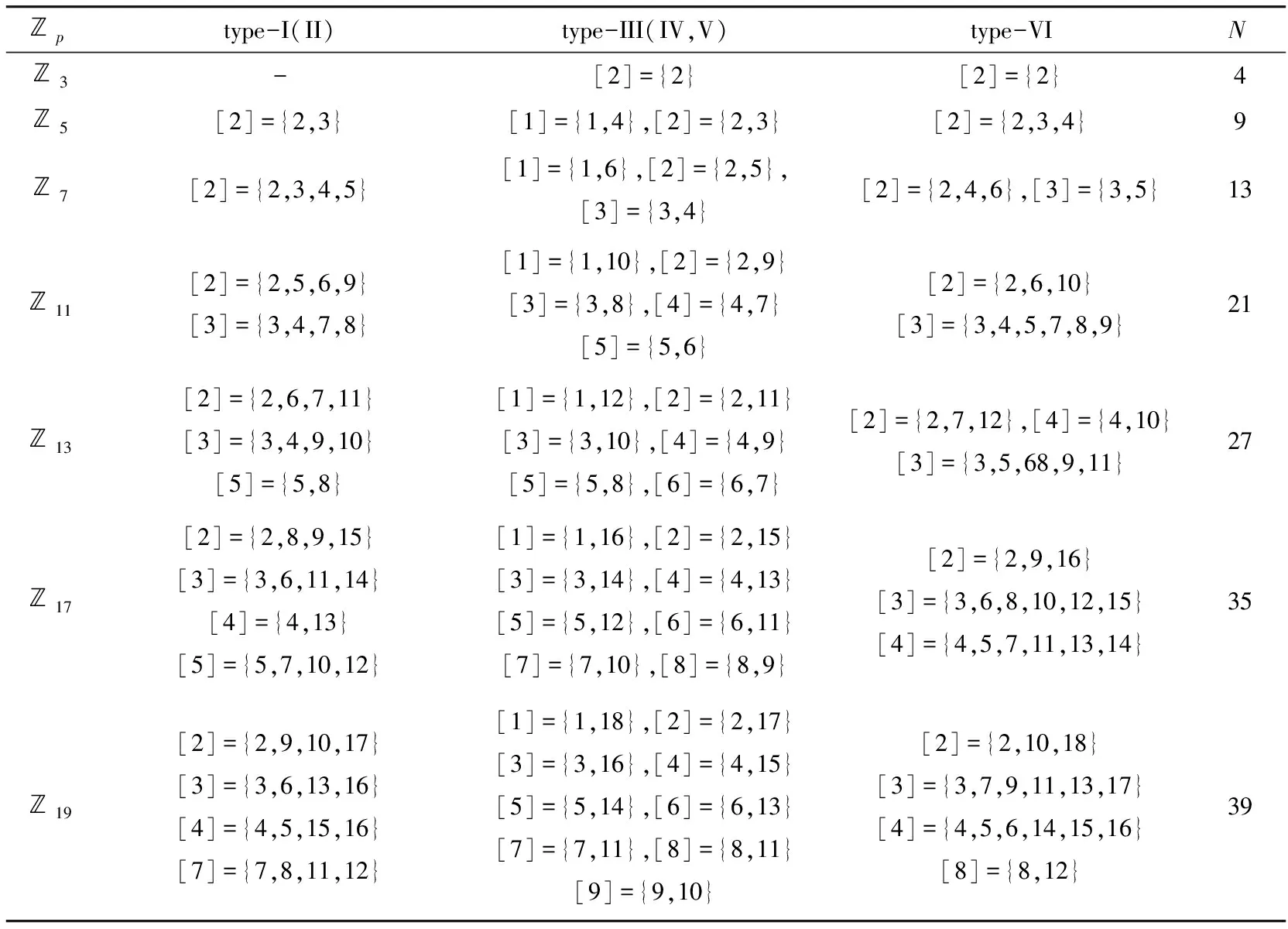
Table 3 The number of isomorphic classes for p≤19
 數(shù)學(xué)理論與應(yīng)用2020年4期
數(shù)學(xué)理論與應(yīng)用2020年4期
- 數(shù)學(xué)理論與應(yīng)用的其它文章
- 基于排隊(duì)論的機(jī)場(chǎng)上客區(qū)系統(tǒng)效益優(yōu)化研究
- The Twin Domination Number of Cartesian Product of Directed Cycle and Path
- An Isolated Toughness Condition for All Fractional(g,f,n,m)-Critical Deleted Graphs
- Two Generalized Successive Overrelaxation Methods for Solving Absolute Value Equations
- 非正規(guī)子群彼此同構(gòu)的有限群
- 兩類具有2-等變性的Liénard系統(tǒng)的全局動(dòng)力學(xué)
