The Twin Domination Number of Cartesian Product of Directed Cycle and Path
Ma Hongxia
(College of Preparatory, Xinjiang Normal University, Urumqi, Xinjiang 830017, China)
Abstract Let γ*(D)denote the twin domination number of digraph D and let Cm□Pn denote the Cartesian product of the directed cycle Cm and the directed path Pn, for m,n≥2. In this paper, we give a lower bound for γ*(Cm□Pn). Furthermore, we determine the exact values: γ*(C2□Pn)=n; γ*(C3□Pn)=n+2; γ*(C4□ γ*(C5□Pn)=2n+2.
Key words Twin domination number Cartesian product Directed cycle Directed path
1 Introduction
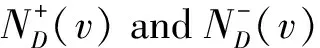
LetD1=(V1,A1)andD2=(V2,A2)be two digraphs which have disjoint vertex setsV1={x1,x2,…,xn1} andV2={y1,y2,…,yn2} and disjoint arc setsA1andA2, respectively.The Cartesian productD=D1□D2has vertex setV=V1×V2and(xi,yj)(xi′,yj′)∈A(D)if and only if one of the following holds:
(a)xi=xi′andyjyj′∈A2;
(b)yj=yj′andxixi′∈A1.
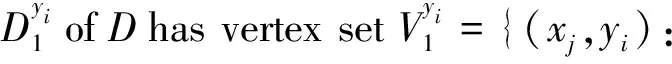
In this paper, we study the twin domination number ofCm□Pnand obtain the lower bound ofγ*(Cm□Pn).Furthermore, we determine the exact values ofγ*(Cm□Pn), whenm=2,3,4,5.
2 Main results
We emphasize that the vertices of a directed cycleCmare always denoted by the integers {0,1,…,m-1} and the vertices of a directed pathsPnare denoted by the integers {0,1,…,n-1}.These notations turned out to be convenient to formulate the proof of the following results.
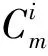
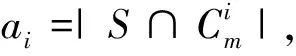
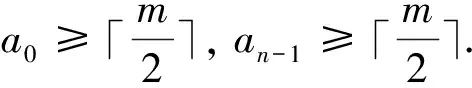

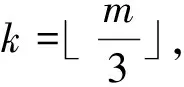
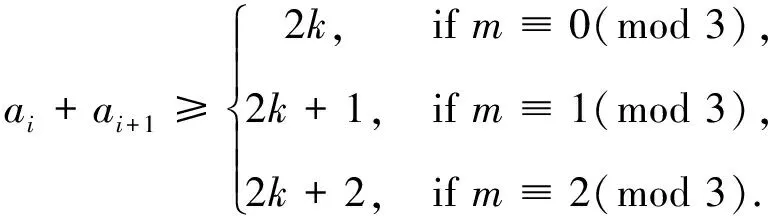
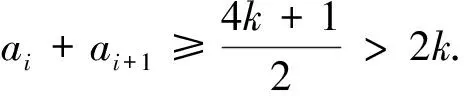
Letm=3k+1 andai≤k, thenai+ai+1≥2k+1.Whenai≥k+1, it is obvious thatai+ai+1≥2k+1 holds.Hence, whenm≡1(mod 3),ai+ai+1≥2k+1.
Letm=3k+2 andai≤k, thenai+ai+1≥2k+2.Whenai≥k+1, it is easy to see thatai+ai+1≥2k+2.Thus, we haveai+ai+1≥2k+2 form≡2(mod 3).
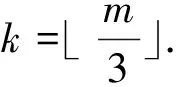

ProofLetSbe a twin dominating set ofCm□Pnwithn≥4.We apply the following algorithm:I=?,J=?,i=1;
Whilei≤n-3 do
ifai≥k+1 then
I=I∪{i};i=i+1
else
J=J∪{i,i+1};i=i+2
end if
end while.
From the above algorithm, we see that wheni=n-1 ori=n-2, the algorithm will stop.Hence we get two disjoint setsI,Jsuch that either {0,1,…,n-1}={0}∪I∪J∪{n-1} or {0,1,…,n-1}={0}∪I∪J∪{n-2,n-1}.
Therefore, we have
(1)
or
(2)
We consider the following three cases.
Case 1m≡0(mod 3).
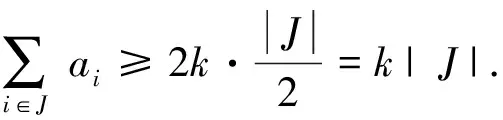
Subcase 1.11∈I.
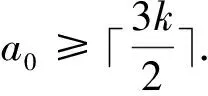
In the second case we get
Subcase 1.21?I.
Thusa1≤k.So we obtain thata0≥2kby Lemma 2.1.Then by(1)
According to(2), we get that
|S|≥2k+|I|(k+1)+(n-3-|I|)k+3k
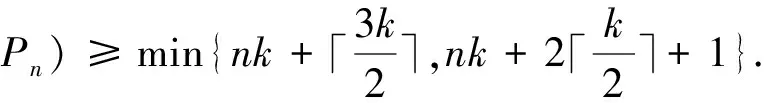
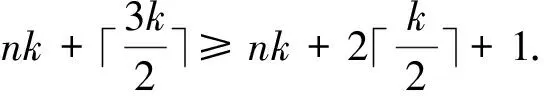
Case 2m≡1(mod 3).
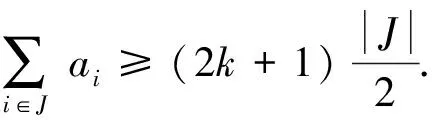
Similarly, if 1∈I, then
Otherwise
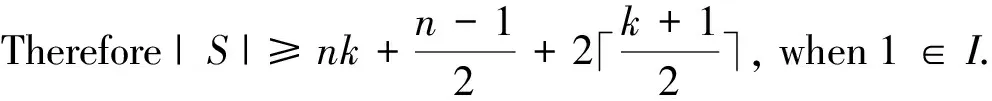
If 1?I, we can obtain thata0≥2k+1 by Lemma 2.1.Thus,
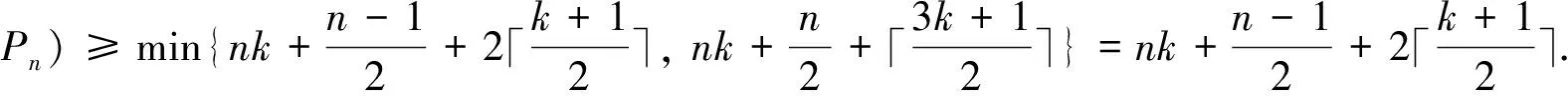
Case 3m≡2(mod 3).
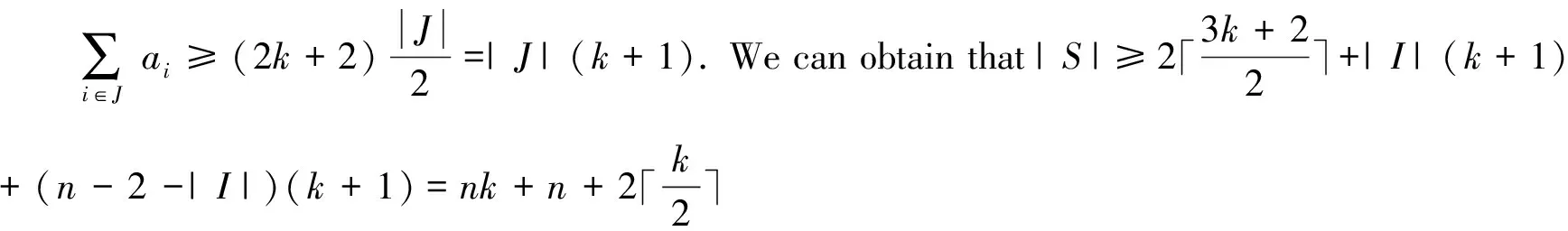
We now investigate the twin domination number ofC2□Pn.
It is clear thatγ*(C2□P2)=2 andγ*(C2□P3)=3.Whenn≥4, by Theorem 2.3, we haveγ*(C2□Pn)≥n.We define a setS1={(0,j)|j∈{0,1,…,n-1}}.It is easy to see thatS1is a twin dominating set ofC2□Pnand |S1|=n.Therefore we obtain the following Theorem.
Theorem 2.4Letn≥2, thenγ*(C2□Pn)=n.
We now consider the twin domination number of Cartesian productC3□Pnand define a setS2(see Figure 1)as:S2={(0,0),(2,0);(0,j)j≡0(mod 3);(1,j)j≡1(mod 3);(2,j)j≡2(mod 3), forj≥1}.Note that |S2|=n+1.
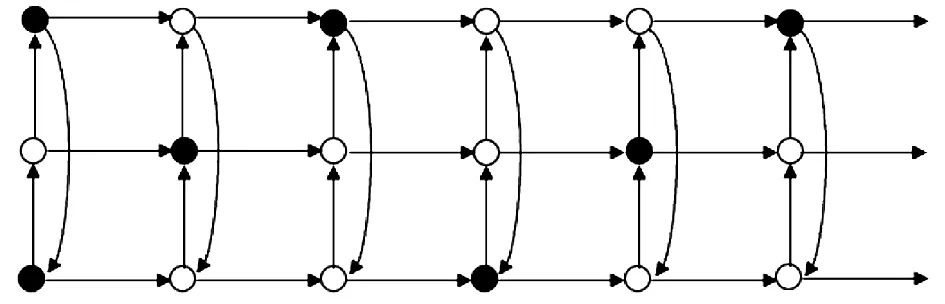
Figure 1 The set S2
Theorem 2.5Letn≥2, thenγ*(C3□Pn)=n+2.
ProofIt is easy to calculate thatγ*(C3□P2)=4 andγ*(C3□P3)=5.Letn≥4, by Theorem 2.3, we getγ*(C3□Pn)≥n+2.
Note thatS2∪{(0,n-1)} is a twin dominating set ofC3□Pn, whenn≡0,2(mod 3).Similarly,S2∪{(2,n-1)} is a twin dominating set ofC3□Pn, whenn≡1(mod 3).Thusγ*(C3□Pn)=n+2.
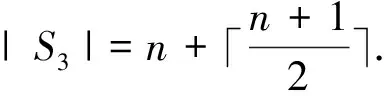
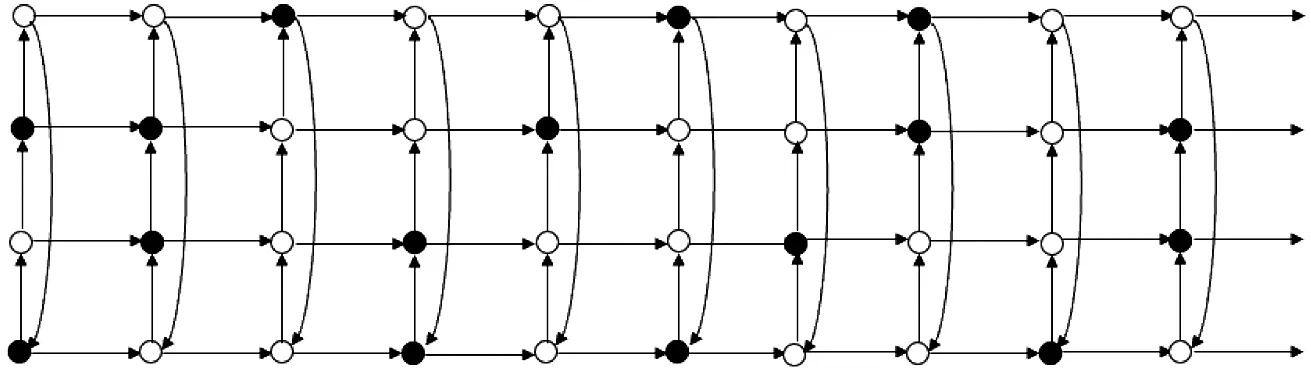
Figure 2 The set S3
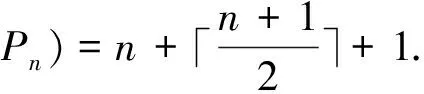
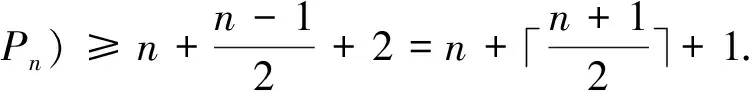
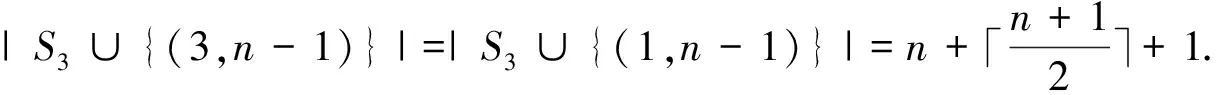
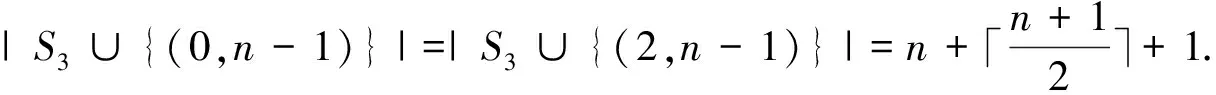
We consider the twin domination number of Cartesian productC5□Pn, and define a setS4(see Figure 3)as:S4={(0,0),(2,0),(4,0),(0,j),(2,j)j≡0(mod 3);(1,j),(3,j)j≡1(mod 3);(2,j),(4,j)j≡2(mod 3), forj≥1}.Note that |S4|=2n+1.
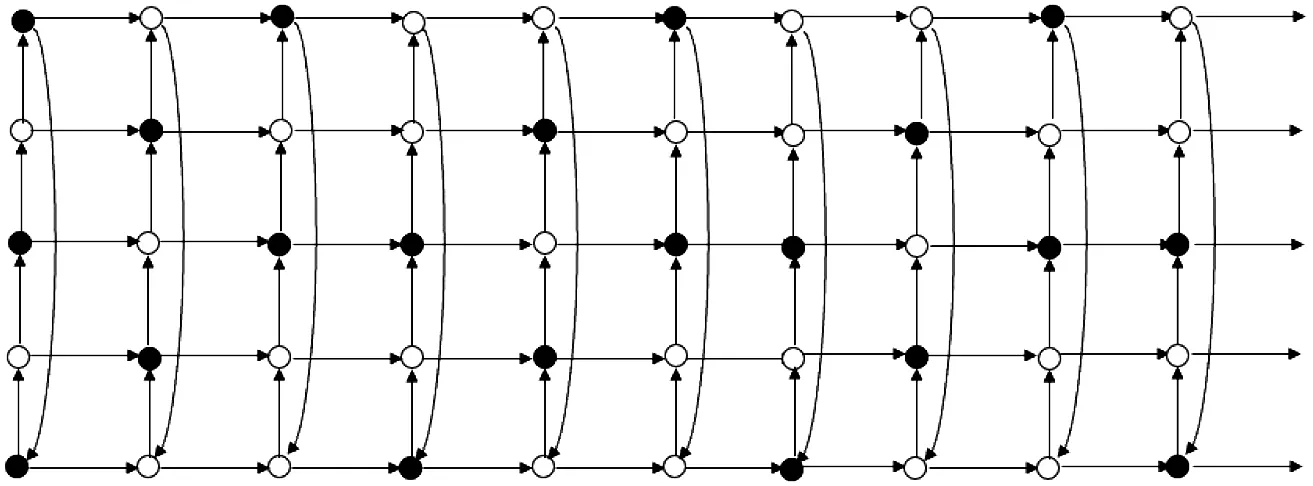
Figure 3 The set S4
It is easy to see thatγ*(C5□P2)=6 andγ*(C5□P3)=8.Whenn≥4, we obtain thatγ*(C5□Pn)≥2n+2 by Theorem 2.3.
Note thatS4∪{(4,n-1)} is a twin dominating set ofC5□Pn, whenn≡1,2(mod 3).Similarly,S4∪{(0,n-1)} is a twin dominating set ofC5□Pn, whenn≡0(mod 3).Therefore we can obtain the following Theorem.
Theorem 2.7Letn≥2, thenγ*(C5□Pn)=2n+2.
 數(shù)學(xué)理論與應(yīng)用2020年4期
數(shù)學(xué)理論與應(yīng)用2020年4期
- 數(shù)學(xué)理論與應(yīng)用的其它文章
- 基于排隊(duì)論的機(jī)場(chǎng)上客區(qū)系統(tǒng)效益優(yōu)化研究
- An Isolated Toughness Condition for All Fractional(g,f,n,m)-Critical Deleted Graphs
- Two Generalized Successive Overrelaxation Methods for Solving Absolute Value Equations
- The Isomorphic Classes of Small Degree Cayley Graphs over Dicyclic Groups
- 非正規(guī)子群彼此同構(gòu)的有限群
- 兩類具有2-等變性的Liénard系統(tǒng)的全局動(dòng)力學(xué)
