EXISTENCE OF SOULUTIONS FOR THE FRACTIONAL (p,q)-LAOLACIAN PROBLEMS INVOLVING A CRITICL SOBLEV EXPNN*
Fanfan CHEN(陳 帆帆) Yang TANG(楊陽)?
School of science,Jiangnan University,Wuxi 214122,China E-mail:1459172465@qq.com;yynjnu@126.com

which can be found in[6]on a bounded domain??RN.On the other hand,the eigenvalue problem for a Laplacian type equation withp=2 was investigated in[12].For the critical(p,q)-Laplacian proble m

wheref(u)is a superlinear continuous function with subcritical growth.It was proved in[1]that problem(1.3)has a nontrivial solution forλsufficiently large.
Recently,equations for a fractional(p,q)-Laplacian operator with critical Sobolev-Hardy exponents have attracted more attention.For instance,authors of[2](see also[21])studied the following problem:

Here,they proved infinitely many weak solutions of the problem(1.5)for some range ofλ,θ.Also,forV(x)≡1,λ=0,and assuming certain other conditions onN,q,r,they proved the existence ofcat?(?)nonnegative solutions by using the Lusternik-Schnirelmann category theory.Later in[16],Goel et al.studied the nonlinear doubly nonlocal equation


We generalize the results of[10]to the fractional(p,q)-Laplacian case.Using the auxiliary functions in[18],we obtain some new asymptotic estimates(see Lemma 2.5).This is also the novelty of this article.The main results of the article are the following:
Theorem 1.1Let 1 (i)N(p?1)/(N?ps1)≤q<(N?ps1)p/N; (ii)N(p?1)/(N?s1) (iii)(1?s1/N)p2s1+ps1 (iv)(p?1)p2s1/(N?ps1) which implies thatu?=0.Thus,u=u+is a critical point ofI(u)and a nonnegative solution of problem(Pμ,λ). This article is organized as follows:in Section 2,we give some notations and preliminaries.Section 3 and Section 4 deal with the proof of Theorem 1.1 and Theorem 1.2,respectively. In this section,we give some valuable results which will be useful in the study of our problem.Fors∈(0,1),we define Denoting byp′=p/(p?1)the H¨older conjugate ofp,|uj(x)?uj(y)|p?2(uj(x)?uj(y))/|x?y|(N+s1p)/p′is bounded inLp′(R2N),and converges to|u(x)?u(y)|p?2(u(x)?u(y))/|x?y|(N+s1p)/p′a.e.in R2N,and(v(x)?v(y))/|x?y|(N+s1p)/p∈Lp(R2N).Therefore,the first integral in(2.4)converges to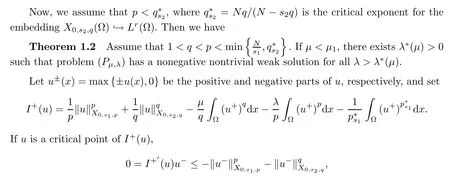
2 Preliminaries








4 Proof of Theorem 1.2

 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
