安徽省樅陽縣宏實中學(xué)(246700) 江保兵

在教學(xué)中,筆者發(fā)現(xiàn)了三角形的一個半角公式,并發(fā)現(xiàn)它們在解題中若能巧妙應(yīng)用,往往可以達(dá)到事半功倍的效果.

設(shè)ΔABC的三邊分別為a,b,c,外接圓和內(nèi)切圓的半徑分別為R,r,面積和半周長分別為S和p,則有:

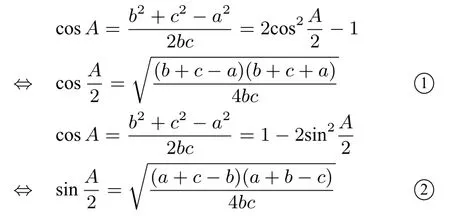
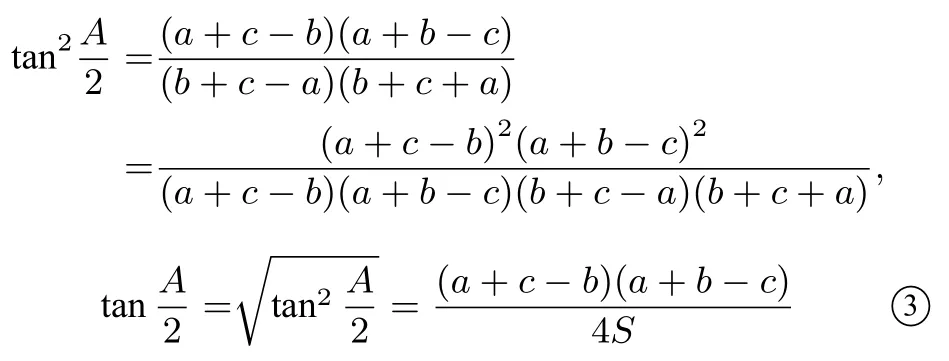
我們把①, ②, ③稱為三角形的半角公式,下面結(jié)合具體的實例,談?wù)勥@三個公式在解題中的應(yīng)用.

例1(《數(shù)學(xué)通報》2020年4月號數(shù)學(xué)問題2536) 設(shè)ΔABC的三內(nèi)角A,B,C所對的三邊分別為a,b,c,三角形面積為Δ,求證: (a+c-b)(a+b-c)+(b+c-a)(b+a-c)+(c+a-b)(c+b-a)≥

證明(a+c-b)(a+b-c),同理:

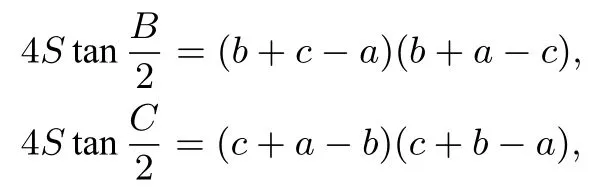
所以待證不等式轉(zhuǎn)化為:

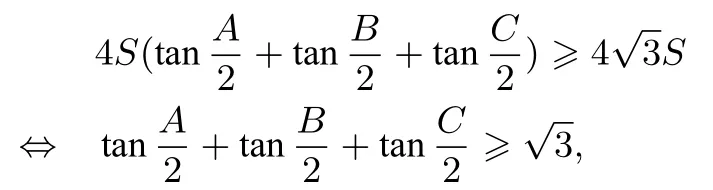
由f(x) =的凹凸性,即原不等式成立,當(dāng)且僅當(dāng)ΔABC為正三角形時,等號成立.

例2(《數(shù)學(xué)通報》2020年7月號數(shù)學(xué)問題2551) 設(shè)ΔABC的面積為S,求證:

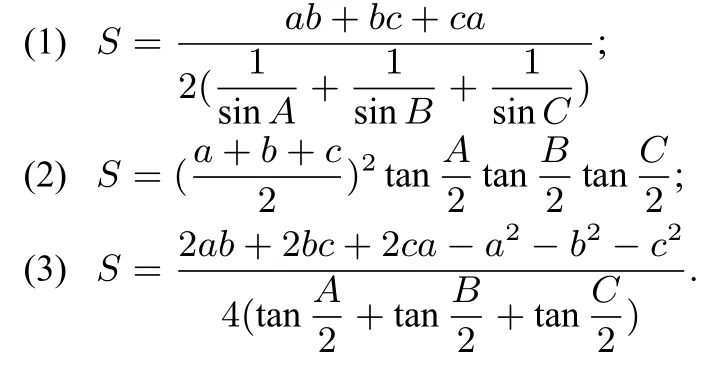
證明(1)略.(2)

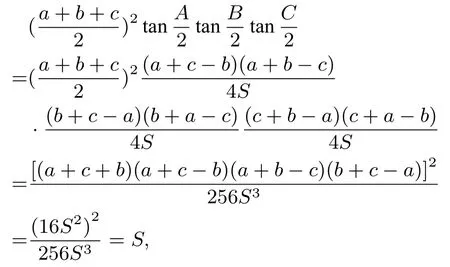
所以原式成立.

(3)由③得到:

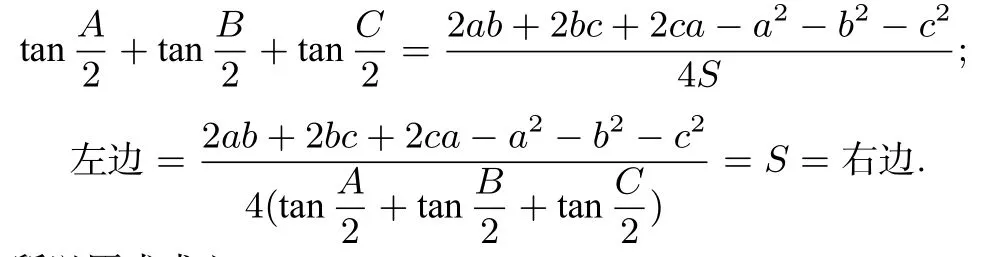
所以原式成立.

上個世紀(jì),美國學(xué)者Jack Garfunkel 在《Crux Mathematicorum》上提出如下猜想(例3),本文利用半角公式,給予一個簡易證明.

例3在ΔABC中, 有

證明一方面,由③得到:

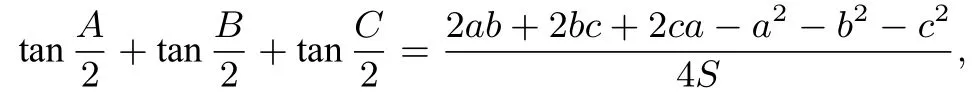
結(jié)合ΔABC中恒等式:

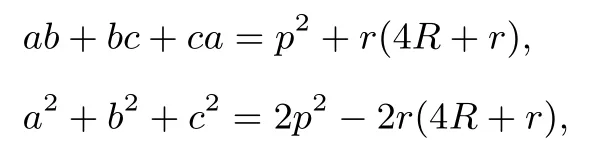
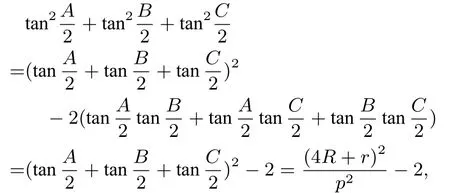
上面化簡過程中用到三角恒等式:

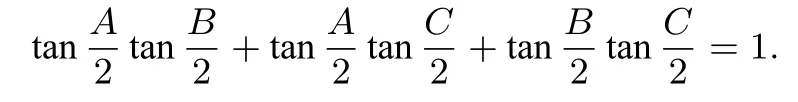
另一方面,

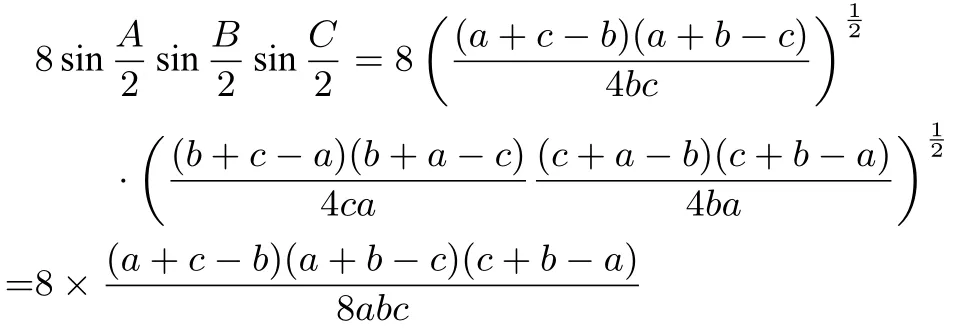
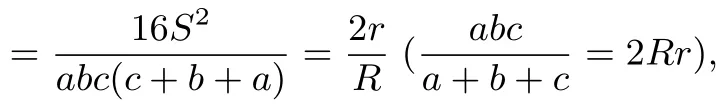
綜合兩方面,欲證

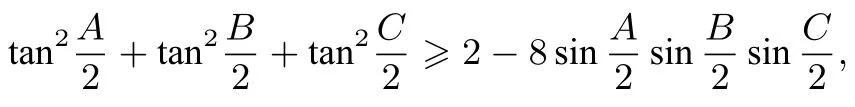
只要證明

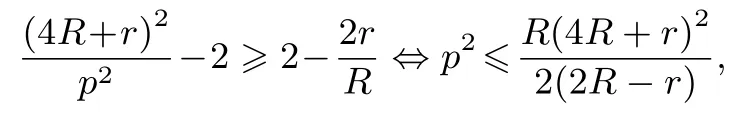
而p2≤即為著名的O.Kooi 不等式, 它是由數(shù)學(xué)家O.Kooi 在1958年發(fā)現(xiàn)并給予證明的, 所以原不等式是成立的, 它是O.Kooi 不等式的一種等價形式, 當(dāng)且僅當(dāng)ΔABC為正三角形時,等號成立.

下面這個例子是例3 的一個變式,證明的過程留給讀者.

例4(《數(shù)學(xué)通報》2019年7月號數(shù)學(xué)問題2439)求證:在ΔABC中,有

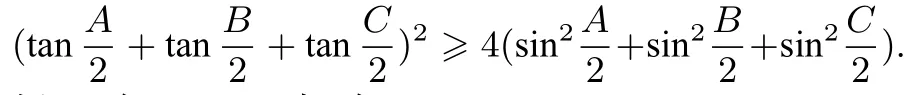
例5在ΔABC中,有

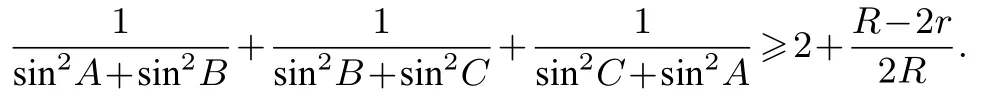
證明

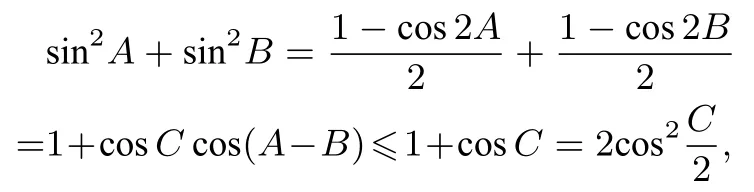
同理,

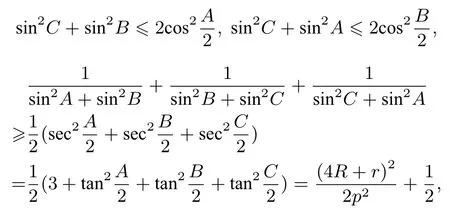
由O.Kooi 不等式p2≤得到:

所以

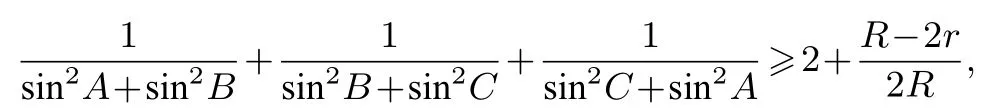
當(dāng)且僅當(dāng)ΔABC為正三角形時,等號成立.