一類(lèi)脈沖微分方程的光滑多尺度解
陳華雄,王巖巖*,劉 偉
(周口師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,河南周口 466000)
§1 引言
許多實(shí)際問(wèn)題往往存在碰撞,開(kāi)關(guān),閾值,脈沖控制和數(shù)字控制等大量的非光滑因素,它們主要是由約束條件,本構(gòu)關(guān)系和控制方式?jīng)Q定的.非光滑因素在現(xiàn)代科技各領(lǐng)域的實(shí)際問(wèn)題中普遍存在,其數(shù)學(xué)模型往往可歸結(jié)為非光滑動(dòng)力系統(tǒng).非光滑動(dòng)力系統(tǒng)近年來(lái)一直受到學(xué)者們的廣泛關(guān)注.從最新的科技成果表明,該類(lèi)系統(tǒng)在控制系統(tǒng),信息科學(xué),生物,材料,管理,航天技術(shù),經(jīng)濟(jì)等各領(lǐng)域中均得到重要的應(yīng)用[1-3].
脈沖微分方程屬于非光滑動(dòng)力系統(tǒng)范疇,是向量場(chǎng)含有瞬時(shí)脈沖作用的動(dòng)力系統(tǒng),是前沿的數(shù)學(xué)分支,其充分考慮到瞬時(shí)突變對(duì)狀態(tài)的影響.因此,該類(lèi)方程具有顯著的特征:脈沖微分方程的解是片段連續(xù)的,不連續(xù)點(diǎn)發(fā)生在瞬時(shí)突變時(shí)刻,即脈沖時(shí)刻.正由于這一特征,使得脈沖微分方程的研究變得豐富,也帶來(lái)了一定的困難.迄今為止,已有諸多的方法用于研究脈沖微分方程解的存在性[4],穩(wěn)定性[5],分支[6]等.
鑒于脈沖微分方程解的不連續(xù)性,文[7]利用奇異攝動(dòng)方法,通過(guò)引入適當(dāng)?shù)钠娈悢z動(dòng)項(xiàng),將脈沖方程的右問(wèn)題擴(kuò)充成具有無(wú)窮大初值的奇異攝動(dòng)問(wèn)題,從而得到連續(xù)的漸近解來(lái)有效地刻畫(huà)原脈沖問(wèn)題的不連續(xù)解.而本文將提供一種以光滑的多尺度解的觀點(diǎn)來(lái)刻畫(huà)脈沖微分方程.通過(guò)引入適當(dāng)?shù)钠娈悢z動(dòng)項(xiàng),不同于文[7],本文定義了一類(lèi)具有臨界情況的奇異攝動(dòng)邊值問(wèn)題,同樣地其對(duì)應(yīng)的退化方程為原脈沖微分方程.利用邊界層函數(shù)法[8]和縫接法[9],構(gòu)造了該奇異攝動(dòng)邊值問(wèn)題的光滑形式多尺度解,并給出了多尺度解的存在性及余項(xiàng)估計(jì).
不失一般性,本文考慮在區(qū)間[0,T]具有一個(gè)脈沖點(diǎn)的脈沖微分方程

為了闡明本文的思想,現(xiàn)引入如下的二階奇攝動(dòng)邊值問(wèn)題
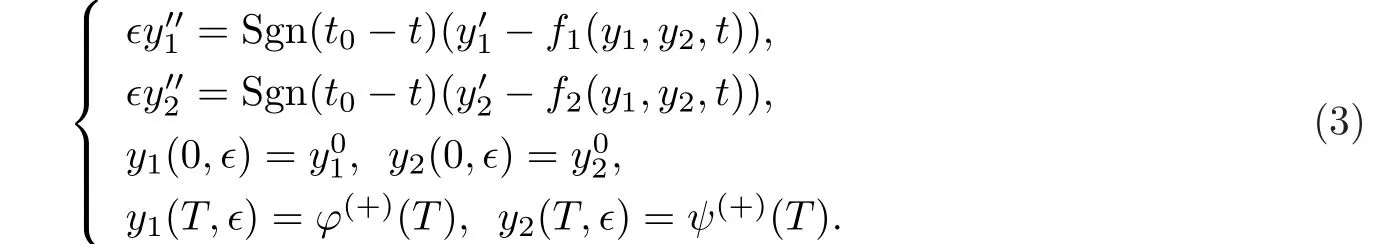
這里0
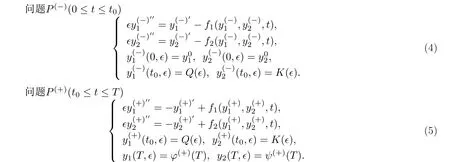
其中,Q(?)=Q0+?Q1+?2Q2+……,K(?)=K0+?K1+?2K2+……,而Qi,Ki為待定參數(shù).
根據(jù)奇異攝動(dòng)理論[8]可知,問(wèn)題(4)和(5)在t=t0處存在邊界層,其對(duì)應(yīng)的退化方程(令?=0)分別為
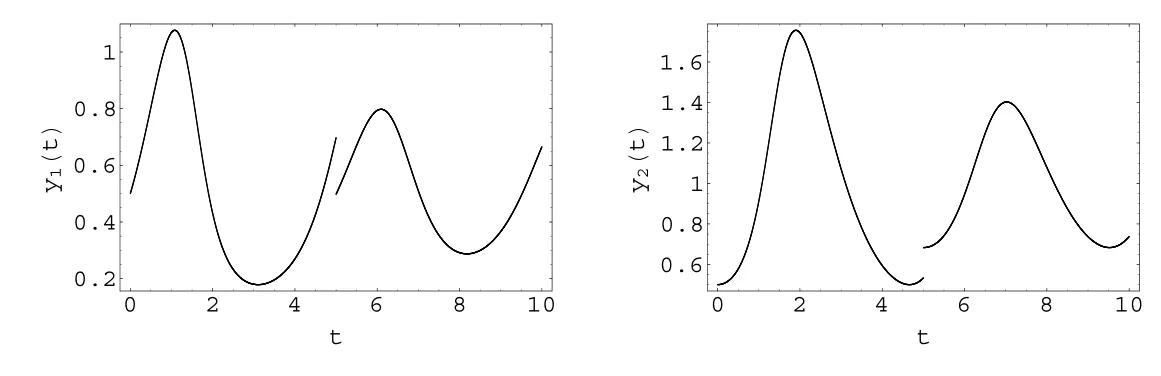
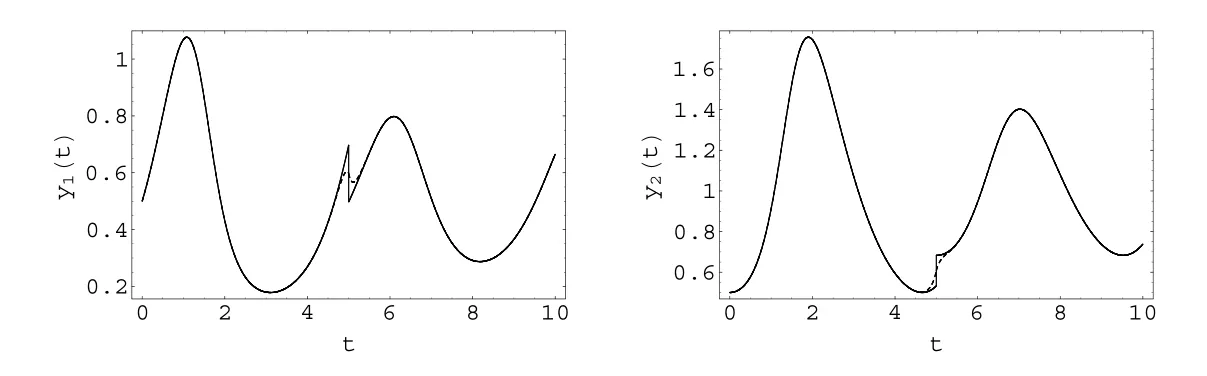
當(dāng)0≤t 當(dāng)t0 比較(2)以及(6)和(7)的解,則問(wèn)題(3)的退化方程的解可視為區(qū)間[0,T]上的脈沖微分方程(1)的解.因此,根據(jù)奇異攝動(dòng)理論[8],當(dāng)?→0時(shí),問(wèn)題(3)的解可有效地刻畫(huà)脈沖微分方程(1)的解. 從(4)和(5)可以看出,問(wèn)題(3)的解在t=t0處是連續(xù)的,為了使其光滑,還需滿(mǎn)足如下條件 這也是確定Qi,Ki的方程. 將問(wèn)題(4)化為如下等價(jià)的方程 則問(wèn)題(9)存在右邊界層,構(gòu)造其如下形式的多尺度解 將(11) 和(12) 代入(9)中,通過(guò)分離變量t和τ后,兩端對(duì)?進(jìn)行冪級(jí)數(shù)展開(kāi)并比較?的同次冪系數(shù),則確定正則級(jí)數(shù)主項(xiàng)所滿(mǎn)足的方程和 以及邊界層項(xiàng)的主項(xiàng)R0zi(τ),R0yi(τ)所滿(mǎn)足的方程 將問(wèn)題(5)化為如下等價(jià)的方程 則問(wèn)題(23)存在左邊界層,構(gòu)造其如下形式的多尺度解 以及邊界層項(xiàng)的主項(xiàng)L0zi(τ),L0yi(τ)所滿(mǎn)足的方程 由光滑性條件(8),可得 (1)Q0,K0的確定 將(15),(16) 和(29),(30) 代入(33),可得 解(36)和(37),得 (2)Qk,Kk的確定 從(21),(22),(31),(32) 以及(34),(35),可得 利用“縫接法”證明問(wèn)題(3)多尺度解的存在性,同時(shí)給出解的漸近表達(dá)式.所求問(wèn)題的多尺度解可以看成兩個(gè)具有純邊界層P(?)和P(+)的解在t=t0處光滑縫接而成. 問(wèn)題P(?)(0≤t ≤t0) 問(wèn)題P(+)(t0≤t ≤T) 可見(jiàn)當(dāng)?充分小,并且取δ為異號(hào)值時(shí),也異號(hào),所以由介值定理,存在Q?∈[Qn?δ,Qn+δ],使得L(Q?,?)=0.同理可證K?的存在性. 定理3.1存在充分小的?0,當(dāng)0 當(dāng)t0≤t ≤T時(shí) 注若在定理3.1 中取i=0,則得到的光滑多尺度解 當(dāng)0≤t ≤t0時(shí) 當(dāng)t0≤t ≤T時(shí) 取?充分小時(shí),則首階多尺度解是脈沖問(wèn)題(1)解的一個(gè)很好的刻畫(huà). 考慮如下具有單個(gè)脈沖點(diǎn)的經(jīng)典的Volterra捕食與被捕食模型 其中,y1(t)表示害蟲(chóng)的種群數(shù)量或種群密度,y2(t) 為天敵的種群數(shù)量或種群密度,a,b,c,d均為正常數(shù),?p1和p2分別表示在t=t0時(shí)刻所噴灑的農(nóng)藥使得害蟲(chóng)的減少量和投放的天敵的數(shù)量. 根據(jù)本文的思想,定義如下的二階非光滑奇異攝動(dòng)邊值問(wèn)題 其中,?(+)(t),ψ(+)(t)為問(wèn)題(38)的解. 為驗(yàn)證本文的結(jié)果,這里取 通過(guò)數(shù)值模擬,從圖1和圖2,可以看出,用本文的方法所構(gòu)造的光滑多尺度解是原脈沖問(wèn)題(38)的一個(gè)很好的刻畫(huà).而?的不同值,則刻畫(huà)了光滑解在脈沖點(diǎn)t=t0處的瞬變程度.?越小,瞬變程度則越厲害. 圖1 原脈沖問(wèn)題(38)的間斷解y1,y2關(guān)于t的圖形 圖2 奇異攝動(dòng)問(wèn)題(39)的首階光滑多尺度解y1,y2關(guān)于t的圖形,其中---, ?=0.1;_____, ?=0.0001 本文說(shuō)明了奇異攝動(dòng)是研究脈沖微分方程的一種有效的方法,它可提供一種以光滑的多尺度解的觀點(diǎn)來(lái)刻畫(huà)原脈沖微分方程,從而為進(jìn)一步揭示脈沖現(xiàn)象提供了嶄新的途徑.在此方法中,重要在于定義對(duì)應(yīng)的奇異攝動(dòng)邊值問(wèn)題.該方法也可以推廣到更復(fù)雜的脈沖微分方程,如依賴(lài)于狀態(tài)的脈沖微分方程等.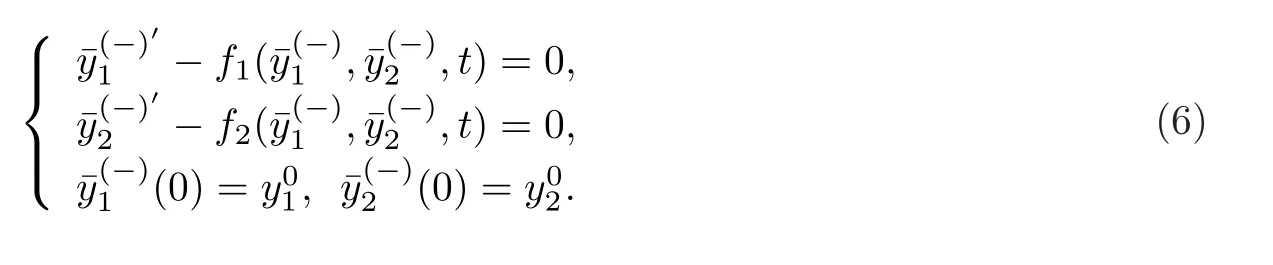
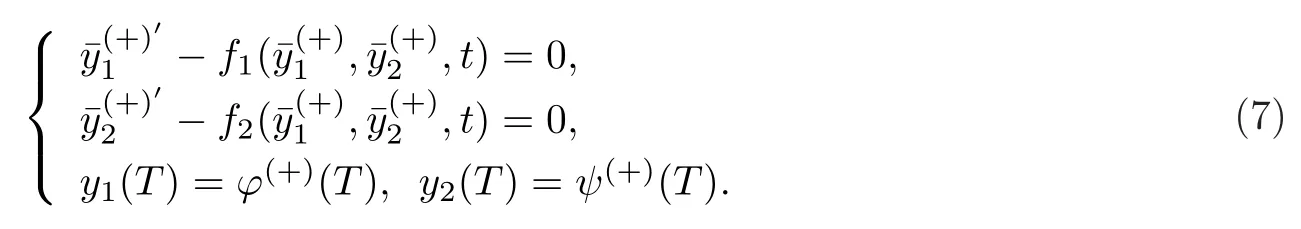
§2 脈沖微分方程及光滑的多尺度解的構(gòu)造

2.1 問(wèn)題P(?)多尺度解的構(gòu)造
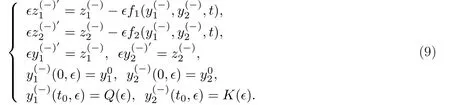
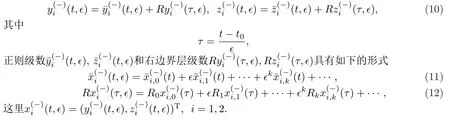
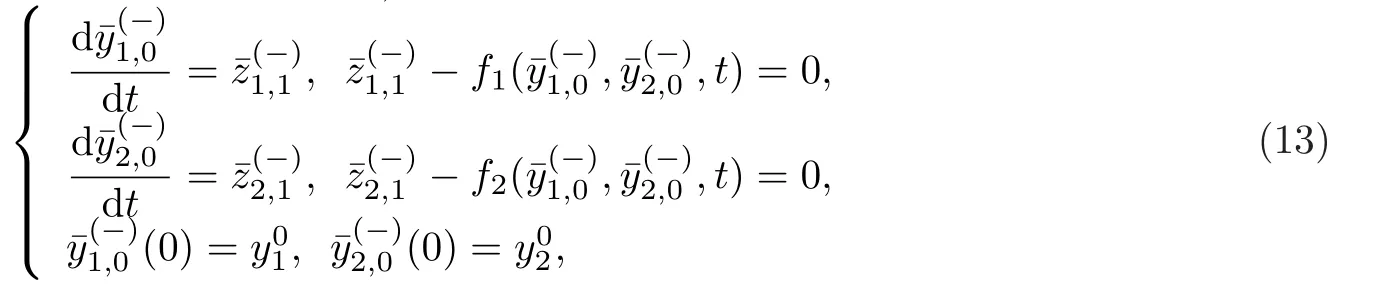


2.2 問(wèn)題P(+)多尺度解的構(gòu)造
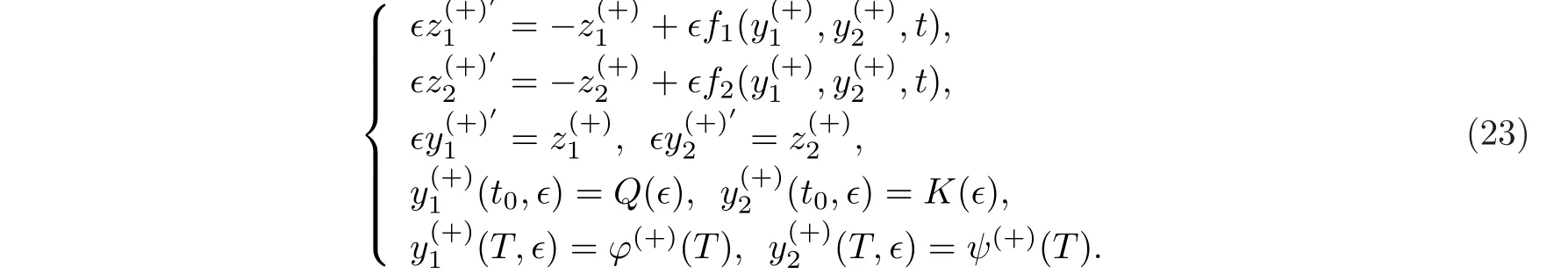

2.3 參數(shù)Qk,Kk的確定
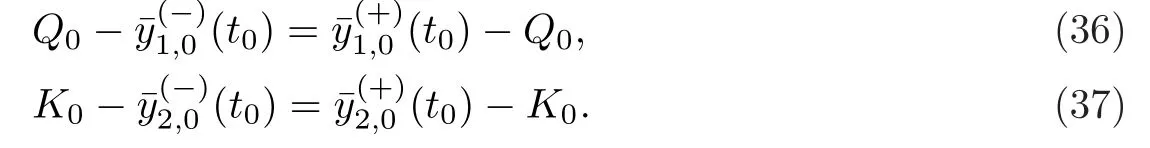
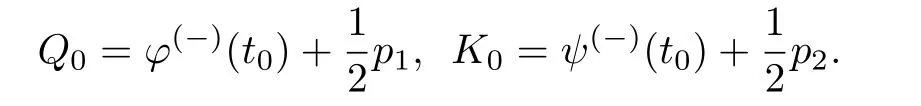
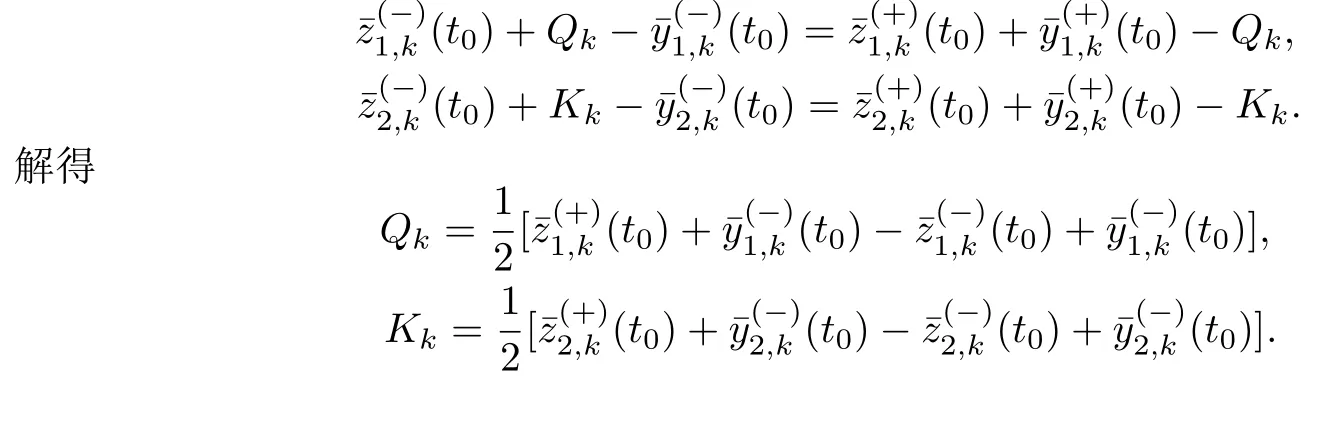
§3 解的存在性與余項(xiàng)估計(jì)
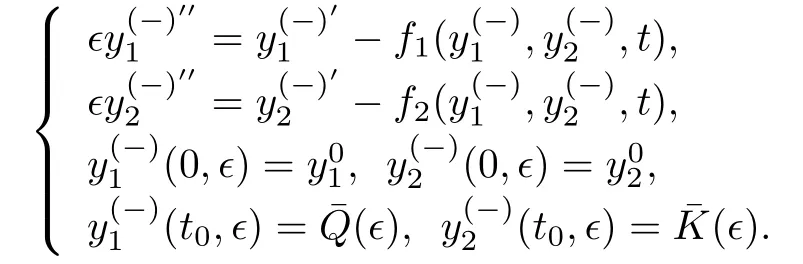
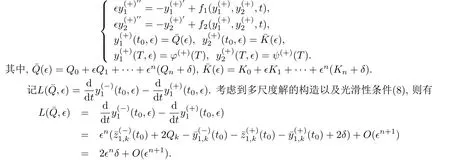

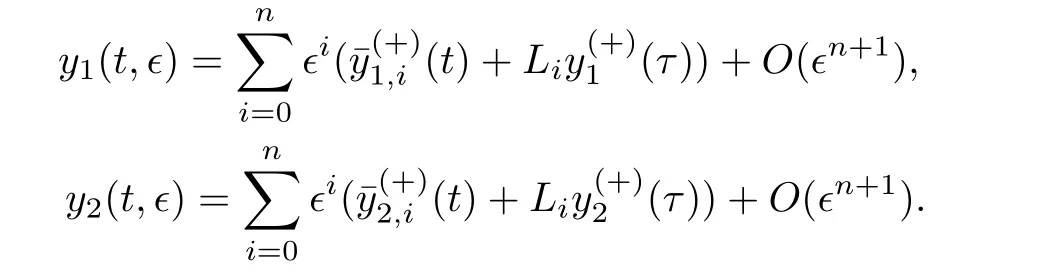
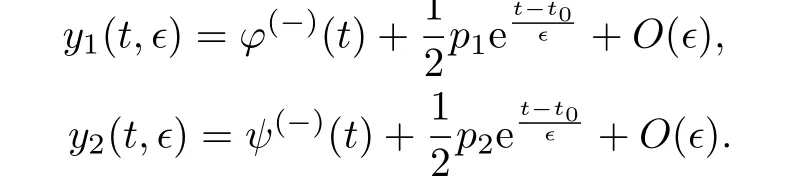
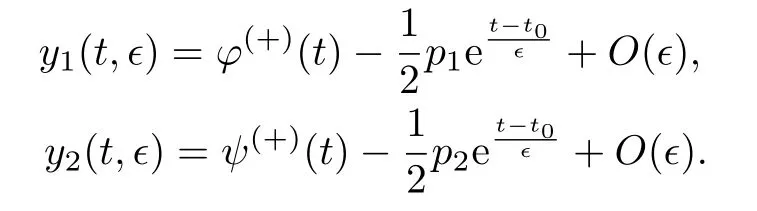
§4 例 子
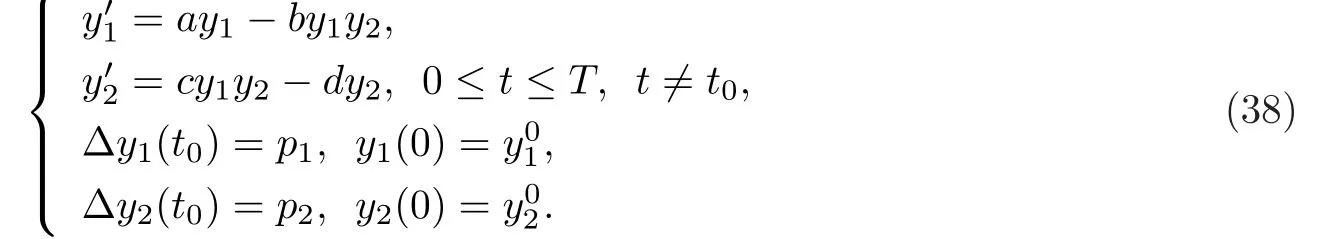
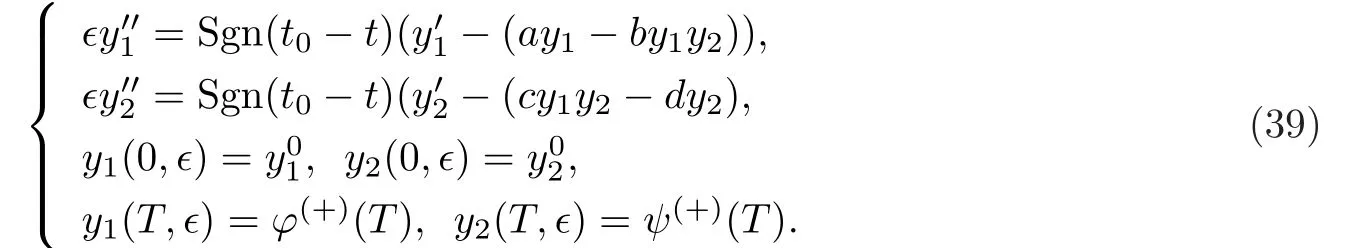
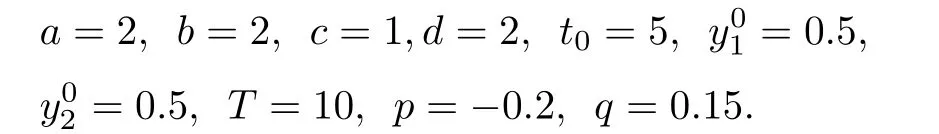
§5 結(jié)論
 高校應(yīng)用數(shù)學(xué)學(xué)報(bào)A輯2021年3期
高校應(yīng)用數(shù)學(xué)學(xué)報(bào)A輯2021年3期
