張麗茹,徐 瑞*

(山西大學復雜系統(tǒng)研究所,山西太原 030006)

§1 引言

人類T細胞白血病或淋巴瘤病毒I型(HTLV-I)是一種在感染者中無限期存在的逆轉(zhuǎn)錄病毒,其感染力弱,并且?guī)缀醪怀霈F(xiàn)在血漿中,通過感染細胞與未感染細胞的直接接觸來傳播病毒.HTLV-I感染者是終身無癥狀攜帶者,其中只有0.25%-3%的感染者會發(fā)展成HAM/TSP,2%-3%的感染者會發(fā)展為ATL,這些患者的外周血中CD8+毒性T淋巴細胞(CTL)的含量很高[1].實驗證明一方面CTL可以降低病毒的載量及清除感染的細胞從而起到保護作用[2-3];但另一方面,CTL含量過高會釋放大量的毒素導致出現(xiàn)HAM/TSP的癥狀,故通過調(diào)節(jié)CTL免疫反應水平可以有效防止HAM/TSP的發(fā)展[4].雖然到目前為止還沒有治愈HTLV-I的方法及中和疫苗,對于HTLV-I相關(guān)疾病的發(fā)病機制也尚未清楚[5],但了解CTL 免疫反應對控制HTLV-I病毒感染具有重要意義.

近幾十年來,對于HTLV-I感染動力學模型的研究引起了很多學者的關(guān)注[6-12].文獻[6]考慮了如下具有CTL免疫反應的HTLV-I感染動力學模型:

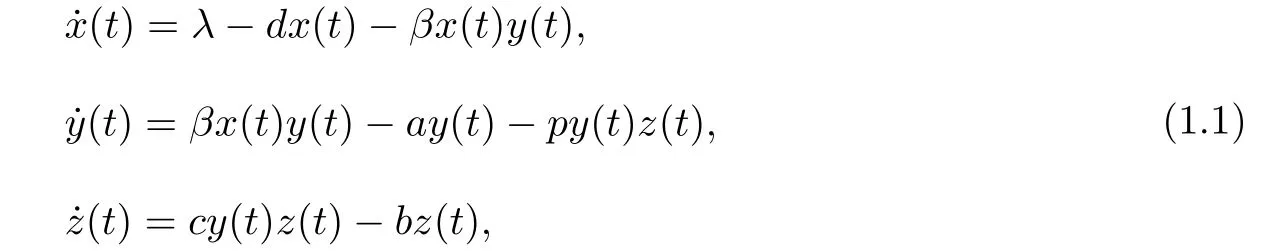
其中x(t),y(t),z(t)分別表示t時刻未感染的CD4+T細胞,感染的CD4+T細胞和CTL免疫細胞的濃度;λ表示未感染的CD4+T細胞的產(chǎn)生率;d,a,b分別表示未感染的CD4+T細胞,感染的CD4+T細胞和CTL免疫細胞的死亡率;βxy表示單位時間內(nèi)新的感染細胞產(chǎn)生的速率;pyz表示通過CTL免疫反應清除感染細胞的速率,cyz表示CTL免疫細胞的生成速率,其參數(shù)值都是正值.

系統(tǒng)(1.1)假定感染過程遵循質(zhì)量作用原理,即感染細胞與未感染細胞之間的感染率是一個常數(shù).文獻[7]通過實驗說明寄生蟲劑量與感染率之間的關(guān)系是非線性的.在文獻[8]中,Song和Neumann指出病毒感染動力學模型中雙線性感染率很難精確描述未感染細胞的感染過程,并提出非線性飽和感染率βxv/(1+αv)來代替質(zhì)量作用感染率.

在實際情況下,HTLV-I是通過感染細胞與未感染細胞的直接接觸來傳播,但接觸時不會立刻被感染,需要經(jīng)過一段時間,因此在模型中考慮胞內(nèi)時滯是很有必要的.Sun和Wei考慮了具有胞內(nèi)時滯的HTLV-I感染模型[9]:

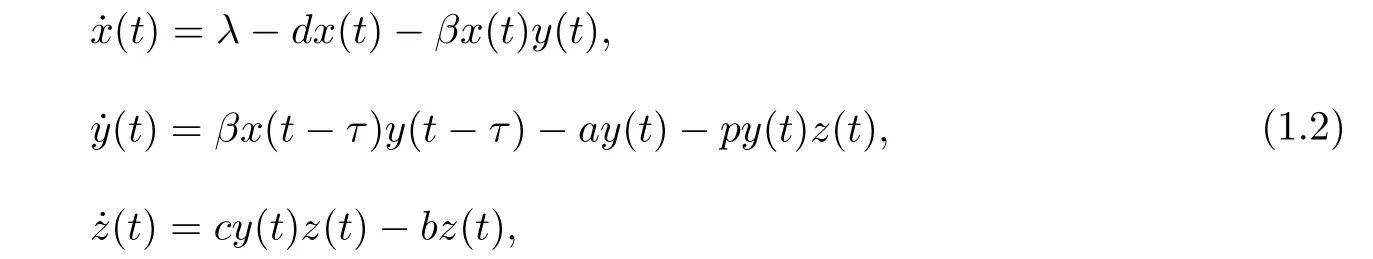
其中τ表示未感染細胞的被感染過程,其主要分為三個階段.第一階段是病毒進入未感染的CD4+T靶細胞后,首先病毒RNA在逆轉(zhuǎn)錄酶抑制劑的作用下逆轉(zhuǎn)錄成病毒DNA,然后病毒DNA 整合到宿主基因組之間的時期;第二階段是進行病毒RNA轉(zhuǎn)錄和病毒蛋白的翻譯的時期;第三階段是病毒釋放并成熟的時期[10].

模型(1.1)和(1.2)均假定CTL免疫細胞的生成速率與感染細胞的濃度成正比.事實上,當感染細胞的濃度達到一定量時,CTL免疫細胞的生成速率不再增加,免疫反應達到飽和狀態(tài).基于以上原因,文獻[11]選取免疫反應函數(shù)為cy(t)z(t)/(z(t)+k),其中k刻畫T細胞被抗原提呈細胞綁定和激活的趨勢[12].

基于文獻[6,9,11]的工作,本文研究胞內(nèi)時滯和飽和CTL免疫反應對HTLV-I感染動力學的影響.為此考慮下列微分方程模型:

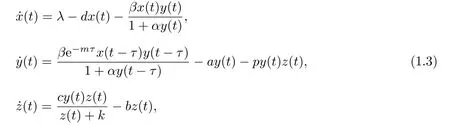
其中e?mτ是感染細胞從時刻t ?τ到時刻t的存活率,其他參數(shù)的生物學意義與模型(1.1)相同.

系統(tǒng)(1.3)滿足如下初始條件:

其中φi(θ)≥0,θ ∈[?τ,0),φi(0)>0,φi(θ)∈C([?τ,0]),這里={(x1,x2,x3) :xi ≥0,i=1,2,3}.由泛函微分方程的基本理論[13]可知系統(tǒng)(1.3)在初始條件(1.4)下的解是唯一的.

定理1.1系統(tǒng)(1.3)在初始條件(1.4)下的解非負且最終有界.

證 反證法.假設t1>0是第一個使得x(t)=0的時刻,則當00,由系統(tǒng)(1.3)的第一個方程可得x′(t1)=λ >0,取充分小的?,在(t1??,t1)上有x(t)≤0,與假設矛盾,故對所有的t>0,都有x(t)>0.

當t ∈[0,τ]時,由系統(tǒng)(1.3)的第二個方程可得

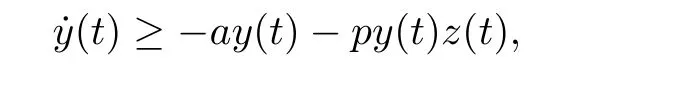
直接求得

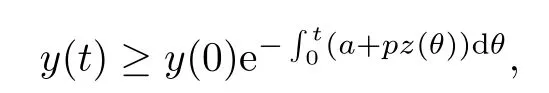
由y(0)>0可知,y(t)>0,t ∈[0,τ].由數(shù)學歸納法可以證明,對所有的t>0,都有y(t)>0.通過系統(tǒng)(1.3)的第三個方程直接計算可得:

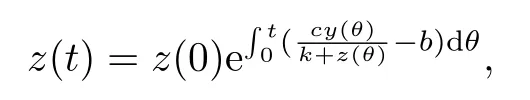
故系統(tǒng)(1.3)的解都是非負的.特別地,如果x(0)>0,y(0)>0,z(0)>0,則(1.3)的解都是正的.

下面證明解的有界性.令:

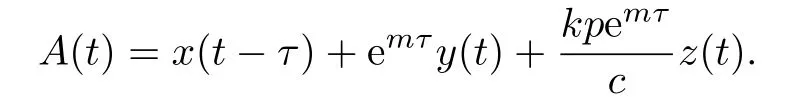
沿著系統(tǒng)(1.3)計算A(t)的全導數(shù)可得:

是系統(tǒng)(1.3)的正不變集.

§2 基本再生數(shù)和可行平衡點

系統(tǒng)(1.3)總存在一個病毒未感染平衡點E0(λ/d,0,0).利用下一代矩陣的方法[19]計算可得系統(tǒng)(1.3)的基本再生數(shù)為

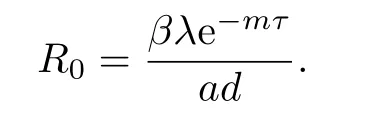
如果R0>1,則系統(tǒng)(1.3)存在一個免疫未激活感染平衡點E1(x1,y1,0),其中

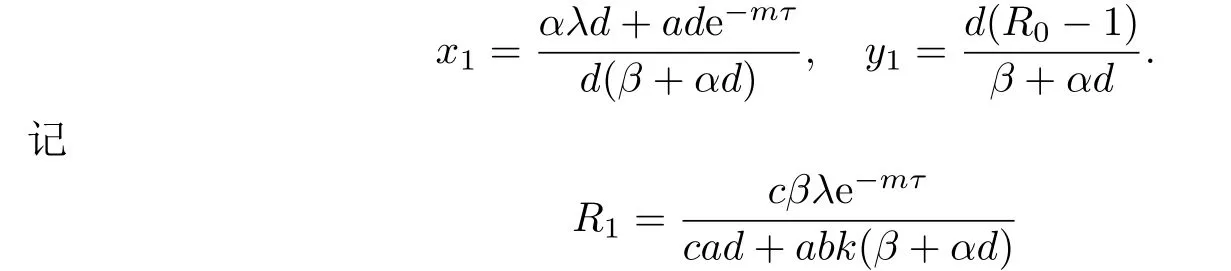
稱R1是免疫反應再生數(shù).易知,當R1>1時,系統(tǒng)(1.3)存在一個免疫激活感染平衡點E2(x2,y2,z2),其中

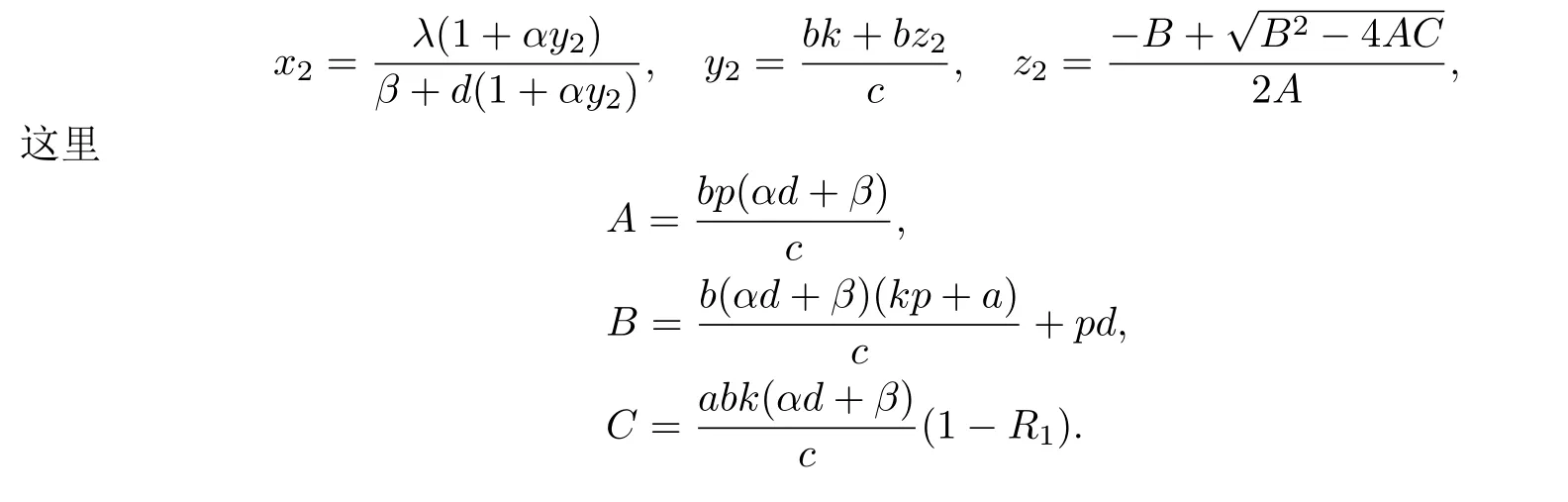
§3 可行平衡點的局部穩(wěn)定性

本節(jié)通過分析相應特征方程根的分布,討論系統(tǒng)(1.3)的可行平衡點的局部穩(wěn)定性.

定理3.1對于系統(tǒng)(1.3),若R0<1,則病毒未感染平衡點E0(λ/d,0,0)是局部漸近穩(wěn)定的,若R0>1,則E0是不穩(wěn)定的.

證系統(tǒng)(1.3)在E0處的特征方程為

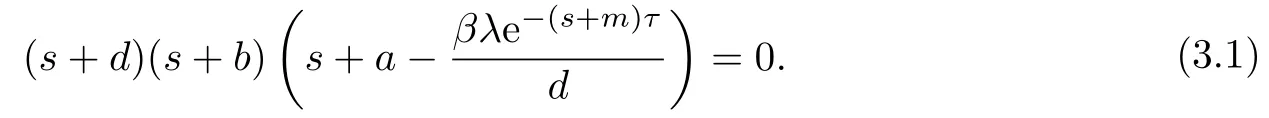
顯然方程(3.1)總有負實根s=?d,s=?b,其他根由方程

確定.

以下證明,當R0<1時,方程(3.2)的根均有負實部.若否,則方程(3.2)存在根s1=a1+ib1,a1≥0.此時有

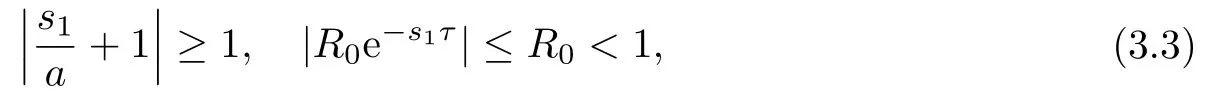
這與(3.2)矛盾.因此若R0<1,則方程(3.1)的所有根均有負實部,從而E0是局部漸近穩(wěn)定的.

當R0>1時,G(s)是關(guān)于s的連續(xù)函數(shù)并且滿足G(0)=1?R0<0,,因此方程(3.1)至少有一個正實根,故E0是不穩(wěn)定的.

定理3.2對于系統(tǒng)(1.3),若R0>1>R1,則免疫未激活感染平衡點E1(x1,y1,0)是局部漸近穩(wěn)定的.

證系統(tǒng)(1.3)在E1處的特征方程是

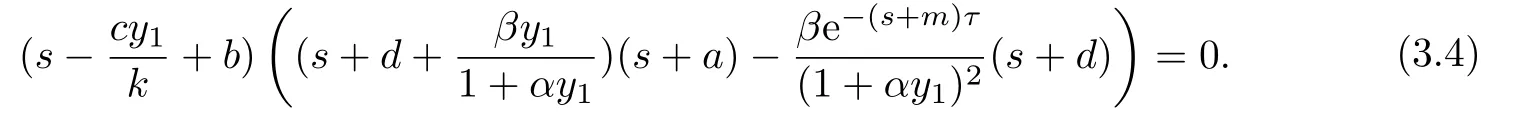
顯然方程(3.4)總有負實根,其他根由以下方程

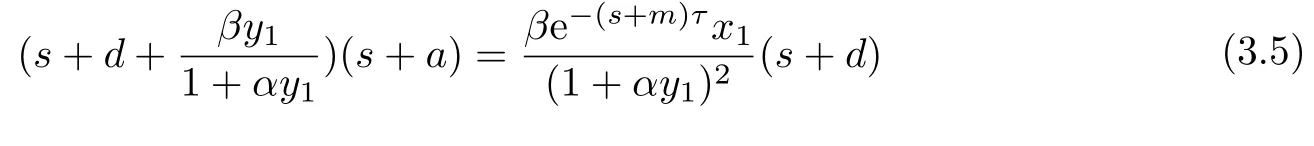
確定.

以下證明,當R0 >1 >R1時,方程(3.5)的根均有負實部.若否,則方程(3.5)存在根s2=a2+ib2，a2 ≥0.此時,有:

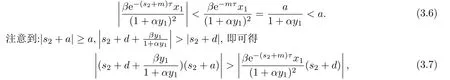
這與(3.5)矛盾.因此,若R0>1>R1,則方程(3.5)的所有根均有負實部,從而E1是局部漸近穩(wěn)定的.

定理3.3對于系統(tǒng)(1.3),若R1>1,則免疫激活感染平衡點E2(x2,y2,z2)是局部漸近穩(wěn)定的.

證系統(tǒng)(1.3)在E2處的特征方程是

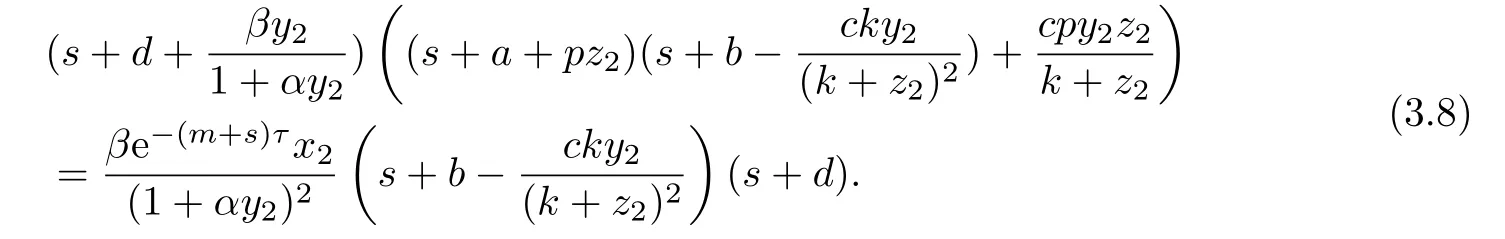
以下證明,當R1>1時,方程(3.8)的根均有負實部.若否,則方程(3.8)存在根s3=a3+ib3,其中a3≥0.此時有

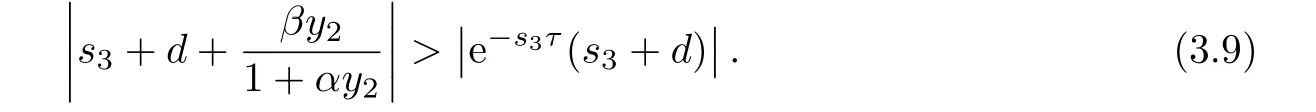
直接計算可得

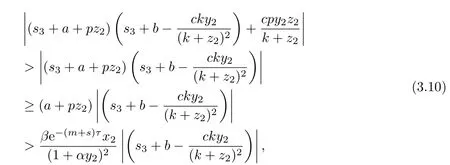
這與(3.8)矛盾.因此若R1>1,則方程(3.8)的所有根均有負實部,從而E2是局部漸近穩(wěn)定的.

§4 可行平衡點的全局漸近穩(wěn)定性

本節(jié)通過構(gòu)造適當?shù)腖yapunov泛函并結(jié)合Lasalle不變性原理來討論系統(tǒng)(1.3)可行平衡點的全局漸近穩(wěn)定性.

定理4.1若R0<1,則系統(tǒng)(1.3)的病毒未感染平衡點E0(λ/d,0,0) 是全局漸近穩(wěn)定的.

證設(x(t),y(t),z(t))是系統(tǒng)(1.3)在初始條件(1.4)下的任意正解,定義

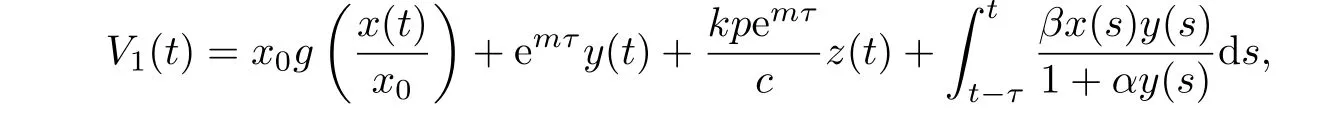
其中g(shù)(x)=x ?1?lnx.顯然g(x)>0,x/=1,g(1)=0.

沿著系統(tǒng)(1.3)計算V1(t)的全導數(shù)可得

定理4.2若R0>1>R1,則系統(tǒng)(1.3)的免疫未激活感染平衡點E1(x1,y1,0)是全局漸近穩(wěn)定的.

定理4.3若R1>1,則系統(tǒng)(1.3)的免疫激活感染平衡點E2(x2,y2,z2)是全局漸近穩(wěn)定的.

沿著系統(tǒng)(1.3)計算V3(t)的導數(shù)可得

§5 敏感性分析

本節(jié)對病毒感染再生數(shù)和免疫反應再生數(shù)進行敏感性分析.在系統(tǒng)(1.3)中,相應的參數(shù)取值如表1所示.

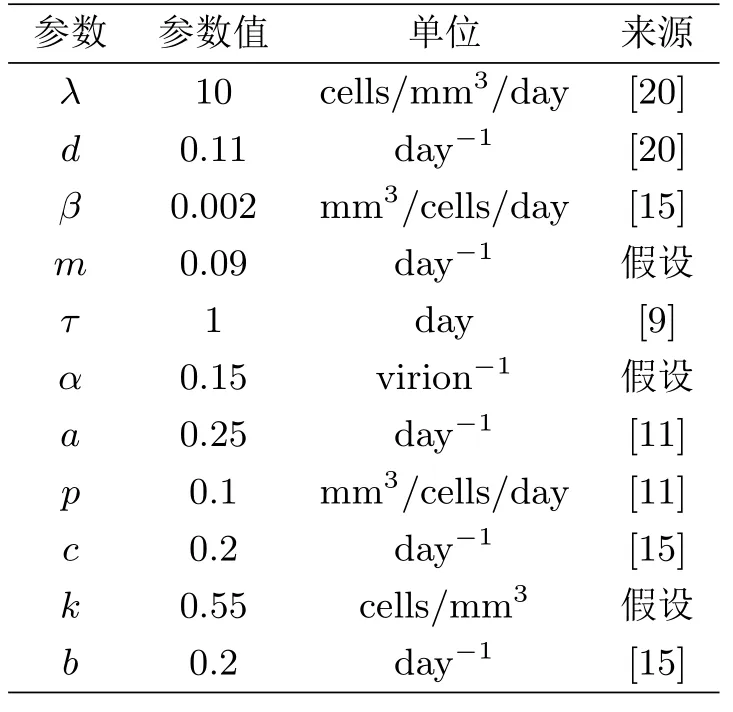
表1 系統(tǒng)(1.3)的參數(shù)取值

敏感性分析用于量化再生數(shù)的變量范圍,并確定引起再生數(shù)變化的關(guān)鍵因素.近年來,拉丁超立方抽樣被證明是一種更有效的統(tǒng)計抽樣技術(shù),已被引入疾病建模領(lǐng)域[21].文獻[22]指出偏執(zhí)相關(guān)系數(shù)提供了參數(shù)和再生數(shù)之間線性關(guān)聯(lián)強度的度量.偏執(zhí)相關(guān)系數(shù)的正負分別表示參數(shù)與再生數(shù)的正相關(guān)或負相關(guān),其大小衡量了這種相關(guān)性的強度.因此,為了對病毒感染再生數(shù)和免疫反應再生數(shù)進行敏感性分析,先利用拉丁超立方抽樣對參數(shù)空間進行抽樣,再計算偏執(zhí)相關(guān)系數(shù).由圖1(a)可知,對于病毒感染再生數(shù)R0,λ,β是正相關(guān)變量,m,τ,d,a是負相關(guān)變量,按相關(guān)強度順序依次是:λ,β,d,a,m,τ;由圖1(b)可知,對于免疫反應再生數(shù)R1,λ,β,c是正相關(guān)變量,m,τ,α,d,a,k,b是負相關(guān)變量,按相關(guān)強度順序依次是λ,β,d,a,k,τ,m,c,α,b.

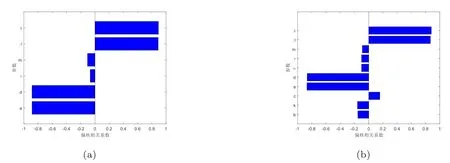
圖1 病毒感染再生數(shù)R0和免疫反應再生數(shù)R1的敏感性分析

§6 結(jié)論

本文研究了一類具有胞內(nèi)時滯,飽和感染率及飽和CTL免疫反應的HTLV-I感染動力學模型.通過嚴格的數(shù)學分析,建立了系統(tǒng)(1.3)的闕值動力學.通過構(gòu)造適當?shù)腖ypunov泛函,證明了病毒未感染平衡點E0,免疫未激活感染平衡點E1和免疫激活感染平衡點E2的全局穩(wěn)定性由病毒感染再生數(shù)R0和免疫反應再生數(shù)R1的值完全決定:當R0<1時,未感染平衡點E0全局漸近穩(wěn)定,病毒被清除;當R0>1>R1時,免疫未激活感染平衡點E1全局漸近穩(wěn)定,感染持續(xù)但免疫未被激活;當R1>1時,免疫激活感染平衡點E2全局漸近穩(wěn)定,HTLV-I進入慢性感染期.