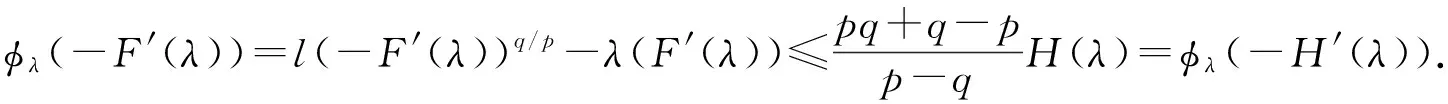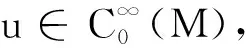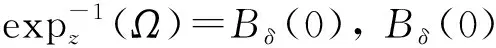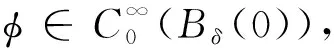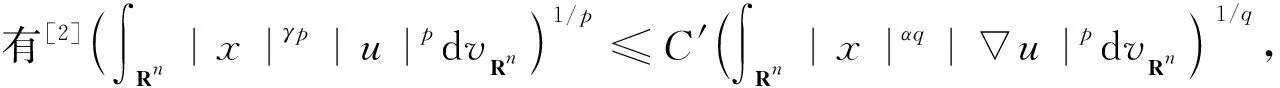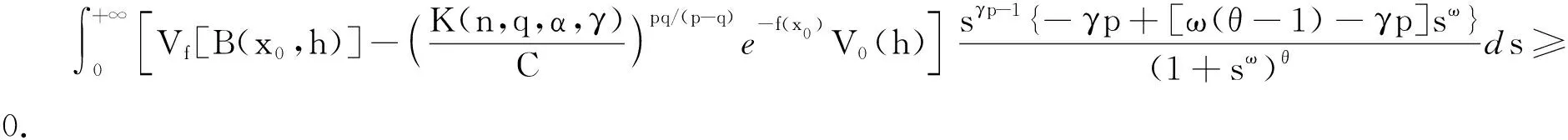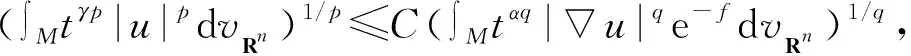鄧嚴(yán)林, 侯蘭寶*, 杜 鋒, 嚴(yán) 政

(1. 荊楚理工學(xué)院數(shù)理學(xué)院, 湖北 荊門 448000; 2. 湖北大學(xué)應(yīng)用數(shù)學(xué)湖北省重點實驗室, 武漢 430062;3. 長江大學(xué)信息與數(shù)學(xué)學(xué)院, 湖北 荊州 434023)

泛函不等式是微分幾何研究的重要問題, 當(dāng)某些黎曼流形上的泛函不等式成立時, 則其一些幾何性質(zhì)將與歐氏空間產(chǎn)生聯(lián)系．Adrinao等[1]證明了: 當(dāng)M是一個具有漸近非負(fù)Ricci曲率的完備非緊黎曼流形時, 若M上權(quán)重Sobolev不等式成立, 則M接近于相應(yīng)維數(shù)的歐氏空間, 這里的接近是指M上半徑為r的測地球的體積和相同維數(shù)歐氏空間中半徑為r的球的體積接近, 而由體積比較定理可知, 此時M與相同維數(shù)歐氏空間接近等距; Barbosa等[2]則研究了一類具有非負(fù)Ricci曲率的完備非緊黎曼流形上的二階Sobolev不等式, 給出了一些滿足非坍塌體積條件下流形的剛性結(jié)果．近年來,關(guān)于泛函不等式的研究已在更為廣泛的幾何空間中展開．Balogh等[3]研究了Heisenberg群上一些泛函不等式, 給出了次黎曼版的Borell-Brascamp-Lieb 不等式; Du等[4]研究了度量測度空間上的Hardy不等式; Mao[5]研究了光滑度量測度空間上的Gagliardo-Nirenberg 不等式; Kristly[6]研究非光滑度量測度空間上的Gagliardo-Nirenberg 不等式, 給出了相關(guān)的剛性結(jié)論; Duy等[7]研究了具有非徑向重量的Hardy 型和Caffarelli-Kohn-Nirenberg型不等式; Huang等[8]研究了Finsler流形上的泛函不等式; Mai等[9]研究了完備收縮Ricci孤立子上的泛函不等式．綜上所述, 本文擬將文獻(xiàn)[1]的結(jié)論推廣到具有非負(fù)Bakry-émery Ricci曲率的完備非緊光滑度量測度空間．

1 基本概念與預(yù)備知識

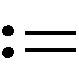
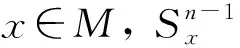
對于一個固定向量ξ∈TxM, |ξ|=1, 設(shè)ξ⊥是{Rξ}在TxM中的正補交, 則τt:TxM→Texpx(tξ)M是沿著γξ(t)的平行變換．設(shè)Yη(t)=d(expx)(tξ)(tη)是沿著γξ(t)的Jacobi場, 且滿足Yη(0)=0和(tYη)(0)=η, 則映射A(t,ξ):ξ⊥→ξ⊥可定義為A(t,ξ)η=(τt)-1Yη(t), 表示線性變換的路徑．

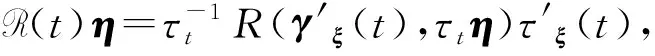
ds2(expx(tξ))=dt2+|A(t,ξ)dξ|2,?tξ∈Dx．

(1)

定義DxC(x)上的正函數(shù)

(2)

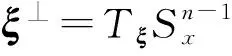
(3)

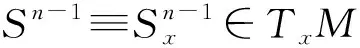
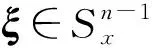
(4)

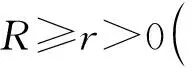
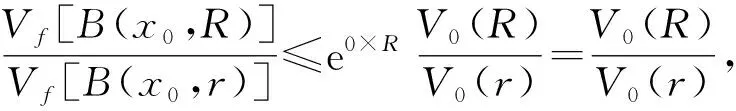
(5)

因此, 如果?tf≥0和Ricf≥0, 有

Vf[B(x0,R)]≤e-f(x0)·V0(R),R>0．

(6)

2 主要結(jié)果及證明

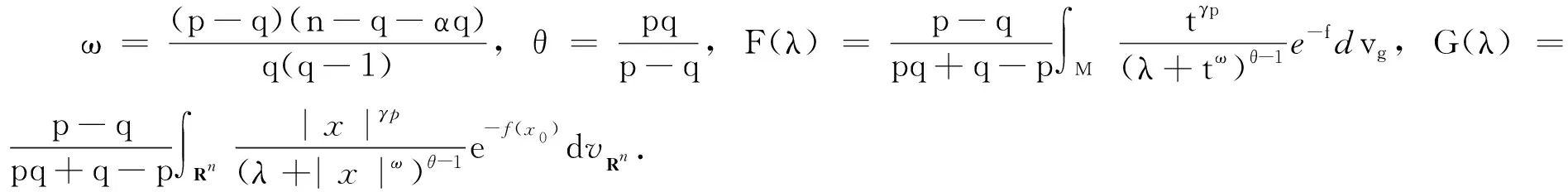
引理2設(shè)p,q,α和γ是常數(shù), 且滿足

1

(7)

(8)

由式(7), 得ω>0,n+γp-1>-1,n+γp-1-ωθ<-1,n+γp-α-ωθ+ω<-1．由0≤F(λ)<+∞(?λ>0)及F是明確的和可微的,有

(9)

(10)

(11)

定義函數(shù)H(λ)=Bλ1-q/p,λ∈[0,+∞)．由

(12)

(13)

下證:“如果對于一個常數(shù)λ0>0, 有F(λ0)=H(λ0), 那么對于所有的λ<λ0, 有F(λ)=H(λ)．”

證明 使用反證法．定義λ1=sup{λ<λ0;F(λ)≥H(λ)}, 則對于任意的λ∈[λ1,λ0], 有0

(14)

因為對于常數(shù)λ0>0, 有F(λ0)0．命題得證．

注如果q=2,1-n/2<α≤0,α-1<γ≤α, 權(quán)重Sobolev不等式中的常數(shù)不小于相同維數(shù)歐氏空間中權(quán)重Sobolev不等式的最優(yōu)常數(shù)．

(1-ε)2δij≤e-(n-1)f(x0)gij≤(1+ε)2δij．

(15)

ii) 因C≥K(n,q,α,γ), 則可以將證明分以下兩種情形討論．

(16)