呂永峰 ,田建艷 ,菅 壟 ,任雪梅

(1.太原理工大學(xué)電氣與動(dòng)力工程學(xué)院,山西太原 030024;2.北京理工大學(xué)自動(dòng)化學(xué)院,北京 100081)

1 引言

近似動(dòng)態(tài)規(guī)劃方法(approximate dynamic programming,ADP)作為一種新型有效的最優(yōu)控制求解方法,已經(jīng)得到了廣泛的研究[1–2].在強(qiáng)化學(xué)習(xí)(reinforcement learning,RL)算法的基礎(chǔ)上,Werbos[3]首次提出近似動(dòng)態(tài)規(guī)劃方法用于求解離散時(shí)間系統(tǒng)的最優(yōu)控制問(wèn)題.近年來(lái),這種方法得到進(jìn)一步的發(fā)展,可以近似地求解連續(xù)系統(tǒng)的動(dòng)態(tài)規(guī)劃最優(yōu)控制問(wèn)題,為未知非線(xiàn)性系統(tǒng)實(shí)時(shí)在線(xiàn)的最優(yōu)控制求解提供了一種有效的解決方案[4–6].但是現(xiàn)有基于近似動(dòng)態(tài)規(guī)劃的研究大多只用于求解無(wú)擾動(dòng)系統(tǒng)的最優(yōu)控制[7–10]或最優(yōu)跟蹤控制問(wèn)題[11–15],也得到許多推廣應(yīng)用研究[16–17],比如制導(dǎo)[16],電網(wǎng)能源管理控制[18]等.

在實(shí)際工程中,系統(tǒng)通常會(huì)受到未知干擾,需要設(shè)計(jì)H∞控制器,它可以看作是一個(gè)兩人零和博弈模型[19–21],這一問(wèn)題在過(guò)去幾年得到廣泛的研究[22].學(xué)者們提出許多控制方案[19,23–24]通過(guò)獲得預(yù)定性能指標(biāo)的鞍點(diǎn)獲得線(xiàn)性和非線(xiàn)性系統(tǒng)的H∞控制.一般來(lái)說(shuō),H∞控制器需要求解非線(xiàn)性系統(tǒng)的Hamilton–Jacobi–Isaacs(HJI)方程和線(xiàn)性系統(tǒng)的代數(shù)黎卡提方程[25].然而,由非線(xiàn)性系統(tǒng)導(dǎo)出的HJI方程是一個(gè)非線(xiàn)性偏微分方程,當(dāng)系統(tǒng)較大時(shí)會(huì)出現(xiàn)“維數(shù)災(zāi)難”問(wèn)題而難以求解[26].為了解決這一難題,學(xué)者們應(yīng)用近似動(dòng)態(tài)規(guī)劃方法學(xué)習(xí)H∞控制[27].張等[28]、Abu Khalaf等[29]利用離線(xiàn)迭代強(qiáng)化學(xué)習(xí)算法得到H∞控制器;文獻(xiàn)[19]提出在線(xiàn)同步強(qiáng)化學(xué)習(xí)算法解決這一問(wèn)題.然而,這些方法要求系統(tǒng)動(dòng)態(tài)完全已知,李等在文獻(xiàn)[30]中使用積分強(qiáng)化學(xué)習(xí)算法學(xué)習(xí)動(dòng)態(tài)未知線(xiàn)性系統(tǒng)HJI方程的解.文獻(xiàn)[29]進(jìn)一步提出高效的異步策略強(qiáng)化學(xué)習(xí)算法學(xué)習(xí)HJI方程的解.

但是上述H∞控制大部分只涉及單輸入系統(tǒng),并未考慮多輸入系統(tǒng).現(xiàn)有針對(duì)多輸入系統(tǒng)的研究大部分僅僅基于非零和博弈求解最優(yōu)控制,并未考慮系統(tǒng)外部干擾[4,31].少數(shù)涉及多輸入系統(tǒng)或者多智能體H∞控制的研究成果[32–33],文獻(xiàn)[32]求解多智能體的H∞控制,其中每個(gè)智能體涉及一個(gè)外部擾動(dòng);文獻(xiàn)[33]雖然求解混合博弈下多輸入系統(tǒng)的均衡解,卻只考慮最后一個(gè)輸入的抗干擾性能;文獻(xiàn)[24]應(yīng)用Q學(xué)習(xí)方法設(shè)計(jì)線(xiàn)性多輸入系統(tǒng)的H∞控制,但未考慮非線(xiàn)性多輸入系統(tǒng).非線(xiàn)性多輸入系統(tǒng)的抗干擾控制具有許多工程應(yīng)用,比如多驅(qū)動(dòng)負(fù)載系統(tǒng),機(jī)械臂系統(tǒng)和許多其他的工控系統(tǒng)[24].因此針對(duì)多輸入非線(xiàn)性系統(tǒng)的H∞控制研究具有重要意義.總之,先前研究成果大部分使用標(biāo)準(zhǔn)的執(zhí)行–評(píng)價(jià)ADP結(jié)構(gòu),而且并未考慮多輸入系統(tǒng)的H∞控制器設(shè)計(jì).因此針對(duì)受外部干擾的多輸入非線(xiàn)性系統(tǒng),ADP方法的實(shí)現(xiàn)仍然會(huì)面對(duì)很大挑戰(zhàn).

針對(duì)以上所述現(xiàn)存關(guān)于多輸入受干擾非線(xiàn)性系統(tǒng)的H∞控制問(wèn)題,本文提出一種改進(jìn)的在線(xiàn)ADP方法求解動(dòng)態(tài)部分未知多輸入非線(xiàn)性連續(xù)系統(tǒng)的H∞控制.在該方案中,避免了文獻(xiàn)[8]中的執(zhí)行神經(jīng)網(wǎng)絡(luò),從而簡(jiǎn)化ADP框架.此外,還應(yīng)用一種新的自適應(yīng)律[28]在線(xiàn)更神經(jīng)網(wǎng)絡(luò)權(quán)重.引入評(píng)價(jià)神經(jīng)網(wǎng)絡(luò)在線(xiàn)學(xué)習(xí)HJI方程的解(即最優(yōu)的性能指標(biāo)函數(shù)),利用逼近的神經(jīng)網(wǎng)絡(luò)計(jì)算多輸入系統(tǒng)H∞控制.最后,證明在所設(shè)計(jì)H∞控制作用下閉環(huán)系統(tǒng)的穩(wěn)定性,并保證近似的H∞控制收斂到最優(yōu)策略附近的緊集.仿真結(jié)果驗(yàn)證了所提方法的有效性.

2 多輸入系統(tǒng)H∞控制問(wèn)題描述

考慮以下帶干擾的多輸入非線(xiàn)性系統(tǒng):

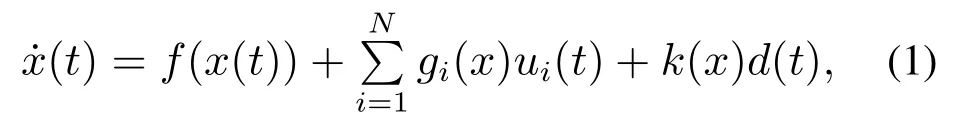
其中:x ∈Rn為系統(tǒng)狀態(tài),ui ∈Rmi(i=1,···,N)表示N個(gè)系統(tǒng)輸入,d ∈Rq為系統(tǒng)有界未知的外部干擾.f(x)∈Rn系統(tǒng)非線(xiàn)性動(dòng)態(tài),gi(x)∈Rn×mi和k(x)∈Rn×q分別表示系統(tǒng)輸入動(dòng)態(tài)和干擾動(dòng)態(tài).假設(shè)f(0)=0,且f(x)+gi(x)ui(t)+k(x)d(t)在實(shí)數(shù)集Ω上Lipschitz連續(xù)且穩(wěn)定.

本文結(jié)合二人零和微分博弈理論[18]求解多輸入非線(xiàn)性系統(tǒng)的H∞控制,其中求解的控制ui(t)要最小化給定多輸入系統(tǒng)的性能指標(biāo),求解的干擾d(t)為使性能指標(biāo)最壞的情況下的外部干擾,即控制對(duì)()滿(mǎn)足零和博弈下的鞍點(diǎn)平衡條件.在求解到最壞的干擾之后,多輸入系統(tǒng)的H∞控制器ui(t)各參數(shù)已經(jīng)調(diào)整到相應(yīng)的值,在之后系統(tǒng)受到未知的外部干擾,能使性能指標(biāo)的值更小,從而更加滿(mǎn)足H∞性能指標(biāo)條件.多輸入非線(xiàn)性系統(tǒng)的H∞性能指標(biāo)定義為

需要指出,本文所提方法適用于多輸入系統(tǒng)具有一個(gè)H∞性能指標(biāo)的情況.當(dāng)多輸入系統(tǒng)每個(gè)輸入都具有一個(gè)H∞性能指標(biāo)時(shí),需要應(yīng)用更加復(fù)雜的方法進(jìn)行求解.

最優(yōu)的性能指標(biāo)函數(shù)表示為[34–35]

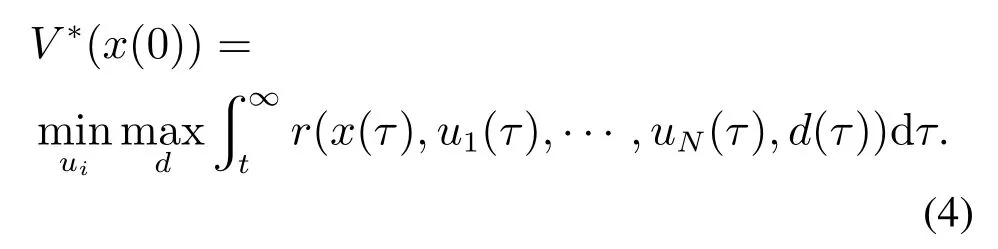
假設(shè)以上性能指標(biāo)的鞍點(diǎn)存在,則系統(tǒng)(1)存在唯一的一組H∞控制[36].為了獲得H∞控制器,哈密爾頓函數(shù)給定為

給出以下引理[34–35].

引理11)如果衰減因子γ ＞0,V(x):Rn →R光滑連續(xù),則V *(x)≥0是HJI方程(8)的最優(yōu)解.2)如果系統(tǒng)(1)狀態(tài)可觀,則所求得的最優(yōu)H∞控制(t)和d*(t)滿(mǎn)足性能指標(biāo)函數(shù)(4),且()為在[L2,∞)上的鞍點(diǎn),能使多輸入非線(xiàn)性系統(tǒng)(1)穩(wěn)定.

注1不同于一般的最優(yōu)控制,H∞控制要求在鞍點(diǎn)存在的情況下得到性能指標(biāo)函數(shù)的鞍點(diǎn),在系統(tǒng)受到其他外部干擾時(shí),能夠使系統(tǒng)狀態(tài)穩(wěn)定且滿(mǎn)足H∞性能指標(biāo),具有較強(qiáng)的抗干擾能力.為了避免直接求解HJI方程,本文使用神經(jīng)網(wǎng)絡(luò)逼近性能指標(biāo)函數(shù),避免了文獻(xiàn)[27]中的執(zhí)行結(jié)構(gòu),優(yōu)化了近似動(dòng)態(tài)規(guī)劃方法.

3 多輸入系統(tǒng)H∞控制設(shè)計(jì)

先前研究成果[37]應(yīng)用執(zhí)行–評(píng)價(jià)神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)求解非線(xiàn)性系統(tǒng)的H∞控制對(duì)(u*,d*),d*表示使給定性能指標(biāo)表現(xiàn)情況最壞的外部擾動(dòng),如伺服系統(tǒng)運(yùn)行過(guò)程中使給定性能指標(biāo)函數(shù)最大的外部力矩,飛行器飛行過(guò)程中的風(fēng)力擾動(dòng)和機(jī)械臂運(yùn)行過(guò)程中的未知外部阻力等,其中神經(jīng)網(wǎng)絡(luò)權(quán)值使用最小二乘法或迭代自適應(yīng)算法更新.本文提出一種新的自適應(yīng)神經(jīng)網(wǎng)絡(luò)逼近最優(yōu)性能指標(biāo)函數(shù),直接用于多輸入系統(tǒng)H∞控制的求解,避免了在設(shè)計(jì)H∞控制器過(guò)程中使用執(zhí)行神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu).并利用基于估計(jì)誤差的自適應(yīng)律估計(jì)性能指標(biāo)的神經(jīng)網(wǎng)絡(luò)權(quán)值,在線(xiàn)計(jì)算出多輸入系統(tǒng)最優(yōu)H∞控制().

3.1 近似動(dòng)態(tài)規(guī)劃神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)

為了設(shè)計(jì)H∞控制式(6)和式(7),需要求解非線(xiàn)性的HJI方程(8)獲得最優(yōu)的值函數(shù)V *(x).因?yàn)榉蔷€(xiàn)性HJI方程(8)難以求解,所以使用神經(jīng)網(wǎng)絡(luò)逼近最優(yōu)的性能指標(biāo)函數(shù)V *(x).假設(shè)性能指標(biāo)函數(shù)V *(x)在實(shí)數(shù)集Ω上光滑連續(xù),則可用單層神經(jīng)網(wǎng)絡(luò)逼近為

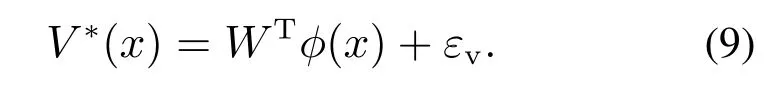
其關(guān)于x的偏微分可以表示為

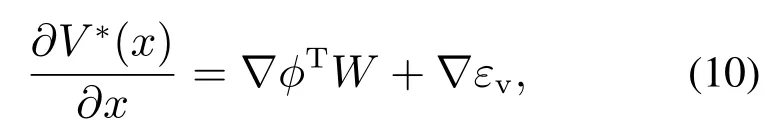
其中:W ∈Rl指逼近性能指標(biāo)后的神經(jīng)網(wǎng)絡(luò)權(quán)重,φ(x)∈Rl×n是激活函數(shù),εv為神經(jīng)網(wǎng)絡(luò)逼近誤差,l指神經(jīng)網(wǎng)絡(luò)節(jié)點(diǎn)數(shù).分別表示激活函數(shù)φ和逼近誤差εv關(guān)于x的偏微分.為了進(jìn)行穩(wěn)定性分析,給出以下關(guān)于神經(jīng)網(wǎng)絡(luò)逼近方法的假設(shè)[38].

假設(shè)1理想的神經(jīng)網(wǎng)絡(luò)權(quán)重W,激活函數(shù)φ及其偏微分?φ,逼近誤差εv及其偏微分?εv有界,即滿(mǎn)足‖W‖≤WN,‖?φ‖≤φM,‖?εv‖≤φε.

在實(shí)際應(yīng)用中選擇激活函數(shù)φ(x)為獨(dú)立基函數(shù),使用假設(shè)1和萬(wàn)能逼近定理[39],應(yīng)用式(9)–(10)能夠逼近性能指標(biāo)函數(shù)V *(x)及其偏微分,且當(dāng)l →+∞時(shí),如文獻(xiàn)[8,38]所示逼近誤差εv,?εv→0.

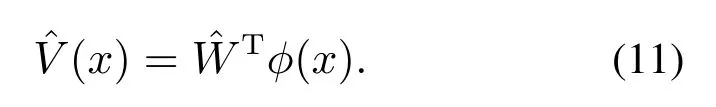
則根據(jù)式(6)–(7)和式(11),可以得到近似的H∞控制(u1,···,uN,d)為

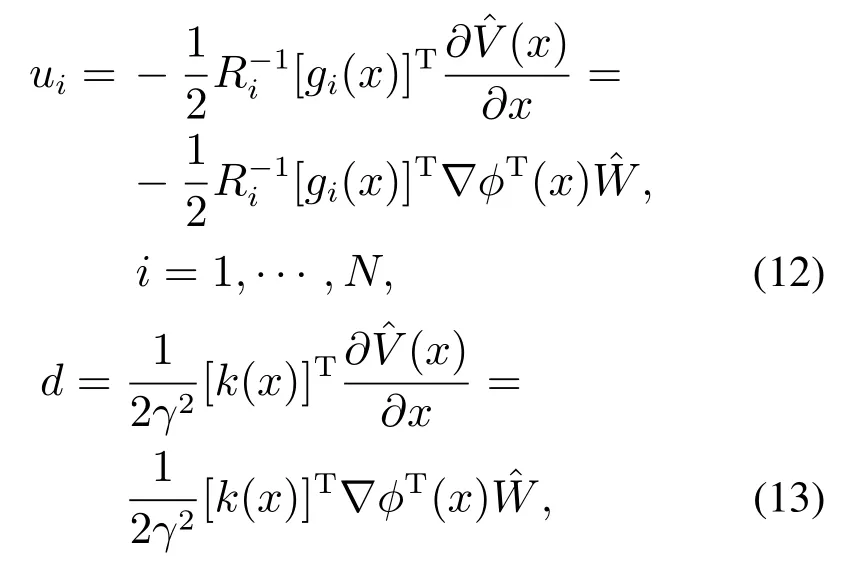
現(xiàn)有大多數(shù)H∞控制器只考慮單輸入系統(tǒng),并未考慮多輸入系統(tǒng)和給出多輸入系統(tǒng)具體的H∞控制器設(shè)計(jì)方法.雖然文獻(xiàn)[24]設(shè)計(jì)了H∞控制器,但是只考慮了線(xiàn)性系統(tǒng).本文應(yīng)用近似動(dòng)態(tài)規(guī)劃方法解決多輸入非線(xiàn)性系統(tǒng)的H∞控制器設(shè)計(jì)問(wèn)題,為多輸入受干擾系統(tǒng)的H∞控制設(shè)計(jì)提出一種新而有效的解決方案.

最后設(shè)計(jì)自適應(yīng)律更新神經(jīng)網(wǎng)絡(luò)權(quán)值?W,使其收斂于真值W附近.由于逼近的神經(jīng)網(wǎng)絡(luò)要使HJI方程趨近于零,可根據(jù)HJI方程設(shè)計(jì)權(quán)值W的自適應(yīng)律.則HJI方程可用神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)(10)重新表述為

則HJI方程(14)可以簡(jiǎn)化為

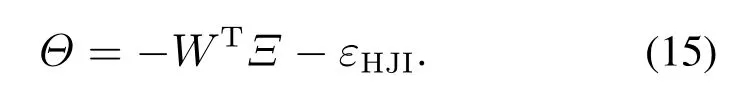
由式(15)可知,應(yīng)用簡(jiǎn)化的HJI方程將神經(jīng)網(wǎng)絡(luò)權(quán)重W表示成線(xiàn)性化的形式,因此可以用Θ和Ξ設(shè)計(jì)自適應(yīng)律更新神經(jīng)網(wǎng)絡(luò)權(quán)值,首先設(shè)計(jì)濾波輔助矩陣P ∈Rl×l和Q ∈Rl為

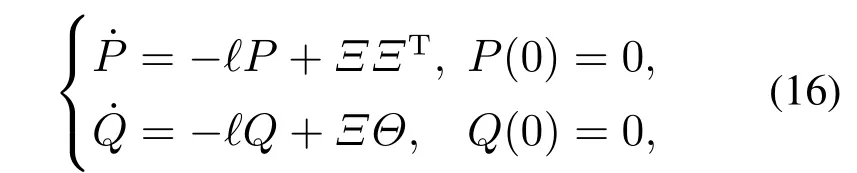
其中:?為濾波因子,P和Q分別為ΞΞ和ΞΘ的濾波矩陣.可以得到

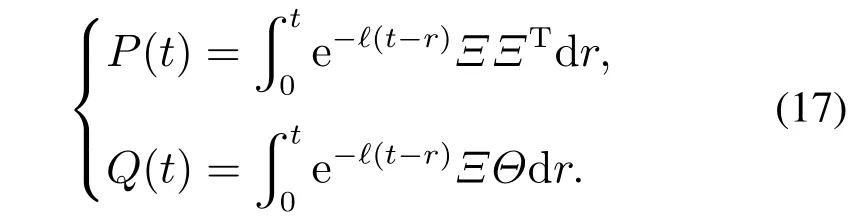
設(shè)計(jì)另一個(gè)輔助矩陣M ∈Rl為

由式(15)和式(17)可得

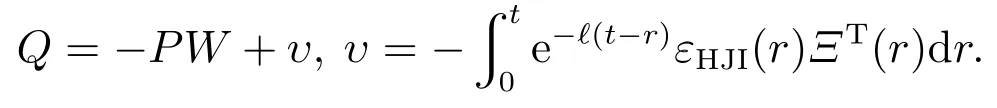
且存在正實(shí)數(shù)ευ滿(mǎn)足‖υ‖≤ευ.根據(jù)式(16)–(18)可得

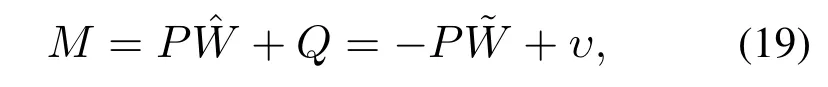
其中Γ是學(xué)習(xí)增益.

為了進(jìn)行收斂性分析,引入以下引理[15].

引理2如果式(20)中的回歸向量Ξ持續(xù)激勵(lì),則矩陣式(16)中的濾波矩P正定,即存在σ ＞0滿(mǎn)足λmin(P)＞σ ＞0.

下面給出被估神經(jīng)網(wǎng)絡(luò)權(quán)值的收斂性證明.

定理1針對(duì)逼近性能指標(biāo)的神經(jīng)網(wǎng)絡(luò)(11),應(yīng)用自適應(yīng)律(20),如果式(15)中的回歸向量Ξ持續(xù)激勵(lì),那么神經(jīng)網(wǎng)絡(luò)權(quán)值估計(jì)誤差收斂于零附近的緊集,收斂到其真值W附近.

注2文獻(xiàn)[28]應(yīng)用迭代方法解決了兩人零和博弈的最優(yōu)解,迭代值函數(shù)使其上界滿(mǎn)足＜ε,下界滿(mǎn)足＜ε,同時(shí)上下界滿(mǎn)足＜ε則停止迭代得出對(duì)應(yīng)的H∞控制對(duì).而本文直接用HJI方程的數(shù)據(jù)信息設(shè)計(jì)自適應(yīng)律,更新性能指標(biāo)神經(jīng)網(wǎng)絡(luò)權(quán)值使HJI方程趨近于零,得出最優(yōu)的值函數(shù)用于求解多輸入非線(xiàn)性系統(tǒng)的H∞控制.相比文獻(xiàn)[28]中的迭代算法,簡(jiǎn)化了程序設(shè)計(jì)步驟.

3.2 穩(wěn)定性分析

為了分析系統(tǒng)的穩(wěn)定性,將H∞控制式(12)–(13)代入系統(tǒng)(1)可以得到

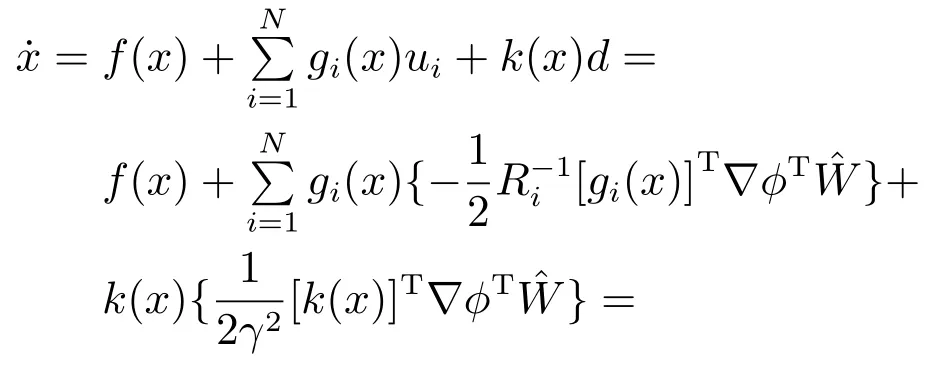
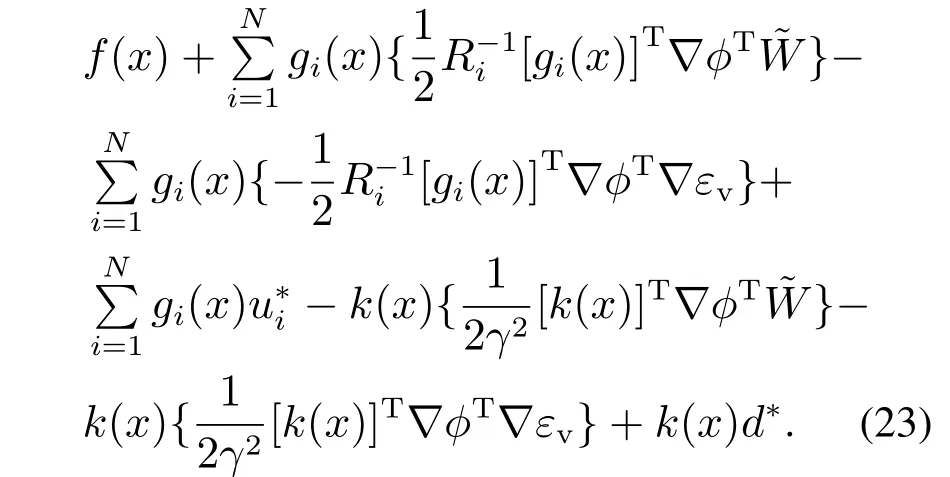
給出以下關(guān)于系統(tǒng)動(dòng)態(tài)有界的假設(shè)[40–41].

假設(shè)2[40–41]非線(xiàn)性多輸入系統(tǒng)(1)中各動(dòng)態(tài)滿(mǎn)足‖f(x)‖≤bf‖x‖,‖gi(x)‖≤bgi,‖k(x)‖≤bk,其中bf＞0,bg＞0,bk ＞0.

總結(jié)全文可以得出以下定理.

定理2針對(duì)多輸入帶干擾的非線(xiàn)性系統(tǒng)(1),使用H∞控制式(12)–(13),權(quán)值自適應(yīng)律(20),如果回歸向量φ和Ξ持續(xù)激勵(lì),則神經(jīng)網(wǎng)絡(luò)權(quán)值估計(jì)誤差～W一致最終有界,式(12)中的H∞控制ui收斂到式(6)中的真值附近,式(13)中的最壞干擾d收斂到式(7)中的真值d*附近,即存在正實(shí)數(shù)?ui,?d滿(mǎn)足‖ui-≤?ui,‖d-d*‖≤?d.

證考慮以下李雅普諾夫函數(shù)

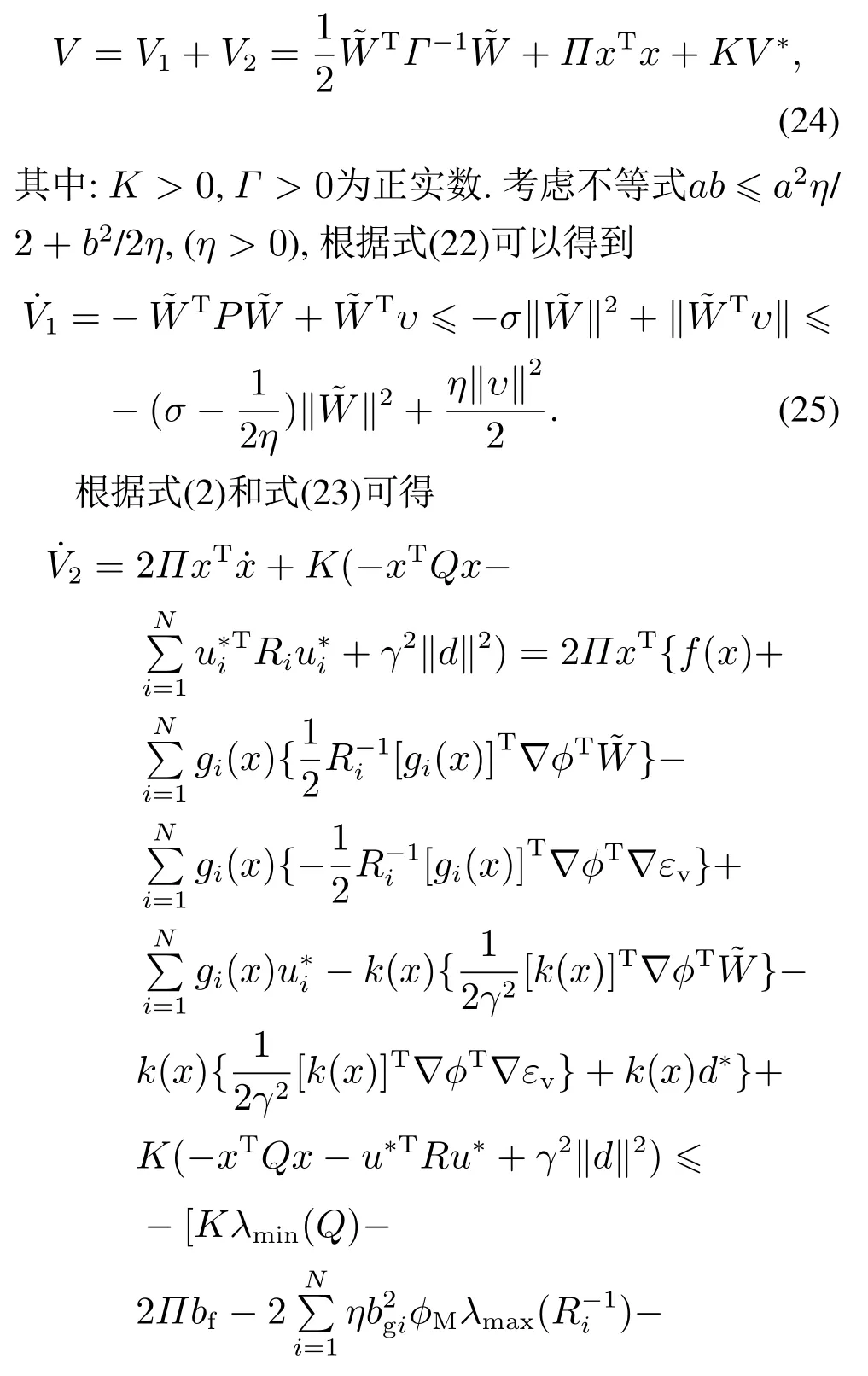
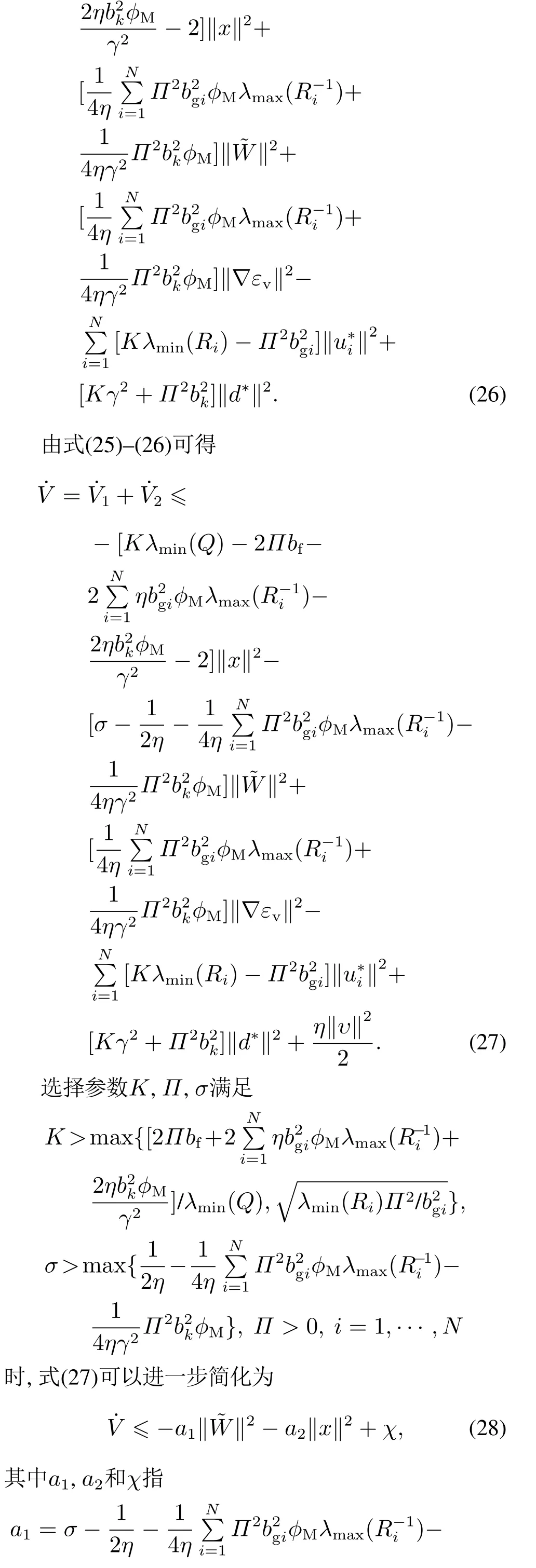
最后可以得到最優(yōu)H∞控制和近似值之間的誤差為

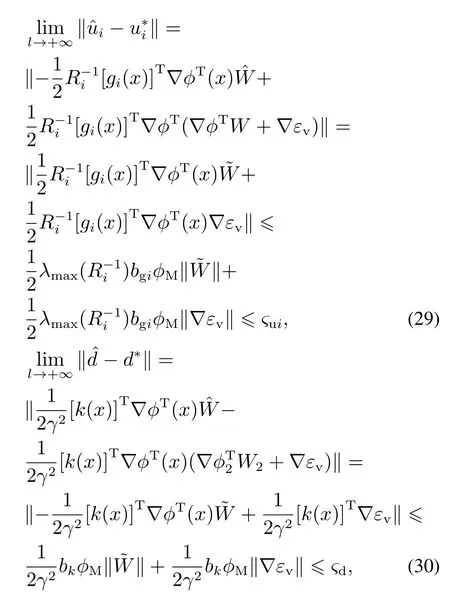
其中:?ui ＞0,?d＞0是由神經(jīng)網(wǎng)絡(luò)逼近誤差和權(quán)值估計(jì)誤差導(dǎo)致的誤差因子,當(dāng)神經(jīng)網(wǎng)絡(luò)節(jié)點(diǎn)l →∞,誤差因子將收斂到零,非線(xiàn)性多輸入系統(tǒng)的近似H∞控制收斂到最優(yōu)值. 證畢.

4 仿真驗(yàn)證

考慮以下非線(xiàn)性系統(tǒng)[36]

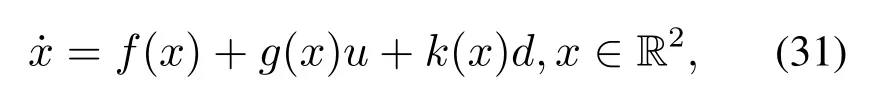
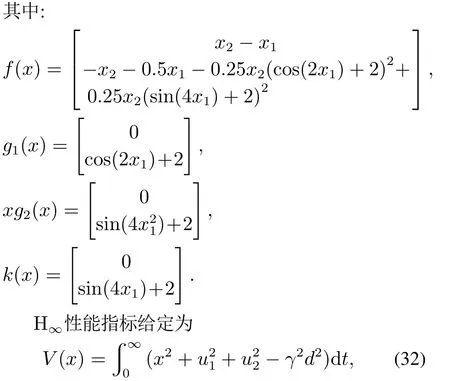
其中γ=8為衰減因子.

仿真中,設(shè)置系統(tǒng)初值為[4-4]T,應(yīng)用性能指標(biāo)函數(shù)的逼近神經(jīng)網(wǎng)絡(luò)(11),激活函數(shù)設(shè)置為φ(x)=,使用權(quán)值自適應(yīng)律(20),自適應(yīng)律中各參數(shù)設(shè)置為=0,Q=diag{[1 1]},R1=R2=1,?=1,Γ=diag{[30 30 30]}.圖1為神經(jīng)網(wǎng)絡(luò)權(quán)值?W的收斂效果,根據(jù)式(12)–(13),可得圖2的H∞控制,圖3為系統(tǒng)狀態(tài).可以看出,應(yīng)用所設(shè)計(jì)的H∞控制能夠使多輸入系統(tǒng)性能指標(biāo)收斂,且系統(tǒng)穩(wěn)定.

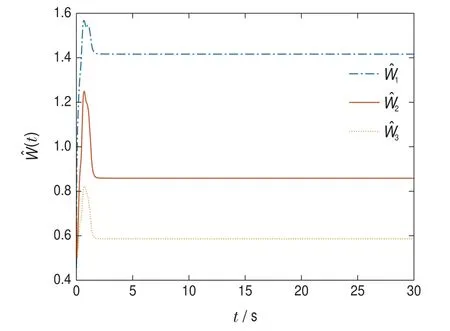
圖1 近似神經(jīng)網(wǎng)絡(luò)權(quán)重Fig.1 Approximate NN weights

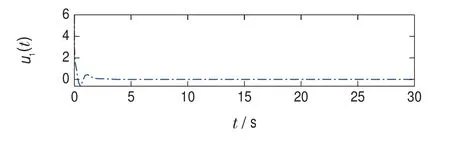
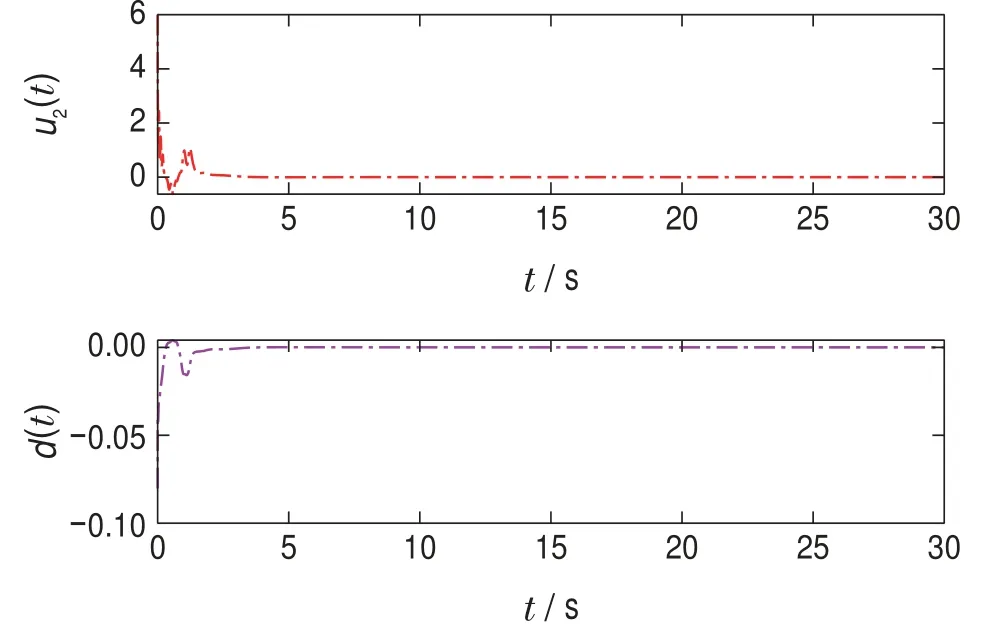
圖2 H∞控制u1,u2和最壞干擾dFig.2 H∞controls u1,u2 and d

圖3 系統(tǒng)狀態(tài)Fig.3 System states

為了驗(yàn)證本文所設(shè)計(jì)H∞控制器的有效性,在仿真時(shí)間為t=15 s時(shí),加入一個(gè)常值d=0.1 s的外部干擾.H∞控制的變化結(jié)果和系統(tǒng)狀態(tài)如圖4所示;另外在t=15 s時(shí)加入另一個(gè)有界時(shí)變擾動(dòng)d=0.1 sint,H∞控制的運(yùn)行結(jié)果和系統(tǒng)狀態(tài)如圖5所示.

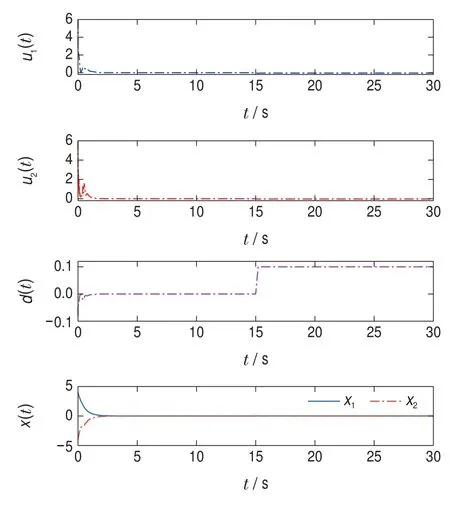
圖4 d=0.1下的H∞控制和系統(tǒng)狀態(tài)Fig.4 H∞controls and system states with d=0.1

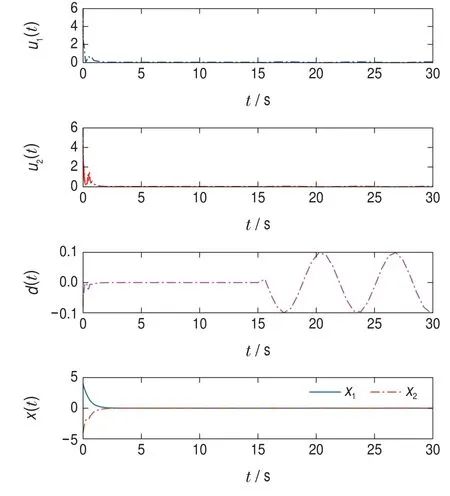
圖5 d=0.1 sin t下的H∞控制和系統(tǒng)狀態(tài)Fig.5 H∞controls and system states with d=0.1 sin t

可以看出,在多輸入系統(tǒng)H∞控制求解出來(lái)以后,系統(tǒng)再收到其他外部常值或者有界時(shí)變干擾,能夠以更加滿(mǎn)足H∞性能指標(biāo)的形式穩(wěn)定運(yùn)行.

5 結(jié)論

針對(duì)多輸入帶干擾的非線(xiàn)性系統(tǒng),提出應(yīng)用近似動(dòng)態(tài)規(guī)劃方法解決其H∞控制.首先給出多輸入系統(tǒng)H∞控制問(wèn)題的描述,定義納什均衡解.由于非線(xiàn)性的HJI方程難以求解,應(yīng)用神經(jīng)網(wǎng)絡(luò)逼近最優(yōu)解,引進(jìn)一種新的自適應(yīng)律更新神經(jīng)網(wǎng)絡(luò)權(quán)值,直接用于H∞控制器的設(shè)計(jì).對(duì)權(quán)值的收斂性和在所設(shè)計(jì)H∞控制作用下的系統(tǒng)穩(wěn)定性進(jìn)行分析和證明.最后用一個(gè)非線(xiàn)性多輸入仿例證明所提出方法的正確性和有效性.未來(lái)工作筆者會(huì)將這種H∞控制方法應(yīng)用于非晶薄帶的制造過(guò)程.