黃鋮

(華中科技大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 湖北 武漢 430000)

1.引言

對(duì)于半直線上Strum-Liouville方程-u′′(x)-P(x)u′(x)+Q(x)u(x) =k2u(x), 邊界條件為：u(k,0)=0,u′(k,0)=1,P(x)與Q(x)為未知函數(shù)且P(x)大于0, 本文先給出了單個(gè)方程轉(zhuǎn)化為方程組形式, 并結(jié)合矩陣薛定諤算子理論給出方程有兩個(gè)未知量的重建公式.

經(jīng)典Strum-Liouville問題的一般形式為：

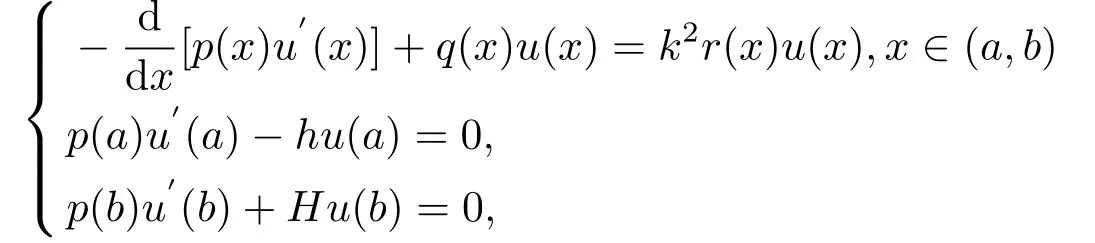
這里系數(shù)p(x), 勢(shì)函數(shù)q(x)和權(quán)函數(shù)r(x)都是區(qū)間[a,b]上的實(shí)值函數(shù).

邊界條件中h=∞和H=∞分別表示u(a)=0,u(b)=0,稱為在端點(diǎn)a和b處滿足狄利克雷邊界條件;h=0和H=0時(shí)的邊條件u′(a)=0,u′(b)=0,稱為Neumann邊界條件.

Strum-Liouville問題起始于19世紀(jì)最初探究固體熱傳導(dǎo)問題的傅里葉方法, 隨著泛函分析中的無界算子理論發(fā)展, Strum-Liouville算子理論成為現(xiàn)代數(shù)學(xué)物理研究的一個(gè)重要分支.

關(guān)于薛定諤算子逆散射問題的研究, 奠基性的工作是由Marchenko和Faddeev[1]給出的, 他們分別給出了半直線上和全直線上逆散射問題解的存在性和唯一性.特別地, 他們證明了散射數(shù)據(jù)與一類勢(shì)函數(shù)一一對(duì)應(yīng)的充分必要條件.這里的散射數(shù)據(jù)由束縛態(tài)數(shù)據(jù)(有限個(gè)特征值與對(duì)應(yīng)的規(guī)范化常數(shù))和反射系數(shù)構(gòu)成.Deift[2]給出一維全直線上通過反射系數(shù)重建單個(gè)位勢(shì)結(jié)果.我們將重建關(guān)于位勢(shì)的兩個(gè)未知量.Rundell與Sacks利用有限區(qū)間的薛定諤算子逆譜問題的數(shù)值算法給出逆共振的數(shù)值算法[3].

矩陣薛定諤算子是量子力學(xué)中的一類微分算子, 應(yīng)用在量子散射, 圖散射等領(lǐng)域, 這類研究最早Marchenko考慮的是半直線具有狄利克雷邊界條件的逆問題.由于一般自伴比狄利克雷條件應(yīng)用廣泛, 故可以直接考慮矩陣邊界條件為自伴矩陣薛定諤算子[4].

2.半直線上Strum-Liouville位勢(shì)重構(gòu)

首先考慮矩陣薛定諤方程, 形式為：

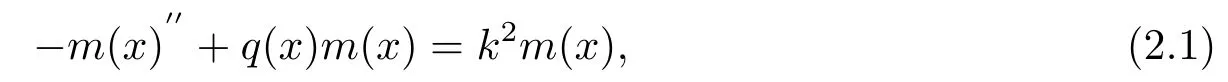
方程中m(x)為n維列向量,q(x)為n×n階Hermite矩陣, 令I(lǐng)n為n×n單位矩陣.(2.1)式展開形式為

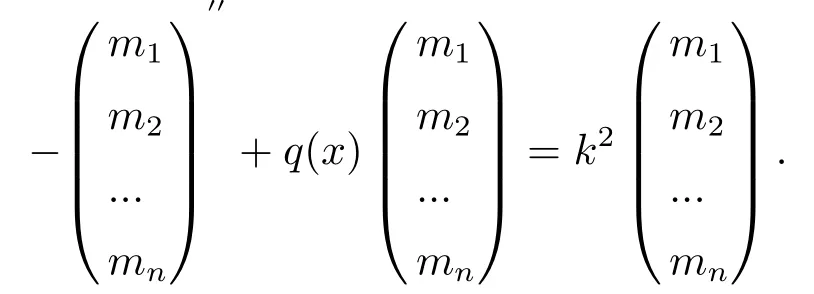
設(shè)f(x,k)為矩陣薛定諤方程(2.1)滿足下列漸進(jìn)性的Jost解[5]：

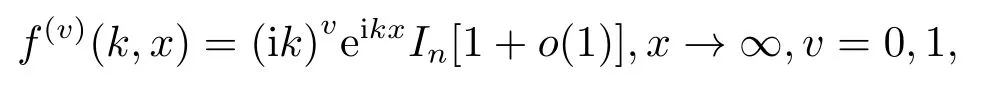
進(jìn)一步

Jost解f(x,k)具有如下性質(zhì)[5]：

1) 對(duì)于每一個(gè)固定的x ∈R,f(x,k)關(guān)于k在上半復(fù)平面上解析, 且連續(xù)到實(shí)軸?.進(jìn)一步,f(x,k)對(duì)k關(guān)于x ≥0一致滿足漸進(jìn)性：

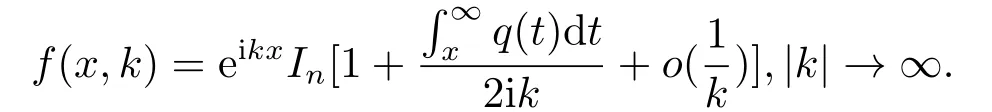
2) Jost解f(x,k)有積分算子表示

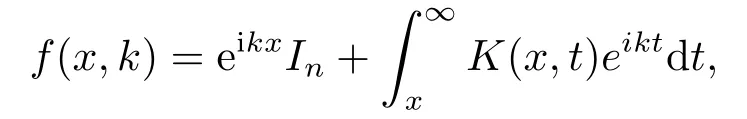
其中積分核K(x,t)關(guān)于x和t都具有一階偏導(dǎo)數(shù), 且滿足

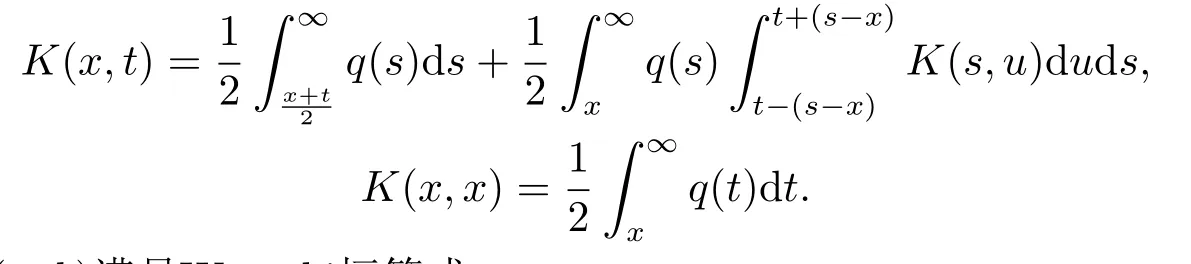
3) Jost解f(x,k)滿足Wronski恒等式

[f(x,-k),f(x,k)]=2ik.

本文所研究的Strum-Liouville重構(gòu)問題中, 上述的n取2, 且位勢(shì)變?yōu)閷?shí)值的滿足條件限制:

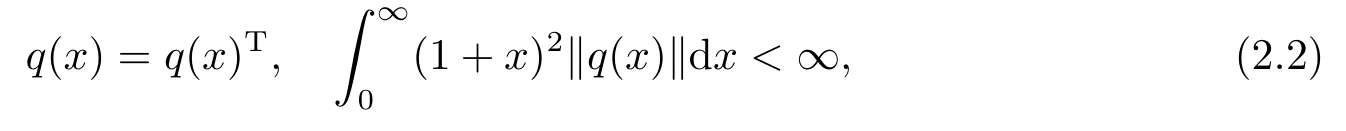
這里矩陣范數(shù)定義為：

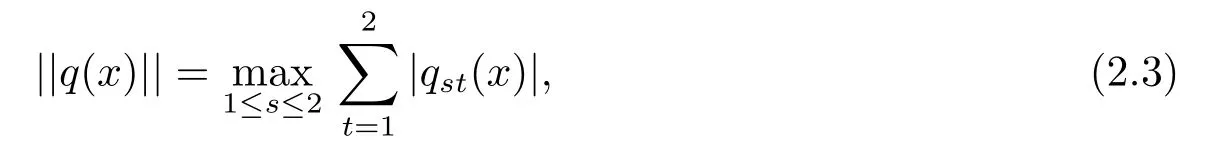
qst(x)表示矩陣q(x)的第s行第t列元素, 展開即為：

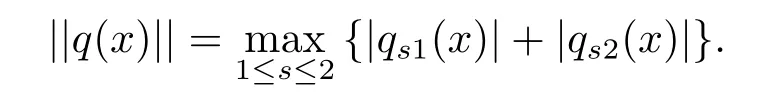
對(duì)于矩陣薛定諤方程, 其中的Jost矩陣與散射矩陣S(k)是我們重點(diǎn)要觀察的內(nèi)容.

定義2.1定義Jost矩陣[5]

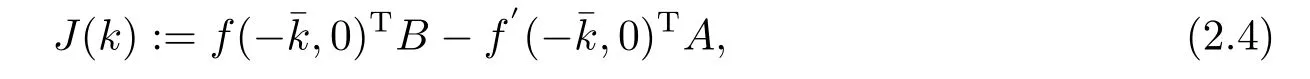
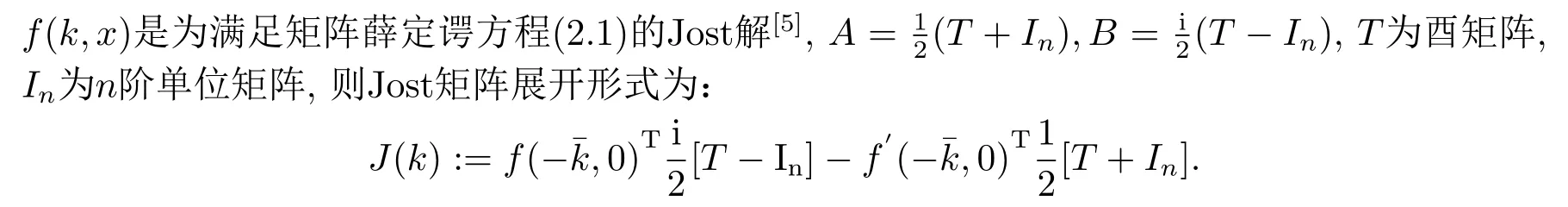
對(duì)于Jost矩陣有下列性質(zhì)[5].

命題2.2設(shè)矩陣勢(shì)函數(shù)q(x)滿足, 則Jost矩陣有以下結(jié)論[5]：

1) Jost矩陣J(k)在k ∈R{0}上可逆, 且可能有detJ(0)=0;

2) Jost矩陣的行列式detJ(k)在有至多有限個(gè)零點(diǎn), 并且都分布在正半虛軸iR+上;

3) 若detJ(k)=0, 則k為J(k)-1的簡單極點(diǎn)即：

其中N-,κN0,κ為常矩陣, 且N-,κ0n.

定義2.3在矩陣薛定諤方程中我們定義散射矩陣[5]

散射矩陣有如下性質(zhì).

命題2.4設(shè)矩陣勢(shì)函數(shù)q(x)滿足(2.2), 則散射矩陣S(k)在R上連續(xù), 且滿足：

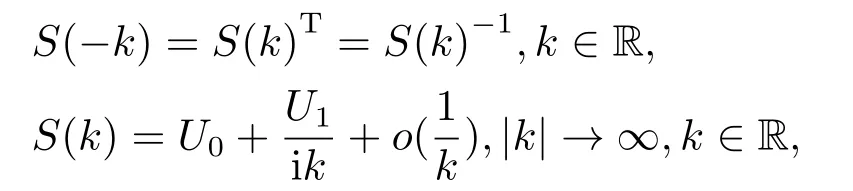
其中U1為Hermite矩陣,U0為酉Hermite矩陣.

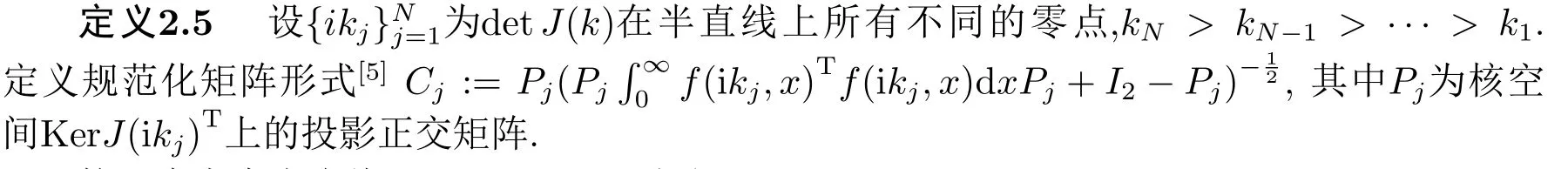
接下來考慮半直線Strum-Liouville方程

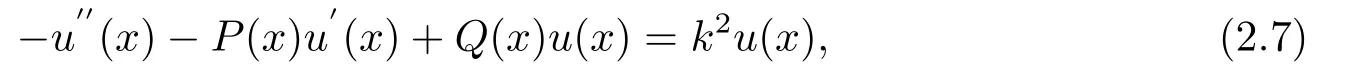
邊界條件為u(k,0) = 0,u′(k,0) = 1, 記Strum-Liouville方程的散射矩陣為s(k), 下面給出重構(gòu)結(jié)論.

定理2.6方程-u′′(x)-P(x)u′(x)+Q(x)u(x)=k2u(x),u(k,0)=0,u′(k,0)=1為方程邊界條件, 在半直線上當(dāng)P(x)＞0, 位勢(shì)Q(x)滿足||Q(x)|| ≤ce-xγ,c ＞0,γ ＞1時(shí),可通過原方程的散射數(shù)據(jù)s(k)來重構(gòu)出位勢(shì)Q(x)與P(x).

證首先把Strum-Liouville算子方程

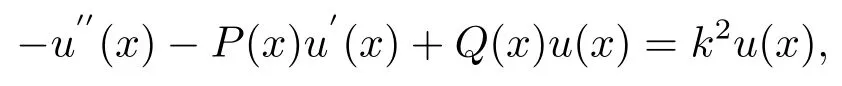
Strum-Liouville算子方程轉(zhuǎn)化后打開的形式為：

可見(2.8)與(2.9)兩個(gè)方程關(guān)系密切.

(2.8)打開后方程為:

(2.9)打開后方程為：

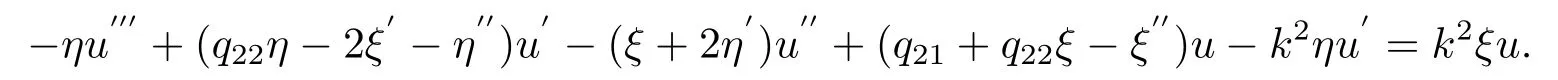
把(2.8)(2.9)每個(gè)方程中各項(xiàng)指標(biāo)進(jìn)行一一對(duì)應(yīng)可以得出：

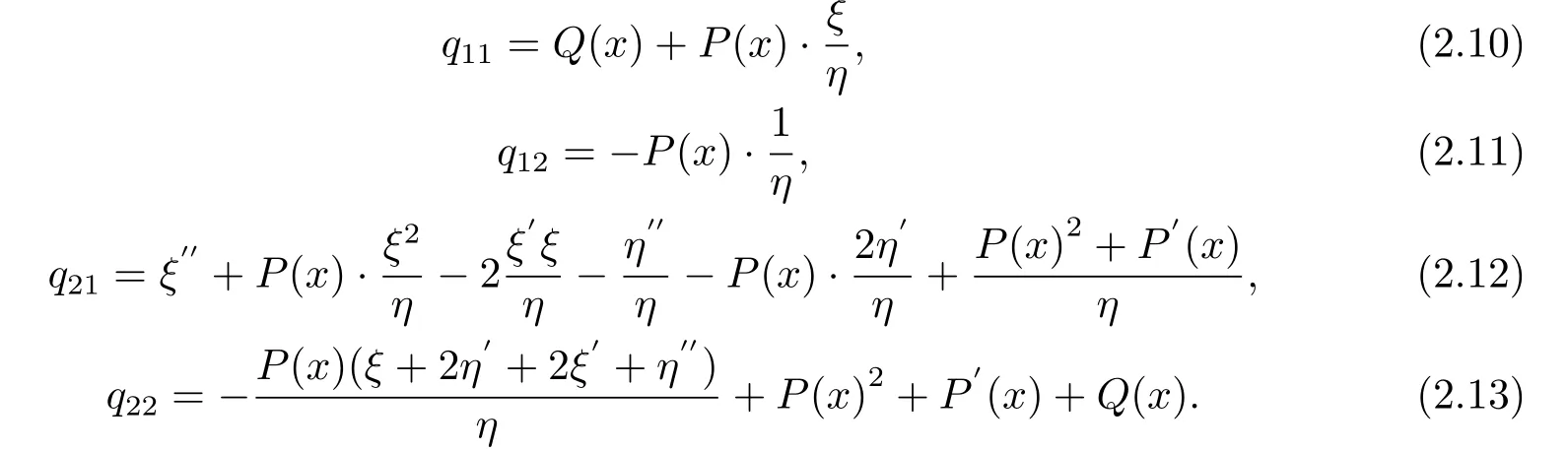
根據(jù)q(x)=q(x)T得q12=q21,該等式可得到ξ所滿足的方程：

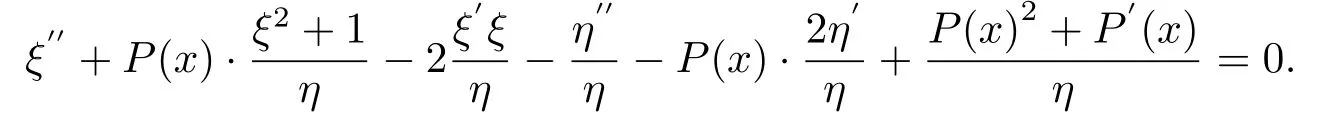
由于一個(gè)方程轉(zhuǎn)化成方程組, 且方程組中的這兩個(gè)方程之間有聯(lián)系, 計(jì)算時(shí)會(huì)多出有一個(gè)條件限制即：

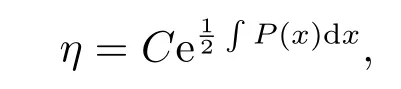
這樣就完成了方程轉(zhuǎn)化后的方程組新形式, 接下來是對(duì)方程組的性質(zhì)展開研究.

對(duì)于邊界條件的轉(zhuǎn)化, 最初考慮的是邊界條件為

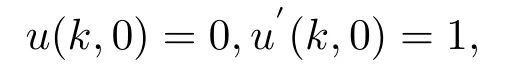
轉(zhuǎn)化為方程組后對(duì)矩陣薛定諤算子可直接考慮半直線上具有一般自伴邊界條件的矩陣薛定諤算子,

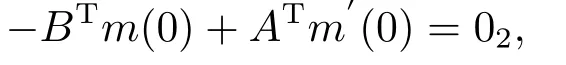
綜上Strum-Liouville算子方程-u′′(x)-P(x)u′(x)+Q(x)u(x)=k2u(x), 已變?yōu)榫仃囇Χㄖ@算子-m′′+qm=k2m形式, 邊界條件變?yōu)榫哂幸话阕园檫吔鐥l件：

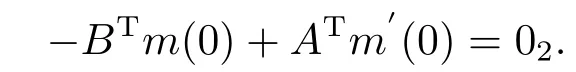
未知位勢(shì)考慮具有衰減條件||q(x)|| ≤ce-xγ,c ＞0,γ ＞1, 下面探究Strum-Liouville算子方程散射矩陣s(k)與矩陣薛定諤算子散射矩陣S(k)關(guān)系.

薛定諤方程形式為：

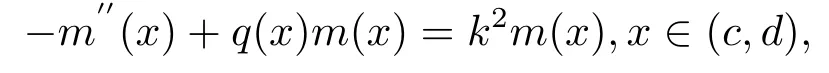
(c,d)=(-∞,+∞), 位勢(shì)這里

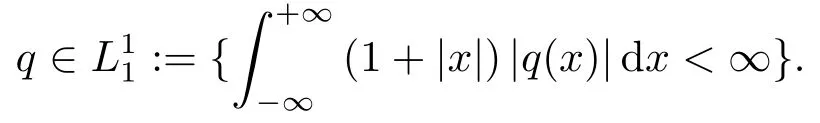
m1(x,k),m2(x,k)為Hmj=k2mj,j= 1,2,的解,H為帶實(shí)位勢(shì)自伴薛定諤算子.解有著如下性質(zhì)：

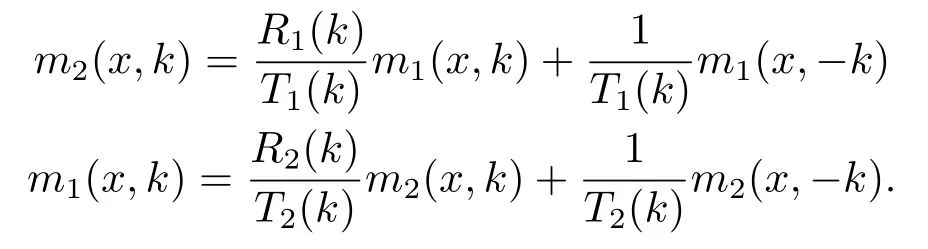
T(k)為傳輸系數(shù),R(k)為反射系數(shù),T2(k)m1(x,k)表示的是e-ikx平面波從-∞向正向傳播,T2(k)eikx向+∞同時(shí)R2(k)e-ikx往-∞.反射, 同理,T1(k)m2(x,k)表示的是波從+∞向-∞傳播,表達(dá)形式具有物理意義.

此時(shí)所形成的位勢(shì)的散射矩陣為：

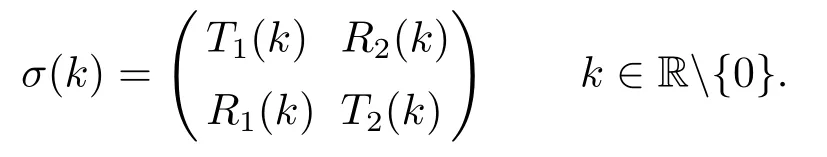
Strum-Liouville算子方程(2.7)的散射矩陣記為s(k), 設(shè)u1(x,k),u2(x,k)為方程的兩個(gè)線性無關(guān)解, 對(duì)于Strum-Liouville算子方程我們?nèi)≡摼€性無關(guān)解作列向量依舊可以形成上述形式的二階散射矩陣.矩陣薛定諤方程散射矩陣記為S(k), 根據(jù)定義S(k) =-J(-k)J(k)-1,由(2.4)得散射矩陣展開后是和Jost解相關(guān).

最后給出重構(gòu)q(x)過程：

1) 通過觀察S(k)在虛軸iR+上的值找到所有特征值.

當(dāng)detJ(k)=0時(shí),則k為J(k)-1的簡單極點(diǎn).結(jié)合定義S(k)=-J(-k)J(k)-1,當(dāng)J(-kj)=0n, 說明S(k)有簡單極點(diǎn), 并通過解析延拓可唯一確定, 通過k在軸上運(yùn)動(dòng), 觀察散射矩陣S(k)找到所有的k1,··· ,kN-1,kN.

2) 利用散射矩陣和特征值可得所有的的規(guī)范化矩陣.

首先根據(jù)文[4]可得Cj0, 且

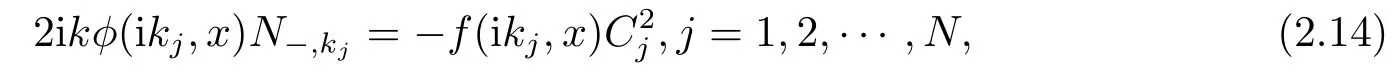
根據(jù)(2.4),(2.5),(2.6)得

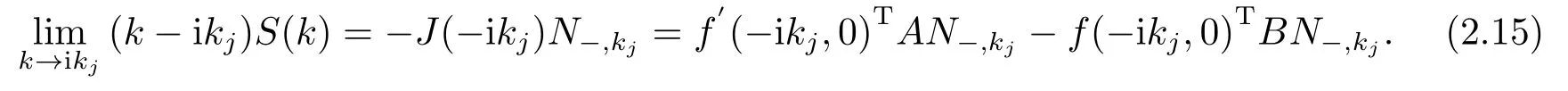
設(shè)φ(k,x)為矩陣薛定諤方程滿足下列初始條件的解：

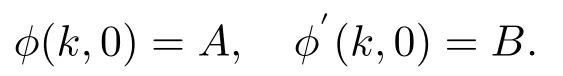
由φ的初始條件得：

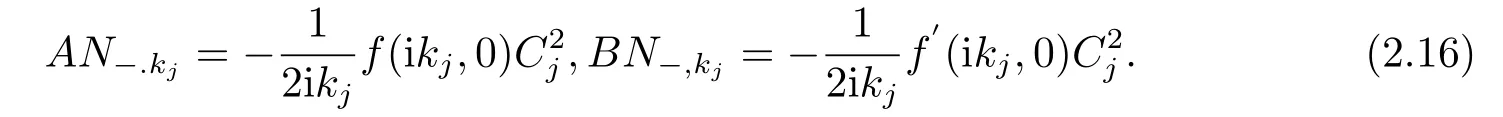
將上式代入(2.15)中得：

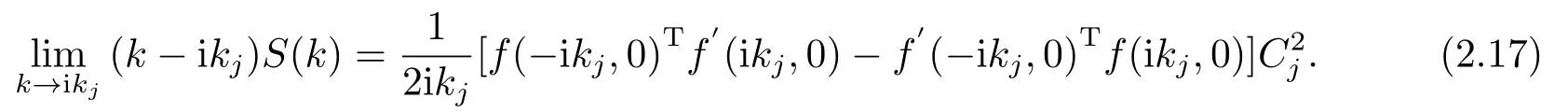
利用漸進(jìn)估計(jì)

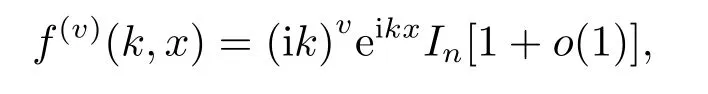
令k=±ikj, 得

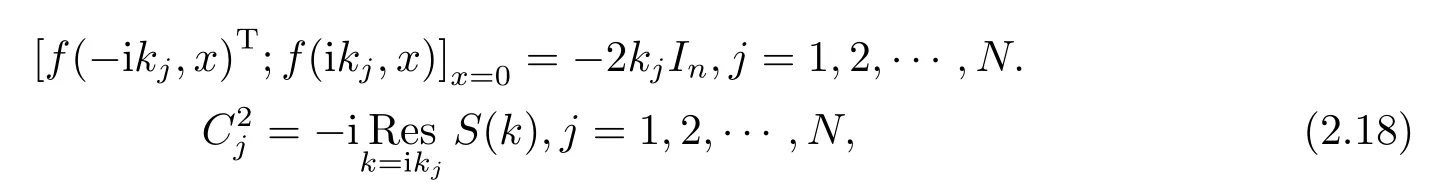
所以通過散射矩陣是可以確定出規(guī)范化矩陣.

3) 利用Marchenko程序重構(gòu)q(x).

已知Marchenko方程：

其中F(x):=

根據(jù)第二步我們會(huì)得出規(guī)范化矩陣結(jié)果, 通過F(x)的表達(dá)式

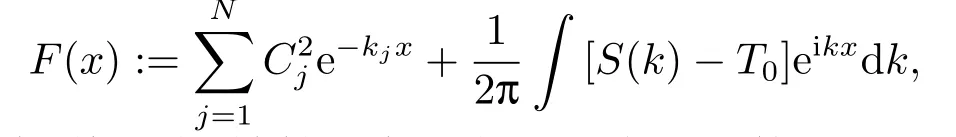
得知F(x)與規(guī)范化矩陣, 特征值, 散射矩陣相關(guān), 進(jìn)而代入可算出F(x), 由于位勢(shì)公式表達(dá)式與積分核相關(guān)：

尋找q(x)與Q(x)的關(guān)系,根據(jù)(2.10),(2.13)由于q(x)的指標(biāo)里包含Q(x),只需要根據(jù)q11或q22的重構(gòu)出的表達(dá)式, 這樣Q(x)就被表示出來.

3.總結(jié)

本文研究的是半直線上Strum-Liouville方程逆散射問題, 給出在半直線上重建位勢(shì)的方法, 結(jié)合矩陣薛定諤的算子理論, 把Strum-Liouville方程轉(zhuǎn)化為方程組, 討論方程組逆散射性質(zhì)及轉(zhuǎn)化后的方程組與原方程之間的聯(lián)系, 對(duì)Strum-Liouville方程給出可利用散射矩陣, 特征值及規(guī)范化矩陣重構(gòu)位勢(shì)的結(jié)論.文章中對(duì)位勢(shì)提出的超指數(shù)衰減條件||Q(x)|| ≤ce-xγ,c ＞0,γ ＞1, 目的為了保證Jost解f(x,k)關(guān)于k可解析延拓, 該條件可以放寬到指數(shù)衰減.