王亞男, 滕凱民

(太原理工大學(xué)數(shù)學(xué)學(xué)院, 山西晉中 030600)

1.引言

本文考慮如下p-Laplace型擬線性薛定諤方程正解的存在性

當(dāng)κ < 0時(shí), 在文[4]中, Poppenberge等人通過(guò)約束極小化方法, 考慮了方程(1.3)正解的存在性.之后, LIU等人[5]通過(guò)變量代換將擬線性問(wèn)題轉(zhuǎn)化為半線性問(wèn)題, 并以O(shè)rlicz-Sobolev空間框架作為工作空間,利用山路定理證明了方程(1.3)正解的存在性.同時(shí)Colin和Jeanjean[6]采用對(duì)偶方法, 選取Sobolev空間H1(RN)作為工作空間, 利用山路定理研究了方程(1.3)正解的存在性.LIU等人在文[7]中引入新的擾動(dòng)方法, 研究了一類次臨界擬線性問(wèn)題, 并在文[8]中證明了臨界情況下解的存在性.此外, 利用Nehari流形, LIU等人在文[9]中研究了基態(tài)解的存在性.

當(dāng)κ>0時(shí), Alves等人在文[10]中考慮了非線性項(xiàng)

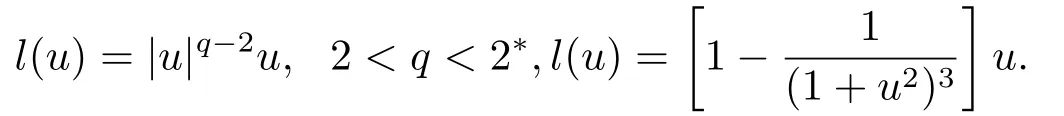
其中V 和Q在原點(diǎn)處可以是奇異的, 無(wú)界的, 或在無(wú)窮遠(yuǎn)處消失的位勢(shì), 他們利用極大極小方法和L∞估計(jì), 證明了該方程非負(fù)解和非零解的存在性.在文[16]中, Aires和Souto同樣使用了文[10]中的變量代換, 研究了方程(1.3)非線性項(xiàng)是超線性情形.

然而, 對(duì)于消失位勢(shì)的p-Laplace型擬線性薛定諤方程, 關(guān)于其正解的存在性研究的結(jié)果不多.本文的主要目的是, 利用山路定理研究方程(1.1)當(dāng)κ > 0和位勢(shì)V(x)在無(wú)窮遠(yuǎn)處消失時(shí),其正解的存在性.

為了陳述主要結(jié)果, 我們假設(shè)V(x):RN→R滿足如下條件:

2.準(zhǔn)備工作

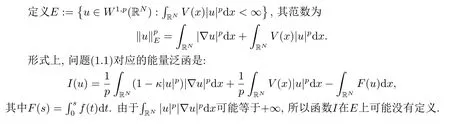
另一方面, 由于位勢(shì)V(x)可能是局部的, 我們采用罰函數(shù)方法考慮如下輔助問(wèn)題

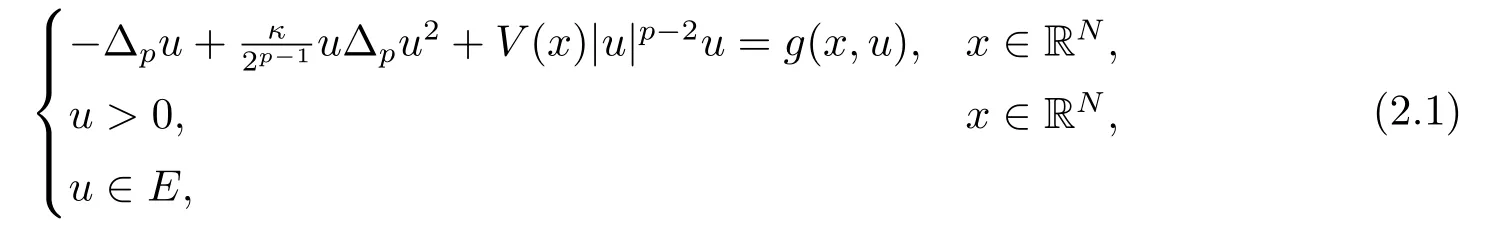
其相對(duì)應(yīng)的形式能量泛函為:

證根據(jù)l的定義, 有

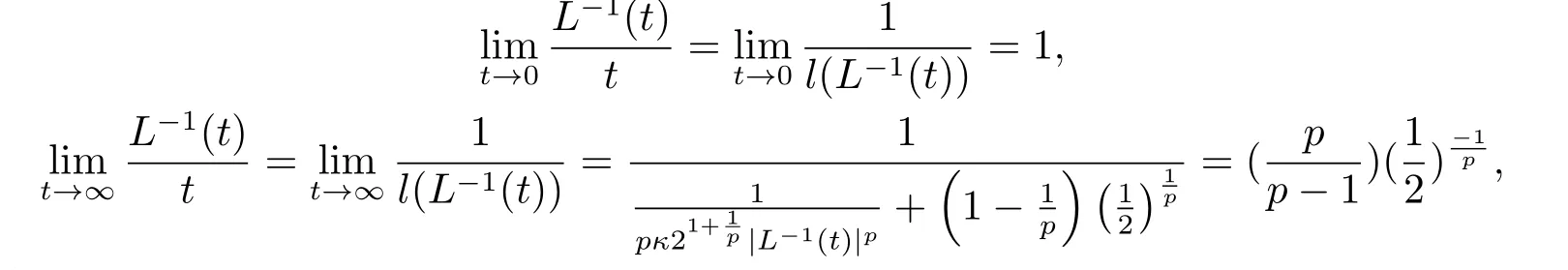
這就得到了(i)和(ii).

3.正解的存在性證明

J滿足山路幾何結(jié)構(gòu).

引理3.1假設(shè)(V1), (f1)-(f4)成立, 那么

(i)存在ρ,α>0, 使得J(v)≥α, 且∥v∥E=ρ;

(ii)存在e ∈E, 使得∥e∥E>ρ和J(e)<0.

證(i) 由引理2.2的(iii)和引理2.3的1)可得

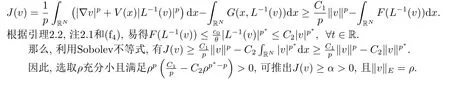
(ii) 根據(jù)(f4), 存在正常數(shù)C1,C2使得

根據(jù)引理2.2的(iv), 有

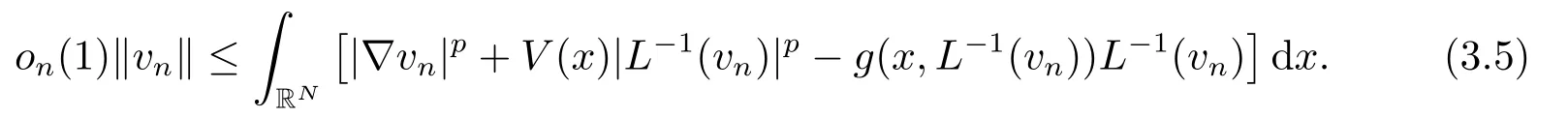
結(jié)合(3.2)和(3.5)式, 可推導(dǎo)出

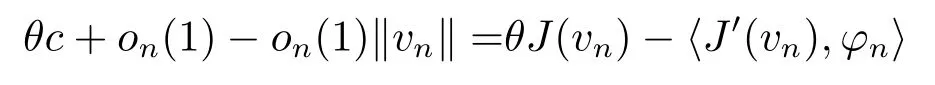
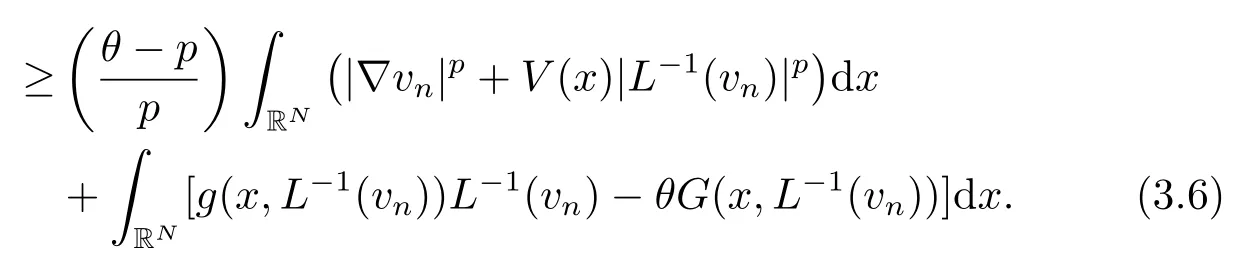
根據(jù)引理2.3的5)可得

因此v?= 0 a.e.在RN, 且v ≥0.由強(qiáng)極大值原理, 即知v > 0在RN.由此可得u = L?1(v)是方程(1.1)的正解.

引理3.4當(dāng)R>1時(shí), v ∈E是如下方程的一個(gè)弱解

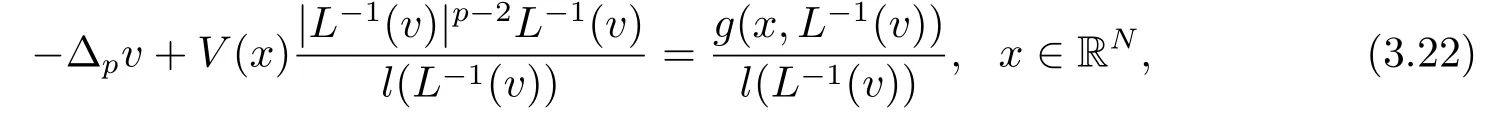
證由v是J的臨界點(diǎn), 可得

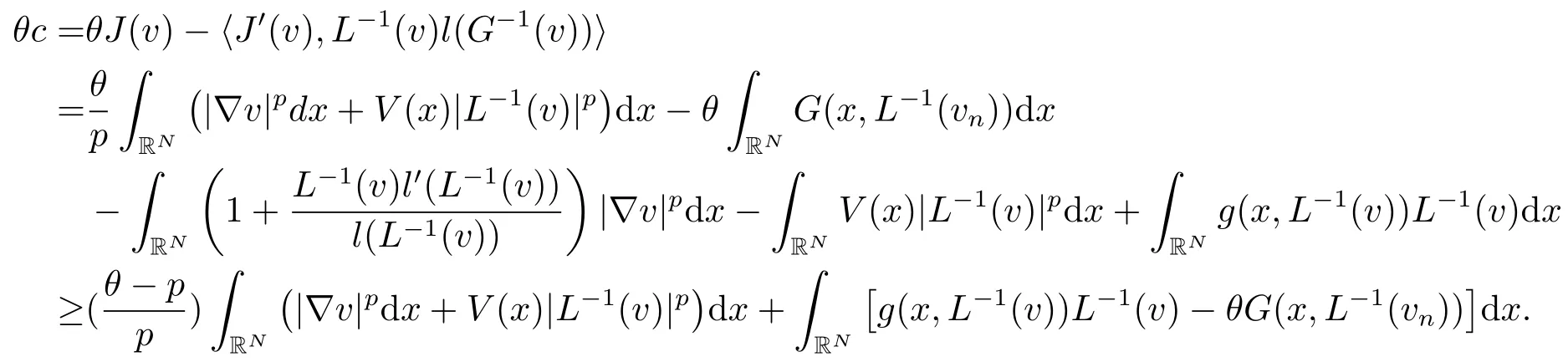
利用引理2.3的5), 有

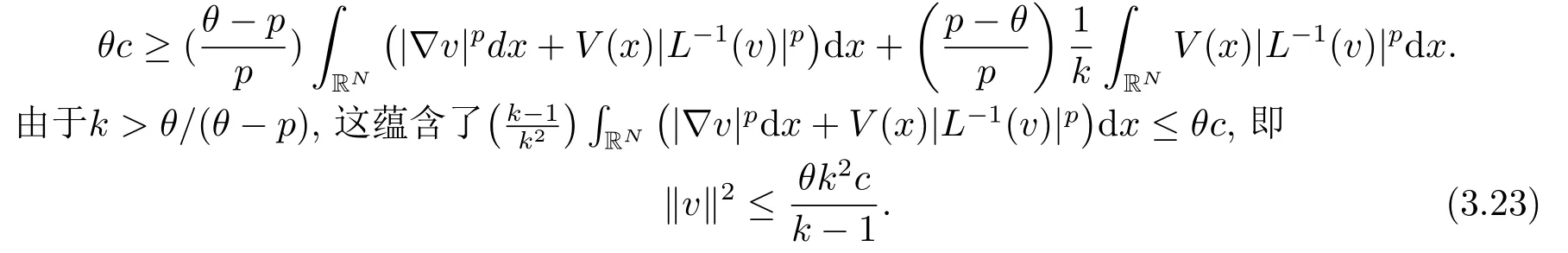
引理3.5存在M >0滿足∥v∥∞≤M∥v∥p?.

證對(duì)任意的m ∈N, β >1, 令A(yù)m={x ∈RN;|v|β?1≤m}, Bm=RNAm和

注意到vm∈E.通過(guò)計(jì)算?vm, 可得

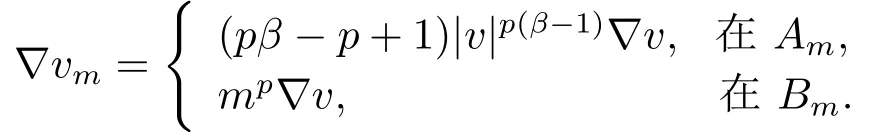
因此, 取vm為測(cè)試函數(shù), 有

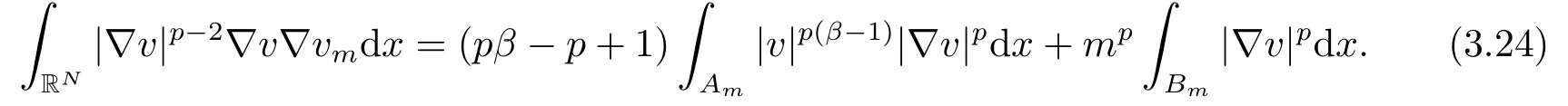
現(xiàn)在, 令

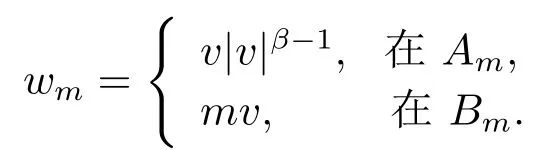
這蘊(yùn)含了|wm|p=|v|p?1vm≤|v|pβ和

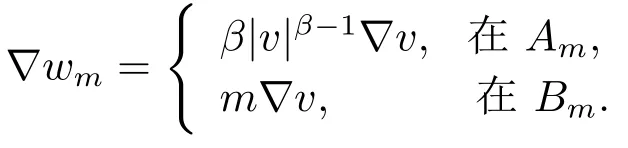
事實(shí)上

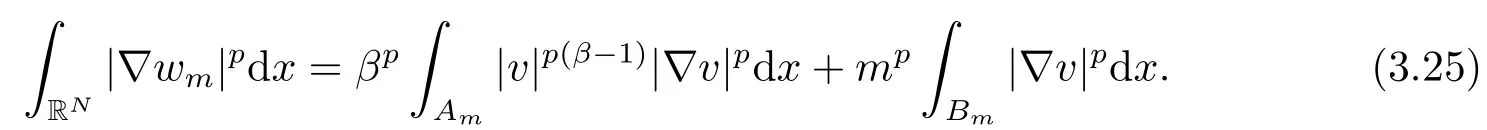
那么, 結(jié)合(3.24)和(3.25)式, 有

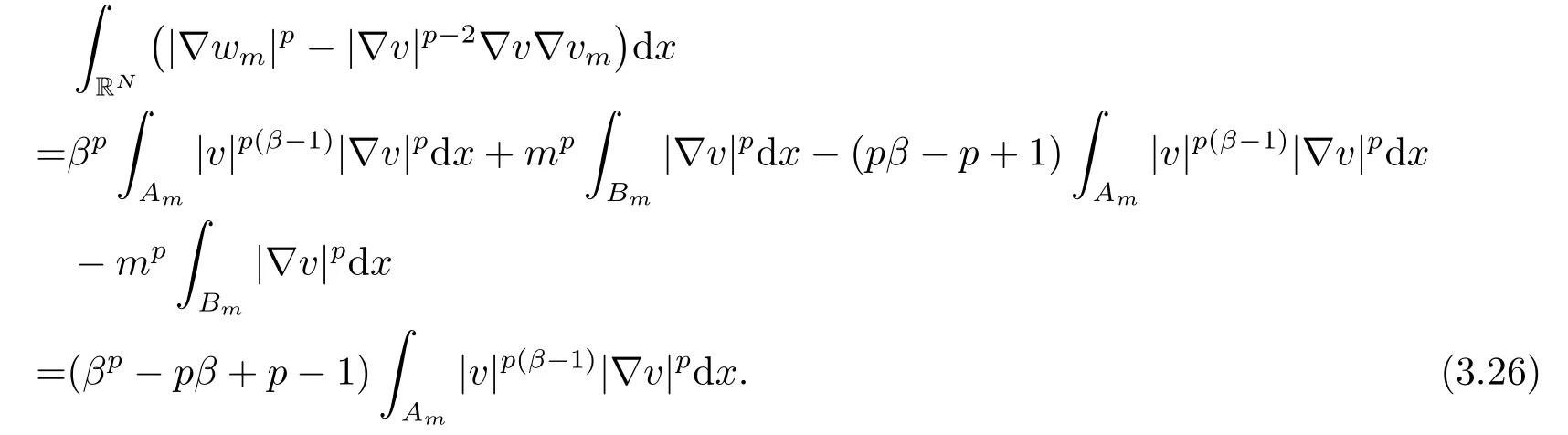
利用vm為測(cè)試函數(shù), 可推出

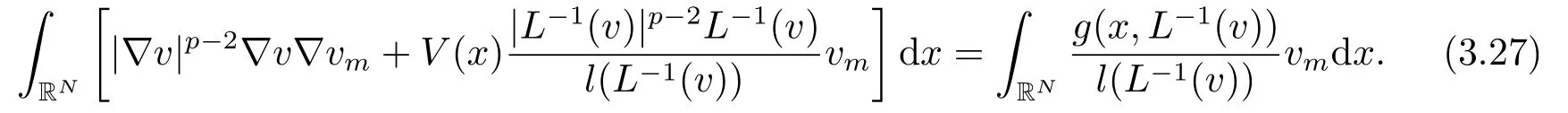
結(jié)合(3.24), (3.26)和(3.27)式, 易得

事實(shí)上, 當(dāng)|x|=R時(shí), v(x)≤u(x).選取測(cè)試函數(shù)

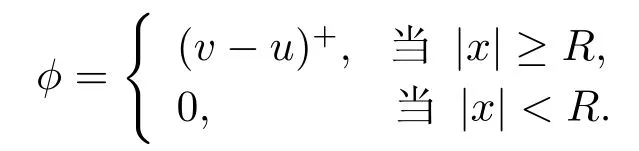
這蘊(yùn)含了? ∈E.由于v是方程(3.22)的一個(gè)解, 可推出

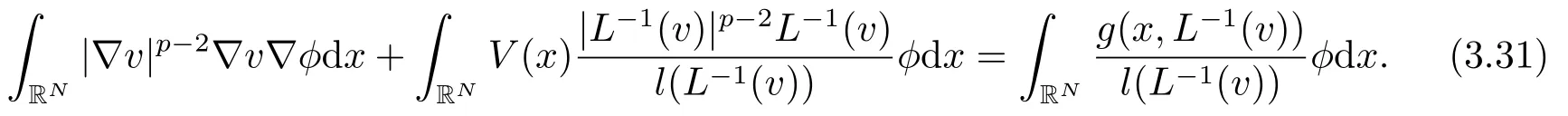
另一方面, 根據(jù)基本不等式(見文[18]中引理2.1):當(dāng)p > 1時(shí), 存在C(p) > 0, 使得對(duì)任意的η1,η2∈RN, 有

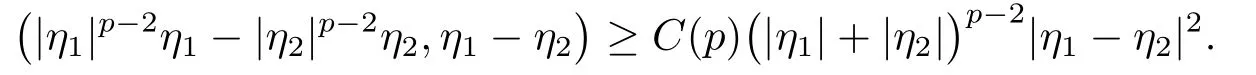
利用該不等式, 可得

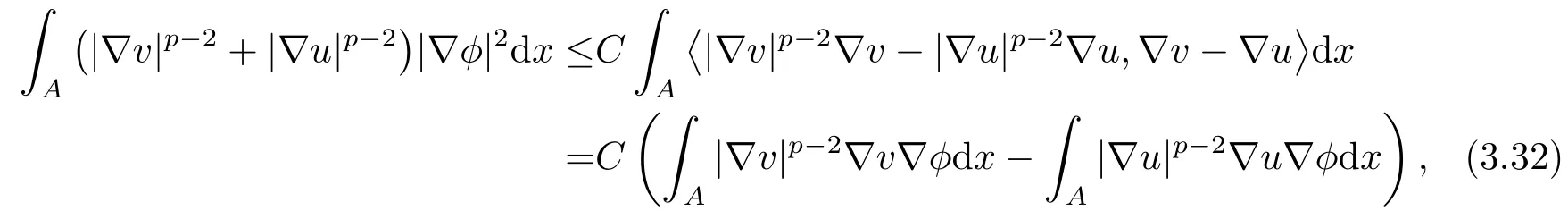
其中A={x ∈RN:|x|≥R和v(x)>u(x)}.