王銀祥

(江蘇省沭陽縣建陵高級中學(xué),223699)

試題已知復(fù)數(shù)z滿足|z|=1,則|z3+3z+2i|的最大值為( )

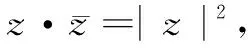
解注意到當(dāng)z=-i時,z3+3z+2i=0,從而z3+3z+2i可因式分解為z3+3z+2i=(z+i)2(z-2i).于是有|z3+3z+2i|=|z+i|2|z-2i|.聯(lián)想到復(fù)數(shù)的幾何意義,問題轉(zhuǎn)化為:如圖1,已知點(diǎn)A(0,-1),B(0,2),點(diǎn)P為圓O:x2+y2=1上一動點(diǎn), 求乘積|PA|2· |PB|的最大值.

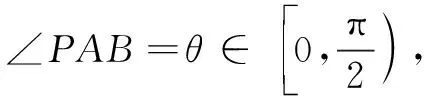
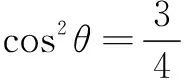
故選B.

評注通過觀察發(fā)現(xiàn)目標(biāo)式可以因式分解,這是解決本問題的關(guān)鍵.此后先利用復(fù)數(shù)模的運(yùn)算性質(zhì)、幾何意義將問題轉(zhuǎn)化為距離的乘積,再通過設(shè)輔助角為變量,運(yùn)用余弦定理轉(zhuǎn)化為三角函數(shù)模型.這種方法區(qū)別于文[1]所示的兩種求解方法,最后的函數(shù)模型可以運(yùn)用三元基本不等式求出最值,從而解決問題.