楊亮亮,張 暉,張 華,魯文其

(浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院,浙江杭州 310018)

1 引言

在高速高精度運(yùn)動(dòng)控制中,一般采用反饋加前饋的二自由度復(fù)合控制策略[1–2].其中反饋控制器用來(lái)保證系統(tǒng)的穩(wěn)定性和對(duì)擾動(dòng)及參數(shù)攝動(dòng)的魯棒性,前饋控制器用以提高系統(tǒng)響應(yīng)速度以及軌跡跟蹤性能[3–5].常見的前饋控制方法有兩種,一種是基于前饋力注入的控制方法;另外一種是基于模型的前饋控制.基于前饋力注入的前饋控制方法一般通過(guò)最優(yōu)化方法獲取最優(yōu)前饋力后將其注入到控制系統(tǒng)中以獲得最優(yōu)控制性能,但是由于最優(yōu)前饋力是軌跡的泛函,當(dāng)軌跡發(fā)生變化時(shí),需要重新計(jì)算最優(yōu)前饋力,否則會(huì)導(dǎo)致控制性能惡化[6–9],因此,基于前饋力注入的設(shè)計(jì)方法一般用于固定軌跡的重復(fù)運(yùn)動(dòng)場(chǎng)合.而基于模型的前饋控制器設(shè)計(jì)方法其前饋控制器一般為被控對(duì)象模型的逆,因此,不會(huì)因?yàn)檫\(yùn)動(dòng)軌跡的變化而導(dǎo)致性能惡化,但是當(dāng)對(duì)象為非最小相位系統(tǒng)時(shí),其模型逆是不穩(wěn)定的,基于該模型逆設(shè)計(jì)的前饋控制器會(huì)導(dǎo)致前饋力過(guò)大超出執(zhí)行器輸出范圍[1–2,7,10–11].針對(duì)這一問(wèn)題,Zou等[10,12]提出了有限時(shí)間預(yù)覽的穩(wěn)定逆的方法,但是該方法不僅要通過(guò)辨識(shí)方法獲取被控對(duì)象模型,對(duì)于復(fù)雜系統(tǒng)模型建立難度較大,而且穩(wěn)定逆逼近設(shè)計(jì)的方法相對(duì)比較復(fù)雜且對(duì)預(yù)覽時(shí)間有要求.

另一種基于模型的前饋控制方法是將前饋控制器參數(shù)化,得到的最優(yōu)參數(shù)與系統(tǒng)的模型有關(guān),同樣不會(huì)隨著軌跡的變化而變化,也能實(shí)現(xiàn)良好的跟蹤性能[13–20].該方法避免了繁瑣的模型辨識(shí)過(guò)程,并且該前饋控制器是一個(gè)穩(wěn)定的有限脈沖響應(yīng)濾波器[21–22].Boeren等[21–23]提出了引入基函數(shù)方法對(duì)前饋控制器參數(shù)化[24–25].文獻(xiàn)[21]采用基函數(shù)對(duì)前饋控制器進(jìn)行參數(shù)化,通過(guò)最小二乘法進(jìn)行最優(yōu)參數(shù)辨識(shí),并運(yùn)用在兩質(zhì)量運(yùn)動(dòng)模型上,驗(yàn)證了前饋參數(shù)化算法能夠?qū)崿F(xiàn)不依賴參數(shù)模型而實(shí)現(xiàn)較高的軌跡跟蹤性能,但是當(dāng)被控對(duì)象非單位分子時(shí),算法性能會(huì)惡化.文獻(xiàn)[23]中改進(jìn)了參數(shù)化前饋控制算法,加入了輸入整形濾波器,并對(duì)整形濾波器以及前饋控制器進(jìn)行參數(shù)化,然后再經(jīng)過(guò)最小二乘法進(jìn)行參數(shù)辨識(shí),得到參數(shù)最優(yōu)值,適用于被控對(duì)象非單位分子的情況.文獻(xiàn)[26]在輸入整形與前饋參數(shù)化的基礎(chǔ)上,通過(guò)梯度下降法求解最優(yōu)前饋控制器,并運(yùn)用于伺服控制平臺(tái),實(shí)現(xiàn)良好的變軌跡跟蹤性能.這些方法中采用最小二乘法或梯度法進(jìn)行最優(yōu)參數(shù)辨識(shí),其中最小二乘法的性能指標(biāo)只是誤差的二范數(shù),雖能夠通過(guò)一次迭代得到最優(yōu)參數(shù),但是對(duì)于執(zhí)行器受約束的情況,可能會(huì)導(dǎo)致得到的最優(yōu)前饋力超出了執(zhí)行器的輸出范圍,同樣,梯度法的性能指標(biāo)也只是誤差的二范數(shù),其只能限制誤差隨辨識(shí)參數(shù)的變化快慢,未能考慮執(zhí)行器輸出受限時(shí),前饋力超出其輸出范圍的問(wèn)題.

因此,本文在文獻(xiàn)[23]的基礎(chǔ)上提出一種改進(jìn)的前饋算法,改進(jìn)算法的最優(yōu)控制目標(biāo)函數(shù)考慮了系統(tǒng)的誤差,控制信號(hào)的迭代變化以及控制信號(hào)能量大小,通過(guò)數(shù)據(jù)驅(qū)動(dòng)的方法逐步迭代達(dá)到參數(shù)最優(yōu)值,從而適用在執(zhí)行器受約束情況下的非重復(fù)性軌跡跟蹤任務(wù),使運(yùn)動(dòng)控制系統(tǒng)在執(zhí)行器受約束時(shí)能夠?qū)崿F(xiàn)對(duì)非重復(fù)性軌跡的良好跟蹤性能.

本文結(jié)構(gòu)如下: 第2節(jié)問(wèn)題定義中介紹了參數(shù)化輸入整形濾波器與前饋控制器的前饋控制,并分析了現(xiàn)有控制方法辨識(shí)參數(shù)無(wú)約束造成的影響;第3節(jié)對(duì)改進(jìn)算法的輸入整形濾波器與前饋控制器的參數(shù)辨識(shí);第4節(jié)對(duì)改進(jìn)算法與現(xiàn)有算法進(jìn)行了比較,并對(duì)改進(jìn)算法的參數(shù)收斂性進(jìn)行了分析;第5節(jié)通過(guò)仿真與實(shí)驗(yàn)對(duì)算法進(jìn)行驗(yàn)證,并對(duì)仿真與實(shí)驗(yàn)結(jié)果進(jìn)行分析;第6節(jié)進(jìn)行總結(jié).

2 問(wèn)題定義

2.1 參數(shù)化輸入整形濾波器與前饋控制器

參數(shù)化輸入整形濾波器與前饋控制器控制系統(tǒng)框架如圖1所示.控制系統(tǒng)中輸入整形濾波器Ty對(duì)參考軌跡進(jìn)行整形,前饋控制器Tff改善伺服性能,反饋控制器Cfb保證系統(tǒng)閉環(huán)穩(wěn)定,被控對(duì)象P為離散單輸入單輸出線性時(shí)不變系統(tǒng).系統(tǒng)傳遞函數(shù)可寫為

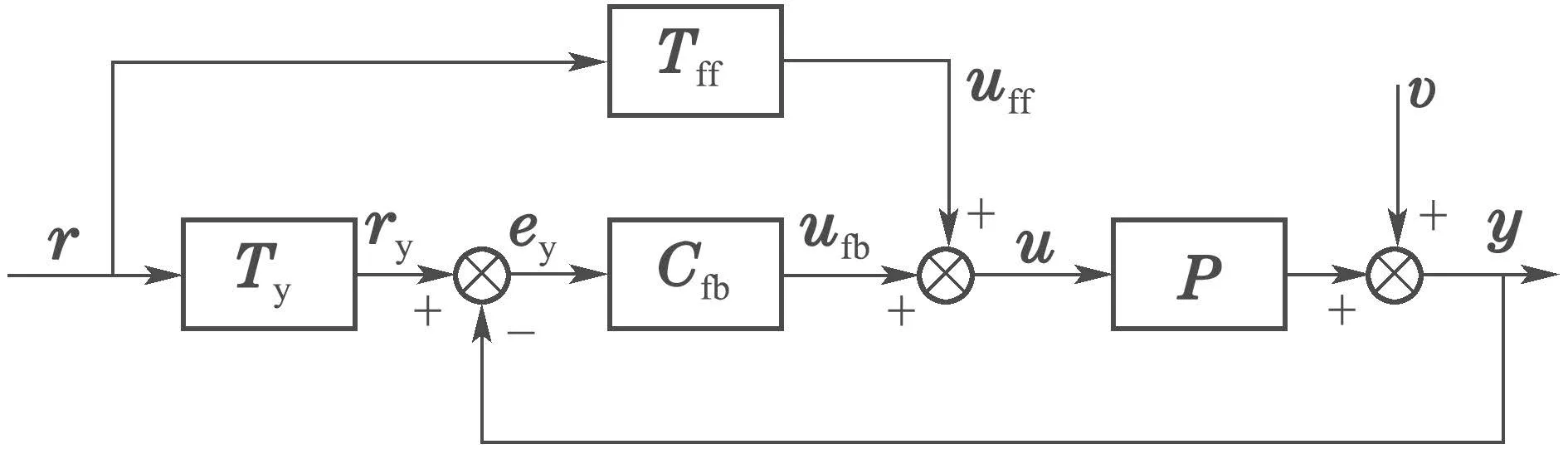
圖1 控制系統(tǒng)框架Fig.1 Control system framework

此外,r為事先規(guī)劃好的輸入軌跡信號(hào),ry為整形輸入軌跡信號(hào),y為輸出信號(hào),ey為整形輸入信號(hào)與輸出信號(hào)的誤差,uff為前饋控制信號(hào),ufb為反饋控制信號(hào),u為被控對(duì)象的控制信號(hào),v為干擾信號(hào),其中規(guī)定敏感函數(shù)為T=CfbTy+Tff,系統(tǒng)敏感函數(shù)為S=(1+P Cfb)?1.

參考輸入軌跡為S型點(diǎn)到點(diǎn)軌跡[27],如圖2所示.當(dāng)t ∈[t1,t2]時(shí),為執(zhí)行段;當(dāng)t ∈[t2,t3]時(shí),為穩(wěn)定段,其中t1為運(yùn)動(dòng)起始時(shí)刻,t2為軌跡達(dá)到終點(diǎn)時(shí)刻,t3為軌跡達(dá)到終點(diǎn)位置后經(jīng)過(guò)一段時(shí)間后的運(yùn)動(dòng)穩(wěn)定時(shí)刻.

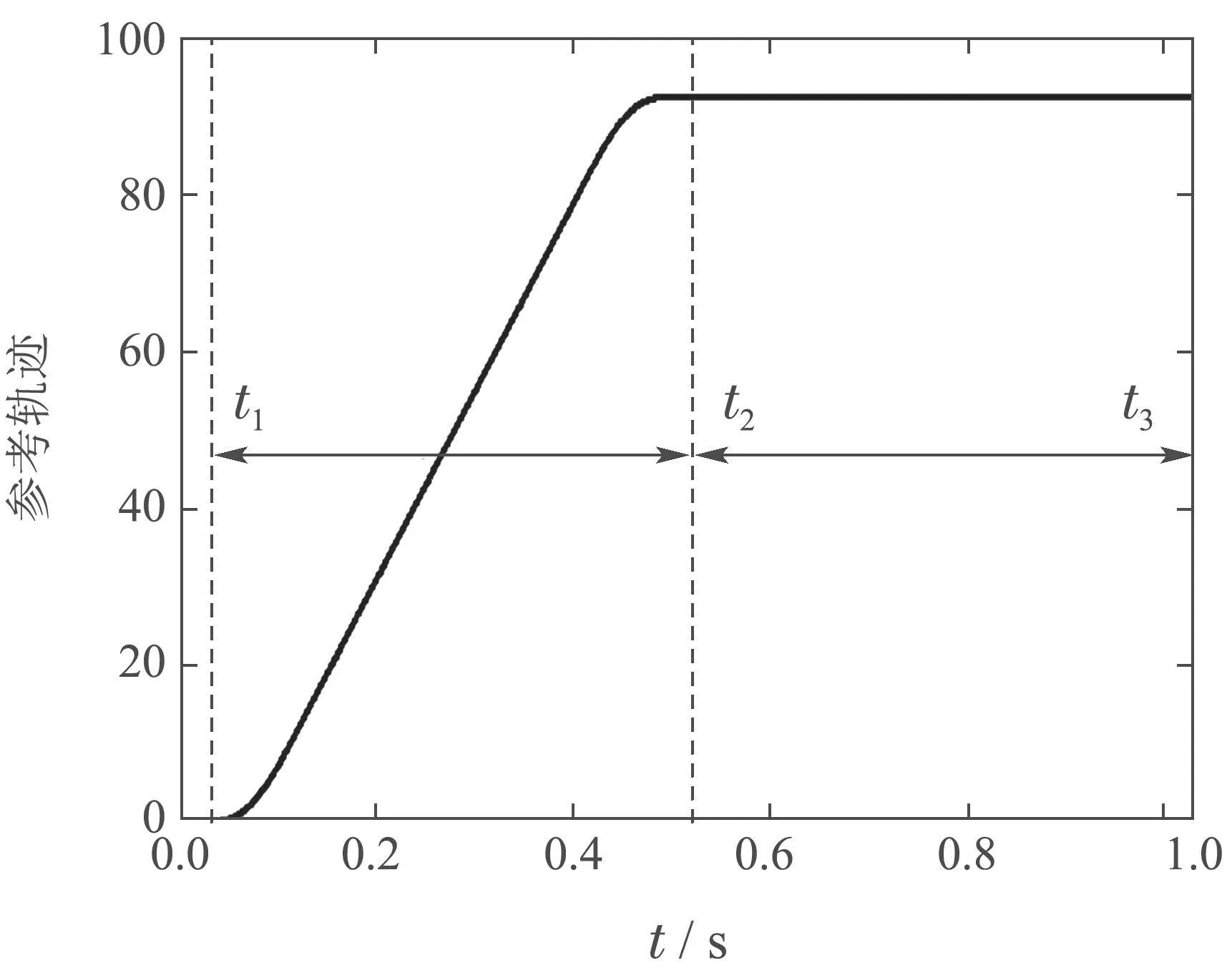
圖2 S型點(diǎn)到點(diǎn)參考軌跡Fig.2 S-shaped point-to-point reference trajectory

通過(guò)引入基函數(shù)將輸入整形濾波器Ty和前饋控制器Tff參數(shù)化為

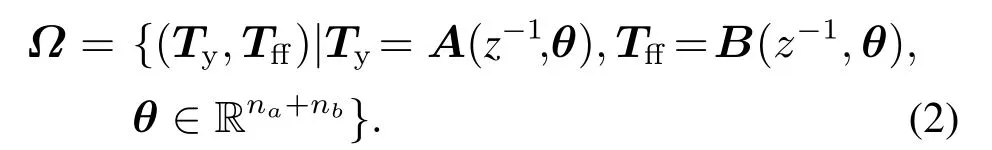
式中:

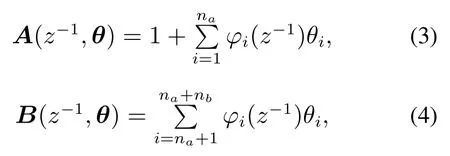
其中:A(z?1,θ),B(z?1,θ)分別為輸入整形濾波器和前饋控制器的參數(shù)化多項(xiàng)式,θ為參數(shù)化基函數(shù)多項(xiàng)式要辨識(shí)的參數(shù),na,nb為組成Ty和Tff的基函數(shù)的個(gè)數(shù),Ts為采樣時(shí)間.基函數(shù)φi(z?1)可將輸入軌跡分解為各階導(dǎo)數(shù),例如在A(z?1,θ)中的加速度基函數(shù)φ2(z?1)可表示為

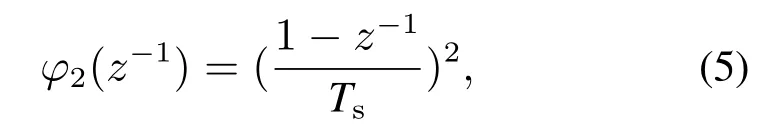
對(duì)應(yīng)的參數(shù)θ2為系統(tǒng)質(zhì)量.

為了簡(jiǎn)化符號(hào)的表達(dá),辨識(shí)參數(shù)和基函數(shù)向量形式表示為

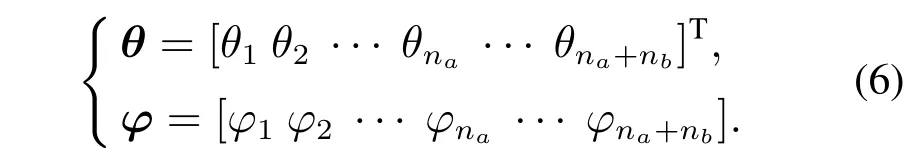
在圖1的控制框架中,第j+1次輸入整形濾波器和前饋控制器的更新公式為

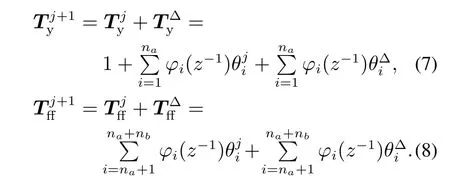
文獻(xiàn)[22–23,26,28–29]中,為了使穩(wěn)定段誤差e最小,目標(biāo)函數(shù)均定義為

由圖1可知ry=Tyr,圖2中在穩(wěn)定段時(shí)Ty|z=1=1,此時(shí)ry=r,但執(zhí)行段有一段延時(shí),延時(shí)時(shí)長(zhǎng)等于Ty中基函數(shù)的個(gè)數(shù)na.故當(dāng)t ∈[t2+na,t3]時(shí)

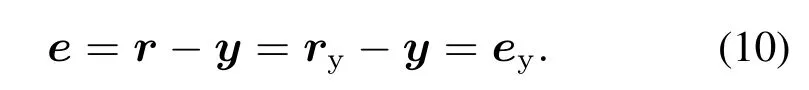
因此在穩(wěn)定段目標(biāo)函數(shù)J可寫為

由圖1可知

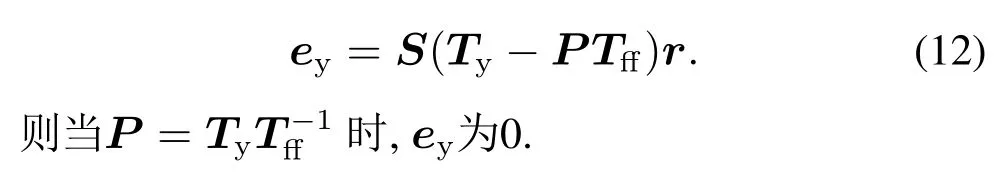
2.2 參數(shù)化前饋辨識(shí)參數(shù)無(wú)約束的影響

在文獻(xiàn)[21,23]中,根據(jù)式(11)通過(guò)最小二乘法獲得辨識(shí)參數(shù)的變化量θ?為

其中

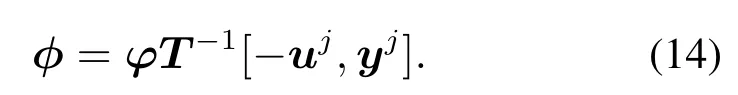
由式(13)辨識(shí)參數(shù)θ的變化量θ?是無(wú)約束的,能夠使辨識(shí)參數(shù)θ一次得到最優(yōu)值.由圖1,式(7)–(8)可知,當(dāng)θ?變化量過(guò)大可能導(dǎo)致前饋控制信號(hào)uff過(guò)大,從而造成控制信號(hào)u過(guò)大,對(duì)于執(zhí)行器受約束的系統(tǒng),控制信號(hào)過(guò)大會(huì)造成超出執(zhí)行器輸出范圍而導(dǎo)致性能惡化.

因此,一方面為了控制θ變化步長(zhǎng),另一方面為了防止控制信號(hào)u輸出過(guò)大超出執(zhí)行器的輸出范圍,本文引入新的目標(biāo)性能函數(shù)式(15),對(duì)控制信號(hào)u和控制信號(hào)變化量?u進(jìn)行約束,從而達(dá)到對(duì)辨識(shí)參數(shù)的約束.

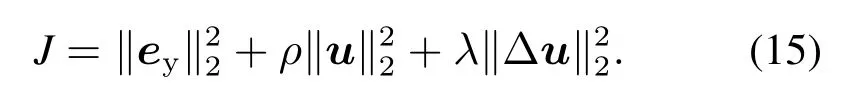
3 改進(jìn)算法的參數(shù)辨識(shí)

迭代控制系統(tǒng)框架如圖1所示,在不考慮干擾v的情況下,由第j次迭代測(cè)量得到,uj,yj的數(shù)據(jù),可得

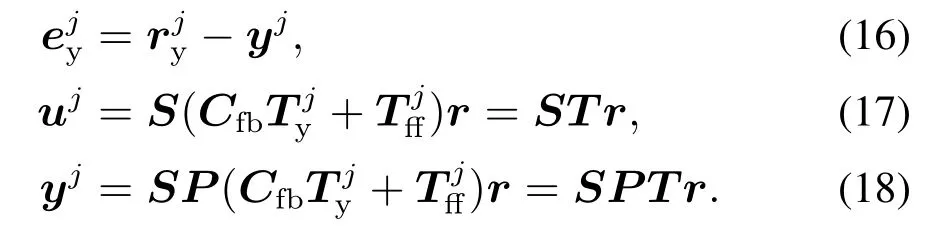
S與SP都跟參數(shù)模型有關(guān),為了消除對(duì)模型的依賴,根據(jù)式(17)–(18)將其轉(zhuǎn)化為基于數(shù)據(jù)驅(qū)動(dòng)的形式

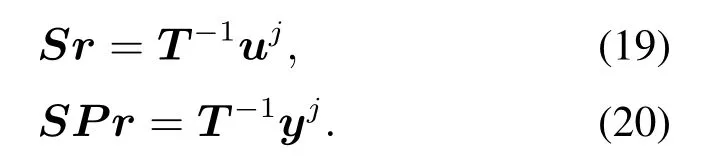
在第j+1次迭代,由上述式子可知

參數(shù)的最小二乘估計(jì),就是使目標(biāo)函數(shù)J取極小值的參數(shù)θ?.使上式(32)取得極小值,求J對(duì)θ?的一階導(dǎo)數(shù),并令其為0,則

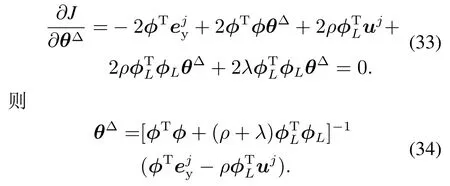
其中:λ為控制信號(hào)變化量的約束參數(shù),ρ是控制信號(hào)的約束參數(shù).要得到?,?L需要求解T?1,如果T?1不穩(wěn)定,可通過(guò)文獻(xiàn)[7,10]中方法進(jìn)行穩(wěn)定逆逼近,也可參考文獻(xiàn)[11]中3種穩(wěn)定近似逆進(jìn)行求解,相對(duì)于穩(wěn)定逆逼近,穩(wěn)定近似逆設(shè)計(jì)更為簡(jiǎn)單,本文對(duì)于不穩(wěn)定逆采用穩(wěn)定近似逆的零相位誤差跟蹤技術(shù)[11,28].

4 改進(jìn)算法的分析

4.1 改進(jìn)算法與現(xiàn)有算法的比較

文獻(xiàn)[21,23]中最小二乘法辨識(shí)參數(shù)如式(13)所示,文獻(xiàn)[26,29–30]中采用梯度下降法求解最優(yōu)前饋控制器,通過(guò)計(jì)算誤差ey對(duì)辨識(shí)參數(shù)的梯度值,來(lái)求解最優(yōu)參數(shù)值,其迭代學(xué)習(xí)律為

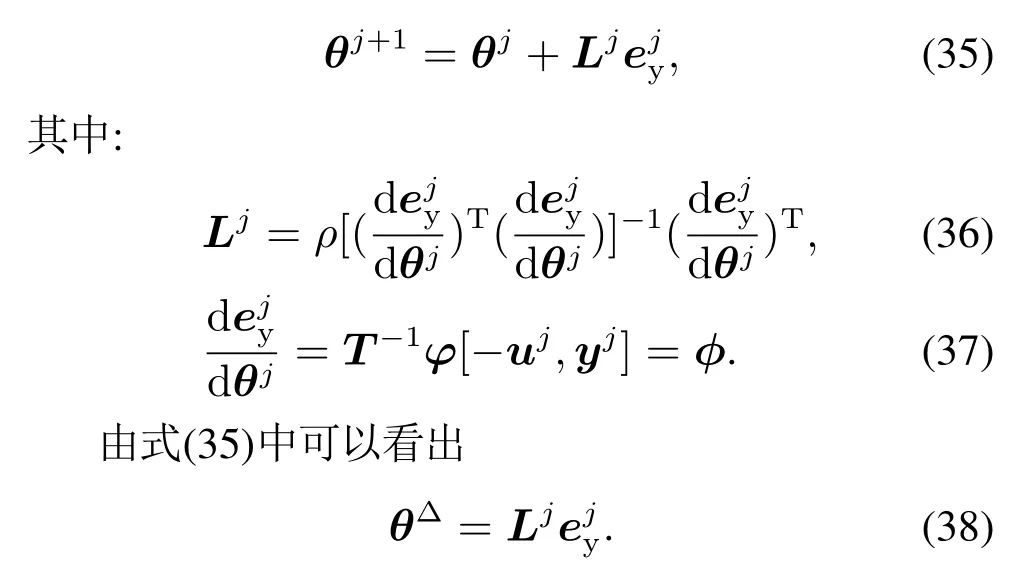
由式(13)(34)(38)可知,現(xiàn)有的最小二乘法是無(wú)約束的,未考慮執(zhí)行器的執(zhí)行能力,梯度下降法直接通過(guò)ρ影響辨識(shí)參數(shù)變化量θ?的收斂速度,相對(duì)于現(xiàn)有方法,本文算法是針對(duì)執(zhí)行器有約束的情況,通過(guò)約束參數(shù)λ和ρ直接限制控制信號(hào)變化量和控制能量的大小,同時(shí)間接的去約束辨識(shí)參數(shù)變化量θ?來(lái)影響辨識(shí)參數(shù)θ的收斂速度和收斂值,可以更直接有效防止執(zhí)行器超出輸出范圍.

4.2 改進(jìn)算法的收斂性

輸入整形濾波器Ty和前饋控制器Tff均為有限脈沖響應(yīng)濾波器,而在式(25)中誤差ey與有限脈沖響應(yīng)濾波器參數(shù)成線性關(guān)系,由文獻(xiàn)[15,26]可知誤差ey是全局收斂的.由式(25)可知

因此可知,辨識(shí)參數(shù)θ收斂.

由式(34)可知通過(guò)調(diào)整約束參數(shù)λ和參數(shù)ρ,即可約束θ的變化量,當(dāng)λ=0且ρ=0時(shí),即是退化為式(13)的最小二乘算法.當(dāng)ρ保持不變,λ取值越大,θ變化量越小,θ收斂到最優(yōu)值越慢,系統(tǒng)前饋控制信號(hào)達(dá)到最優(yōu)值的速度越慢,從而使得誤差收斂速度越慢,反之,則收斂速度越快.當(dāng)λ保持不變,ρ越大,對(duì)控制信號(hào)約束作用越大,辨識(shí)參數(shù)變化量越小,誤差收斂值越大,反之誤差收斂值越小.

4.3 算法實(shí)現(xiàn)步驟

綜上所述,改進(jìn)的前饋參數(shù)化算法實(shí)現(xiàn)步驟如下:

1) 選取θ初值和合適的約束參數(shù)λ和ρ.

2) 測(cè)量,uj,yj的值.

3) 通過(guò)測(cè)量值uj,yj計(jì)算

6) 不斷重復(fù)步驟2)–5),直到系統(tǒng)收斂到最優(yōu)跟蹤性能.

5 仿真與實(shí)驗(yàn)

5.1 仿真設(shè)計(jì)與結(jié)果

采用MATLAB/Simulink對(duì)上述控制算法進(jìn)行仿真.仿真時(shí)參考軌跡采用四階S型點(diǎn)到點(diǎn)軌跡規(guī)劃如圖3所示.仿真對(duì)象模型如下所示:

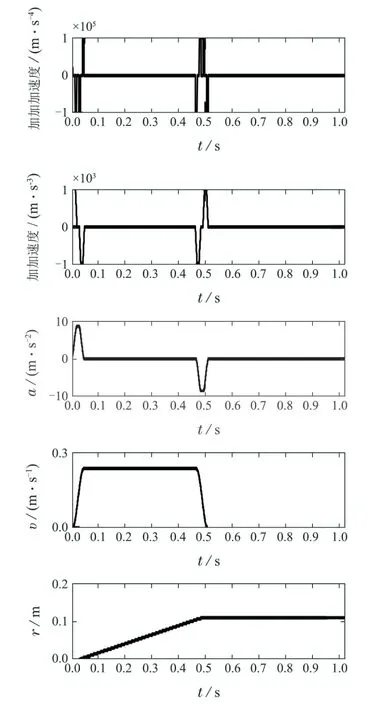
圖3 四階S型點(diǎn)到點(diǎn)軌跡Fig.3 Fourth-order S-shaped point-to-point trajectory

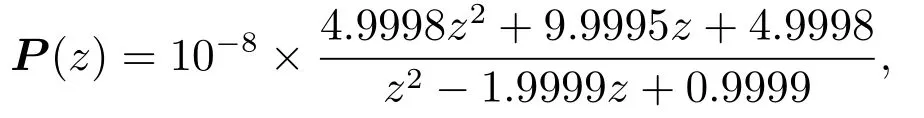
其中采樣時(shí)間為Ts=5.0×10?4s.

反饋控制器Cfb為

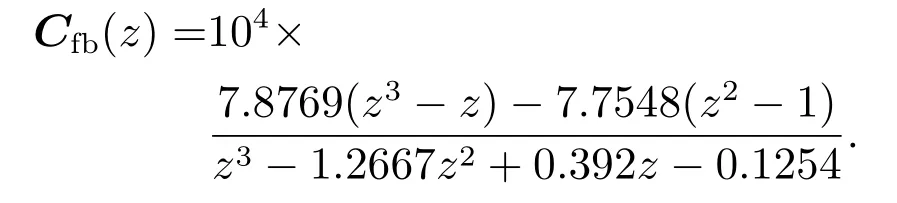
建立輸入整形濾波器Ty和前饋制器Tff參數(shù)化多項(xiàng)式為

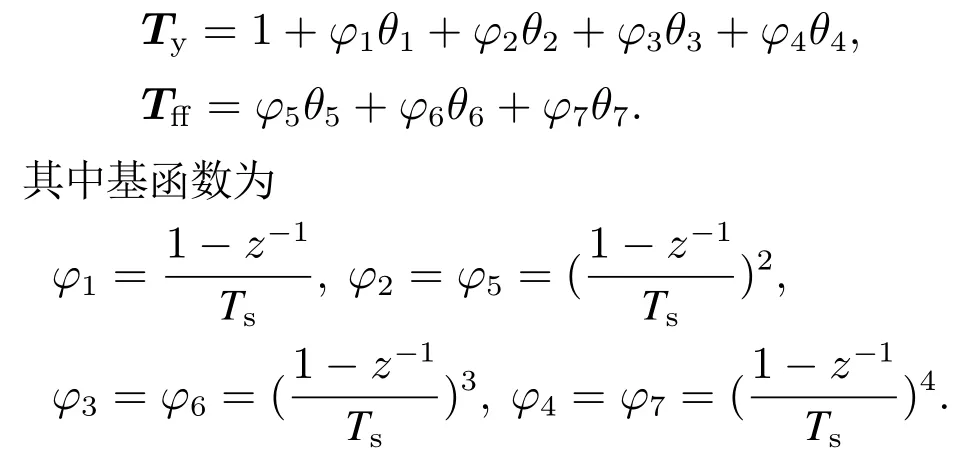
選取初始值θ1=[0 0 0 0 0.1 0 0]T,仿真實(shí)驗(yàn)的執(zhí)行器的輸出范圍選為?25 N～25 N.

圖4為當(dāng)約束參數(shù)ρ保持不變,只考慮約束參數(shù)λ變化時(shí),穩(wěn)定段誤差的二范數(shù)隨迭代次數(shù)變化的曲線.由圖可知當(dāng)ρ=1×10?10時(shí),λ越小,穩(wěn)定段誤差二范數(shù)衰減到最優(yōu)的速度越快.

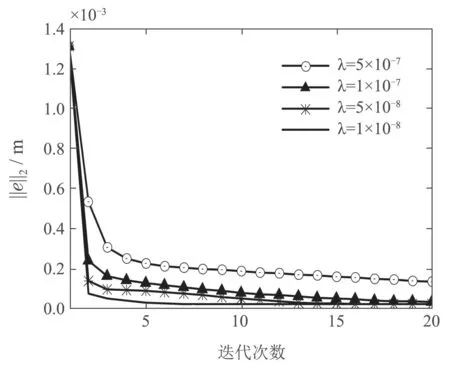
圖4 ρ=1×10?10時(shí),約束參數(shù)λ對(duì)誤差二范數(shù)的影響曲線Fig.4 Curve of the effect for the constraint parameter λ on the two-norm for the error when ρ=1×10?10

圖5為當(dāng)約束參數(shù)λ保持不變時(shí),只考慮約束參數(shù)ρ變化時(shí),穩(wěn)定段誤差的二范數(shù)隨迭代次數(shù)變化的曲線.由圖可知當(dāng)λ=1×10?8時(shí),ρ越小,穩(wěn)定段誤差二范數(shù)收斂值越小.

圖5 λ=1×10?8時(shí),約束參數(shù)ρ 對(duì)誤差二范數(shù)的影響曲線Fig.5 Curve of the effect for the constraint parameter ρ on the two-norm for the error when λ=1×10?8

表1為當(dāng)約束參數(shù)λ保持不變時(shí),不同約束參數(shù)ρ下的控制信號(hào)最大值,由表可知當(dāng)λ=1×10?8時(shí),ρ越小控制信號(hào)的最大值越大;從上述兩個(gè)試驗(yàn)可以看出通過(guò)約束參數(shù)λ可以調(diào)整算法的迭代收斂速度,通過(guò)約束參數(shù)ρ可以調(diào)整算法迭代收斂最優(yōu)值與控制信號(hào)最大值的大小.

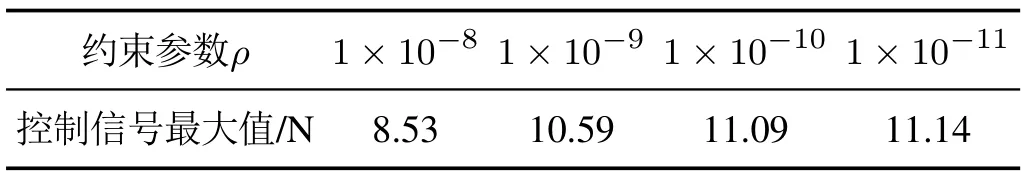
表1 不同約束參數(shù)ρ 下的控制信號(hào)最大值(λ=1×10?8)Table 1 The maximum value of the control signal with different constraint parametersρ(λ=1×10?8)

因此,執(zhí)行器受約束的運(yùn)動(dòng)控制系統(tǒng)在運(yùn)用改進(jìn)算法時(shí),可以根據(jù)執(zhí)行器的輸出范圍選擇合適的約束參數(shù)λ和ρ,來(lái)調(diào)整所提出算法的收斂速度和所需的控制信號(hào).

整段軌跡的迭代前后誤差ey如圖6所示.圖7為迭代前后的穩(wěn)定段誤差e變化曲線.由圖可知,第1次迭代時(shí)最大軌跡跟蹤誤差為10?4m量級(jí),第20次迭代時(shí)最大軌跡跟蹤誤差降為10?6m量級(jí).上述仿真實(shí)驗(yàn)結(jié)果表明改進(jìn)算法實(shí)現(xiàn)了當(dāng)前約束參數(shù)下(λ=1×10?8,ρ=1×10?10)不超出執(zhí)行器輸出范圍的軌跡最優(yōu)跟蹤性能.

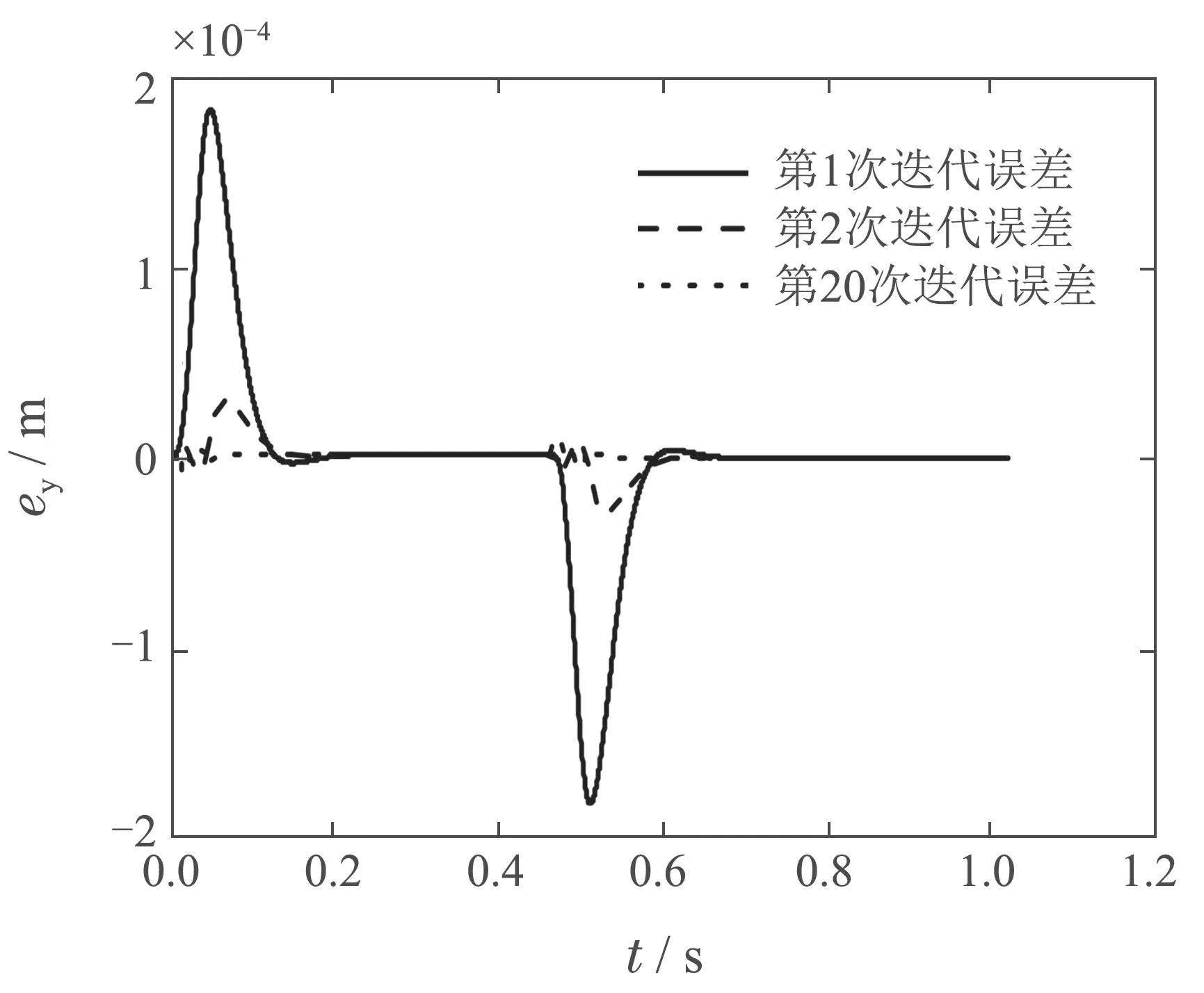
圖6 λ=1×10?8,ρ=1×10?10時(shí),迭代誤差比較Fig.6 Comparison of iterative errors when λ=1×10?8,ρ=1×10?10

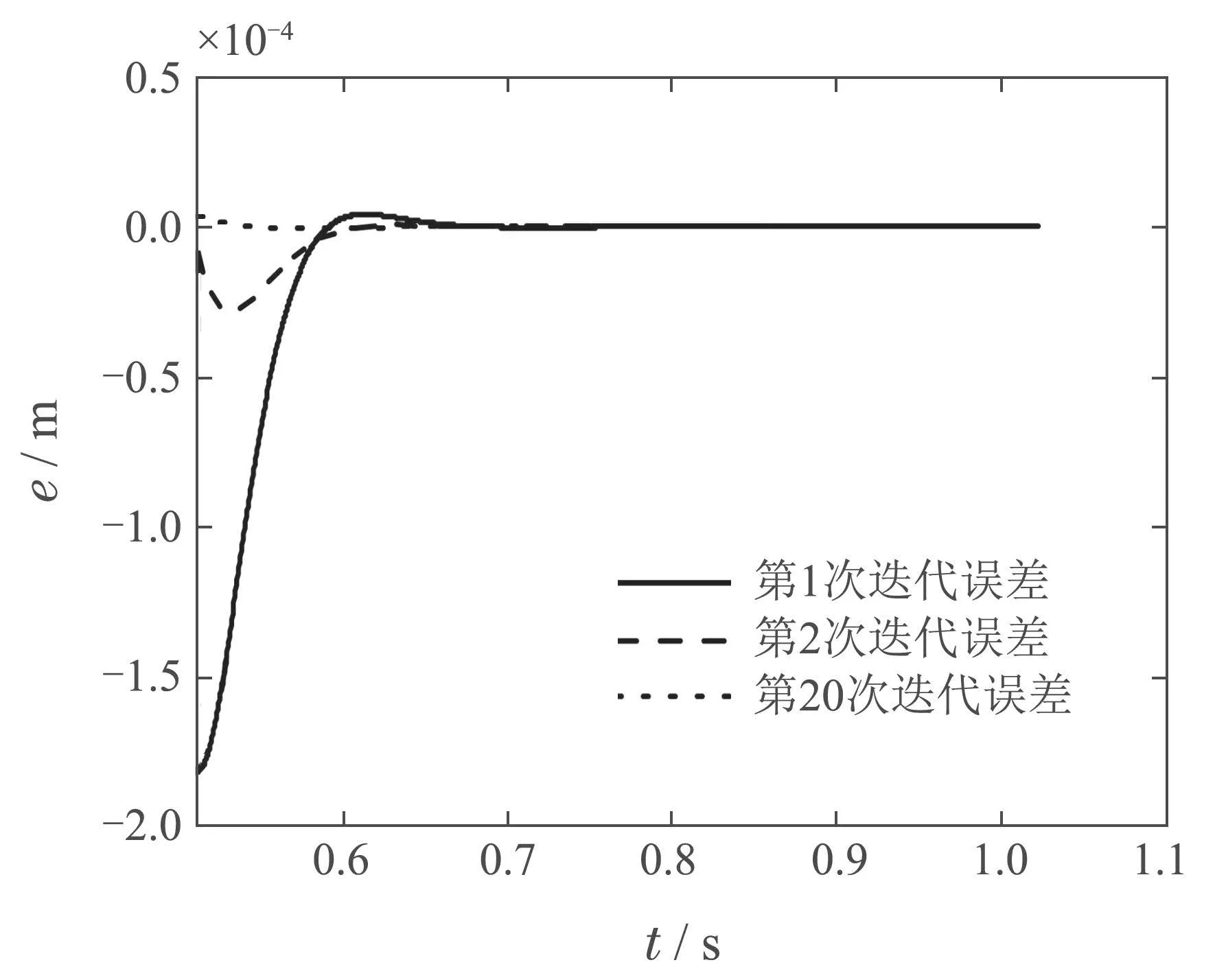
圖7 λ=1×10?8,ρ=1×10?10時(shí),穩(wěn)定段迭代誤差比較Fig.7 Comparison of iterative errors in the settling section when λ=1×10?8,ρ=1×10?10

辨識(shí)參數(shù)θ變化曲線如圖8所示,由圖可知,辨識(shí)參數(shù)θ1～θ7在第7次迭代后收斂到最優(yōu)值,最優(yōu)值如表2所示,該結(jié)果驗(yàn)證了改進(jìn)算法辨識(shí)參數(shù)的收斂性.

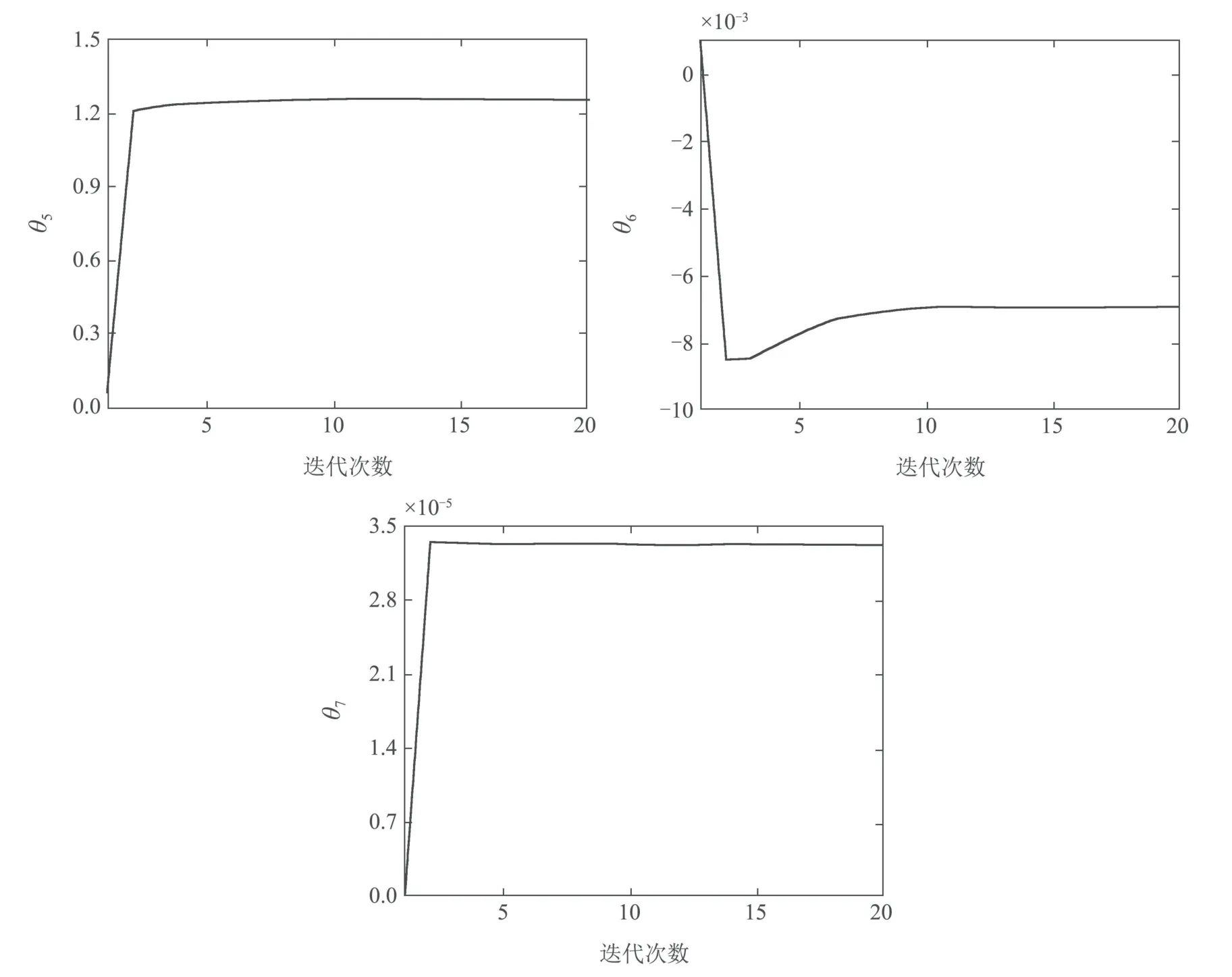
圖8 λ=1×10?8,ρ=1×10?10時(shí),辨識(shí)參數(shù)θ 變化曲線Fig.8 The variation curve of identification parameter θ when λ=1×10?8,ρ=1×10?10

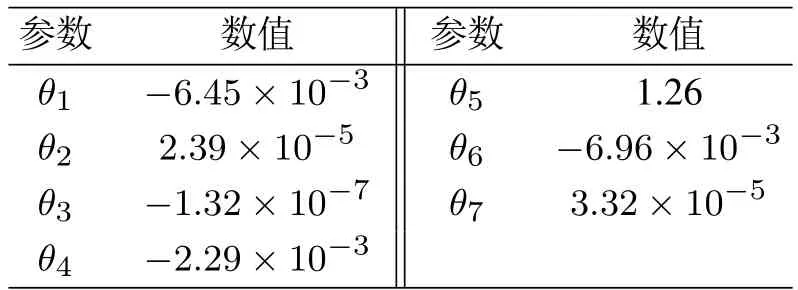
表2 參數(shù)θ最優(yōu)值(λ=1×10?8,ρ=1×10?10)Table 2 The optimal value of the parameter θ(λ=1×10?8,ρ=1×10?10)

5.2 所提出算法與現(xiàn)有算法比較

圖9為文獻(xiàn)[17]中現(xiàn)有無(wú)約束參數(shù)的算法(λ=0,ρ=0)與所提出有約束參數(shù)的改進(jìn)算法(挑選λ=1×10?8,ρ=1×10?10)控制信號(hào)曲線的比較圖.由圖可知,在無(wú)約束參數(shù)算法運(yùn)行的情況下,控制信號(hào)最大值超出執(zhí)行器輸出范圍?25 N～25 N,加入約束后的改進(jìn)算法控制信號(hào)最大值未超出執(zhí)行器輸出范圍.

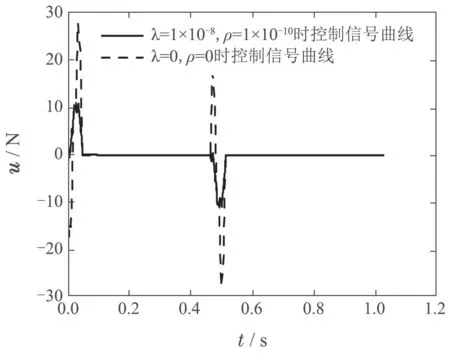
圖9 加入約束參數(shù)前后的控制信號(hào)u的比較Fig.9 Comparison of control signals u before and after adding constraint parameters

5.3 實(shí)驗(yàn)驗(yàn)證

本文的實(shí)驗(yàn)平臺(tái)為圖10所示兩個(gè)直線電動(dòng)機(jī)構(gòu)成的X-Y運(yùn)動(dòng)平臺(tái),兩個(gè)直線電動(dòng)機(jī)均采用Baldor公司的LMCF02C-HCO,電動(dòng)機(jī)的連續(xù)推力為58 N,峰值推力為173 N,直線電動(dòng)機(jī)的運(yùn)動(dòng)位置由GSI公司分辨率為0.5μm的光柵尺測(cè)量,讀數(shù)頭型號(hào)為MII1600-40.伺服驅(qū)動(dòng)器為Baldor公司的FMH2A03TR-EN23,采用電流控制方式.由于位于上層直線電動(dòng)機(jī)具有相對(duì)較低的慣量,為了驗(yàn)證高速高精性能,實(shí)際試驗(yàn)時(shí)采用下層直線電動(dòng)機(jī)鎖死,只對(duì)上層直線電動(dòng)機(jī)進(jìn)行試驗(yàn).由于電動(dòng)機(jī)的連續(xù)推力為58 N,因此為了保證實(shí)驗(yàn)的安全性和驗(yàn)證算法的有效性,實(shí)驗(yàn)平臺(tái)的執(zhí)行器的推力輸出范圍選為?60 N～60 N.

圖10 直線伺服電機(jī)實(shí)驗(yàn)平臺(tái)Fig.10 Linear servo motor experiment platform

實(shí)驗(yàn)的反饋控制器采用PID反饋控制,其參數(shù)如表3所示.

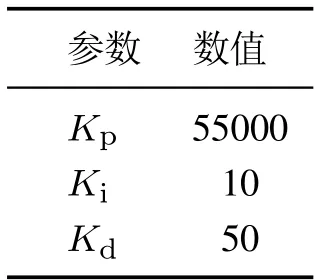
表3 PID參數(shù)Table 3 PID parameters

實(shí)驗(yàn)采用參考軌跡如圖11所示,四階S型點(diǎn)到點(diǎn)軌跡,伺服采樣時(shí)間為5×10?4s,迭代運(yùn)行20次,參數(shù)初始值θ1=[0 0 0 0 0.1 0 0]T,輸入整形濾波器和前饋控制器參數(shù)化多項(xiàng)式與仿真實(shí)驗(yàn)一致,實(shí)驗(yàn)過(guò)程中采集輸出軌跡,誤差和控制信號(hào)數(shù)據(jù).

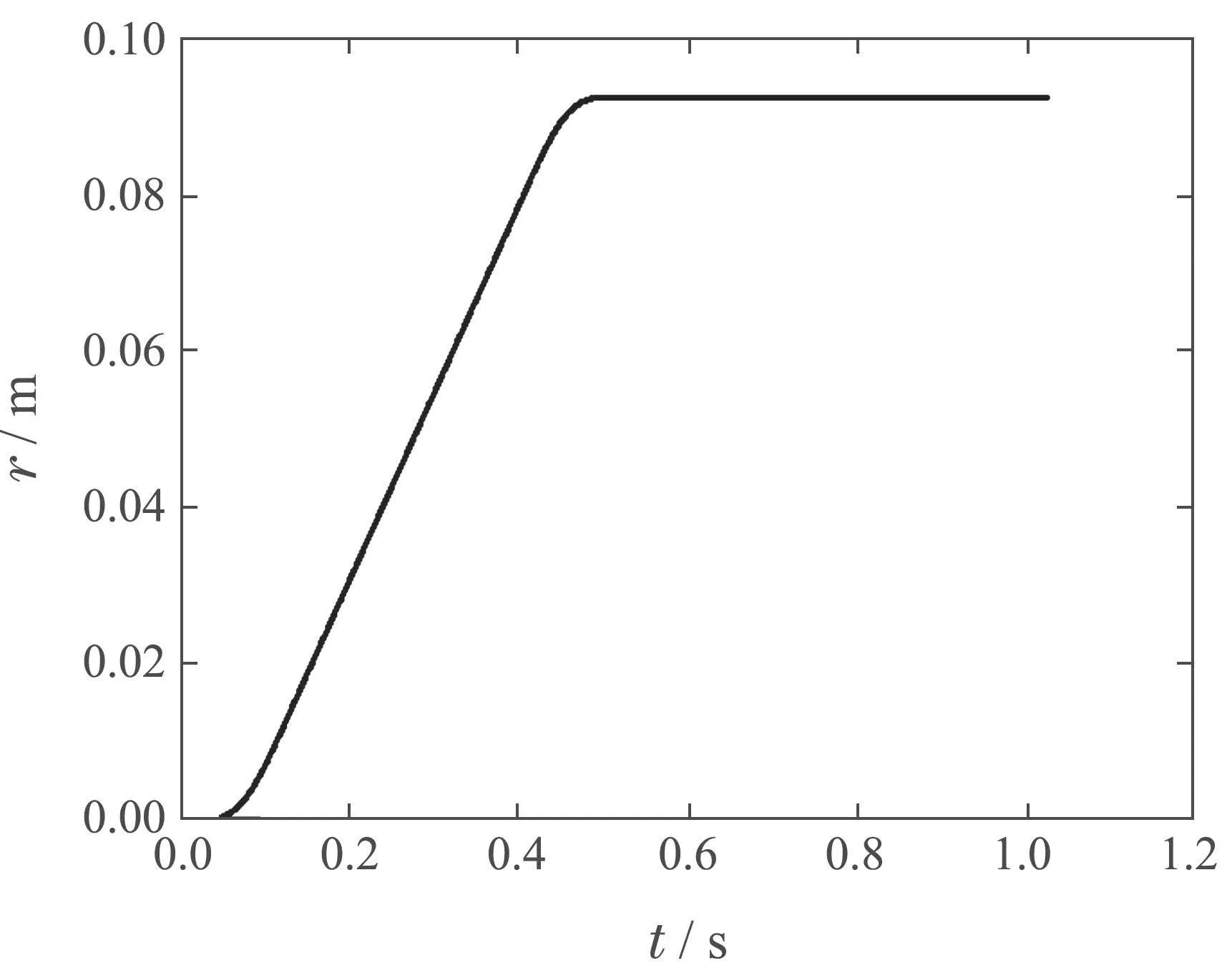
圖11 四階S型點(diǎn)到點(diǎn)參考軌跡Fig.11 Fourth-order S-shaped point-to-point reference trajectory

圖12為當(dāng)約束參數(shù)ρ保持不變時(shí),只考慮約束參數(shù)λ變化時(shí),穩(wěn)定段誤差的二范數(shù)隨迭代次數(shù)變化的曲線.由圖可知當(dāng)ρ=1×10?6時(shí),λ越小,穩(wěn)定段誤差二范數(shù)衰減到最優(yōu)的速度越快.圖13為當(dāng)約束參數(shù)λ保持不變時(shí),只考慮約束參數(shù)ρ變化時(shí),穩(wěn)定段誤差的二范數(shù)隨迭代次數(shù)變化的曲線,由圖可知當(dāng)λ=0.001時(shí),ρ越小,穩(wěn)定段誤差二范數(shù)的收斂值越小.

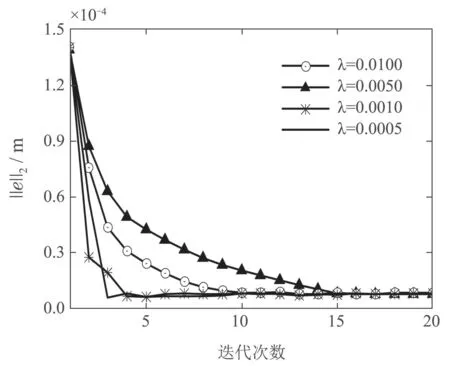
圖12 ρ=1×10?6時(shí),約束參數(shù)λ對(duì)誤差二范數(shù)的影響曲線Fig.12 Curve of the effect for the constraint parameter λ on the two-norm for the error when ρ=1×10?6

圖13 λ=0.001時(shí),約束參數(shù)ρ對(duì)誤差二范數(shù)的影響曲線Fig.13 Curve of the effect for the constraint parameter ρ on the two-norm for the error when λ=0.001

表4為當(dāng)約束參數(shù)λ保持不變時(shí),不同約束參數(shù)ρ下的控制信號(hào)最大值,由表可知當(dāng)λ=0.001時(shí),ρ越小控制信號(hào)的最大值越大.上述實(shí)驗(yàn)結(jié)果與仿真實(shí)驗(yàn)結(jié)果一致,表明了算法可以通過(guò)約束參數(shù)λ調(diào)整算法的迭代收斂速度,通過(guò)約束參數(shù)ρ調(diào)整算法迭代收斂最優(yōu)值與控制信號(hào)最大值的大小.

表4 不同約束參數(shù)ρ下的控制信號(hào)最大值(λ=0.001)Table 4 The maximum value of the control signal with different constraint parameters ρ(λ=0.001)

整段軌跡的迭代前后誤差ey如圖14所示.圖15為穩(wěn)定段迭代前后的誤差e變化曲線,由圖可知,實(shí)驗(yàn)效果與仿真一致,由第1次、第2 次和第20 次穩(wěn)定段誤差的變化趨勢(shì)可知,穩(wěn)定段誤差得到了明顯的抑制,表明了改進(jìn)算法能夠?qū)崿F(xiàn)在當(dāng)前約束參數(shù)下(λ=0.001,ρ=1×10?6)不超出執(zhí)行器輸出范圍的軌跡最優(yōu)跟蹤性能.

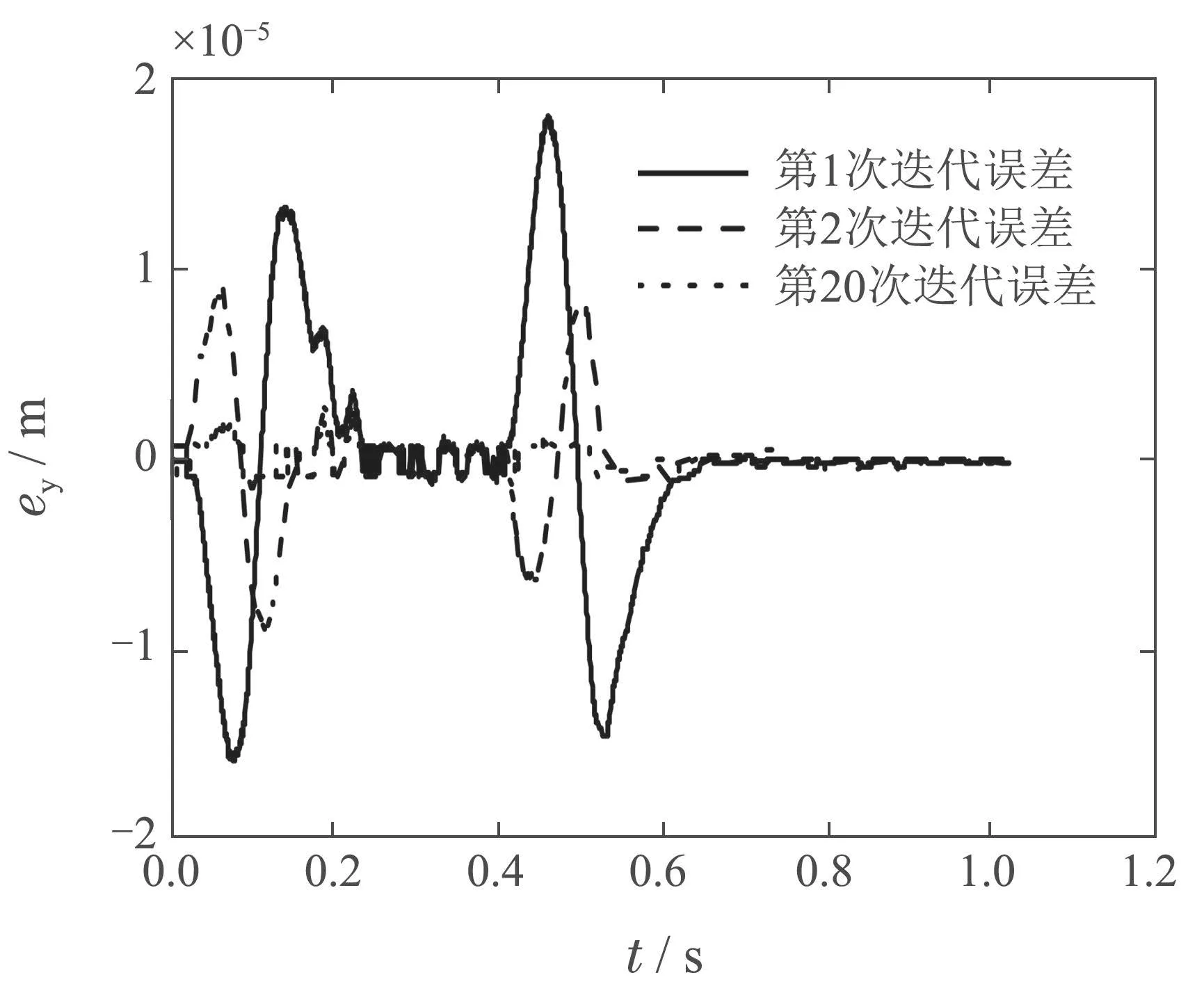
圖14 λ=0.001,ρ=1×10?6 時(shí),迭代誤差比較Fig.14 Comparison of iterative errors when λ=0.001,ρ=1×10?6

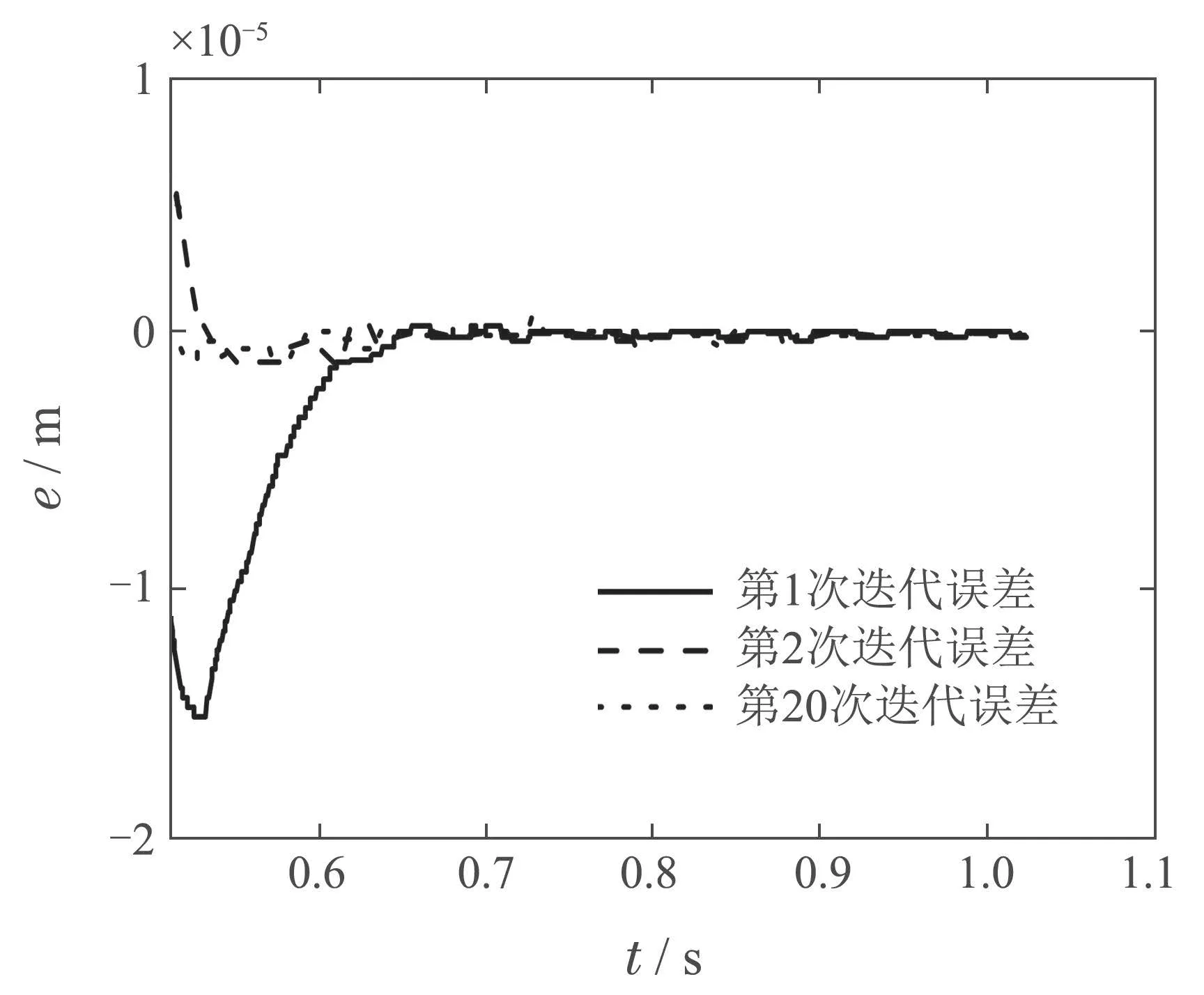
圖15 λ=0.001,ρ=1×10?6 時(shí),穩(wěn)定段迭代誤差比較Fig.15 Comparison of iterative errors in the settling section when λ=0.001,ρ=1×10?6

辨識(shí)參數(shù)θ變化曲線,如圖16所示,由圖可知,辨識(shí)參數(shù)θ1～θ7在第5次迭代收斂到最優(yōu)值,辨識(shí)參數(shù)的最優(yōu)值如表5所示.實(shí)驗(yàn)結(jié)果進(jìn)一步驗(yàn)證了改進(jìn)算法辨識(shí)參數(shù)的收斂性.

表5 參數(shù)θ 最優(yōu)值(λ=0.001,ρ=1×10?6)Table 5 The optimal value of the parameter θ(λ=0.001,ρ=1×10?6)

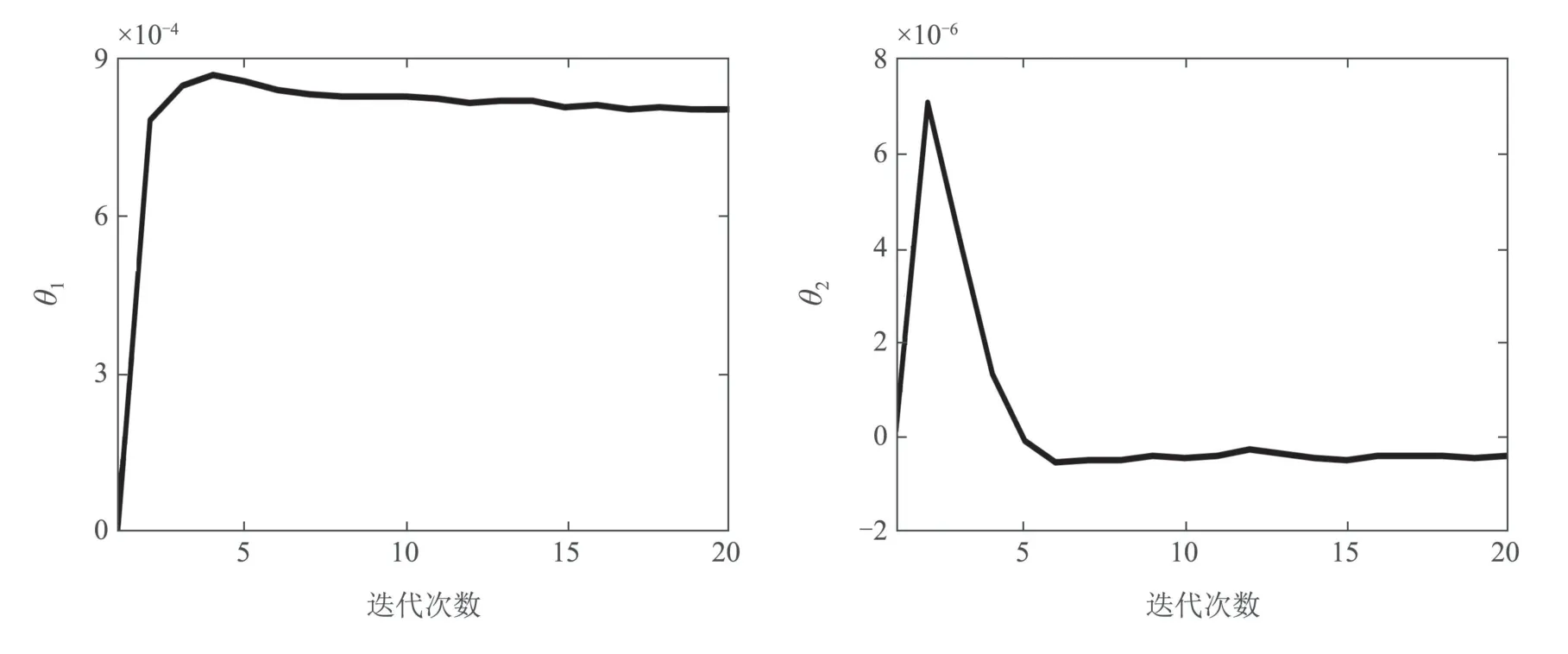
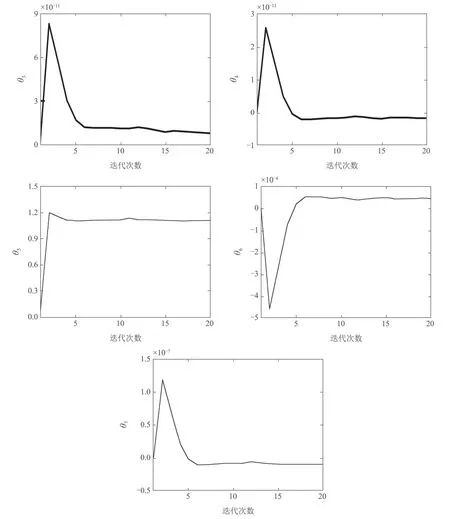
圖16 λ=0.001,ρ=1×10?6 時(shí),辨識(shí)參數(shù)θ變化曲線Fig.16 The variation curve of identification parameter θ when λ=0.001,ρ=1×10?6

5.4 非重復(fù)性軌跡實(shí)驗(yàn)

為了驗(yàn)證改進(jìn)算法在執(zhí)行器約束下對(duì)非重復(fù)性軌跡的性能,實(shí)驗(yàn)選用的參考軌跡如圖17所示.非重復(fù)性軌跡實(shí)驗(yàn),前10次迭代采用圖中參考軌跡1,后10次迭代采用參考軌跡2.該實(shí)驗(yàn)采用與上述實(shí)驗(yàn)同樣的控制結(jié)構(gòu)、伺服采樣時(shí)間和初值,約束參數(shù)選為λ=0.001,ρ=1×10?6.

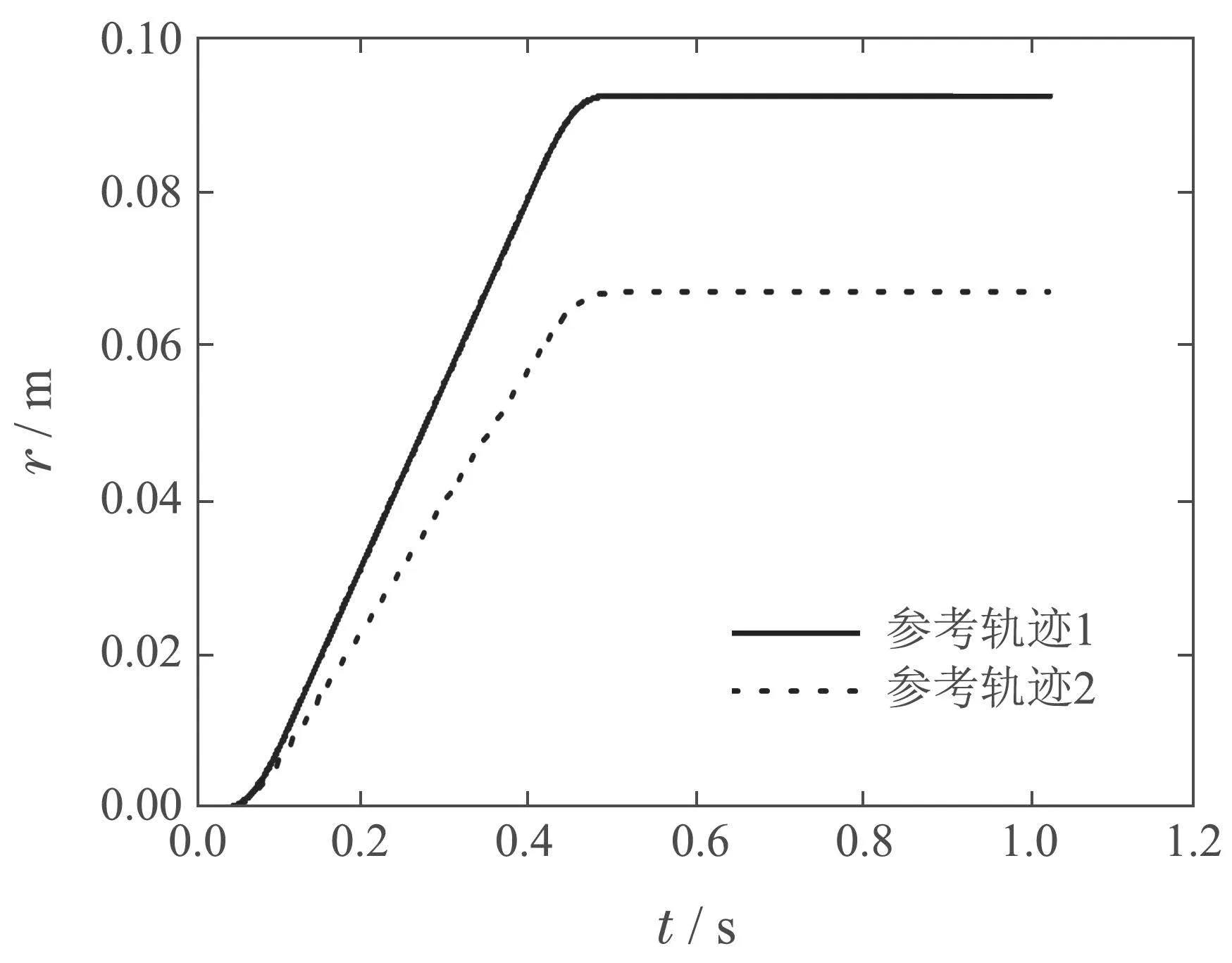
圖17 非重復(fù)性軌跡實(shí)驗(yàn)中四階S型點(diǎn)到點(diǎn)參考軌跡1和2Fig.17 Fourth-order S-shaped point-to-point reference trajectories 1 and 2 in non-repetitive trajectory experiment

非重復(fù)性軌跡實(shí)驗(yàn)中,穩(wěn)定段誤差二范數(shù)變化曲線如圖18所示,前10次迭代穩(wěn)定段誤差二范數(shù)收斂到最優(yōu)值,在第11次迭代軌跡發(fā)生變化時(shí),穩(wěn)定段誤差二范數(shù)的值略微上升,但與軌跡1性能差別不大,在經(jīng)過(guò)一次迭代后又收斂到最優(yōu)值,與軌跡1時(shí)的最優(yōu)性能一致.

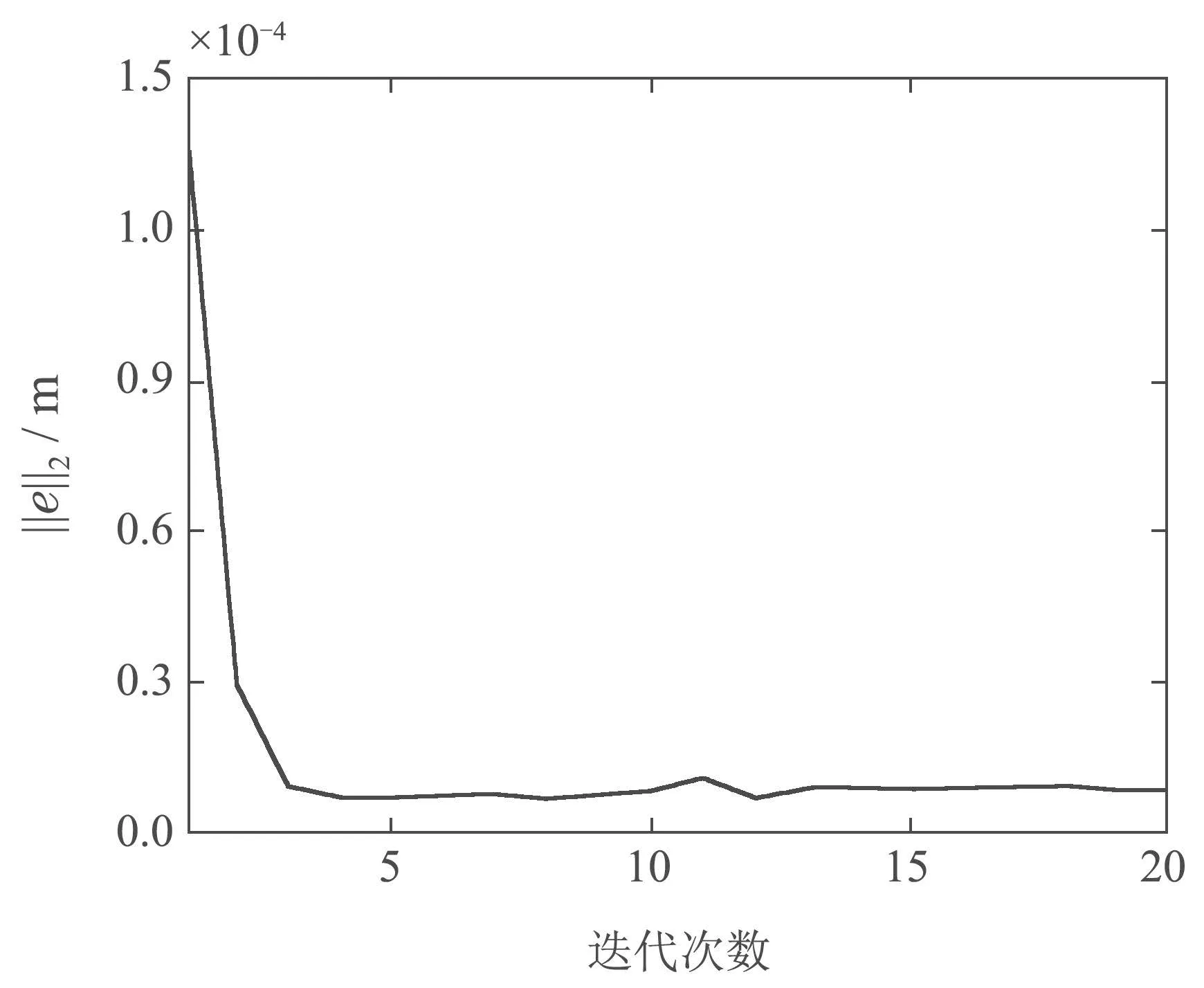
圖18 非重復(fù)性軌跡實(shí)驗(yàn)誤差二范數(shù)的變化曲線Fig.18 The variation curve of the two-norm error for the non-repetitive trajectory experiment

非重復(fù)性點(diǎn)到點(diǎn)軌跡運(yùn)動(dòng)實(shí)驗(yàn)中,運(yùn)行軌跡1達(dá)到收斂時(shí)的控制信號(hào)曲線如圖19所示,運(yùn)行軌跡2 達(dá)到收斂時(shí)的控制信號(hào)曲線如圖20所示.由圖可知,兩條軌跡運(yùn)行達(dá)到收斂時(shí)的控制信號(hào)最大值均為未超出執(zhí)行器的輸出范圍.非重復(fù)性軌跡實(shí)驗(yàn)結(jié)果表明了改進(jìn)算法在執(zhí)行器約束下對(duì)非重復(fù)性點(diǎn)到點(diǎn)軌跡具有一定的魯棒性.

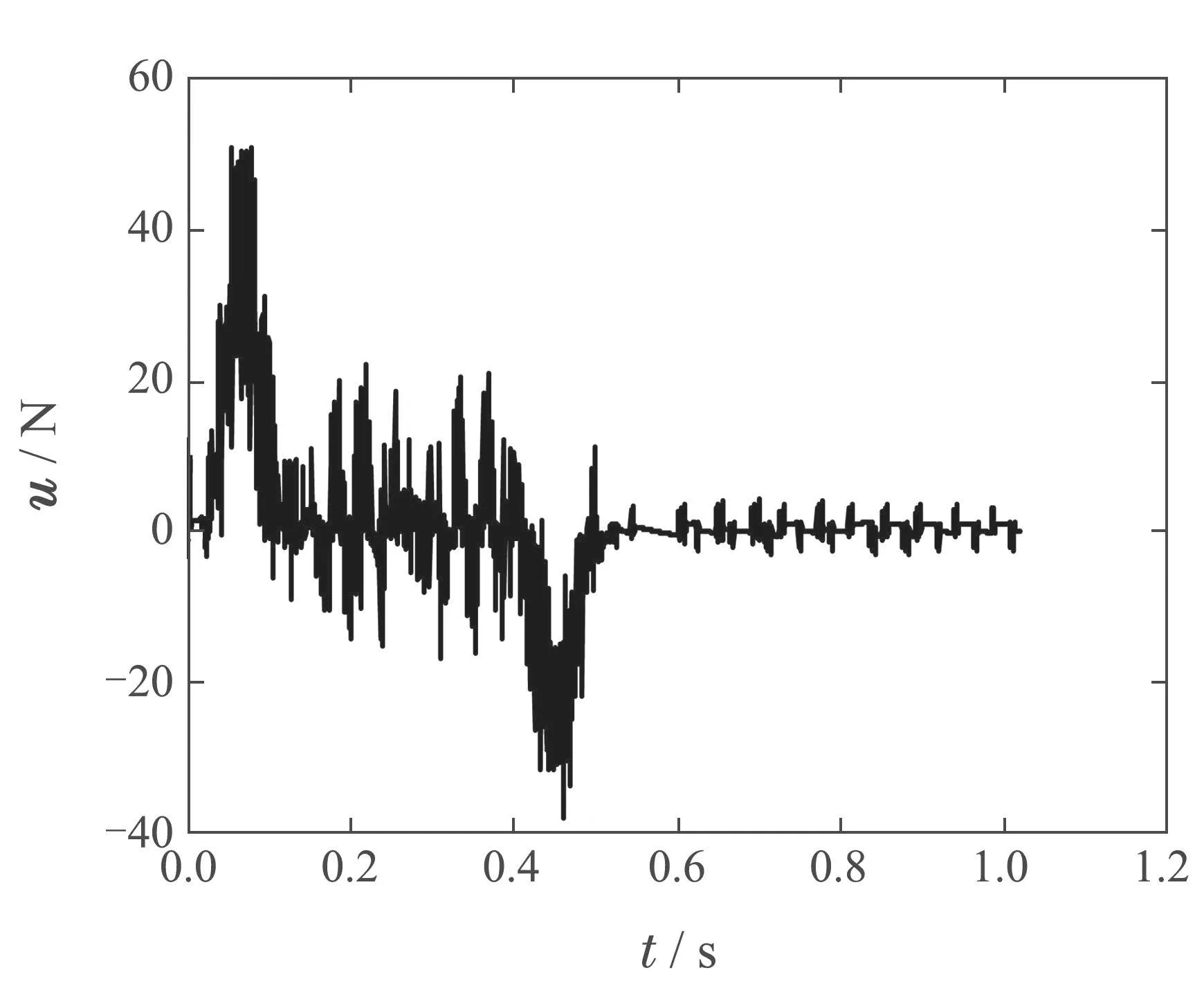
圖19 運(yùn)行軌跡1時(shí)的控制信號(hào)u曲線Fig.19 Control signal u curve when running trajectory 1

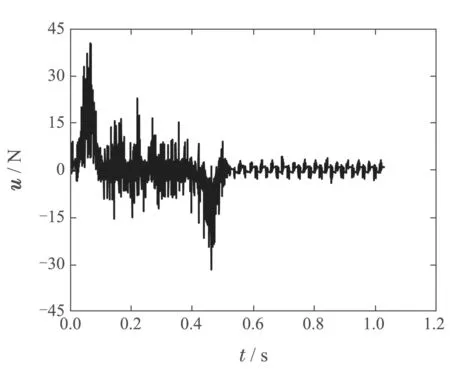
圖20 運(yùn)行軌跡2時(shí)的控制信號(hào)u曲線Fig.20 Control signal u curve when running trajectory 2

6 總結(jié)

為了實(shí)現(xiàn)在執(zhí)行器受約束情況下非重復(fù)性點(diǎn)到點(diǎn)軌跡的最優(yōu)跟蹤,本文提出了一種在執(zhí)行器約束情況下參數(shù)化輸入整形濾波器和前饋控制器的數(shù)據(jù)驅(qū)動(dòng)控制算法.算法運(yùn)用了數(shù)據(jù)驅(qū)動(dòng)的方法進(jìn)行迭代更新辨識(shí)最優(yōu)參數(shù),不依賴被控對(duì)象數(shù)學(xué)模型,并通過(guò)限制控制信號(hào)變化量和控制能量來(lái)達(dá)到對(duì)辨識(shí)參數(shù)的約束,從而滿足在執(zhí)行器約束條件下實(shí)現(xiàn)非重復(fù)性軌跡跟蹤,并且跟蹤誤差和辨識(shí)參數(shù)收斂到最優(yōu)值.通過(guò)仿真和實(shí)驗(yàn)驗(yàn)證: 本文算法能夠?qū)崿F(xiàn)在執(zhí)行器約束下對(duì)點(diǎn)到點(diǎn)軌跡的最優(yōu)跟蹤性能,并且對(duì)非重復(fù)性點(diǎn)到點(diǎn)軌跡具有一定的魯棒性.