華南師范大學(xué)數(shù)學(xué)科學(xué)院(510631) 葉秀錦

貴州省畢節(jié)市七星關(guān)區(qū)第五實(shí)驗(yàn)學(xué)校(551700) 臧軍

1 問(wèn)題背景

原題(《美國(guó)數(shù)學(xué)月刊》12214 題[1]) 設(shè)x,y,z是三角形ABC三條中線(xiàn)的長(zhǎng)度,三角形ABC的面積為S′.證明:

2 預(yù)備知識(shí)

引理1設(shè)D,E,F是三角形ABC三邊BC,AC,AB的中點(diǎn),三角形ABC的面積為S′,那么AD,BE,CF三邊的長(zhǎng)度可以構(gòu)成三角形,并且這個(gè)新三角形的面積為

證明如圖1 所示.連結(jié)AD,BE,CF,AD,BE,CF相交于I.延長(zhǎng)FE到G,使得EG=FE,連結(jié)AG,CG.連結(jié)DG交AC于H.

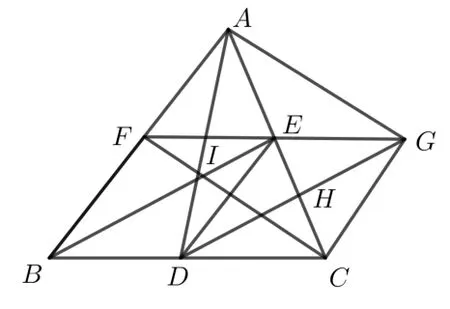
圖1

引理2已知a,b,c都是正數(shù),令p=a+b+c,q=ab+ac+bc,t=abc,那么有:(1)p2≥3q;(2)q2≥3pt;(3)pq≥9t;(4)p3≥27t;(5)p3-4pq+9t≥0.

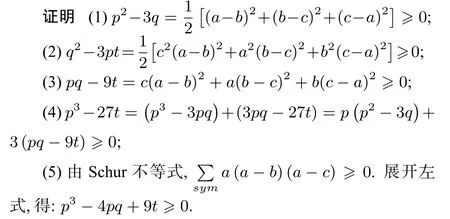
3 等價(jià)問(wèn)題與加強(qiáng)問(wèn)題

由引理1,可知x,y,z三邊的長(zhǎng)度可構(gòu)成一面積為S的三角形,S=不難將原問(wèn)題轉(zhuǎn)化為如下的等價(jià)命題:

4 命題2 的兩種證明

評(píng)注方法一通過(guò)代換轉(zhuǎn)化為三元對(duì)稱(chēng)不等式問(wèn)題,從而可以用上許多證明三元對(duì)稱(chēng)不等式的手段,是一種證明對(duì)稱(chēng)三角不等式的通法,易于證明比較強(qiáng)的結(jié)果,但對(duì)于證明一些比較弱的結(jié)果會(huì)顯得比較復(fù)雜.方法二由于Gerretsen不等式的局限性,不適用于證明一些較強(qiáng)的結(jié)果,但對(duì)于證明一些比較弱的結(jié)果會(huì)顯得比較方便.