一類含CFC-分數(shù)階導數(shù)微分方程的Lyapunov不等式及其解的存在唯一性

王楓, 葛琦

( 延邊大學 理學院, 吉林 延吉 133002 )

0 引言

1907年,Lyapunov[1]提出了下列邊值問題:

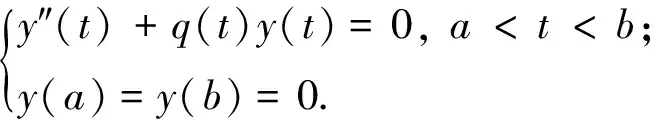
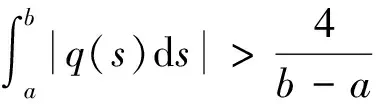
近年來,隨著分數(shù)階微分方程在各領域的廣泛應用,學者們又定義了許多不同的分數(shù)階導數(shù).例如:2018年,文獻[2]的作者研究了如下分數(shù)階微分方程的邊值問題:

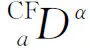
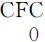
(1)

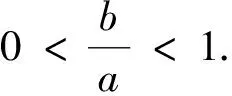
(2)

其中:u(t)是定義在[0,1]上的實值連續(xù)函數(shù).同時本文還將研究以下微分方程解的存在唯一性及其Hyers-Ulam穩(wěn)定性:

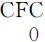
(3)

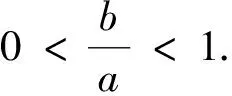
(4)

1 預備知識

定義1[7]定義函數(shù)f(t)∈L1([0,1],R)的s階黎曼劉維爾(Riemann-Liouville)分數(shù)階積分為:

其中s>0,τ>0, Γ(·)為Gamma函數(shù).

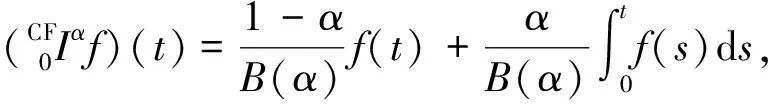
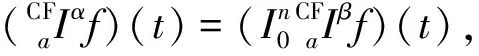
定義4[9]設函數(shù)f是定義在[0,1]上的實值函數(shù).定義函數(shù)f在左Caputo和Fabrizio意義下的α(α∈(0,1])階左Caputo分數(shù)階導數(shù)(簡稱CFC-分數(shù)階導數(shù))為

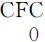
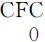
性質(zhì)1[9]設α∈(n,n+1],n≥1,u(t)是定義在[0,1]上的函數(shù),則有

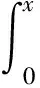
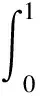
證明在式(1)兩邊同時作用CF0Ip后再利用性質(zhì)1和定義4可得:

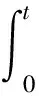
(5)

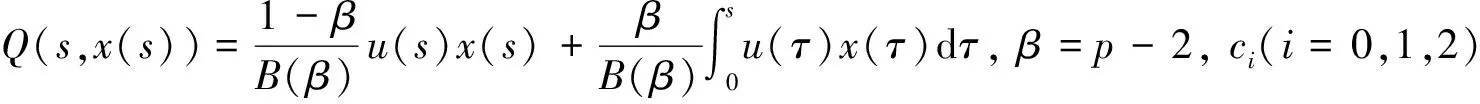
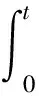
(6)

根據(jù)條件x′(0)= 0,對式(6)進行計算可得c1= 0.為了確定常數(shù)c2,計算下式:

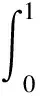
(7)

根據(jù)條件ax(1)+bx′(1)= 0,對式(7)進行計算可得:

即

(8)

將式(6)—(8)代入式(5)可得:

(9)

為了將式(9)整理成含有格林函數(shù)的形式,對其進一步計算得:

(10)

(11)

(12)

將式(10)—(12)代入式(9)可得:

x(t)=

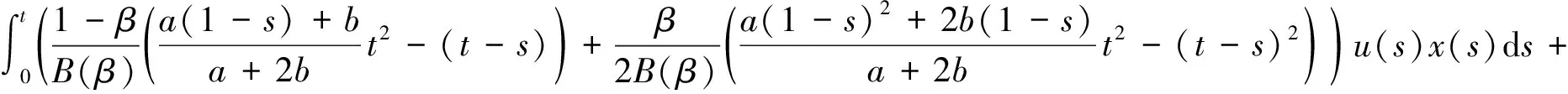
2 主要結論及其證明

引理3由引理1所定義的格林函數(shù)G(t,s)滿足如下不等式:

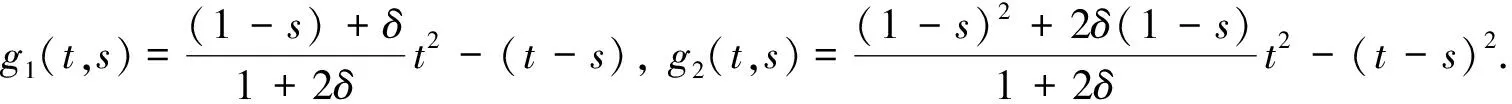
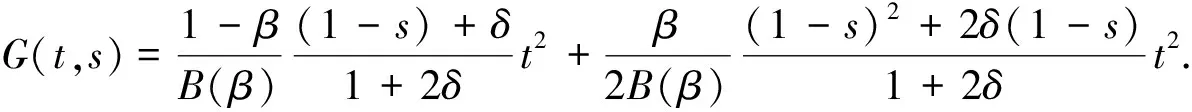
(13)

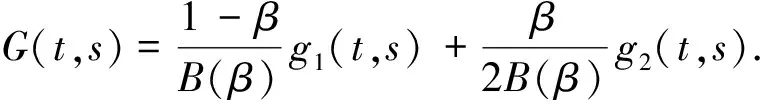
(14)

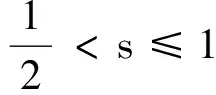
|g1(t,s)|≤g1(s,s).

(15)

由式(14)和式(15)可得,當0≤s≤1時,有:

(16)

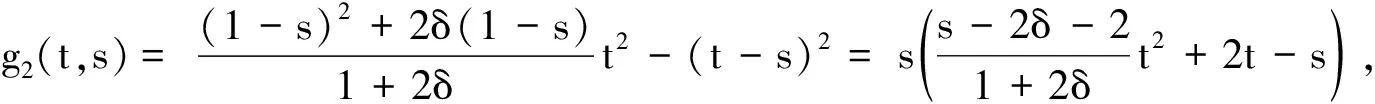
(17)

定理1若微分方程(1)和方程(2)存在非零解,則如下Lyapunov不等式成立:

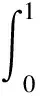
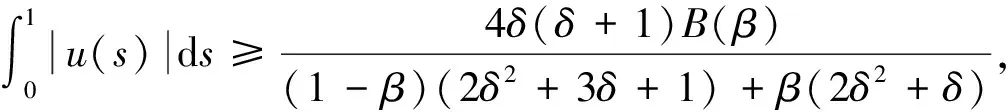
考慮如下特征值問題:

(18)

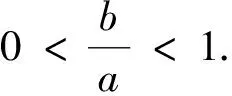
(19)

由推論1可知,如下推論2成立.

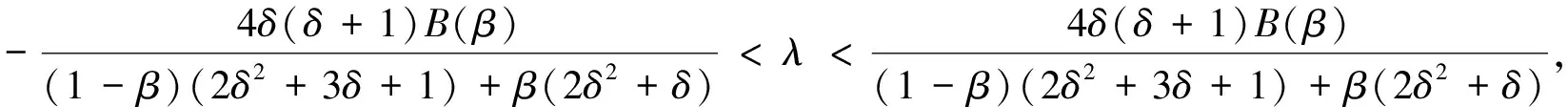
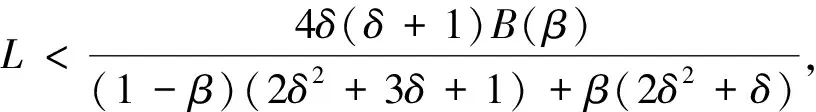
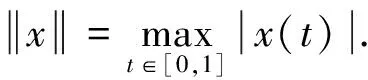
因此T為壓縮算子.再由Banach壓縮映像原理可知,存在不動點x*,使得Tx*=x*.由此可知,微分方程(3)和(4)存在唯一解,證畢.

下面考慮如下含CFC-分數(shù)階導數(shù)非線性微分方程解的Hyers-Ulam穩(wěn)定性:

(20)

其中f:[0,1]×R→R為連續(xù)函數(shù),且對任意的(t,x),(t,y)∈[0,1]×R存在常數(shù)L>0,使得|f(t,x)-f(t,y)|≤L|x-y|成立.

定理3非線性微分方程(20)的解是Hyers-Ulam穩(wěn)定的.

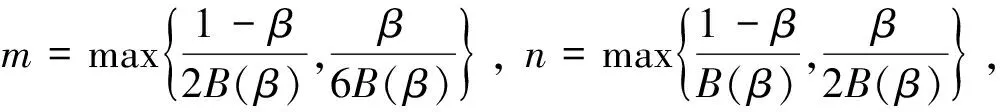
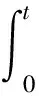
再由引理1可得:

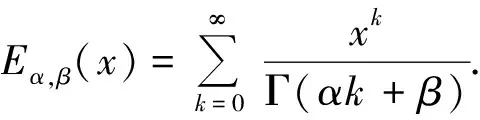
3 具體算例

考慮如下微分方程:

(21)

x(0)=x′(0), 2x(1)+x′(1)= 0,

(22)