泰勒展開式與超越不等式在高考中的應(yīng)用
王文琦
(江蘇省揚(yáng)州大學(xué)數(shù)學(xué)科學(xué)學(xué)院,江蘇 揚(yáng)州 225002)
筆者從泰勒公式基本形式出發(fā),證明了兩大超越不等式.筆者接著舉例分析了高考中以泰勒展開為背景的試題,并總結(jié)了高考中五大應(yīng)用題型,以期拋磚引玉.
1 泰勒展開式與超越不等式
1.1 泰勒公式形式

其中:f(n)(x0)表示f(x)在包含x0的某個(gè)閉區(qū)間[a,b]上具有n階導(dǎo)數(shù),等號(hào)后的多項(xiàng)式稱為函數(shù)f(x)在x0處的泰勒展開式,剩余的Rn(x)是泰勒公式的余項(xiàng),是(x-x0)n的高階無(wú)窮小量[1].
1.2 兩個(gè)超越不等式
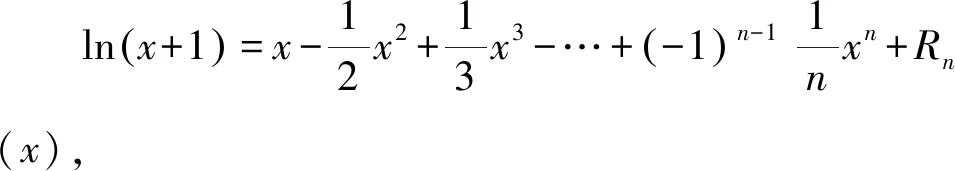
①
①中等號(hào)右邊只取第一項(xiàng),得
ln(x+1)≤x(x>-1).
②
用x-1替代②中的x,得lnx≤x-1(x>0).
③
④

證明因?yàn)?/p>
⑤
⑤式等號(hào)右邊取前兩項(xiàng),得ex≥x+1(x∈R).
⑥
用-x替代⑥式中的x,得e-x≥-x+1(x∈R).
⑦


2 舉例分析泰勒展開與高考題的聯(lián)系
2.1 一階導(dǎo)數(shù)放縮
例1 (2013年新課標(biāo)Ⅱ卷)已知函數(shù)f(x)=ex-ln(x+m),
(1)設(shè)x=0是f(x)的極值點(diǎn),求m,并討論f(x)的單調(diào)性;
(2)當(dāng)m≤2時(shí),證明f(x)>0.
命題手法分析第(2)問考查泰勒一階展開式:ex≥x+1>x-1≥lnx,所以可得ex-ln(x+2)>0,這就是第(2)問的命題背景.
2.2 二階導(dǎo)數(shù)放縮
例2 (2020年全國(guó)Ⅰ卷)已知函數(shù)f(x)=ex+ax2-x.
(1)當(dāng)a=1時(shí),討論f(x)的單調(diào)性;


這個(gè)式子使得x=2是一個(gè)極大值點(diǎn)(最大值點(diǎn)).但是,這樣構(gòu)造的導(dǎo)函數(shù)其原函數(shù)過于簡(jiǎn)單,不能滿足壓軸題的難度,那就增加一個(gè)分母[1]:


3 具體應(yīng)用
3.1 利用泰勒展開式證明不等式

證明設(shè)f(x)=ln(1+x)(-1 則f(x)在x=0處有泰勒公式 例2已知x=0是函數(shù)f(x)=x(ax-tanx)的極大值點(diǎn),則a的取值范圍是( ). A.(-∞,0] B.(-∞,1] C.[0,+∞) D.[1,+∞) 解析x=0是函數(shù)f(x)=x(ax-tanx)的極大值點(diǎn),等價(jià)于x=0是函數(shù)g(x)=x(axcosx-sinx)的極大值點(diǎn).由f(x)在x=0的泰勒展開為 A.a 例4 已知函數(shù)f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求實(shí)數(shù)k的取值范圍; 當(dāng)0 例5 已知函數(shù)f(x)=ex-e-x-2x, (1)設(shè)g(x)=f(2x)-4bf(x),當(dāng)x>0時(shí),g(x)>0,求b的最大值; 解析(1)函數(shù)g(x)=f(2x)-4bf(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,求導(dǎo)得 g′(x)=2(ex+e-x-2)(ex+e-x+2-2b). ①由ex+e-x>2,則ex+e-x+2>4.當(dāng)2b≤4,即b≤2時(shí),g′(x)≥0,當(dāng)且僅當(dāng)x=0時(shí)取等號(hào). 從而g(x)在R上為增函數(shù),而g(0)=0,所以x>0時(shí),g(x)>0,符合題意. ②當(dāng)b>2時(shí),若x滿足2 綜合①②知,b≤2,即b的最大值為2. 所以ln2的近似值為0.693. 總結(jié)泰勒公式是高等數(shù)學(xué)中的重要知識(shí),它構(gòu)成了眾多高考數(shù)學(xué)題中的命題背景.所以知道常見函數(shù)的泰勒展開式,就能捕捉到試題背后蘊(yùn)藏的不等式,應(yīng)用時(shí)用初等數(shù)學(xué)的方法證明即可.在高中數(shù)學(xué)學(xué)習(xí)的過程中適當(dāng)擴(kuò)展與了解一些高等數(shù)學(xué)的知識(shí),對(duì)于高中生尤其是優(yōu)等生是必要的.

3.2 泰勒展開式與函數(shù)的極值界定


3.3 利用超越不等式比較大小


3.4 利用對(duì)數(shù)型超越放縮證明不等式






3.5 利用指數(shù)型超越放縮證明不等式








