廣東省云浮市云浮中學(xué)(527300)成永深

題目(《數(shù)學(xué)教學(xué)》2023 年第2 期問題1173 為) 當(dāng)x> 1,y> 2,z> 3 時(shí), 求的最小值.

二變式拓展

2.1 變式1當(dāng)x>1,y>2 時(shí),求

的最小值.

解如圖1 所示, 在直線l上依次取點(diǎn)P,O,Q, 使得OP= 1,OQ= 2,AP垂直于PQ且OA=x,BQ垂直于PQ且OB=y, 四邊形APQA′為矩形.則所以

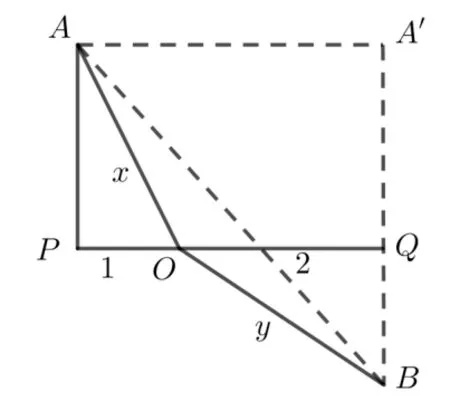
圖1

取等條件為A,O,B三點(diǎn)共線且A′B= 3, 即y=2x,√即時(shí)取等號(hào).

變式2當(dāng)x>1,y>2,z>4 時(shí),求

的最小值.

解設(shè)a,b,c>0,由代數(shù)變形結(jié)合均值不等式得

2.2 推廣

當(dāng)a1=a+1,a2=b+2,b1= 1,b2= 2 時(shí),則問題就是2018 奧地利數(shù)學(xué)奧林匹克不等式題:

已知a,b∈R+,則

推廣2已知a1>b1,a2>b2,··· ,an>bn且a1,a2,··· ,an為變量,{bn}為正項(xiàng)等差數(shù)列或等比數(shù)列, 記數(shù)列{bn}的前n項(xiàng)和為sn,則

的最小值為2sn.

2.3 幾個(gè)結(jié)論

該問題便是2018 奧地利數(shù)學(xué)奧林匹克不等式題的推廣.