一類離散廣義非線性 Schr?d inger系統(tǒng)周期解的存在性

譚偉明,覃學(xué)文

(梧州學(xué)院數(shù)理系,中國 梧州 543002)

一類離散廣義非線性 Schr?d inger系統(tǒng)周期解的存在性

譚偉明,覃學(xué)文＊①

(梧州學(xué)院數(shù)理系,中國 梧州 543002)

把一些文獻討論的離散廣義非線性 Schr?dinger方程推廣到了n維空間,應(yīng)用臨界點理論,得到了一類離散廣義非線性 Schr?dinger系統(tǒng)存在多個非零周期解的充分條件.

Schr?dinger系統(tǒng) ;臨界點 ;周期解

非線性 Schr?dinger方程是現(xiàn)代物理和數(shù)學(xué)理論研究中的一個基本方程,對這個方程的研究在推動現(xiàn)代物理和數(shù)學(xué)的發(fā)展起著非常重要的作用.從數(shù)學(xué)家的觀點來看,非線性 Schr?dinger方程也具有極大的吸引力,數(shù)學(xué)家們對這個方程關(guān)注和探討的問題也是多方面的.近十多年來,許多學(xué)者對非線性 Schr?dinger方程及其應(yīng)用作了深入的研究,取得了一定的成果[1-9].

文 [4]從離散非線性 Schr?dinger方程

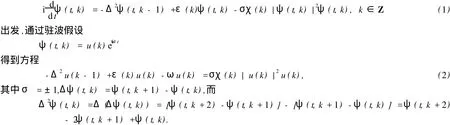
1 預(yù)備知識和變分結(jié)構(gòu)

2 主要結(jié)果

下面證明系統(tǒng)(6)還有其它的非零T-周期解,為此只需證明泛函J(X)在ET上還有其它的非零臨界點.應(yīng)用山路引理證明.

可證明泛函J滿足環(huán)繞定理的條件.由于已證明泛函J滿足 P-S條件,因此只需證明泛函J滿足環(huán)繞定理的條件(1)和(2).

即轉(zhuǎn)化為(1)的情形,由上述討論可知,泛函 -J至少有 2個臨界點,從而泛函J至少有 2個非零臨界點,于是系統(tǒng)(6)至少存在 2個非零T-周期解.

[1]BEREZ IN F A,SHUB IN M A.The Schr?dinger equation[M].Netherlands:KluwerAcademic Publishers,2002.

[2]ABLOW ITZM J,PR INAR IB,TRUBATCH A D.Diserete and continuous nonlinear Schr?dinger systems[M].New York:Cambridge University Press,2004.

[3]MULLER-KI RSTEN H JW.Introduction to quantum mechanics:Schr?dinger equation and path integral[M].Singapore:World Scientific Printers(S)Pte Ltd,2006.

[4]PANKOV A.Gap solitons in periodic discrete nonlinear Schr?dinger equation[J].Nonlinearty,2006,19:27-40.

[5]ALEXANDRU D IONESCU,CARLOS E KEN IG.Uniqueness properties of solutions of Schr?dinger equations[J].Journal of FunctionalAnalysis,2006,232:90-136.

[6]ALOMAR IA K,NOORAN IM SM,NAZAR R.Explicit series solutionsof some linear and nonlinear Schr?dinger equations via the homotopy analysismethod[J].Communications in Nonlinear Science and Numerical Simulation,2009,14:1 196-1 207.

[7]G IOVANNA CERAM I,R ICCARDO MOLLE.Positive solutions for some Schr?dinger equations having partially periodic potentials[J].Journal ofMathematicalAnalysis and Applications,2009,359:15-27.

[8]NAKAO HAYASH I,PAVEL INAUMK IN.Asymptotics of odd solutionsof quadratic nonlinear Schr?dinger equations[J].Journal ofMathematicalAnalysis and Applications,2009,359:146-158.

[9]KOPYLOVA E A.On the asymptotic stability of solitarywaves in the discrete Schr?dinger equation coupled to a nonlinear oscillator[J].NonlinearAnalysis,2009,71:3 031-3 046.

Existence Periodic Solution of the Generalized D iscrete Nonlinear Schr?dinger System

TAN W ei-m ing,Q IN Xue-wen
(School ofMathematics and Physics,Wuzhou University,Wuzhou 543002,China)

The generalized discrete nonlinear Schr?dinger equation discussed in some literature are extented ton-d imensional space.Using critical point theory,some sufficient conditions are obtained for the existence periodic solution of the generalized discrete nonlinear Schr?dinger system.

Schr?dinger systems;critical point theory;periodic solution

O413.1

A

1000-2537(2010)04-0046-07

2010-05-17

梧州學(xué)院科研基金資助項目 (2009B012);廣西教育廳科研基金資助項目(2008MS121);廣西自然科學(xué)基金資助項目 (桂科自 0991279)

＊通信作者,E-mail:hnsyb@126.com

(編輯 陳笑梅)