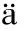三元多項式代數(shù)上的 Z2-分次自同構(gòu)

孫 曉 松

(吉林大學(xué) 數(shù)學(xué)學(xué)院, 長春 130012)

設(shè)K是特征零的域,φ是多項式代數(shù)K[x1,…,xn]上的自同態(tài), 記φ=(φ1,…,φn), 其中φi=φ(xi)(i=1,2,…,n). 形如(x1,…,xi-1,cxi+a,xi+1,…,xn)的自同構(gòu)稱為初等自同構(gòu), 其中: 0≠c∈K;a不含xi. 有限個初等自同構(gòu)的復(fù)合稱為tame自同構(gòu). “K[x1,…,xn]上的自同構(gòu)是否都是tame的”稱為tame生成子問題[1-2]. 2維tame生成子問題成立[1]. 穩(wěn)定xi的自同構(gòu)稱為xi-自同構(gòu), 有限個xi-初等自同構(gòu)的復(fù)合稱為xi-tame自同構(gòu). 下面用K[x,y,z]表示3元多項式代數(shù). Nagata[3]構(gòu)造了自同構(gòu):σ=(x-2(xz+y2)y-(xz+y2)2z,y+(xz+y2)z,z), 發(fā)現(xiàn)σ不是z-tame的, 并猜想它不是tame的. Shestakov等[4-5]證實了Nagata的猜想, 證明了若一個z-自同構(gòu)不是z-tame的, 則它不是tame的. 文獻(xiàn)[6]證明了σ1,σ2均為非tame坐標(biāo). 文獻(xiàn)[7]證明了存在線性自同構(gòu)L使得Lσ可線性化. 文獻(xiàn)[8]證明了K[x,y,z]上非tame的z-自同構(gòu)不能提升為自由結(jié)合代數(shù)上的z-自同構(gòu).

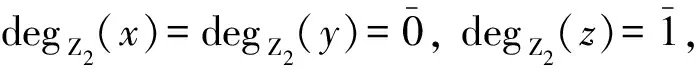
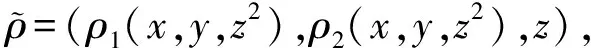
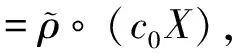
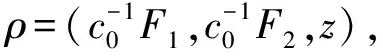
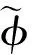
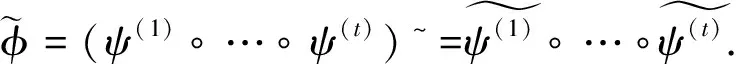
定理2設(shè)φ是K[x,y,z]上的一個分次自同構(gòu), 若φ為tame自同構(gòu), 則φ必為分次tame自同構(gòu).

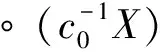
φ(x)=(ψ°E-1)(x)=ψ(x-f0-f1)=x+g0+g1-f0(y+h0,z)-f1(y+h0,z).

由φ(x)∈R0知,g1=f1(y+h0,z). 令ψ′=(x+g0,y+h0,z),E′=(x-f0,y,z), 則有

ψ′°E′=(x+g0,y+h0,z)°(x-f0,y,z)=(x+g0-f0(y+h0,z),y+h0,z)=φ.

注意E′是分次初等自同構(gòu),ψ′是分次自同構(gòu), 且tdegψ′≤tdegψ

[2] Bass H. Automorphisms of Polynomial Rings [J]. Abelian Group Theory: Lecture Notes in Math 1006 [M]. Berlin: Springer, 1983: 762-771.

[3] Nagata M. On the Automorphism Group ofk[X,Y]: Lectures in Math 5 [M]. Tokyo: Kyoto University, 1972.

[4] Shestakov I P, Umirbaev U U. Poisson Brackets and Two-Generated Subalgebras of Rings of Polynomials [J]. J Amer Math Soc, 2004, 17(1): 181-196.

[5] Shestakov I P, Umirbaev U U. The Tame and the Wild Automorphisms of Polynomial Rings in Three Variables [J]. J Amer Math Soc, 2004, 17(1): 197-227.

[6] Umirbaev U U, YU Jie-tai. The Strong Nagata Conjecture [J]. Proc Natl Acad Sci USA, 2004, 101(13): 4352-4355.

[7] Maubach S, Poloni P M. The Nagata Automorphism Is Shifted Linearizable [J]. J Algebra, 2009, 321(3): 879-889.

[8] Belov-Kanel A, YU Jie-tai. On the Lifting of the Nagata Automorphism [J]. Sel Math New Ser, 2011, 17: 935-945.