張 瑩

(沈陽大學(xué)師范學(xué)院,遼寧沈陽 110044)

一類不確定T-S模糊系統(tǒng)的H∞控制器設(shè)計

張 瑩

(沈陽大學(xué)師范學(xué)院,遼寧沈陽 110044)

基于線性矩陣不等式的方法,研究了一類帶有不確定參數(shù)的T-S模糊系統(tǒng)的H∞控制器設(shè)計問題.給出了參數(shù)不確定的T-S模糊系統(tǒng)的系統(tǒng)建模以及系統(tǒng)的二次穩(wěn)定性,并且對此類T-S模糊系統(tǒng)的H∞控制問題進行了探討,給出了新的基于狀態(tài)反饋H∞控制器的設(shè)計方法.

線性矩陣不等式(LMIs);T S模糊系統(tǒng);二次穩(wěn)定;H∞控制;狀態(tài)反饋

T S模糊系統(tǒng)模型是在局部線性模型的基礎(chǔ)上通過隸屬函數(shù)得到的非線性模型,由“如果—則”規(guī)則描述,可以通過模糊規(guī)則給出非線性系統(tǒng)的局部線性表出,因此,借助線性系統(tǒng)的理論和方法,很多學(xué)者對T-S模糊系統(tǒng)進行了分析和研究[111],其中多數(shù)研究的T-S模糊系統(tǒng)模型中,每個子系統(tǒng)的系數(shù)矩陣是確定的.而本文給出的T-S模糊系統(tǒng),則是系數(shù)矩陣帶有實參數(shù)的不確定系統(tǒng).

1 一類參數(shù)不確定的T-S模糊系統(tǒng)

本文給出如下帶有實參數(shù)的T-S模糊模型所描述的非線性系統(tǒng).

系統(tǒng)的模糊規(guī)則k:若ω1(t)是Fk1,ω2(t)是Fk2,…,ωn(t)是Fkn,則

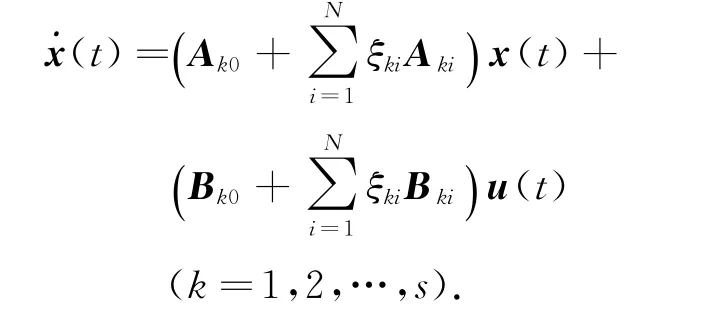
式中,Fkj是模糊集;ω(t)=[ω1(t),ω2(t),…, ωn(t)]T是可測系統(tǒng)變量,是前件變量;x(t)∈Rn是狀態(tài)變量;u(t)∈Rm是控制輸入變量;s為模糊規(guī)則數(shù);ξki(k=1,2,…,s;i=1,2,…,N)是不確定的實參數(shù),且滿足0≤ξki≤α,α為給定的正數(shù); Aki,Bki(k=1,2,…,s;i=0,1,…,N)是系數(shù)矩陣.

模糊系統(tǒng)的整個狀態(tài)方程為

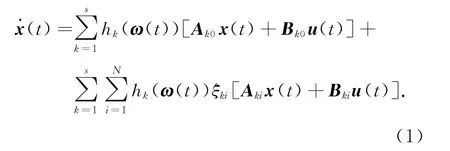
式中,

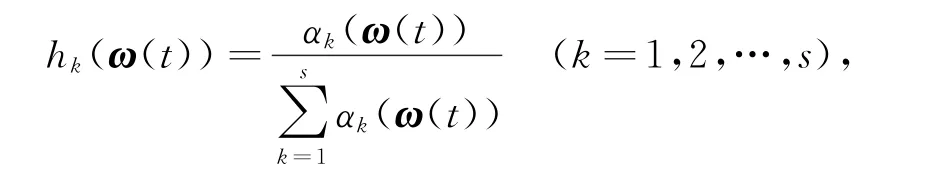
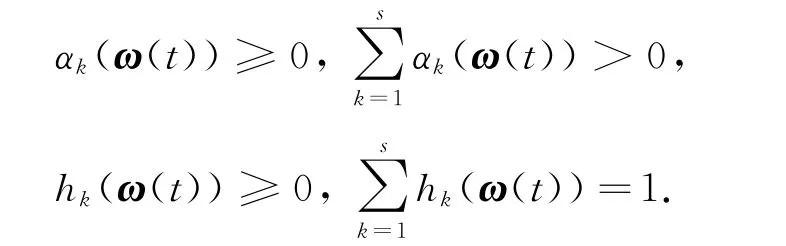
對于不確定模糊系統(tǒng)(1),當(dāng)控制輸入變量為0時,如果存在正數(shù)d和一個正定矩陣X,對于V(x(t))=x(t)TXx(t),有˙V(x(t))≤ -d x(t)Tx(t)成立,則T-S模糊系統(tǒng)(1)被稱為二次穩(wěn)定[12]的.

引理[12]若存在正定對稱矩陣P,使得下式成立:

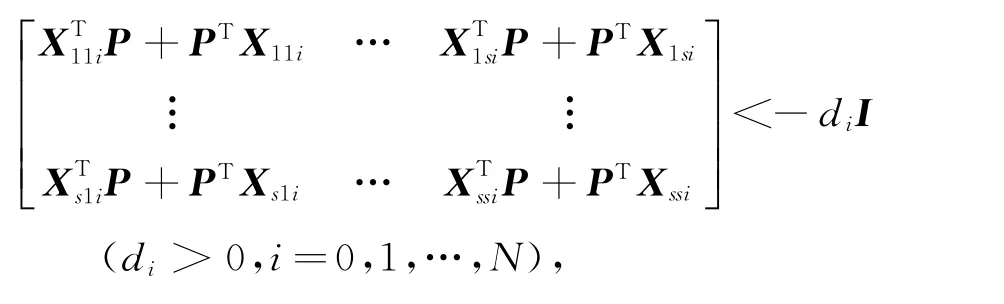
則存在狀態(tài)反饋控制器

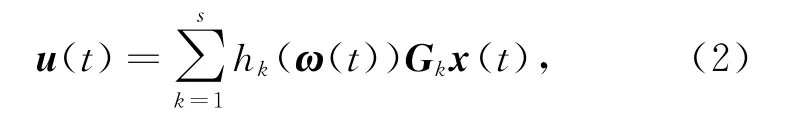
使得閉環(huán)系統(tǒng)

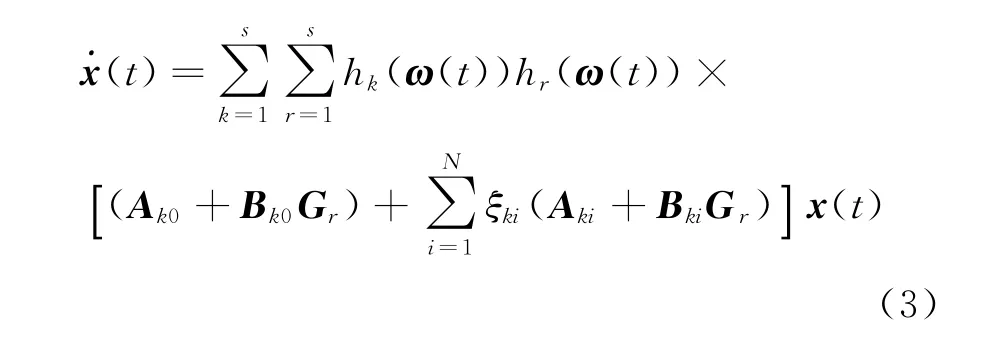
當(dāng)控制輸入變量為零時是二次穩(wěn)定的.其中

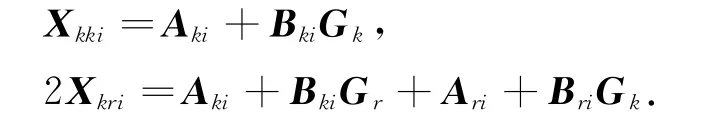
2 不確定T-S模糊系統(tǒng)的H∞控制器設(shè)計

由二次穩(wěn)定性,研究如下帶有實參數(shù)的不確定模糊系統(tǒng):

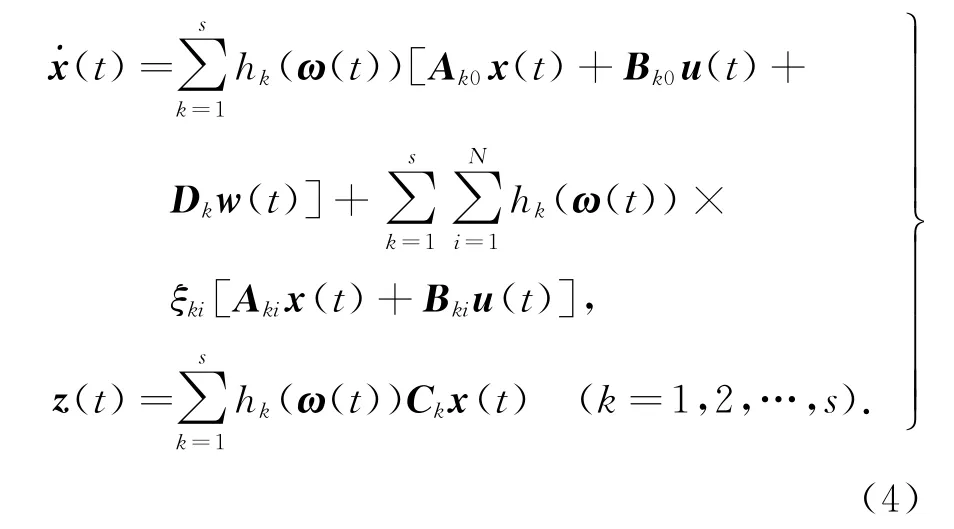
對于T-S模糊系統(tǒng)(4),設(shè)計狀態(tài)反饋控制器(2),使得當(dāng)w(t)≡0時,閉環(huán)系統(tǒng)是二次穩(wěn)定的;且在零初始條件下,對于給定的正數(shù)γ,對于任意的外界干擾輸入w(t)∈L2[0,+∞),控制輸出z(t)滿足‖z(t)‖2≤d‖w(t)‖2.其中,0＜為L2范

式中,w(t)∈Rq是平方可積的干擾輸入變量;Ck, Dk(k=1,2,…,s)是適當(dāng)維數(shù)的常數(shù)矩陣;z(t)∈Rp是控制輸出變量.數(shù).

此時稱T-S模糊系統(tǒng)(4)的H∞范數(shù)小于γ.

定理 對于給定的正數(shù)γ,如果存在矩陣Gr(r=1,2,…,s)和對稱正定矩陣P,使得下式成立:

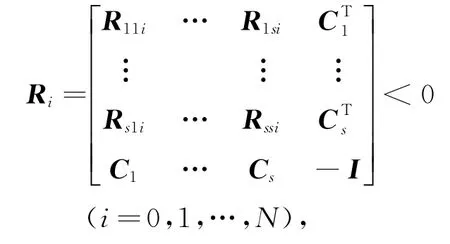
則對于系統(tǒng)(4),狀態(tài)反饋(2)產(chǎn)生的如下閉環(huán)系統(tǒng)的H∞范數(shù)小于γ:

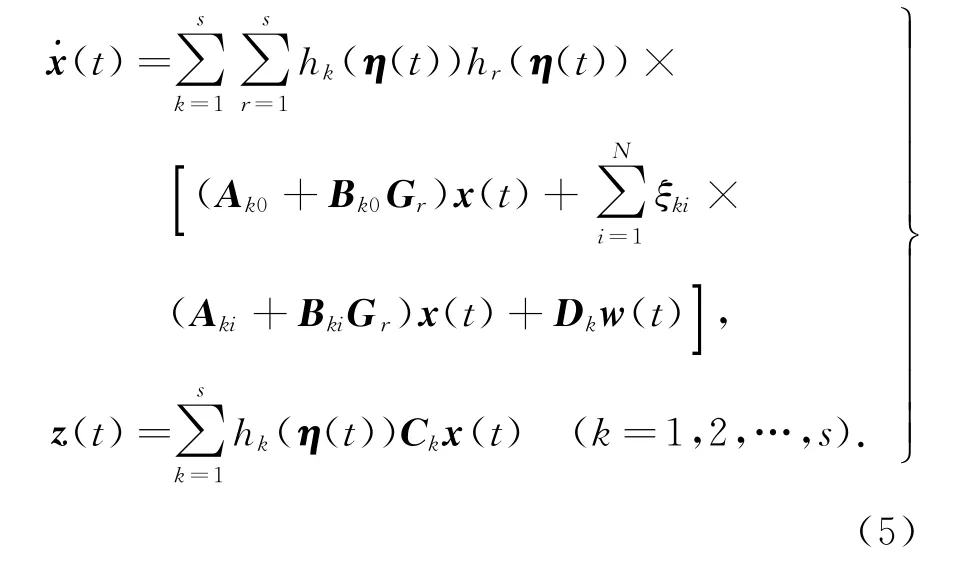
式中,

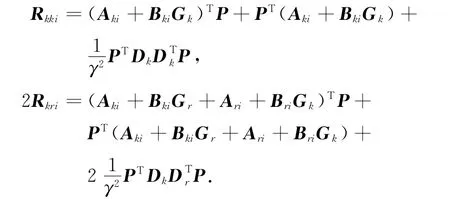
證明 設(shè)Xkki=Aki+BkiGk,2Xkri=Aki+ BkiGr+Ari+BriGk.

先證當(dāng)w(t)≡0時,閉環(huán)系統(tǒng)是二次穩(wěn)定的.

由引理和Schur補公式,容易得到

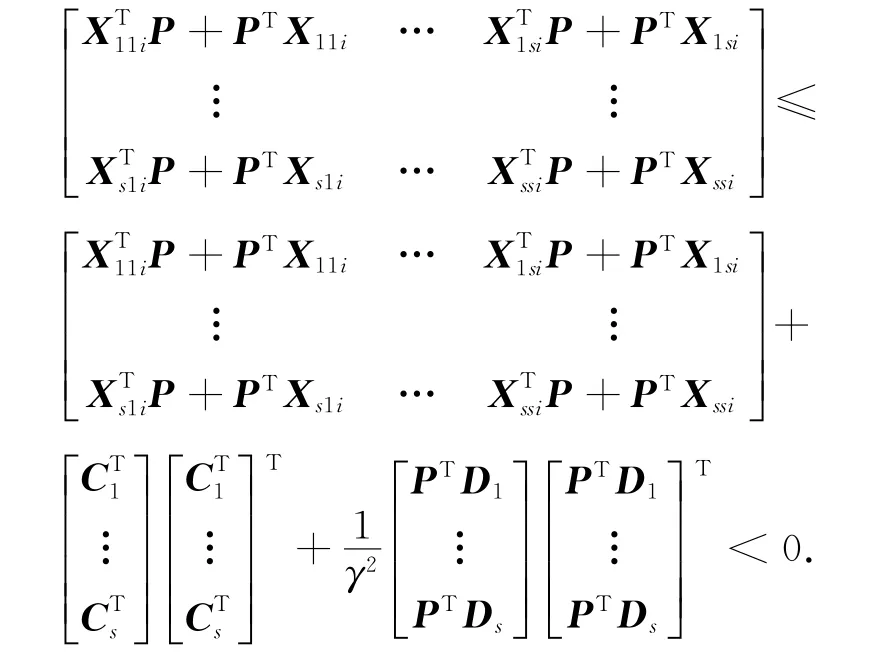
令V(x(t))=xTPx,則

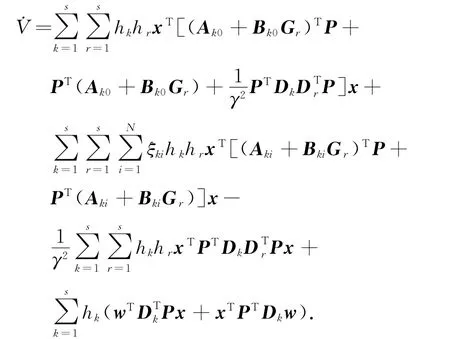
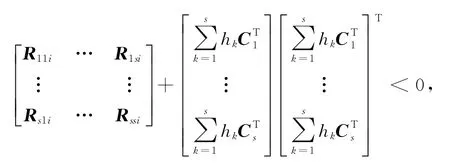
所以

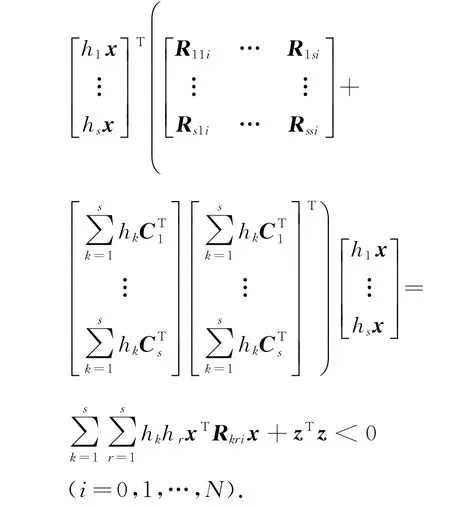
因為存在正數(shù)di＞0(i=0,1,…,N),使得

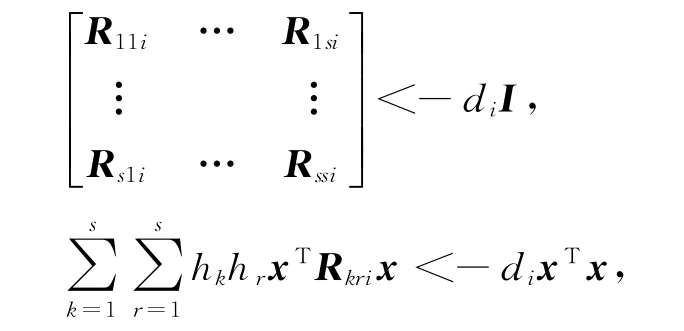
所以

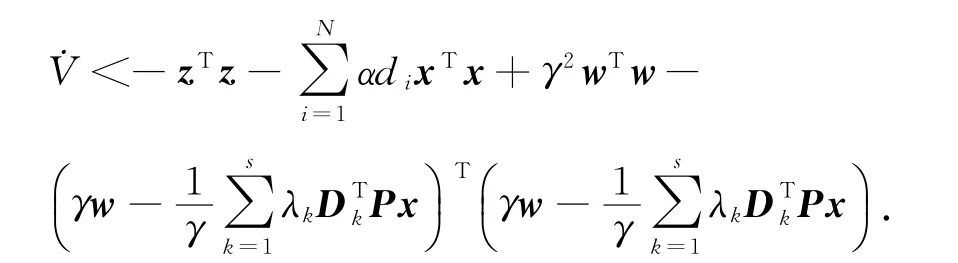
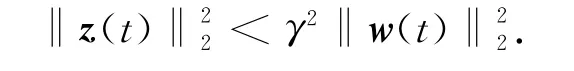
由x(0)=0,則V(x(0))=0.上式兩端對t從0到+∞積分,得推論 對于給定的正數(shù)γ,若存在正定對稱矩陣Q及矩陣Er(r=1,2,…,s),使得下式成立:

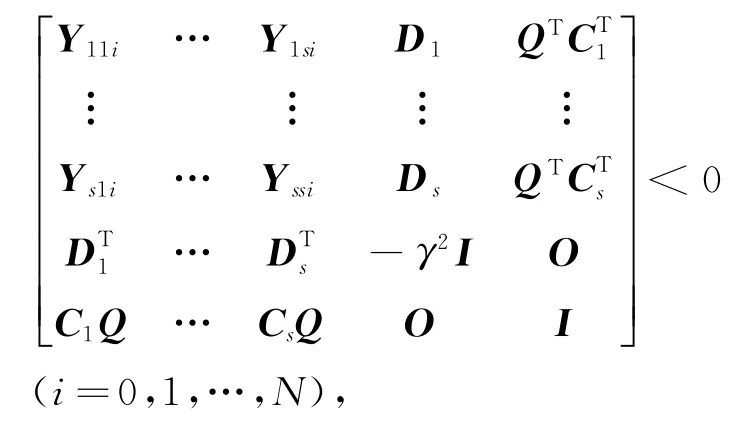
則狀態(tài)反饋(2)產(chǎn)生的閉環(huán)系統(tǒng)(5)的H∞范數(shù)小于γ,且Gr=ErQ-1(r=1,2,…,s).其中

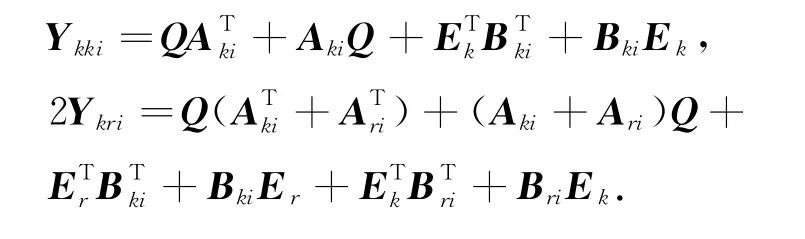
3 結(jié) 語

本文主要針對帶有實參數(shù)的一類不確定T-S模糊系統(tǒng),給出了系統(tǒng)的模型,不確定性體現(xiàn)在模糊系統(tǒng)的狀態(tài)方程系數(shù)矩陣中帶有實參數(shù).由系統(tǒng)的二次穩(wěn)定性,對系統(tǒng)的基于狀態(tài)反饋的H∞控制問題進行了研究,應(yīng)用線性矩陣不等式(LMIs)給出了一個新的狀態(tài)反饋H∞控制器的設(shè)計方法.

[1]Tanaka K,Sugeno M.Stability Analysis and Design of Fuzzy Control Systems[J].Fuzzy Sets and Systems, 1992,45(2):135-156.

[2]Feng G,Cao G,Rees W.An Approach to H∞Control of a Class of Nonlinear Systems[J].Automatic,1996,32 (10):1469 1474.

[3]Tanaka K,Ikeda T,Wang H O.Robust Stabilization of a Class of Uncertain Nonlinear Systems via Fuzzy Control: Quadratic Stabilizability,H∞Control Theory,and Linear Matrix Inequalities[J].IEEE Transactions on Fuzzy Systems,1996,4(1):1 13.

[4]Cao S G,Rees N W,Feng G.H∞Control of Nonlinear Continuous Time Systems Based on Dynamical Fuzzy Models[J].International Journal of Systems Science, 1996,27(9):821-830.

[5]Yakubovich V A.The S-procedure in Nonlinear Control Theory[J].Vestnik Leningrad University:Mathematics, 1977(4):73-93.

[6]佟紹成,王濤,王艷平,等.模糊控制系統(tǒng)的設(shè)計及穩(wěn)定性分析[M].北京:科學(xué)出版社,2004:15-32.

(Tong Shaocheng,Wang Tao,Wang Yanping,et al.The Design and Stability Analysis of Fuzzy Control System [M].Beijing:Science Press,2004:15 32.)

[7]Lee K R,Jeung E T,Park H B.Robust Fuzzy H∞Control for Uncertain Nonlinear Systems via State Feedback:An LMI Approach[J].Fuzzy Sets and Systems,2001,120 (1):123-134.

[8]Zhang J M,Li R H,Zhang P A.Stability Analysis and Systematic Design of Fuzzy Control Systems[J].Fuzzy Sets and Systems,2001,20(1):65 72.

[9]Liu X D,Zhang Q L.New Approaches to H∞Controller Designs Based on the Fuzzy Observers for T-S Fuzzy Systems via LMI[J].Automatic,2003,39(9):1571-1582.

[10]Liu X D,Zhang Q L.Approaches to Quadratic Stability Conditions and H∞Control Designs for T-S FuzzySystems[J].IEEE Transactions on Fuzzy Systems,2003, 11(3):830 839.

[11]Zhang Ying,WangYanan.Quadratic Stability and H∞Control of a Class of Uncertainty T-S Fuzzy Systems[C]∥23rd Chinese Control and Decision Conference(CCDC 2011).Mianyang,2011:3493 3496.

[12]Zhai Ding,Zhang Ying.Robust H∞Controller Design for Uncertainty Fuzzy Systems[C]∥21st Chinese Control and Decision Conference(CCDC 2009).Guilin, 2009:4143-4146.

H∞Control of T-S Fuzzy Systems with Real Parametric Uncertainty

Zhang Ying
(Normal School,Shenyang University,Shenyang 110044,China)

Based on linear matrix inequalities(LMIs),the problem of H∞control of a class of T-S fuzzy systems with real parametric uncertainty is studied.The model of the T-S fuzzy systems is given,as well as the conditions for quadratic stability.The conditions for H∞control are studied,and the new designing method of the state feedback H∞controller is presented.

linear matrix inequalities(LMIs);T-S fuzzy systems;quadratic stability;H∞control; state feedback

TP 13

A

【責(zé)任編輯:王 穎】

2095-5456(2014)02-0169-04

2014-01-02

張瑩(1973-),女,吉林長春人,沈陽大學(xué)講師.