不完全信息下兩個內(nèi)部交易者的交易行為分析
鞏馥洲, 尚宏媛
(1.中國科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院,北京 100190;2.北京科技大學(xué)數(shù)理學(xué)院,北京 100083)
不完全信息下兩個內(nèi)部交易者的交易行為分析
鞏馥洲1, 尚宏媛2
(1.中國科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院,北京 100190;2.北京科技大學(xué)數(shù)理學(xué)院,北京 100083)
當(dāng)市場上存在兩個擁有不完全信息的內(nèi)部交易者時,研究了其對待風(fēng)險的態(tài)度分別為風(fēng)險喜好、風(fēng)險中性與風(fēng)險厭惡情況下模型在混合策略空間中離散時間的均衡解和高頻交易下均衡的漸近行為特征,并分析了相關(guān)模型的經(jīng)濟金融學(xué)意義.
不完全信息;內(nèi)部交易;混合策略均衡;高頻交易;漸近分析
1 前言
許多關(guān)于內(nèi)部交易的研究都是在文獻[1]基礎(chǔ)上對內(nèi)部交易者交易策略的研究,分析內(nèi)部交易者如何選擇交易策略以使其利用私有信息所獲得的利潤達到最大.文獻[1]從一次交易的單期模型入手,討論了多期交易的序貫?zāi)P秃瓦B續(xù)時間模型.文獻[2]發(fā)現(xiàn)文獻[1]模型在設(shè)定中存在矛盾.他們基于文獻[1]模型重新考慮當(dāng)期內(nèi)部交易者策略對定價規(guī)則的影響,給出了風(fēng)險喜好型,風(fēng)險中性型,風(fēng)險厭惡型三個替代模型的多期離散均衡,并用漸近分析方法對三個模型的離散結(jié)果進行了漸近分析,得到了在高頻交易情況下均衡的漸近行為特征.基于對文獻[3]的改進,文獻[4]和文獻[5]研究了混合策略空間中兩個內(nèi)部交易者的多期離散均衡,用漸近分析方法對高頻交易情況下的均衡特征進行了分析,由此獲得了相關(guān)的經(jīng)濟金融意義.文獻[6]或文獻[7]在純策略空間中研究了一個內(nèi)部交易者知道風(fēng)險資產(chǎn)部分信息的交易行為.本文基于文獻[6]或文獻[7]的模型,研究了兩個擁有不完全信息的內(nèi)部交易者在混合策略空間中的多期離散均衡及其高頻交易下的行為特征,并分析其經(jīng)濟金融意義.
2 預(yù)備知識
假設(shè)市場上存在一種可交易資產(chǎn),其清算價值為ν,且正態(tài)隨機變量ν~N(p0,).考慮時間段[0,1]上的交易,設(shè)交易起始時刻為t=0,交易結(jié)束時刻為t=1,市場中總共進行了N次交易,第n次交易發(fā)生時刻記為tn.假設(shè)0=t0 (1)不完全信息內(nèi)部交易者:此類內(nèi)部交易者沒有獲得交易風(fēng)險資產(chǎn)真實價值ν的完全信息,而是僅知道ν+ε的值,且ν與ε獨立,其中正態(tài)隨機變量ε~N(0,).設(shè)xin為第i個內(nèi)部交易者在第n期的交易量,pn為第n期交易時資產(chǎn)的價格,則在第n?1期交易之后與第n期交易之前,第i個該類交易者擁有的信息為: 即xi1,···,xi,n?1;p1,···,pn?1,ν+ε生成的σ-代數(shù).第i個該類交易者根據(jù)ν+ε及p1,···,pn?1對未來預(yù)期收益總和按其對待風(fēng)險的態(tài)度進行最優(yōu)化,即選擇xin,···,xiN,按第i個交易者對待風(fēng)險的態(tài)度,使的對應(yīng)物最大,其中第k期收益為πik(xik,pk)=(ν?pk)xik. (2)噪聲交易者:該類交易者只是隨機地進行交易,不進行任何最優(yōu)化決策.設(shè)μn為噪聲交易者第n期的交易量,它們獨立同分布,且都為正態(tài)隨機變量,即μn~N(0,?tN). (3)做市商:做市商每次都能觀察到總的訂單流,第n期觀察到的交易量為: 所以,在第n?1期交易之后與第n期交易之前,做市商的信息集為σ(y1,···,yn?1;p1,···,pn?1),即y1,···,yn?1;p1,···,pn?1生成的σ-代數(shù).做市商在第n期利用前n期總交易量對標(biāo)的資產(chǎn)真實價格進行最優(yōu)預(yù)測,使用定價權(quán)利保持市場的有效性,pn=E(ν|y1,···,yn),即價格序列關(guān)于總交易量序列生成的信息流為鞅. 另外,對擁有不完全信息的內(nèi)部交易者,令 其中, 文獻[3]或文獻[4]中已經(jīng)說明當(dāng)內(nèi)部交易者多于一個時,純策略均衡不存在,因此要在混合策略空間中求解其混合策略均衡.記原概率空間為(?,F,P),用來刻畫市場的隨機性,則風(fēng)險資產(chǎn)的清算價值ν(ω),噪聲交易者第n期交易量μn(ω)和不完全信息的內(nèi)部交易者知道風(fēng)險資產(chǎn)的部分信息(ν+ε)(ω)都是該空間上的隨機變量,用(···)表示該空間中的數(shù)學(xué)期望,條件期望與方差等類似.假設(shè)存在另一個離散概率空間,用來刻畫內(nèi)部交易者交易的隨機性,特別地,其交易策略系數(shù) βin是其上的一個隨機變量,記為.假設(shè)在每一期,內(nèi)部交易者選擇參加交易或者不參加交易的概率相等,都為1/2,并且每一期各個內(nèi)部交易者的交易策略系數(shù)是相互獨立的.用(···)表示此空間中的數(shù)學(xué)期望,其余類似.因此,內(nèi)部交易者i在第n期的交易量,第n期的收益,剩余信息量 第n期總交易量 在本文模型中,有如下均衡定義: (1)利潤最大化條件:根據(jù)內(nèi)部交易者對待風(fēng)險的態(tài)度選擇如下策略最大化其相關(guān)利潤, (2)市場有效性條件:做市商按如下方式確定第n期的價格, 其中,內(nèi)部交易者i在第n期的交易策略系數(shù)βin的概率分布為: 而i=1,2,an,bn為實數(shù),且an0,bn0,n=1,2,···,N,而這些交易策略系數(shù)是獨立的. 在混合策略空間上,對兩個擁有不完全信息的內(nèi)部交易者有如下引理: 引理 2.1設(shè) 對所有的n>0有以下等式成立: 注 2.1該引理的證明與文獻[6]或文獻[7]中相關(guān)引理的證明方法類似. 利用與文獻[6]或文獻[7]中類似的方法可以證明下述命題. 命題 2.1在市場有效性條件下,若擁有不完全信息的兩個內(nèi)部交易者采取的策略形式為(2.1)式,那么,內(nèi)部交易者i的平均預(yù)期未來總收益為: 與文獻[2]類似,根據(jù)內(nèi)部交易者對待風(fēng)險的態(tài)度不同考慮如下三個模型.在第n期,在給定其他內(nèi)部交易者最優(yōu)策略的條件下: 模型 1(風(fēng)險喜好型內(nèi)部交易者模型) 內(nèi)部交易者i首先最大化風(fēng)險收益,即maxβinci,n?1,若解不唯一,則在這些解中最大化保底收益,即maxβin∈argmax ci,n?1di,n?1; 模型 2(風(fēng)險中性型內(nèi)部交易者模型) 內(nèi)部交易者i最大化事前預(yù)期收益,即 模型 3(風(fēng)險厭惡型內(nèi)部交易者模型) 內(nèi)部交易者i首先最大化保底收益,即maxβindi,n?1,若解不唯一,則在這些解中最大化風(fēng)險收益,即maxβin∈argmax di,n?1ci,n?1. 在考慮多期交易模型前,先給出單期的情形,即N=1的情況.與文獻[4]類似,在單期情形,模型1,模型2,模型3的均衡是一樣的且有如下定理: 定理 2.1兩個擁有不完全信息的內(nèi)部交易者的單期模型存在唯一的一個混合策略均衡,且在均衡狀態(tài)下: 其中i=1,2,a=b>0且a2是方程16x3?9x2?9x?2=0的唯一正根. 定理 3.1在有兩個擁有不完全信息的風(fēng)險喜好內(nèi)部交易者的N期模型1中存在唯一的一個混合策略均衡,且在均衡狀態(tài)下有, 數(shù)列{an},{cn},{dn}由下列等式唯一遞推確定: 其中n=1,2,···,N,cN=dN=0. 證明 利用逆向歸納法,由命題2.1和定理2.1可知,當(dāng)n=N時,(3.1)式,(3.2)式,(3.3)式成立. 一般地,假設(shè)在第n+1期(n≤N?1),有 且在第n+1期(3.1)式,(3.2)式,(3.3)式成立,那么在第n期有, 從 di,n?1的表達式可以看出,d1,n?1與 d2,n?1相等,即d1,n?1=d2,n?1=dn?1. 在第n期,對于擁有不完全信息的內(nèi)部交易者1有, 根據(jù)一階條件有, 同理,在第n期,對于擁有不完全信息的內(nèi)部交易者2有, 根據(jù)一階條件有, 記最優(yōu)策略中的an,bn為,則由博弈論的相關(guān)知識可知,為 Nash均衡,且滿足以下條件: (i)對任意的an,有 (ii)對任意的bn,有 顯然,對任意的an,bn,有 由以上三個式子可得, (iii)對任意的an,有 (iv)對任意的bn,有 若 c1,n?1(a?n,b?n)c1,n?1(b?n,a?n),不妨設(shè) 綜上可得, 因為對每個內(nèi)部交易者來說,在第n期都會選擇最優(yōu)策略以獲取最大收益,故 即 可得an=bn或anbn=2. 假設(shè)anbn=2且anbn成立,下面證矛盾. 由anbn=2,an0,知bn=,聯(lián)立兩個一階條件式并消去cn,整理化簡可得, 可以看出,得到的方程與完全信息下存在兩個風(fēng)險喜好的內(nèi)部交易者時得到的方程一樣,所以利用與文獻[4]模型1中類似的方法可以證得an=bn.因此, 其中n≤N?1,即(3.1)式,(3.2)式,(3.3)式成立. 綜上可知,對任意的n=1,2,···,N,(3.1)式,(3.2)式和(3.3)式都成立. 下面證明an的存在性.令 則fn(0)=>0, 由(3.1)式得, 因此fn(0)>0而fn(aN)<0,由fn(x)的連續(xù)性知,存在an=∈(0,aN)使(3.3)式成立.特別地,由于 可見函數(shù)fN(x)關(guān)于y軸對稱,且在區(qū)間(0,aN)上fN(x)>0,在(aN,∞)上fN(x)<0.所以,可以假設(shè)在第n+1期(n≤N?1)有cn>cn+1≥0,且在區(qū)間(0,an+1)上fn+1(x)>0,在(an+1,∞)上fn+1(x)<0.由于cn>cn+1,明顯 由此知, 且在區(qū)間(an+1,∞)上fn(x) 下面證明an的唯一性.由(3.1)式知,cn唯一地由cn+1與an+1確定,它僅在最優(yōu)策略中的an處滿足(3.3)式,不能被認為是an的函數(shù).所以 由(3.3)式可知, 定理 3.2在有兩個擁有不完全信息的風(fēng)險中性內(nèi)部交易者的N期模型2中存在唯一的一個混合策略均衡,且在均衡狀態(tài)下有, 數(shù)列{an},{cn},{dn}由下列等式唯一遞推確定: 其中n=1,2,···,N,cN=dN=0. 注 3.1類似于定理3.1的證明方法可以證明上述定理3.2,在此省略. 定理 3.3在有兩個擁有不完全信息的風(fēng)險厭惡內(nèi)部交易者的N期模型3中存在唯一的一個混合策略均衡,且在均衡狀態(tài)下有, 數(shù)列{an},{cn},{dn}由下列等式唯一遞推確定: 其中n=1,2,···,N,cN=dN=0. 注 3.2類似于文獻[4]模型3中定理的證明方法可以證明該定理,在此省略. 本節(jié)研究當(dāng)交易時間間隔?tN趨于零時,上述離散均衡中各參數(shù)的極限行為與漸近行為.對于t∈[0,1),設(shè)[Nt]為Nt的整數(shù)部分,求解a[Nt]等參數(shù)趨于極限的速度,并對這些參數(shù)進行漸近分析. 注意到,由定理3.1中(3.1)式與(3.3)式得到的關(guān)于序列an的方程與完全信息下存在兩個風(fēng)險喜好的內(nèi)部交易者時得到的方程一樣.因此得到了與文獻[5]模型1中同樣的命題,以該命題為基礎(chǔ),有如下定理: 定理 4.1當(dāng) N → ∞,即 ?tN→ 0時,模型 1的 N 期離散均衡結(jié)果都是收斂的,對 t∈[0,1), 進一步,有如下結(jié)果: (1)交易策略參數(shù)滿足: 滿足隨時間t單調(diào)遞增; (2)與歷史信息正交的私有信息量滿足: 滿足隨時間t單調(diào)遞減趨于零; (3)擁有不完全信息的內(nèi)部交易者未釋放的信息量滿足: 滿足隨時間t單調(diào)遞減,且交易結(jié)束時, (4)市場流動性參數(shù)滿足: 滿足隨時間t單調(diào)遞增. 證明此定理的證明分為三部分.第一部分證明當(dāng)N→∞時,a[Nt]的極限為0以及c[Nt], d[Nt]均趨于無窮大;第二部分求解 a[Nt],c[Nt],d[Nt]趨于各自極限的速度;第三部分利用前兩部分的結(jié)果,討論交易策略參數(shù),與歷史信息正交的私有信息量參數(shù),內(nèi)部交易者未釋放的信息量參數(shù)和市場流動性參數(shù)的漸近性質(zhì). 第一部分利用與文獻[5]模型1中類似的方法可以證得(4.1)式,(4.2)式,(4.3)式成立. 第二部分求解a[Nt],c[Nt],d[Nt]趨于各自極限的速度,關(guān)鍵在于求解a[Nt]→0的速度.由于得到了與文獻[5]模型1中關(guān)于序列an一樣的遞推關(guān)系式,所以,不完全信息下a[Nt]→0的速度與完全信息下a[Nt]→0的速度是一樣的,故 可見(4.4)式成立. 依據(jù)(3.1)式關(guān)于an項的2階泰勒展開,并舍去高階無窮小項,可得 設(shè) 其中n=[Nt],[Nt]為Nt的整數(shù)部分,?t=?tN,表示ct關(guān)于t的導(dǎo)數(shù),以下類似. 于是,(4.10)式可以化為: 令等式兩邊同時除以?t1/2,可得微分方程 于是,由c1=0可得 綜上可得, 可見(4.5)式成立. 同理,由(3.2)式可得 設(shè) 其中n=[Nt],[Nt]為Nt的整數(shù)部分,?t=?tN. 于是,(4.11)式可以化為: 可見, 由d1=0,可解得 綜上可得, 可見(4.6)式成立. 第三部分利用前兩部分的結(jié)果,討論其他參數(shù)的漸近性質(zhì). (1)交易策略參數(shù)的漸近行為分析: 由本文模型中βn的分布以及an=bn,可得 滿足隨時間t單調(diào)遞增. (2)與歷史信息正交的私有信息量參數(shù)的漸近行為分析: 由引理2.1知, 且βin與Hn?1相互獨立.因此, 將(4.12)式對an項進行2階泰勒展開,并舍去高階無窮小項,可得 從而E(H[Nt])的極限E(Ht)滿足: 初始條件滿足: 求解上述微分方程,可以得到解的表達式 滿足隨時間t單調(diào)遞減趨于零. (3)擁有不完全信息的內(nèi)部交易者未釋放的信息量參數(shù)的漸近行為分析: 由引理2.1可知, 將(4.12)式代入上式得 將上式對an項2階泰勒展開,并舍去高階無窮小項得 從而E(Σ[Nt])的極限E(Σt)滿足: 初始條件滿足: 求解上述微分方程,可得 滿足隨時間t單調(diào)遞減,且交易結(jié)束時, (4)市場流動性參數(shù)的漸近行為分析: 由引理2.1知, 且βin與Hn?1相互獨立,所以 將(4.12)式代入上式,可得 對an項進行2階泰勒展開,并舍去高階無窮小項,可得 滿足隨時間t單調(diào)遞增. 由定理4.1可獲得如下模型1的經(jīng)濟金融意義: (1)當(dāng)市場中存在兩個風(fēng)險喜好的內(nèi)部交易者時,風(fēng)險喜好內(nèi)部交易者的交易強度隨著時間t由低到高變化,在交易結(jié)束時達到最大值;這與文獻[6]或文獻[7]中模型1當(dāng)市場中存在一個擁有不完全信息的風(fēng)險喜好內(nèi)部交易者時結(jié)果一致,且與文獻[5]模型1中的完全信息下存在兩個風(fēng)險喜好內(nèi)部交易者時的交易策略參數(shù)相等.這說明當(dāng)市場中存在兩個風(fēng)險喜好的內(nèi)部交易者時,完全信息下內(nèi)部交易者的交易強度與不完全信息下內(nèi)部交易者的交易強度一致. (2)一方面,當(dāng)信息的不完全程度σε固定時,關(guān)于資產(chǎn)ν的真實價值信息不斷釋放,且在交易的前半段具有較小的釋放速度,后半段具有更大的釋放速度.這說明風(fēng)險喜好的內(nèi)部交易者喜歡保留信息優(yōu)勢以獲得更多的未來收益.另一方面,未釋放到公開市場的信息量是關(guān)于信息不完全程度σε的增函數(shù),即σε越大(此時內(nèi)部交易者的信息越不完全),資產(chǎn)ν的真實價值未釋放的信息量越多.這與文獻[6]或文獻[7]中模型1的結(jié)果一致.另外,與文獻[5]模型1的情形相比較知,當(dāng)兩個內(nèi)部交易者信息完全時剩余信息量滿足: 由(4.8)式可以得到, 由此可見,在交易過程中不完全信息的內(nèi)部交易者的私有信息剩余量比完全信息的內(nèi)部交易者的私有信息剩余量多,并且σε越大,私有信息的剩余量相差就越大. (3)一方面,當(dāng)σε固定時,市場流動性參數(shù)滿足隨著時間t單調(diào)遞增,剛開始時保持較低,后來較大.這是因為前期私有信息的使用速度較慢,后期私有信息的使用速度較快.這說明風(fēng)險喜好的內(nèi)部交易者喜歡把私有信息的釋放集中于后期,即后期的交易蘊含更多的私有信息.另一方面,市場流動性參數(shù)是關(guān)于σε的減函數(shù),即σε越大,市場流動性參數(shù)越小.這與文獻[6]或文獻[7]中模型1的結(jié)果一致.另外,與文獻[5]模型1的情形相比較可知,當(dāng)兩個內(nèi)部交易者信息完全時市場流動性參數(shù)滿足: 由(4.9)式可以得到, 由此可見,信息完全的內(nèi)部交易者的市場流動性參數(shù)始終大于信息不完全的內(nèi)部交易者的市場流動性參數(shù),并且σε越大,市場流動性參數(shù)相差就越大. 由定理3.2中(3.4)式,(3.5)式,(3.6)式可以得到與文獻[5]模型2中同樣的命題,以該命題為基礎(chǔ),類似于定理4.1的證明方法,有如下定理: 定理 4.2當(dāng) N → ∞,即 ?tN→ 0時,模型 2的 N 期離散均衡結(jié)果都是收斂的,對 t∈[0,1), 進一步,有如下結(jié)果: (1)交易策略參數(shù)滿足: 滿足隨時間t單調(diào)遞增; (2)與歷史信息正交的私有信息量滿足: 滿足隨時間t單調(diào)遞減,且交易結(jié)束時E(H1)=H0e?2>0; (3)擁有不完全信息的內(nèi)部交易者未釋放的信息量滿足: 滿足隨時間t單調(diào)遞減,且交易結(jié)束時, (4)市場流動性參數(shù)滿足: 根據(jù)定理4.2可類似獲得模型2的經(jīng)濟金融意義,在此省略. 同樣,由定理3.3中式(3.7),式(3.8),式(3.9)可以得到與文獻[5]模型3中同樣的命題,以該命題為基礎(chǔ),類似于定理4.1的證明方法,有如下定理: 定理 4.3當(dāng) N → ∞,即 ?tN→ 0時,模型 3的 N 期離散均衡結(jié)果都是收斂的,對 t∈[0,1), 進一步,有如下結(jié)果: (1)交易策略參數(shù)滿足: 滿足隨時間t單調(diào)遞增; (2)與歷史信息正交的私有信息量滿足: 滿足隨時間t單調(diào)遞減趨于零; (3)擁有不完全信息的內(nèi)部交易者未釋放的信息量滿足: 滿足隨時間t單調(diào)遞減,且交易結(jié)束時, (4)市場流動性參數(shù)滿足: 滿足隨時間t單調(diào)遞增. 根據(jù)定理4.3也可類似獲得模型3的經(jīng)濟金融意義,在此省略. [1]Kyle A S.Continuous auctions and insider trading[J].Econometrica,1985,53(6):1315-1335. [2]Gong F,Zhou D.Insider Trading in the market with Rational Expected Price[EB/OL].arXiv:2010,1012. 2160v1[q-f i n.TR]. [3]Gong F,Liu H.The Mixed Equilibrium of Insider Trading in the Market with Rational Expected Price[C]// Tusheng Zhang,Xinyu Zhou.Stochastic analysis and Applications to Finance.Singapore:World Scientif i c, 2012. [4]張首元.兩個內(nèi)部交易者的內(nèi)部交易問題研究[D].北京:北京科技大學(xué),2012. [5]劉舉款.高頻交易情況下兩個內(nèi)部交易者的混合策略均衡的漸近分析[D].長沙:長沙理工大學(xué),2013. [6]紀(jì)曉燕,鞏馥洲.不完全信息下風(fēng)險喜好的內(nèi)部交易者模型的均衡解及漸近分析 [J].應(yīng)用數(shù)學(xué)學(xué)報, 2014,37(2):1-9. [7]紀(jì)曉燕.不完全信息下的內(nèi)部交易[D].長沙:長沙理工大學(xué),2012. The analysis of trading behavior with two insiders when the information is incomplete Gong Fuzhou1,Shang Hongyuan2 According to the dif f erence of insiders′risk attitude,three dif f erent models-risk-seeking insiders′model,risk-neutral insiders′model and risk-averse insiders′model are given in the f i nancial market where there exists two insiders who own the same incomplete information.The discrete time equilibrium and asymptotic behavior of high frequency trading in the mixed strategy space are proved for the three models respectively. Furthermore,the economic characteristics for the three models are also analysed. incomplete information,insider trading,mixed strategy equilibrium,high frequency trading, asymptotic analysis O211.6;O211.9 A 1008-5513(2014)02-0111-18 10.3969/j.issn.1008-5513.2014.02.001 2014-04-03. 國家自然科學(xué)基金(17021101). 鞏馥洲(1965-),博士,研究員,研究方向:隨機分析. 2010 MSC:60G05


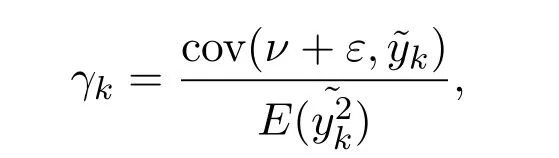

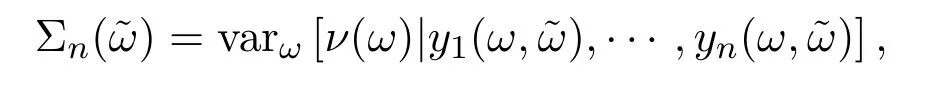
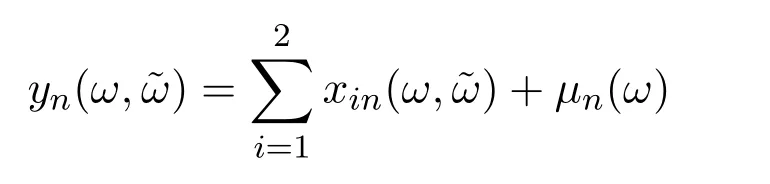
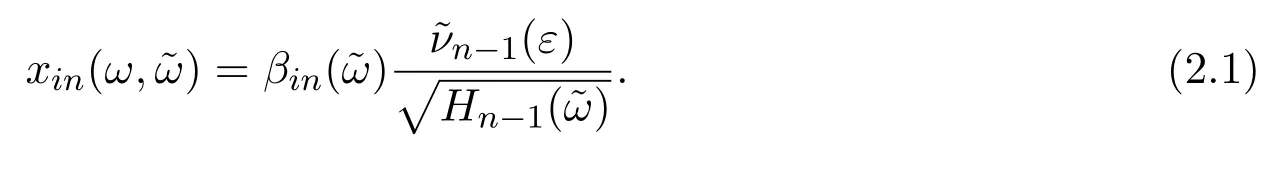



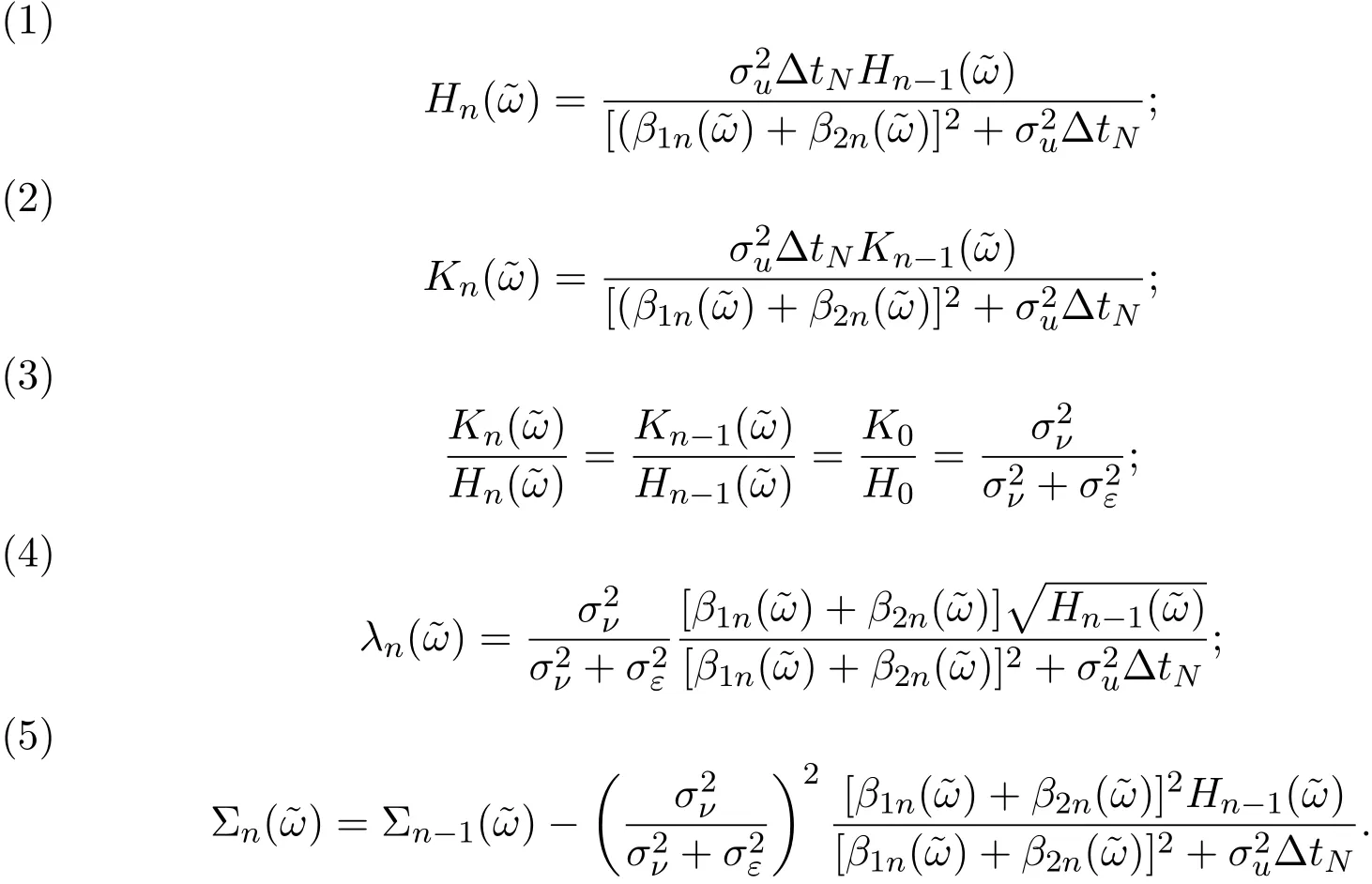

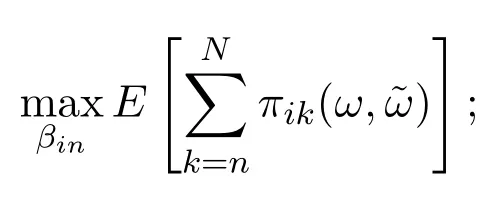
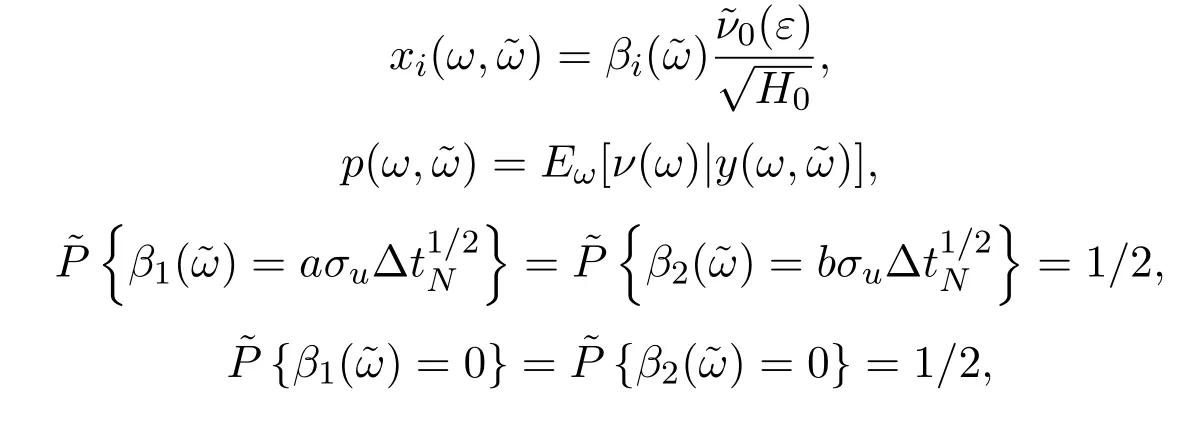
3 三個模型混合策略均衡存在唯一性的證明

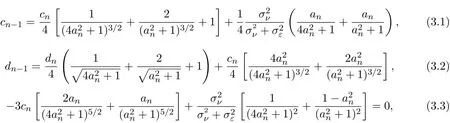


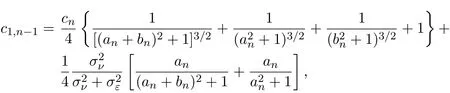












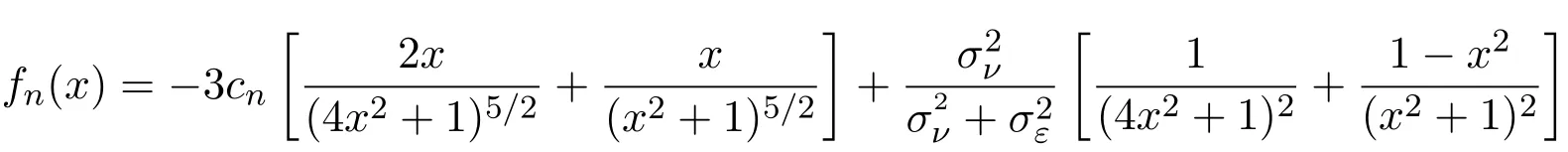

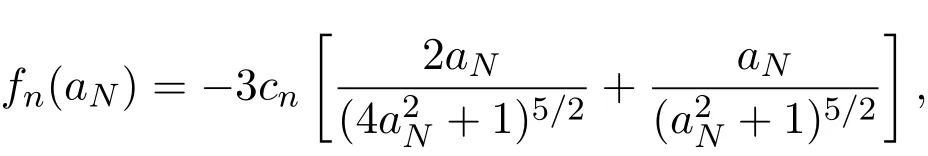





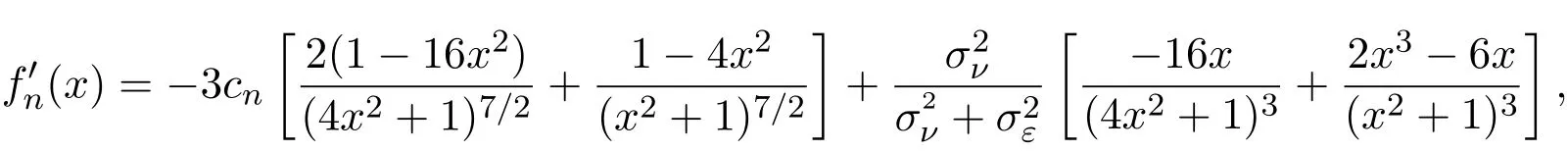

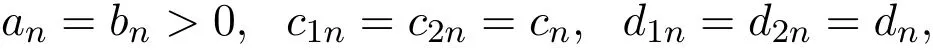

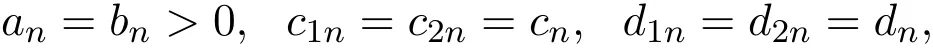

4 三個模型混合策略均衡高頻交易的漸近分析


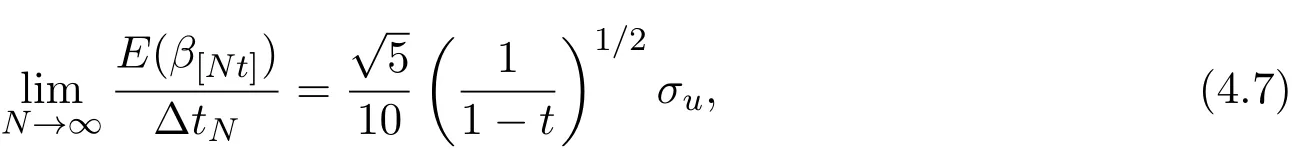

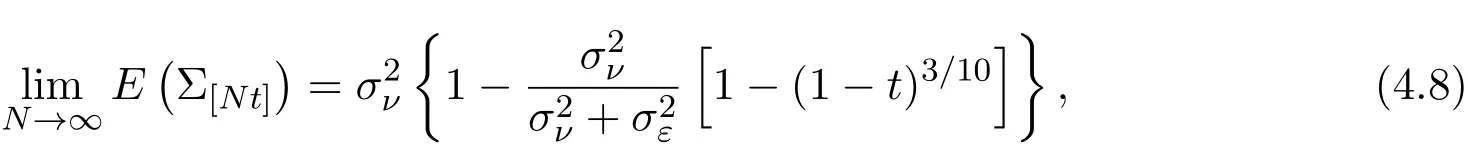


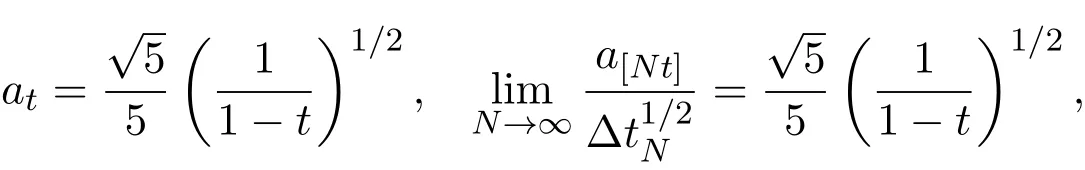




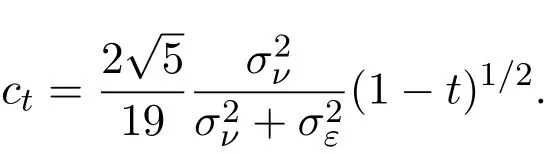
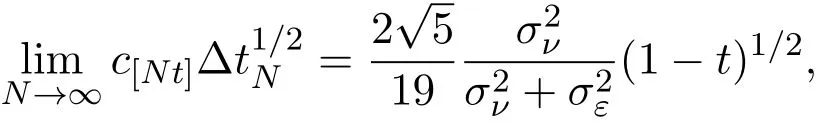

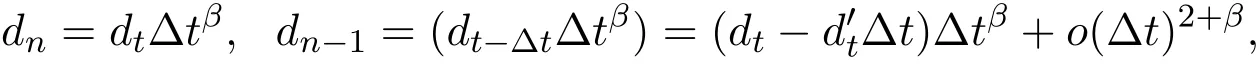








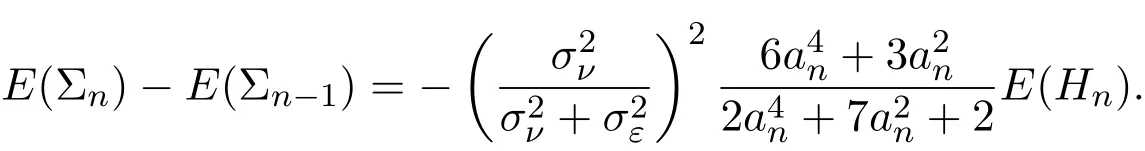
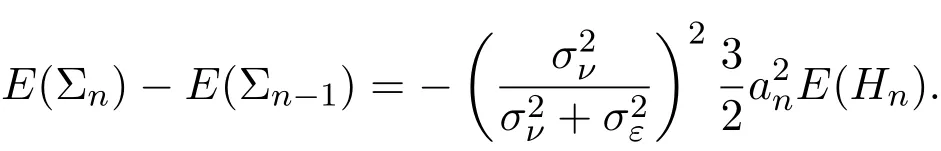

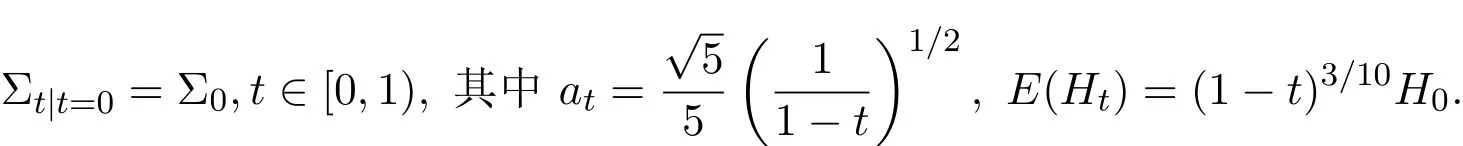



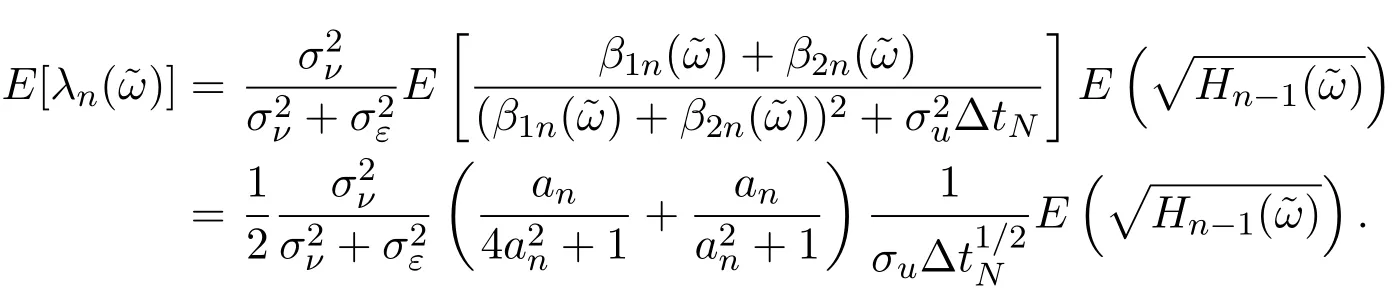
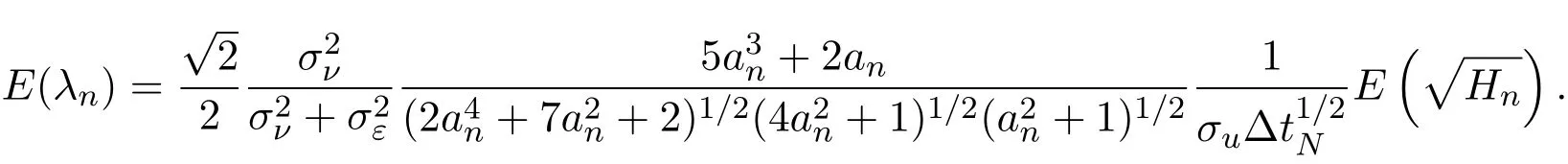


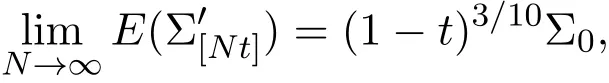
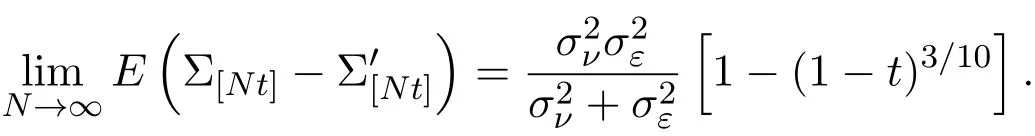

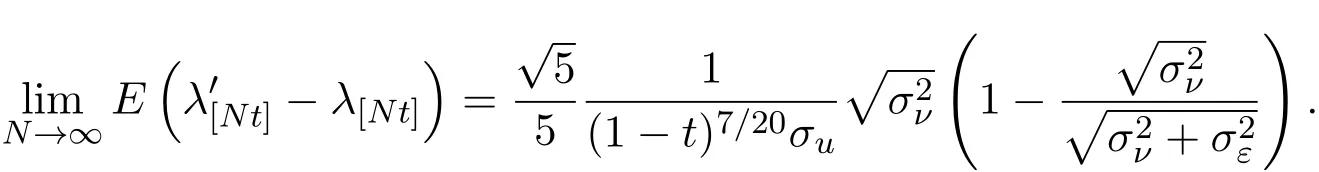

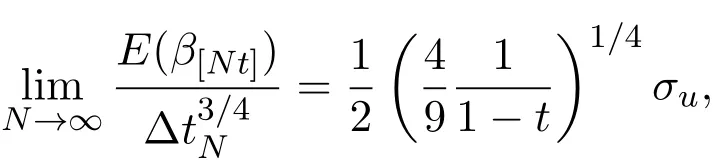
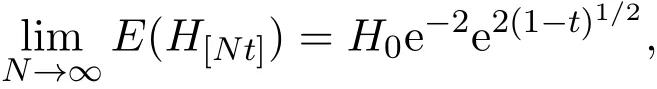
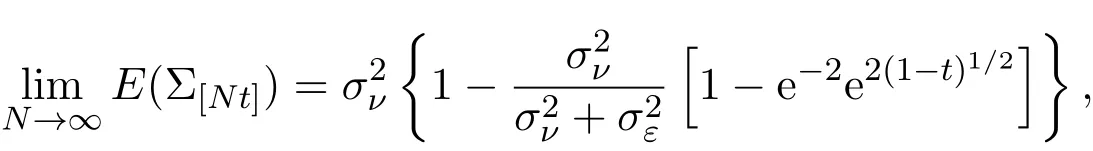
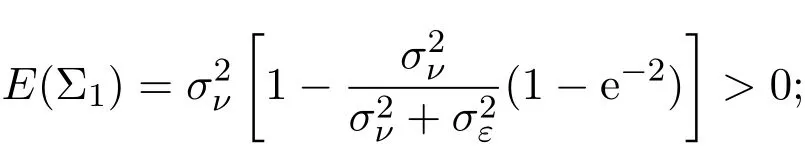
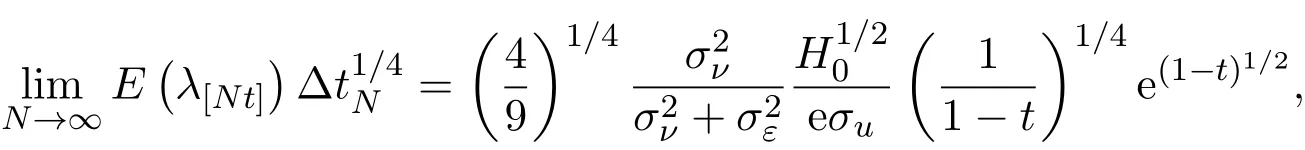
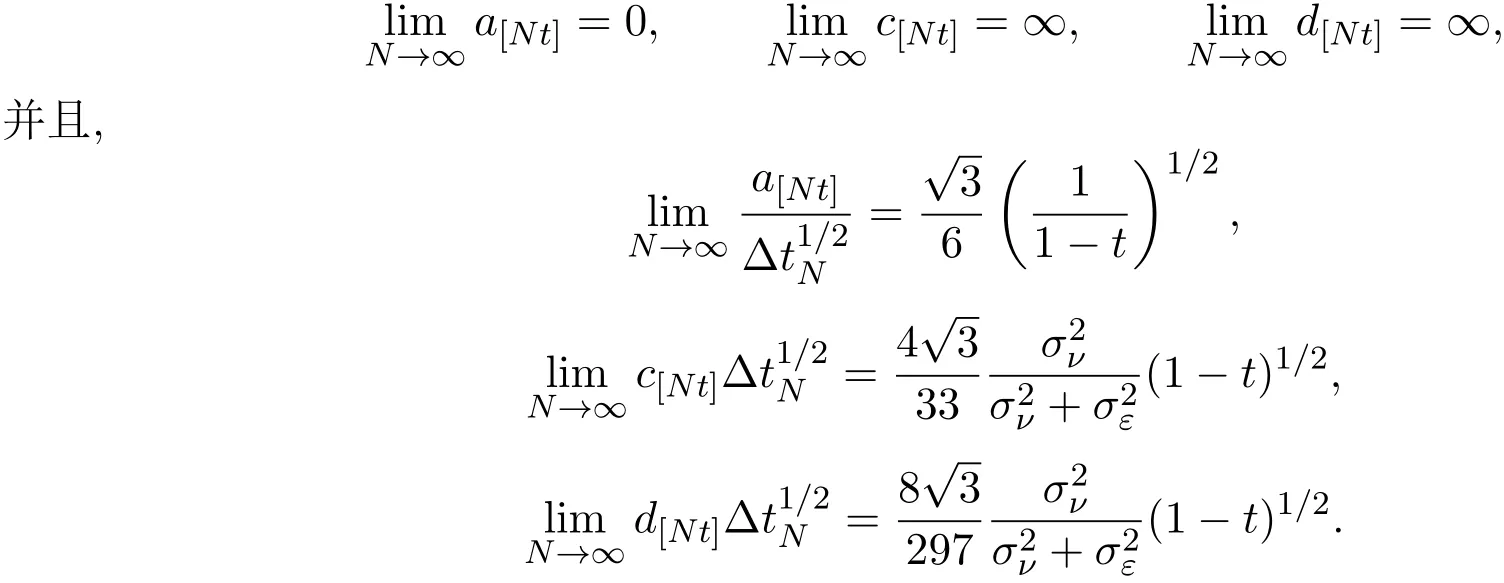
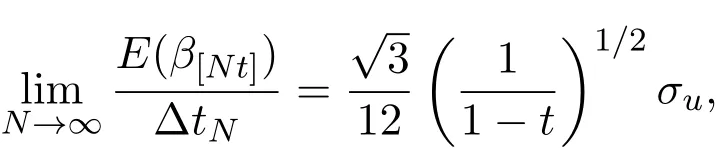
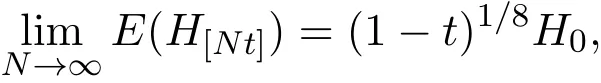
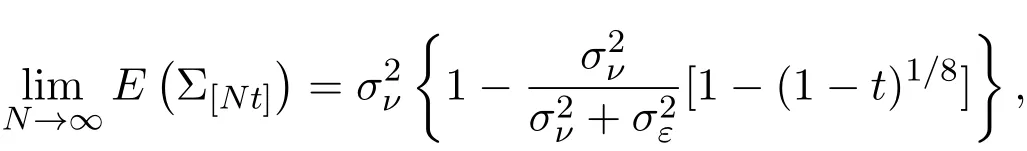
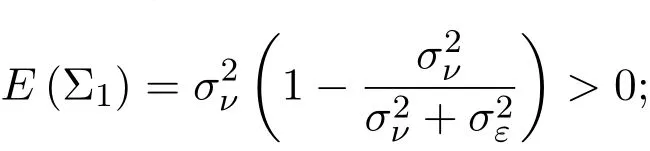

(1.Academy of Mathematics and System Science,Chinese Academy of Sciences,Beijing 100190,China; 2.School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China)

