一種自適應預處理的BiCRSTAB算法
張晉, 李春光, 景何仿
(1.北方民族大學數(shù)學與科學學院,寧夏 銀川 750021; 2.北方民族大學數(shù)值計算與工程應用研究所,寧夏 銀川 750021)
一種自適應預處理的BiCRSTAB算法
張晉1, 李春光2, 景何仿2
(1.北方民族大學數(shù)學與科學學院,寧夏 銀川 750021; 2.北方民族大學數(shù)值計算與工程應用研究所,寧夏 銀川 750021)
提出一種自適應預處理的BiCRSTAB方法,該預處理可以看作一個隱式構造多項式的預處理方法,由BiCRSTAB算法中嵌入幾步GMRES迭代自適應構造而成.數(shù)值算例表明,該方法能有效減少迭代步數(shù),從而減少計算過程中的貯存量和運算量.
線性方程組;自適應預處理;BiCRSTAB算法;GMRES算法
1 引言
但是,對于實際應用中某些復雜的問題,BiCRSTAB方法仍然存在收斂速度緩慢或是收斂行為不規(guī)則的現(xiàn)象,為了克服這些問題,本文后面將提出一種自適應預處理的BiCRSTAB方法,該方法可以看作一種隱式的構造多項式預處理方法,它由BiCRSTAB算法中嵌入幾步GMRES[1]迭代自適應構造而成.能有效地減少迭代步數(shù),降低存儲量和運算量,運算時間也相應的減少.
2 一種自適應預處理的BiCRSTAB算法
數(shù)值實驗表明BiCRSTAB算法收斂速度比BiCR算法快而且更加穩(wěn)定,然而在一些實際問題應用中,BiCRSTAB算法收斂得很慢甚至會停滯.因此如何選擇適當?shù)念A條件子成為BiCRSTAB算法高效求解這類問題的關鍵.下面給出原始預條件的BiCRSTAB算法:
算法 1原始預條件的BiCRSTAB算法
1.對于給定的x0,計算r0=b?Ax0;
2.令p0=r0,q0=AM?1r0,=q0,=;
3.For j=1,2,···,直到收斂
10.rj+1=sj?ωjtj;
14.pj+1=rj+1+βj(pj?ωjqj);
17.End.
算法1的每一步迭代都需要計算M?1rj和M?1qj,也就是說,每一步迭代都需要計算M?1v這樣的形式,預條件的關鍵就是使AM?1近似于一個單位矩陣,即

可以得到M?1v近似于A?1v,而在某種程度上來講M 應與A近似.
下面給出一個新的BiCRSTAB算法預處理矩陣M的隱式構造過程,亦即對任一給定的n維向量z,當需要計算M?1v=z時,都轉化為用k步GMRES求解方程組Mv=z,其中k常取2或3,m的值由具體問題來確定的.根據(jù)上述過程,可用迭代結果M?1z作為近似值,其中初始向量v0取為零向量,算法中的隱式構造預處理實際是一個多項式預處理,證明見文獻 [3].
算法 2一種自適應預處理的BiCRSTAB算法
1.對于給定的x0,計算r0=b?Ax0,選擇=P(A)r0;
3.For j=1,2,···,直到收斂
5.αj=
6.sj=rj?αjqj;
8.tj=
9.ωj=
10.xj+1=
11.rj+1=sj?ωjtj;
15.βj=
16.pj+1=rj+1+βj(pj?ωjqj);
18.qj+1=
19.End.
3 數(shù)值算例
下面給出幾個數(shù)值算例來比較原始的BiCRSTAB算法,BiCR算法,以及自適應預條件的BiCRSTAB算法的執(zhí)行結果.為了使數(shù)值結果便于重復,這里具體給出各參數(shù)的值,而不考慮算法的執(zhí)行細節(jié).選取右端向量b使得方程組Ax=b的精確解為xT=(1,1,···,1),預初始估計值為=(0,0,···,0).
例 1本算例中的系數(shù)矩陣A取自文獻[4],具有如下形式:
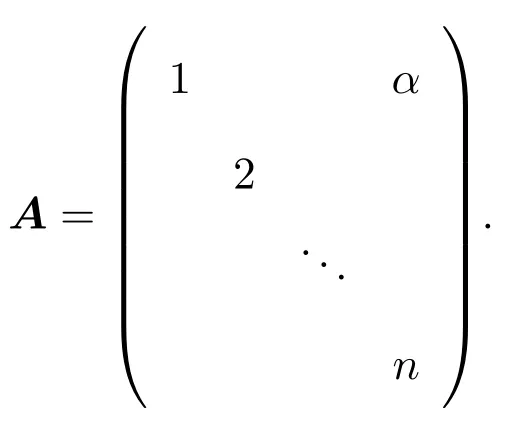
取求解精度Tol=10?8,矩陣階數(shù)n=2000,當α=20000時,A是典型的非對稱矩陣,當α=1.1時,系數(shù)矩陣A接近對稱矩陣,三種方法得到迭代收斂效果如圖1,圖2所示.
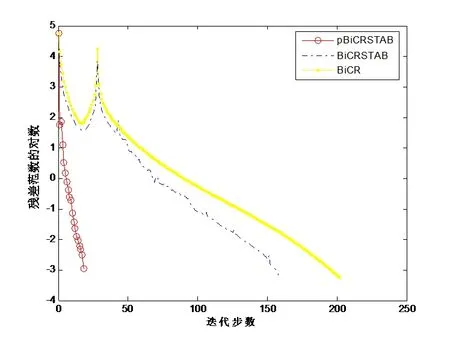
圖1 算例1的數(shù)值結果(α=20000)

圖2 算例1的數(shù)值結果(α=1.1)
例 2本算例中的系數(shù)矩陣A=CDC?1,C為n階的隨機矩陣,
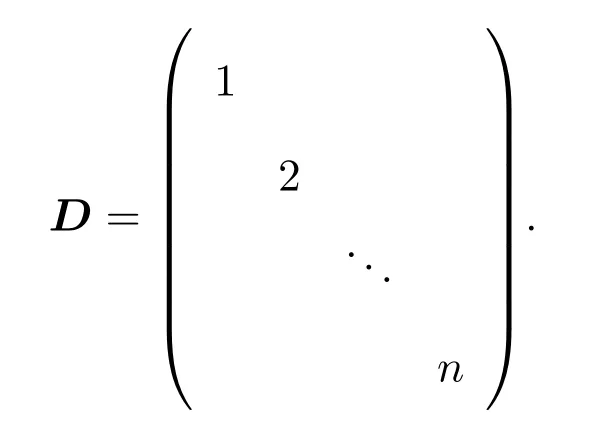
當Tol=10?8,n=2000時,得到迭代收斂效果如圖3所示.
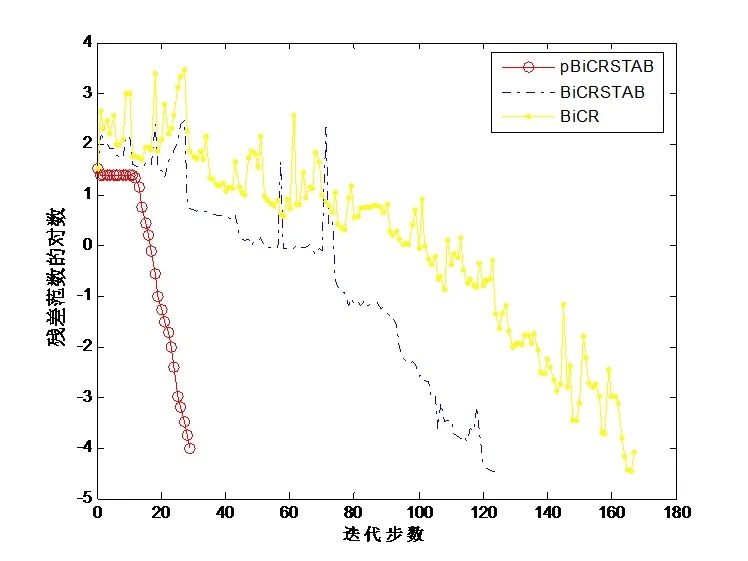
圖3 算例2的數(shù)值結果
例 3本算例的系數(shù)矩陣A取自文獻[5],A=SBS?1,

當Tol=10?8,n=2000時,得到迭代收斂效果如圖4所示.
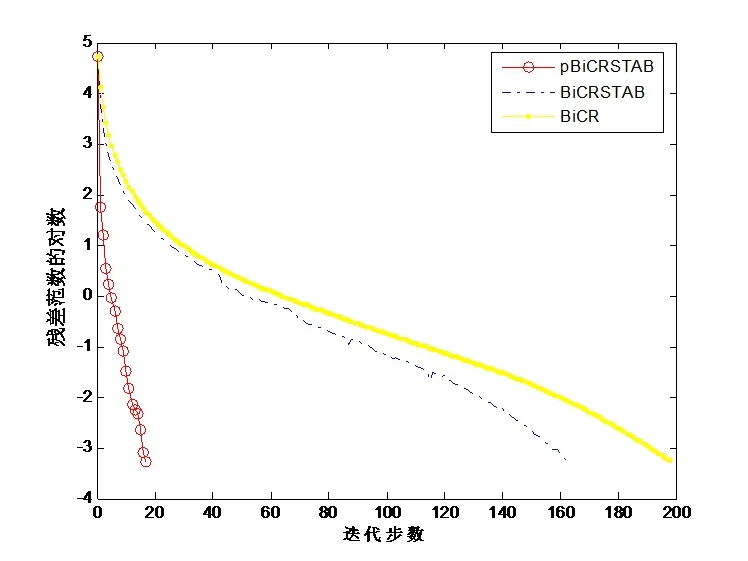
圖4 算例3的數(shù)值結果
例 4[6]考慮如下二階橢圓形偏微分方程
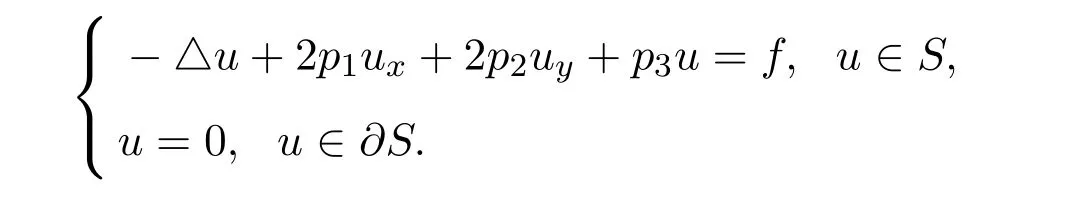
其中,S={(x,y)∈R2,0 我們用中心差分離散方程,把區(qū)域S劃分成網(wǎng)格尺寸為h=1/l+1的(l+2)×(l+2)個均勻正方形網(wǎng)格,網(wǎng)格點為si=ih,tj=jh,0≤i,j≤l+1.整個方程被離散成五點格式,把網(wǎng)格點按自然次序排序得l2×l2塊三對角矩陣: 其中,γ=p1h,β=p2h,σ=p3h,線性系統(tǒng)右端的元素為h2f(si,tj),為簡單起見以下算例右端向量取b=sum(A,2),以下取l=50,p1=25,p2=50,p3=30得到的結果如圖5所示. 圖5 算例4的數(shù)值結果 下面給出pBiCRSTAB算法,BiCRSTAB算法以及BiCR算法三類算法的迭代次數(shù)及計算時間比較,見表1,表2. 本文提出一種求解大型系數(shù)線性方程組的自適應BiCRSTAB算法,在每一步外迭代中的預處理子是不斷變化的.數(shù)值算例表明,新算法與原始的BiCRSTAB算法相比較,迭代次數(shù)減少同時收斂速度加快. 表1 各方法的迭代次數(shù)比較 表2 各方法的CPU時間比較 [1]Saad Y.Iterative Methods for Sparse Linear Systems[M].Boston:PW Publishing Company,1996. [2]Abe K,Sleijpen G L G.BiCR variants of the hybrid BiCG methods for solving linear systems with nonsymmetric matrices[J].Comput.Appl.Math.,2010,234:985-994. [3]Cao H Y,Li X W.CGS/GMRES(k):An adaptive preconditioned CGS algorithm for nonsymmetric linear systems[J].Numer.Math.,1998,7:145-158. [4]Niu Q,Lu L Z,Wang R R.A modif i ed GMRES method for solving large nonsymmetric linear systems[J].高等學校計算數(shù)學學報,2005,27:193-199. [5]Sadok H.CMRH:A new method for solving nonsymmetric linear systems based on the Hessenberg reduction algorithm[J].Numerical Algorithm,1999,20:303-321. [6]全中,向淑晃.基于GMRES的多項式預處理廣義極小殘差法[J].計算數(shù)學,2006,28(4):365-376. An adaptive preconditioned BiCRSTAB algorithm for linear Zhang Jin1,Li ChunGuang2,Jin HeFang2 An adaptive preconditioned BiCRSTAB is presnted,which which is combined with an polynomial preconditioner constructed implicitly,and several steps of GMRES are inserted in BiCRSTAB algorithm.Numerical experiments illustrate this method can reduce the iterative steps and computation time ef f ectively. linear systems,adaptive preconditioning,BiCRSTAB,GMRES O241.6 A 1008-5513(2014)02-0195-06 10.3969/j.issn.1008-5513.2014.02.011 2013-12-26. 國家自然科學基金重大研究計劃培育項目(91230111);寧夏自然科學基金(NZ13086);國家自然科學基金(11361002). 張晉(1987-),碩士生,研究方向:數(shù)值代數(shù). 李春光(1964-),教授,博士生導師,研究方向:流體力學與計算數(shù)學. 2010 MSC:65F10
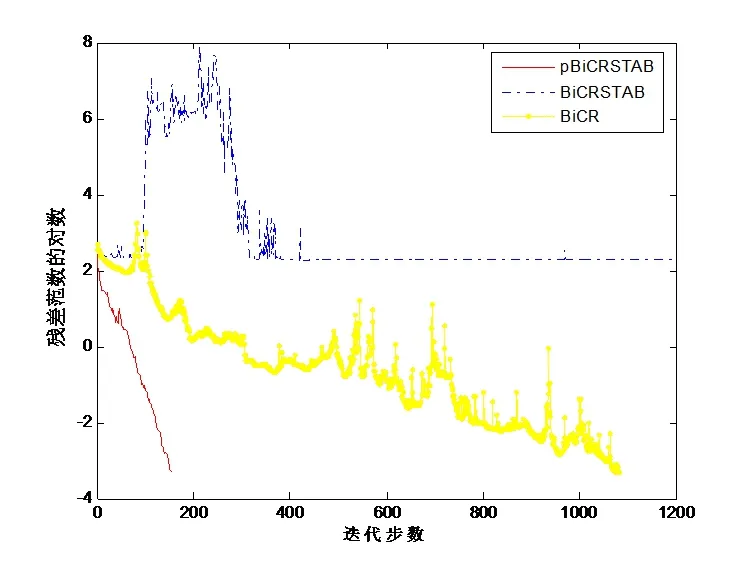
4 結論


systems
(1.School of Mathematics and Information Science,Beifang University of Nationnalities, Yinchuan 750021,China; 2.Institute of Numerical Computation and Engineering Application,Beifang University of Nationnalities, Yinchuan 750021,China)

