帶約束集值均衡問題的近似Henig有效解
胡莎莎,徐義紅,牛智超
(南昌大學(xué)數(shù)學(xué)系,江西 南昌330031)
1.引言
向量均衡問題是許多實際領(lǐng)域中的一個廣泛問題.它涵蓋了許多典型的數(shù)學(xué)問題,如向量優(yōu)化,變分不等式,向量納什均衡,向量互補等.它廣泛應(yīng)用于投資決策,定量經(jīng)濟(jì),最優(yōu)控制和工程技術(shù).由于所涉問題的普遍性和統(tǒng)一性以及解決這些問題之普遍,向量均衡問題已成為運籌學(xué)和非線性分析領(lǐng)域的熱點問題[1?6].LONG等[1]在近似錐次類凸性假設(shè)下獲得了帶函數(shù)約束的向量均衡問題Henig有效解的最優(yōu)性條件.Luu等[2?3]建立了帶等式和不等式約束的向量均衡問題有效解的充分和必要條件,同時建立了帶約束向量均衡問題局部有效解的Fritz-John和Karush-Kuhn-Tucker最優(yōu)性必要條件.GONG[4?6]在錐凸性假設(shè)下獲得了帶約束向量均衡問題有效解的最優(yōu)性條件,在Banach空間中利用非線性泛函和Ioffe次可微獲得了非凸向量均衡問題弱有效解,Henig有效解,超有效解以及全局有效解的最優(yōu)性條件.
Gerth等[7]利用非凸分離定理,得到了弱有效點和真有效點的標(biāo)量化結(jié)果.借助Gerstewitz函數(shù),LI等[8]建立了集值非凸優(yōu)化問題的必要和充分最優(yōu)性條件.在沒有任何凸性假設(shè)下,ZHENG[9]利用連續(xù)單調(diào)Minkowski泛函,獲得了賦范空間中Henig有效點的標(biāo)量化特征.
另外,在非緊可行集的情況下,精確解集有可能是空集,而在條件較弱情況下,近似解集可以是非空的.因此,研究近似解不僅具有理論價值,而且具有實際意義.QIU等[10?11]利用集值函數(shù)研究了向量優(yōu)化問題的近似解,同時得到了向量均衡問題近似弱有效解和近似Henig有效解的標(biāo)量化特征.
受以上研究的啟發(fā),我們在沒有任何凸性假設(shè)的情況下,利用非線性泛函討論近似Henig有效解的必要和充分最優(yōu)性條件.
2.預(yù)備知識

由文[7],我們得到泛函ξ的性質(zhì).
引理2.1若k ∈intC×intD,(y0,z0)∈Y×Z,則
(i)ξ(y,z) (ii)ξ(y,z)≤t ??(y,z)∈tk+(y0,z0)?cl(C×D); (iii)ξ(y,z)≥t ??(y,z)?tk+(y0,z0)?intC×intD; (iv)ξ(y,z)>t ??(y,z)?tk+(y0,z0)?cl(C×D); (v)ξ(y,z)=t ??(y,z)∈tk+(y0,z0)??C×?D; (vi)ξ是Y×Z上的嚴(yán)格C×D-單調(diào)連續(xù)凸泛函. 引理2.2若k ∈intC×intD,(y0,z0)∈Y×Z,則對任意的y ∈Y,z ∈Z,α ≥0有 ξ((y,z)?αk)=ξ(y,z)?α. 證對任意的y ∈Y,z ∈Z有 由引理2.2可得下面的推論. 推論2.1若k ∈intC×intD,(y0,z0)∈Y×Z,則對任意的y ∈Y,z ∈Z,下面結(jié)論成立 (i)ξ((y,z)+αk)=ξ(y,z)+α,?α ≥0; (ii)ξ((y,z)?αk)<ξ(y,z)<ξ((y,z)+αk),?α>0; (iii)ξ((y,z)+α1k)<ξ((y,z)+α2k),?α1<α2. 下證ψ(?ε,0)≥0.若t<0,則t(b0,d0)∈?intcone(B+U)×intD.由cone(B+U),D是點錐得(cone(B+U)×D)∩(?(intcone(B+U)×intD))=?,于是t(b0,d0)?cone(B+U)×D.因此,若t(b0,d0)∈cone(B+U)×D,則t ≥0.于是由(3.7)得ψ(?ε,0)≥0. 推論3.1設(shè)若是(Φ-SEPC)的一個Henig有效解,則存在Y×Z上正齊次次可加連續(xù)泛函ψ使得 證由D是凸錐得 推論3.2設(shè)B是C的基,ˉx ∈A.若存在Y×Z上正齊次次可加連續(xù)泛函ψ滿足 證由泛函ψ在Y×Z上的正齊次次可加連續(xù)性得ψ(0,0)=0.在定理3.2中令ε=0可以證得推論3.2成立. 在定理3.2中,泛函ψ在Y×Z上是正齊次次可加連續(xù)的.接下來,我們將減弱泛函ψ在Y×Z上的性質(zhì)得到下述定理. 定理3.3設(shè)ε ∈C,B是C的基,若存在Y×Z上泛函ψ滿足 證取一個零的均衡凸鄰域U2使得U2?VB.令U=U0∩U2,由(i)和(iii)得 推論3.3設(shè)B是C的基,ˉx ∈A.若存在Y×Z上泛函ψ滿足 (i) 存在零的鄰域U0?VB,若y1?y2∈intcone(B+U0),z1?z2∈D,則ψ(y1,z1)>ψ(y2,z2); (ii)ψ(y,z)≥0,?y ∈Φ(ˉx,x),z ∈G(x),x ∈X0; (iii)ψ(0,0)=0. 證在定理3.3中令ε=0可直接證得推論3.3成立. 本文中,我們引進(jìn)了帶約束集值均衡問題近似Henig有效解的概念.在沒有任何凸性假設(shè)下,利用非線性泛函建立了該解的必要和充分最優(yōu)性條件(見定理3.1和3.2),且該解的必要和充分條件在形式上大致統(tǒng)一,但在充分條件中要求泛函ψ在Y×Z上是正齊次次可加連續(xù)的,條件較強(qiáng).于是,我們減弱泛函的性質(zhì)建立了該解的另一充分最優(yōu)性條件(見定理3.3).最后,我們在上述基礎(chǔ)上建立了帶約束集值均衡問題Henig有效解最優(yōu)性條件.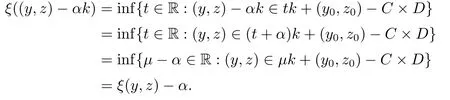

3.帶約束集值均衡問題的最優(yōu)性條件







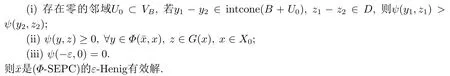
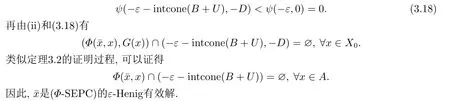
4.結(jié)論

