馬云真, 孫忱, 李江華, 牛旭君

(1.西安理工大學(xué)理學(xué)院,陜西 西安 710058,2.武警工程大學(xué)理學(xué)院,陜西 西安 710086)

馬云真1, 孫忱1, 李江華1, 牛旭君2

(1.西安理工大學(xué)理學(xué)院,陜西 西安 710058,2.武警工程大學(xué)理學(xué)院,陜西 西安 710086)

利用初等和解析方法研究了F.Smarandache LCM函數(shù)與數(shù)論函數(shù)(n)的混合均值分布問題,獲得了一些較強(qiáng)的漸近公式,發(fā)展豐富了數(shù)論領(lǐng)域里相關(guān)研究工作.

F.Smarandache LCM函數(shù);數(shù)論函數(shù)(n);均值;漸近公式

1 引言及結(jié)論

F.Smarandache LCM 函數(shù)[1]:SL(1)=1,當(dāng) n＞1且為n的標(biāo)準(zhǔn)分解式時(shí),有

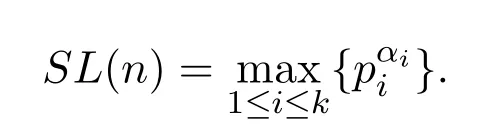
函數(shù)(n):(1)=1,當(dāng)n＞1且為n的標(biāo)準(zhǔn)分解式時(shí),有

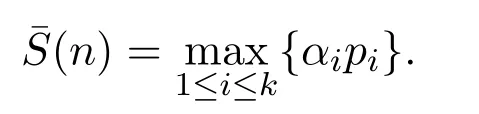
對(duì)任意實(shí)數(shù)x＞1,有

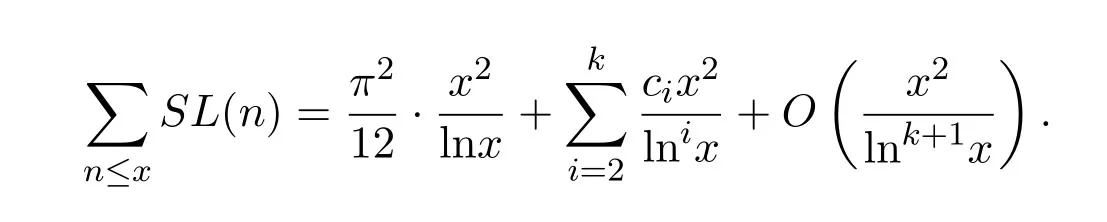
其中 ci(i=2,3,···,k)為可計(jì)算常數(shù).

在文獻(xiàn)[3]中魯偉陽和高麗研究了Smarandache LCM函數(shù)與數(shù)論函數(shù)(n)的高次混合均值問題,即就是證明了下面的定理:對(duì)任意實(shí)數(shù)x＞1,有

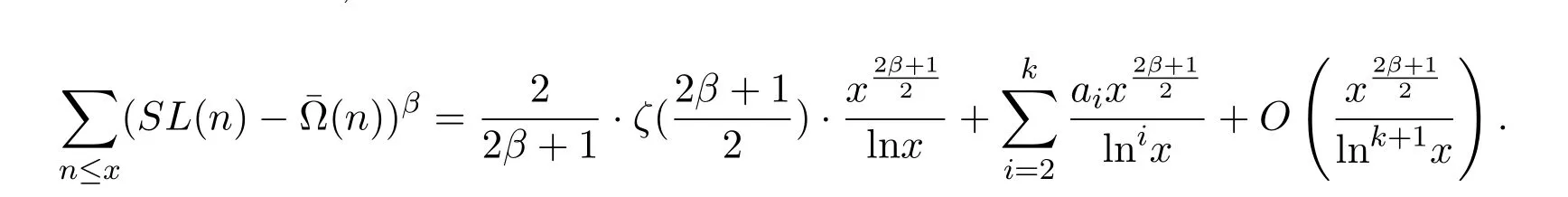
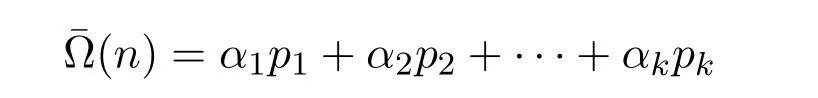
ζ(s)為 Riemann zeta函數(shù),β＞1,ai(i=2,3,···,k)為可計(jì)算常數(shù).

對(duì)任意實(shí)數(shù)x＞1,有

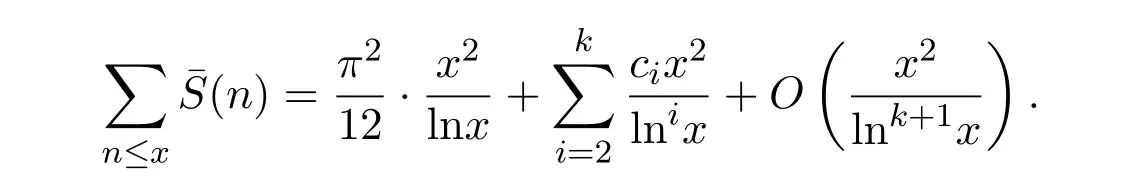
其中 ci(i=2,3,···,k)為可計(jì)算常數(shù).

設(shè)P(n)表示n的最大素因子,則對(duì)任意實(shí)數(shù)x＞1,有漸近公式

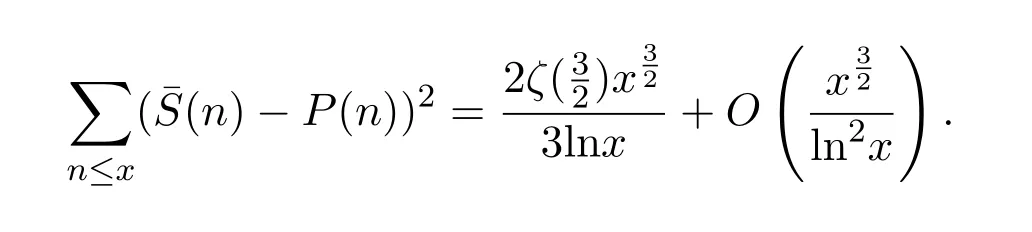
其中 ζ(s)為Riemann zeta函數(shù).

(1)設(shè)k為任意正整數(shù),那么對(duì)任意實(shí)數(shù)x＞1,有漸近公式

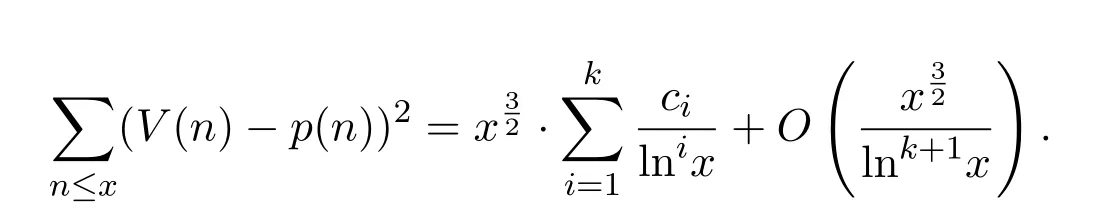
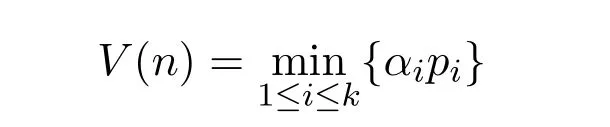
p(n)表示n的最小素因子,ci(i=2,3,···,k)為可計(jì)算常數(shù)且

(2)設(shè)k為任意正整數(shù),那么對(duì)任意實(shí)數(shù)x＞1,有漸近公式

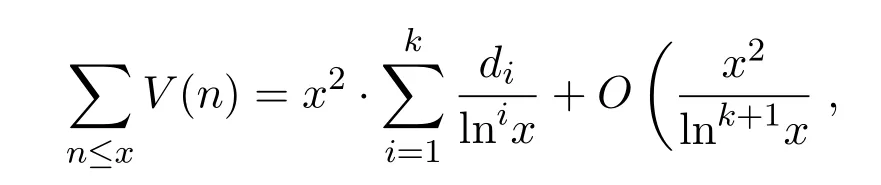
其中 di(i=2,3,···,k)為可計(jì)算常數(shù)且

本文的主要是利用初等和解析方法研究F.Smarandache LCM函數(shù)與數(shù)論函數(shù)(n)的混合均值問題,并給出幾個(gè)較強(qiáng)的漸近公式.具體地說也就是證明下面:

定理 1.1對(duì)任意實(shí)數(shù)x＞1,有漸近公式

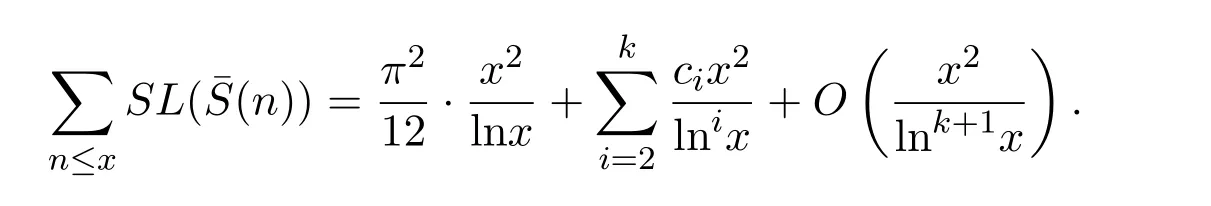
其中 ci(i=2,3,···,k)為可計(jì)算常數(shù).

定理 1.2對(duì)任意實(shí)數(shù)x＞1,有漸近公式

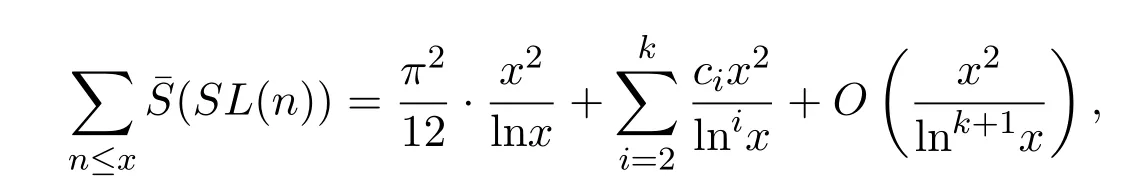
其中 ci(i=2,3,···,k)為可計(jì)算常數(shù).

定理 1.3對(duì)任意實(shí)數(shù)x＞1,α≥0,有漸近公式

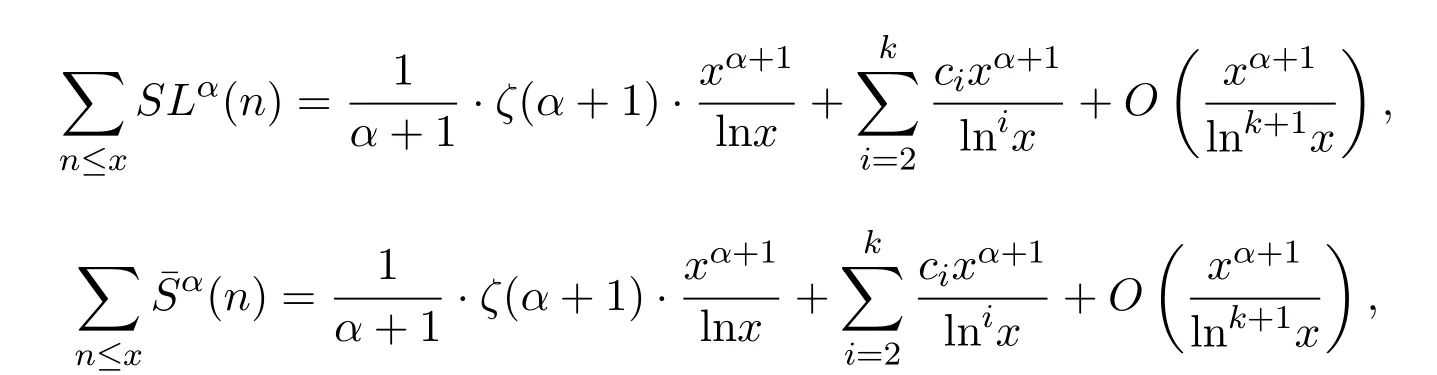
其中 ζ(s)為 Riemann zeta函數(shù),ci(i=2,3,···,k)為可計(jì)算常數(shù).

定理 1.4對(duì)任意實(shí)數(shù)x＞1,α≥0,β≥0,有漸近公式

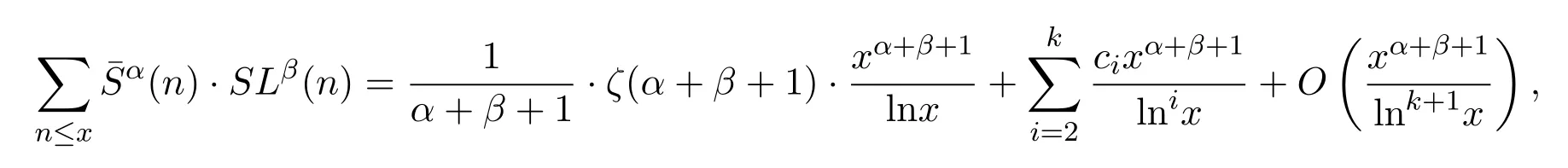
其中 ζ(s)為 Riemann zeta函數(shù),ci(i=2,3,···,k)為可計(jì)算常數(shù).

定理 1.5對(duì)任意實(shí)數(shù)x＞1,α＞0,有漸近公式

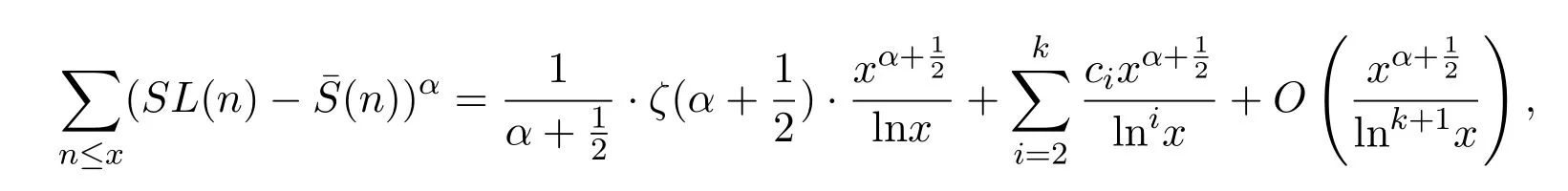
其中 ζ(s)為 Riemann zeta函數(shù),ci(i=2,3,···,k)為可計(jì)算常數(shù).

定理1.6對(duì)任意正整數(shù)n,函數(shù)SL(n)和函數(shù)(n)有

2 引理

為了完成定理的證明,首先需要如下兩個(gè)簡(jiǎn)單的引理.

引理 2.1[9]對(duì)任意實(shí)數(shù)x＞1,有漸近公式

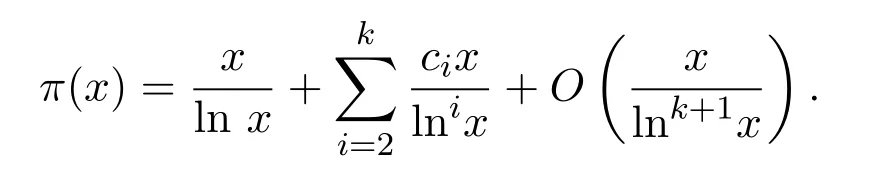
其中 ci(i=2,3,···,k)為可計(jì)算常數(shù).

引理 2.2[10]設(shè) b(n)(n=1,2,···)是一復(fù)數(shù)列,其和函數(shù)

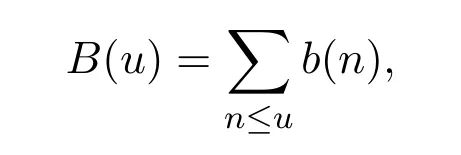
再設(shè)0≤u1＜u2,f(n)是[u1,u2]上的連續(xù)可微函數(shù),那么有

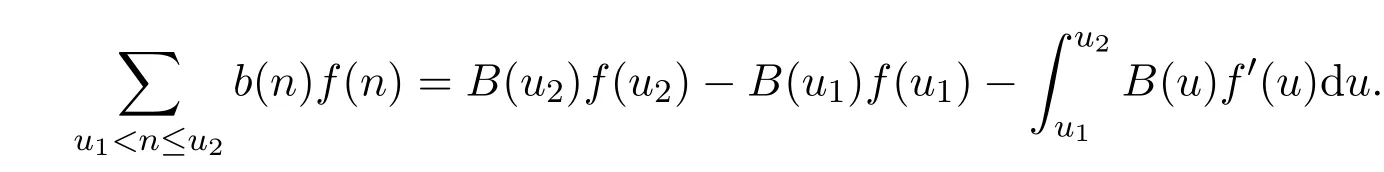
引理 2.3[10]對(duì)任意實(shí)數(shù)x＞1,有漸近公式

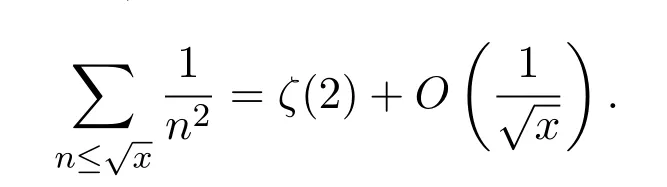
其中 ζ(s)為Riemann zeta函數(shù).

引理的詳細(xì)證明參見文獻(xiàn)[9-10].

3 定理的證明

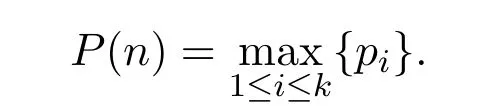
證明定義如下兩個(gè)集合A和B:

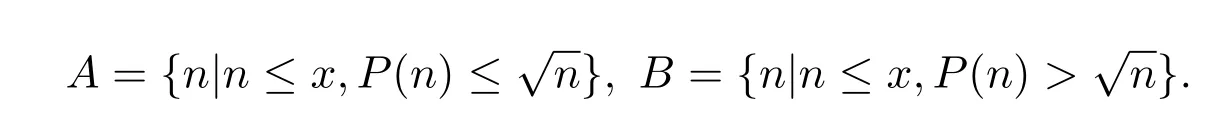
則對(duì)定理1.1,

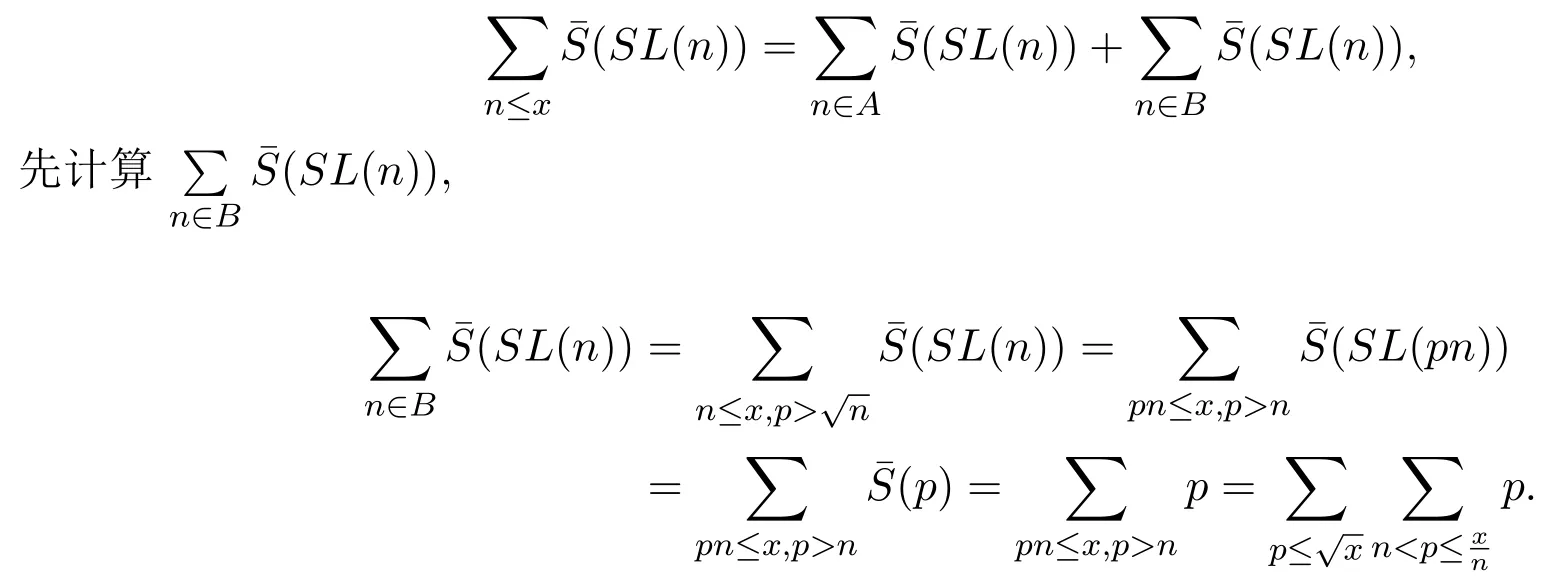
利用引理2.1-引理2.3可知,

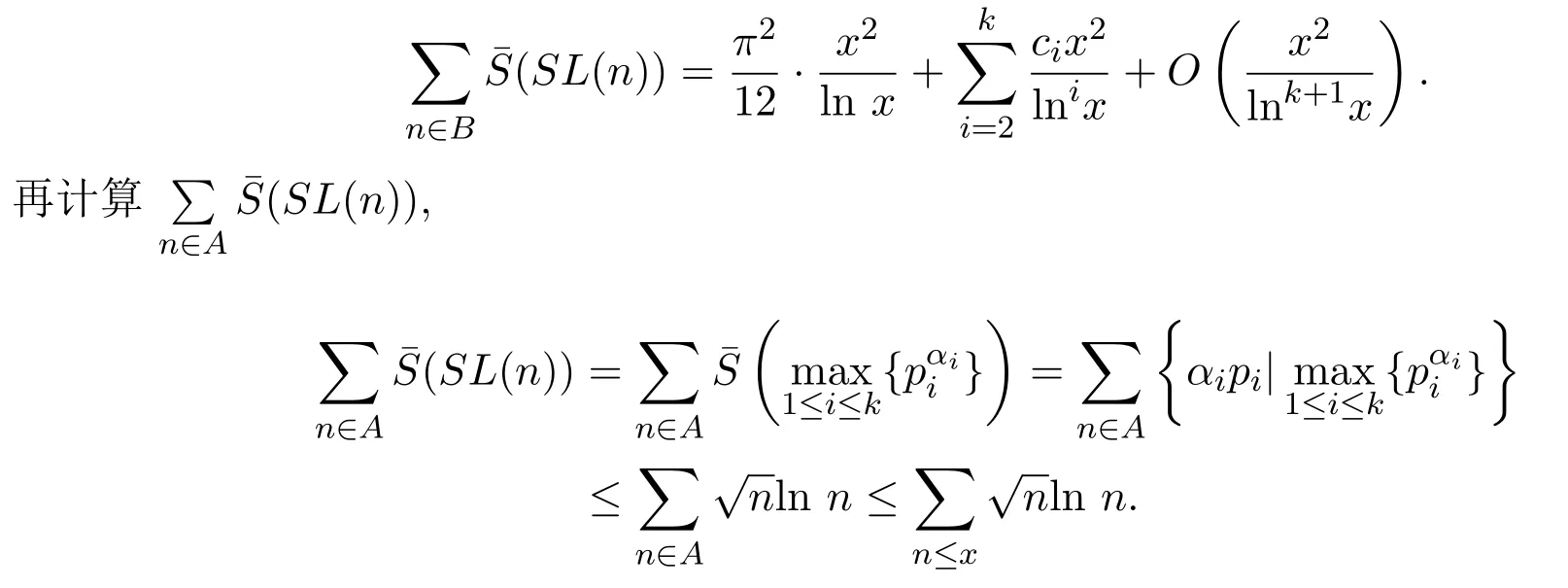
應(yīng)用Euler求和公式[10],可得

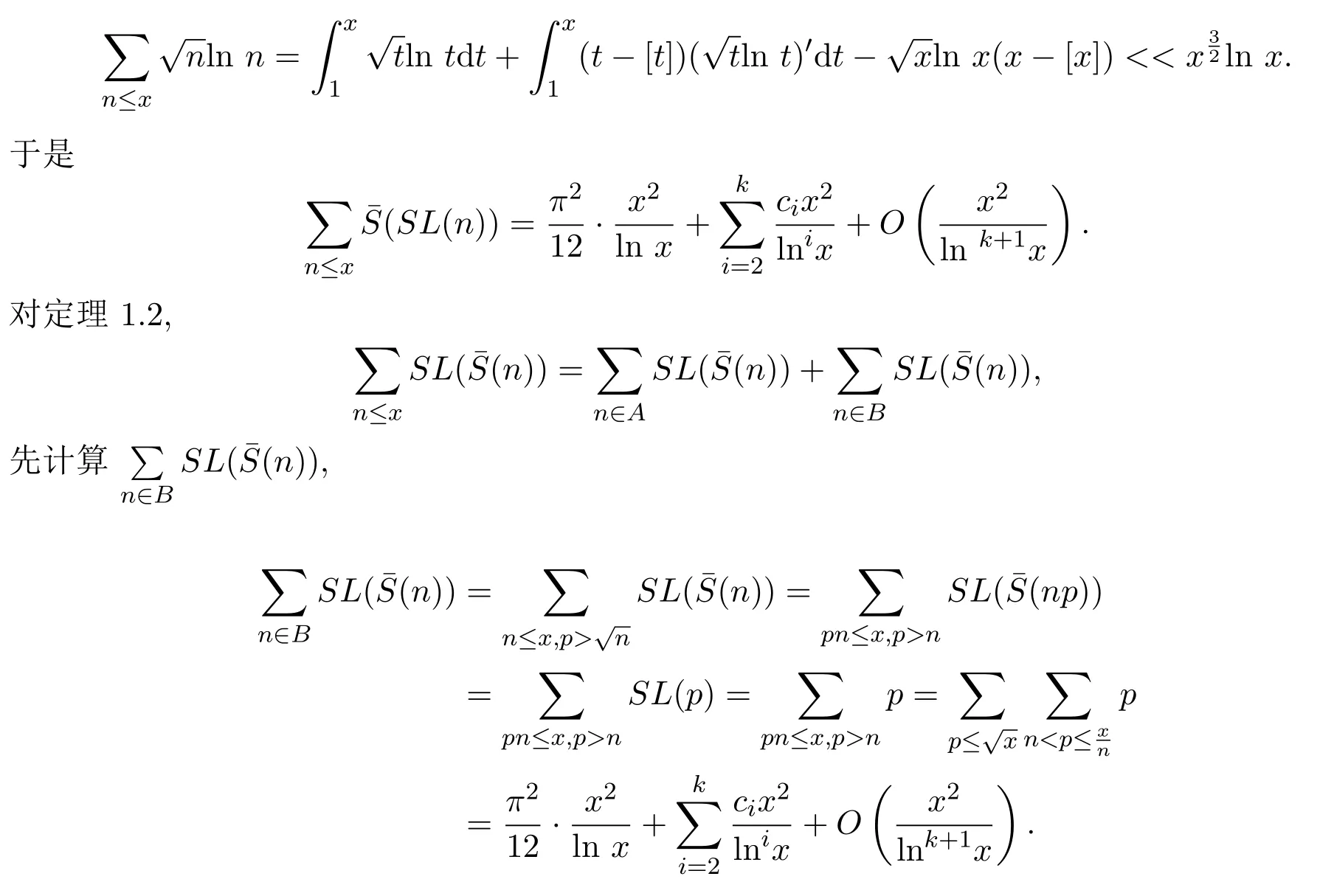
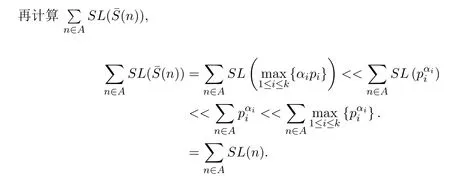
利用文獻(xiàn)[2]中的方法,可知 ∑

對(duì)于定理1.5,利用文獻(xiàn)[8]中的方法,將正整數(shù)集合N 劃分成以下5個(gè)子集合A′,B′,C′,D′,E′.即

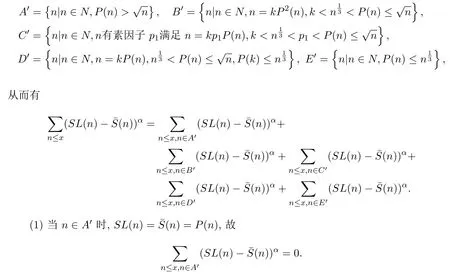
(2)當(dāng)n∈B′時(shí),SL(n)=P2(n),(n)=2P(n),故

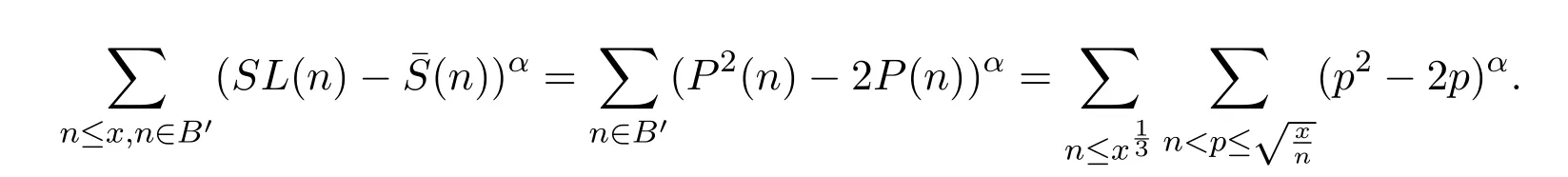
利用引理2.1-引理2.3可知,

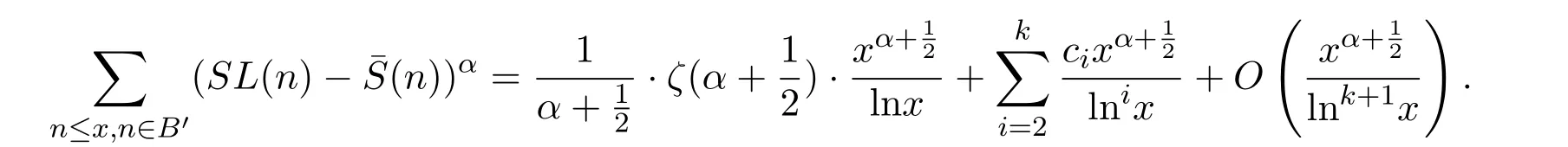
(3)當(dāng)n∈C′時(shí),SL(n)=(n)=P(n),故

(4)當(dāng)n∈D′時(shí),任意正整數(shù)a和素?cái)?shù)p有ap≤pa成立,參考文獻(xiàn)[8]中的方法,故

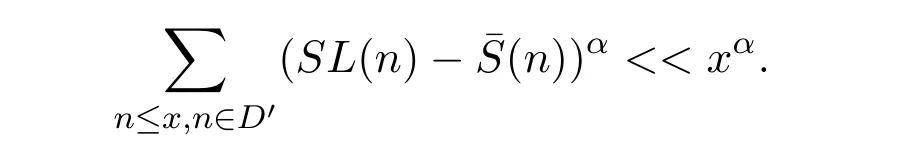
(5)當(dāng) n ∈E′時(shí),有.如果SL(n)=P(n),那么(n)=P(n).利用文獻(xiàn)[8]中的方法,有

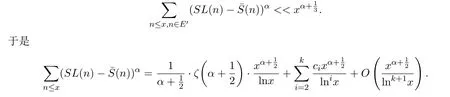
對(duì)于定理1.6,(1)-(4)顯然,然而對(duì)(5),令θ(n)表示(n)迭代使函數(shù)值不變的最小次數(shù).

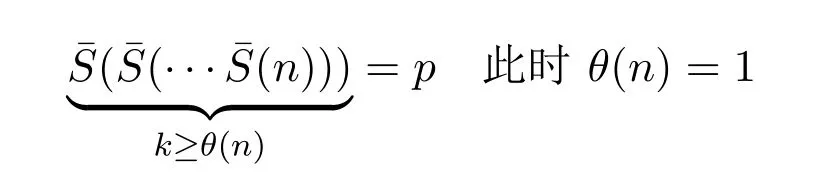
(b)當(dāng)n∈B 時(shí),有

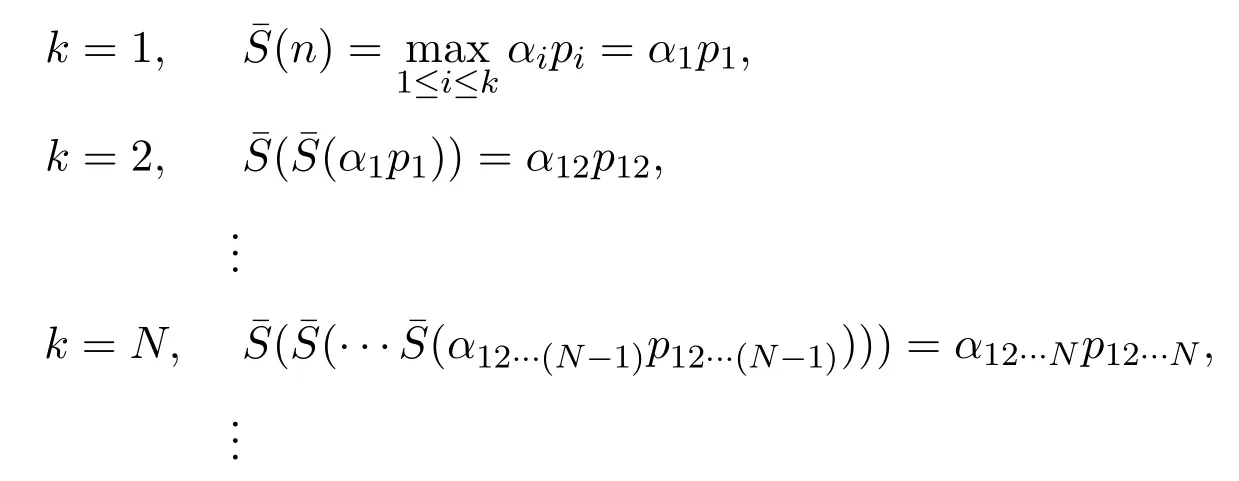
假設(shè)存在正整數(shù) k 使得 α12···k ≤ p12···k 則

若對(duì)所有的正整數(shù) k 有 α12···k＞ p12···k,則數(shù)列

嚴(yán)格遞減,于是必存在正整數(shù) k0 使得 α12···k0≤ p12···k0,即有

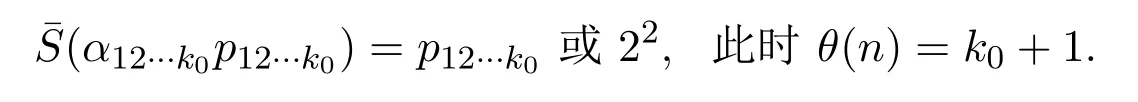
所以不可能對(duì)所有的正整數(shù) k 有 α12···k＞ p12···k成立,定理 1.6 得證!

綜上所述,所有定理得到了證明.

致謝：衷心地感謝王尚平教授的支持和鼓勵(lì)！

[1]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993.

[2]Lü Zhongtian.On the F.Smarandache LCM function and its mean value[J].Scientia Magna,2007,3(1):22-25.

[3]魯偉陽,高麗.Smarandache LCM函數(shù)與數(shù)論函數(shù)?(n)的高次混合均值[J].延安大學(xué)學(xué)報(bào):自然科學(xué)版,2017,36(1):13-15.

[4]Ma Jinping.The Smarandache multiplicative function[J].Scientia Magna.,2006,1(1):125-128．

[5]徐哲峰.Smarandache函數(shù)的值分布性質(zhì)[J].數(shù)學(xué)學(xué)報(bào),2006,49(5):1009-1012.

[6]沈虹.一個(gè)新的數(shù)論函數(shù)及其它的值分布[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2007,23(2):235-238.

[7]張利霞,趙西卿,郭瑞,等.關(guān)于數(shù)論函數(shù)S(SL(n))=φ(n)的可解性[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2015,31(5):533-536.

[8]楊衍婷,任剛練.關(guān)于Smarandache LCM函數(shù)和Smarandache函數(shù)SM(n)的混合均值[J].黑龍江大學(xué)自然科學(xué)學(xué)報(bào),2013,30(3):318-320.

[9]Tom M Apostol.Introduction to Analytic Number Theory[M].New York:Springer-Verlag,1976.

[10]潘承洞,潘承彪.解析數(shù)論[M].北京:科學(xué)出版社,1999.

On the hybrid mean value of Smarandache LCM function and Smarandache function(n)

Ma Yunzhen1,Sun Chen1,Li Jianghua1,Niu Xujun2
(1.Faculty of Siciences,Xi′an University of Technology,Xi′an 710058,China;2.Faculty of Sciences,CAPF of Engineering University,Xi′an 710086,China)

Using the elementary and analytic methods to study the F.Smarandache LCM function and arithmetical function(n)hybrid mean value problem,some asymptotic formulas are given,it has developed and enriched the relevant research work in the fi eld of number theory.

F.Smarandache LCM function,arithmetical function(n),mean value,asymptotic formula

O156.4

A

1008-5513(2017)05-0522-08

10.3969/j.issn.1008-5513.2017.05.010

2017-09-12.

陜西省自然科學(xué)基金(2017JQ1020).

馬云真(1989-),碩士生,研究方向:解析數(shù)論及其應(yīng)用.

李江華,博士,副教授,研究方向:解析數(shù)論及其應(yīng)用.

2010 MSC:11B83