基于廣義Logistic模型的美國(guó)白蛾優(yōu)化控制策略
張巧玲, 陸海霞*, 張 翼
(1. 宿遷學(xué)院文理學(xué)院, 江蘇 宿遷 223800; 2. 沈陽(yáng)工業(yè)大學(xué)理學(xué)院, 沈陽(yáng) 110870)
1 預(yù)備知識(shí)
本文在描述美國(guó)白蛾種群密度時(shí), 將模型dN/dt=rN(1-N/K)p中的調(diào)整系數(shù)p取為3.基于美國(guó)白蛾繁殖規(guī)律,考慮到對(duì)美國(guó)白蛾的捕獲努力量, 則美國(guó)白蛾種群可描述為
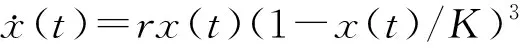
(1)
其中x(t)為t時(shí)刻美國(guó)白蛾種群的密度.不失一般性, 所有參數(shù)均為正值.
2 主要結(jié)果
2.1 平衡點(diǎn)的存在性及穩(wěn)定性
模型(1)所描述的美國(guó)白蛾種群密度增長(zhǎng)速度如圖1所示.從圖1可以看出, 只有當(dāng)美國(guó)白蛾負(fù)增長(zhǎng)時(shí), 外來(lái)物種對(duì)環(huán)境的影響才會(huì)減弱.當(dāng)美國(guó)白蛾負(fù)增長(zhǎng)時(shí), 其種群密度已超過(guò)環(huán)境的最大容納量K, 打破原有平衡, 故考慮捕獲努力量E.設(shè)捕獲函數(shù)h(x)正比于種群密度和捕獲努力量的乘積, 即h(x)=qEx(t), 其中捕獲能力系數(shù)q>0, 則美國(guó)白蛾種群密度可描述為
(2)
引理1若系統(tǒng)(2)中參數(shù)均為正常數(shù), 且滿(mǎn)足r>qE, 令x(t)為系統(tǒng)(2)的平衡點(diǎn), 則對(duì)所有t≥0, 系統(tǒng)(2)的平衡點(diǎn)在[0,+∞)上.
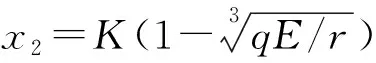
系統(tǒng)(2)的平衡點(diǎn)是直線(xiàn)y=h(x)與曲線(xiàn)y=f(x)的交點(diǎn)(見(jiàn)圖2), 即方程rx(1-x/K)3-qEx=0.由于其導(dǎo)數(shù)為r(1-x/K)2(1-4x/K)-qE, 易證:
定理2x=0是系統(tǒng)(2)的平衡點(diǎn),且當(dāng)r>qE時(shí), 系統(tǒng)不穩(wěn)定.
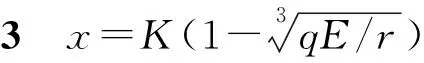
2.2 種群動(dòng)力學(xué)性質(zhì)
圖2為不同情況下系統(tǒng)(2)的平衡點(diǎn)位置.圖2(a)顯示, 當(dāng)y=h(x)與y=f(x)有唯一交點(diǎn)x=0時(shí), 比較2條曲線(xiàn)在原點(diǎn)的斜率可知, 此時(shí)qE=r,說(shuō)明當(dāng)線(xiàn)性捕獲系數(shù)達(dá)到其內(nèi)稟增長(zhǎng)率時(shí), 美國(guó)白蛾的種群密度可控制為零.圖2(b)顯示, 此時(shí)y=h(x)與y=f(x)也是只有唯一交點(diǎn)x=0, 比較兩條曲線(xiàn)在原點(diǎn)的斜率可知, 此時(shí)qE>r, 說(shuō)明美國(guó)白蛾的入侵得到了有效控制, 防治和捕殺工作效果顯著, 顯然這個(gè)階段的狀態(tài)不會(huì)持續(xù)很久就會(huì)趨向于圖2(a)的狀態(tài).圖2(c)顯示, 當(dāng)y=h(x)與y=f(x)有正交點(diǎn)x*時(shí), 由2條曲線(xiàn)在交點(diǎn)前的斜率可知, 美國(guó)白蛾種群密度的增長(zhǎng)率先增后減, 得到了有效的抑制作用, 此時(shí)qE 定理4在D中使得H(E)取得最大值的最優(yōu)捕獲努力量E*=27r/(64q), 相應(yīng)的最大捕獲量H*(E*)=27Kr/256, 優(yōu)化控制的美國(guó)白蛾密度x*(E*)=K/4. 本文基于廣義Logistic模型, 研究了美國(guó)白蛾繁殖速度與捕獲系統(tǒng)的動(dòng)力學(xué)性質(zhì),分析了平衡點(diǎn)及其系統(tǒng)處于穩(wěn)定狀態(tài)的充分條件, 并給出了在正平衡點(diǎn)處可持續(xù)發(fā)展的最大捕獲努力量E*=27r/(64q), 使美國(guó)白蛾的種群密度控制為最大容納量的1/4.2.3 美國(guó)白蛾的優(yōu)化控制
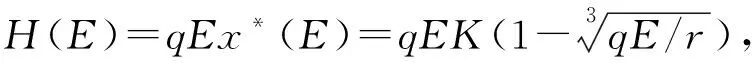
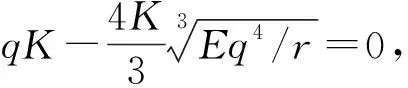
3 結(jié)論
 揚(yáng)州大學(xué)學(xué)報(bào)(自然科學(xué)版)2020年4期
揚(yáng)州大學(xué)學(xué)報(bào)(自然科學(xué)版)2020年4期
- 揚(yáng)州大學(xué)學(xué)報(bào)(自然科學(xué)版)的其它文章
- 基于MHI的三重運(yùn)動(dòng)表現(xiàn)人體動(dòng)作圖像識(shí)別方法
- 自適應(yīng)事件觸發(fā)NCS魯棒容錯(cuò)控制與通訊協(xié)同設(shè)計(jì)
- 基于非線(xiàn)性累積損傷理論與沖擊模型的疲勞壽命預(yù)測(cè)
- 分?jǐn)?shù)階q-差分方程多點(diǎn)邊值問(wèn)題解的存在性與唯一性
- RN空間中一類(lèi)非線(xiàn)性彈性波導(dǎo)方程解的特點(diǎn)
- 三種群捕食系統(tǒng)動(dòng)力行為與最優(yōu)捕獲策略
