周 瑜, 寇 綱, 白 楊, 爾古打機

(1.內(nèi)蒙古大學(xué)經(jīng)濟管理學(xué)院,內(nèi)蒙古自治區(qū)呼和浩特010021;2.西南財經(jīng)大學(xué)工商管理學(xué)院,四川成都611130;3.西南民族大學(xué)電氣信息工程學(xué)院,四川成都610041)

1 引 言

生產(chǎn)設(shè)備是企業(yè)的重要資產(chǎn),生產(chǎn)設(shè)備的運行狀況嚴(yán)重影響企業(yè)的生產(chǎn)安全和效率.企業(yè)為了提高生產(chǎn)設(shè)備的可用度,通常對設(shè)備實施一系列的預(yù)防維修政策.據(jù)文獻[1,2]統(tǒng)計,設(shè)備維修費用一般占全部生產(chǎn)成本的15%～70%,平均為20.8%.發(fā)達國家交通運輸行業(yè)的數(shù)據(jù)為20%～30%,鋼鐵行業(yè)約為40%.同時,預(yù)防維修質(zhì)量與預(yù)防維修成本之間具有一定的內(nèi)在關(guān)系[3].因此,如何獲得最優(yōu)的預(yù)防維修質(zhì)量一直是研究熱點.

對于預(yù)防維修,設(shè)備經(jīng)歷一次預(yù)防維修后,設(shè)備的失效強度與預(yù)防維修之前相比通常會出現(xiàn)以下五種情形: 比新的好(better than new,BTN),修復(fù)如新(as good as new,AGAN),介于新舊之間(worse than new but better than old,WNBO),修復(fù)如舊(as bad as old,ABAO)和比舊的差(worse than old,WTO).其中BTN 意味著設(shè)備經(jīng)歷一次預(yù)防維修后,它的失效強度明顯優(yōu)于預(yù)防維修之前,即出現(xiàn)了可靠性增長現(xiàn)象[4,5].此狀態(tài)下的常見模型為可靠性增長模型[4,5].然而,可靠性增長現(xiàn)象很難出現(xiàn)在劣化系統(tǒng)中.AGAN意味著設(shè)備的失效強度在預(yù)防維修后恢復(fù)到新設(shè)備的水平,即設(shè)備的狀態(tài)完好如新.這種狀態(tài)在電子元器件的可靠性建模中較為常見,常用的建模方法為更新過程[6,7].ABAO 表示設(shè)備的失效強度在預(yù)防維修前后無差異,即設(shè)備的狀態(tài)恢復(fù)如舊.由于這種狀態(tài)假設(shè)既不影響失效強度的變化趨勢也不影響失效強度的變化速率,因此在設(shè)備可靠性建模中最為常見,常用的建模方法有點過程模型[8].實際上,設(shè)備經(jīng)歷一次預(yù)防維修后,其失效強度一般會介于新舊狀態(tài)之間,即WNBO 狀態(tài),也稱之為不完美維修[9].針對WNBO 狀態(tài),Wang 等[10]總結(jié)了已有建模方法,讀者可以通過該文獻進一步了解這些方法.WTO 狀態(tài)是五種維修狀態(tài)中最不理想的一種狀態(tài).WTO 狀態(tài)意味著設(shè)備在執(zhí)行預(yù)防維修后,設(shè)備的失效強度較預(yù)防維修之前相比出現(xiàn)明顯的劣化趨勢.

以上五種情形中,關(guān)于不完美維修的應(yīng)用和研究最常見,現(xiàn)有文獻開發(fā)了許多經(jīng)典模型,如Kijima 模型[11,12],BP 模型[13]等.Wu 等[14]把這些方法大致劃分為三類,分別是年齡減模型,失效強度減模型和混合模型.基于本文模型應(yīng)用的背景,本文僅就失效強度減模型進行討論.失效強度減模型通常假設(shè)設(shè)備經(jīng)歷一次預(yù)防維修后,設(shè)備的失效強度將減少一確定值或與原失效強度成固定比例的減少.已有研究中,有大量的關(guān)于失效強度減的文獻,如文獻[15–21].Nakagawa 等[18?21]提出的失效強度減模型就是成比例減少模型,即假設(shè)預(yù)防維修后的設(shè)備失效強度減少量與預(yù)防維修前的失效強度成一定比例.Wu 等[22]建議的模型則是假設(shè)預(yù)防維修后的設(shè)備失效強度將隨機減少一定量值.隨后,算術(shù)失效強度減(Arithmetic Reduction of Intensity,ARI)模型被廣泛應(yīng)用[15?17,19,20].文獻[16]在Nakagawa 等的模型基礎(chǔ)上提出了一個p階記憶模型,其中階數(shù)p是指預(yù)防維修能夠影響到的未來預(yù)防維修區(qū)間數(shù).而Chan 等的模型實質(zhì)上就是一種無限記憶模型.Toledo 等[17]隨后給出了p階記憶模型的極大似然估計方法和模型選擇方法.Zhou 等[23]根據(jù)實際應(yīng)用背景,提出了一個新的算術(shù)失效強度減模型.該模型假設(shè)設(shè)備經(jīng)歷一次預(yù)防維修后的失效強度等于預(yù)防維修前的失效強度和一個當(dāng)量之和.這個當(dāng)量與預(yù)防維修前的失效強度和設(shè)備固有失效強度之差成一定比例,進而采用該比例描述設(shè)備預(yù)防維修質(zhì)量.通過與現(xiàn)有模型的比較說明了方法的有效性.

在上述模型和方法中, 通常假設(shè)設(shè)備的失效強度的變化是平滑的.現(xiàn)實中, 設(shè)備的失效強度有可能在某一時間區(qū)間上出現(xiàn)失效強度變化趨勢不一致的情形, 這種現(xiàn)象被稱為失效變點[24].基于此, 本文在Zhou 等[23]的工作基礎(chǔ)上,給出了一個具有失效變點的算術(shù)強度減模型.

2 變點–算術(shù)失效強度減模型

生產(chǎn)設(shè)備通常具有多個不同時間周期的預(yù)防維修,簡稱為多級預(yù)防維修制度.以巴士車隊為例,每隔15天進行一次一級預(yù)防維修;每隔3 個月～4 個月進行一次二級預(yù)防維修;每隔2年進行一次高級預(yù)防維修.為了模型構(gòu)建過程的簡捷,接下來將以具有二級預(yù)防維修制度的設(shè)備為例進行說明,但這并不影響該模型擴展到更多級別的預(yù)防維修制度.具有二級預(yù)防維修制度的設(shè)備發(fā)生故障和維修歷程如圖1 所示.在圖1中,車隊在171 周內(nèi)共進行了7 次二級預(yù)防維修.例如,車隊在第26 周,第48 周做了第1 次,第2 次預(yù)防維修.假設(shè)一次預(yù)防維修結(jié)束后,重新計算車隊在該預(yù)防維修區(qū)間內(nèi)的失效表現(xiàn),直到下一次預(yù)防維修來臨為止.因此,車隊的第1 個預(yù)防維修影響下的車隊失效表現(xiàn)區(qū)間為[0,22].由圖可以看出,車隊預(yù)防維修的執(zhí)行并非嚴(yán)格按等周期進行,即預(yù)防維修周期是非齊次的.本文采用累積失效次數(shù)衡量車隊失效表現(xiàn),圖中每一段帶圈實線表示在上一次二級預(yù)防維修后和下一次二級預(yù)防維修之前,車隊發(fā)生失效的累積次數(shù).圖線斜率越大,說明該二級預(yù)防維修區(qū)間內(nèi)車隊失效越頻繁.

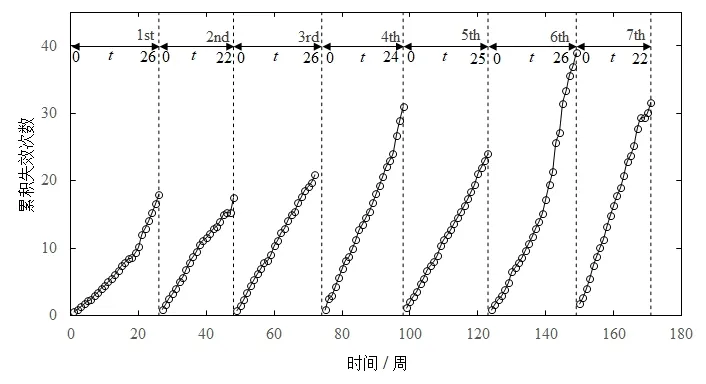
圖1 設(shè)備故障和維修歷程Fig.1 Equipment failure and maintenance process

根據(jù)圖1,車隊在第123 周進行了第五次二級預(yù)防維修.此后,車隊的失效頻率出現(xiàn)了較為明顯的變化,在該二級預(yù)防維修區(qū)間內(nèi)的累積失效次數(shù)高達39 次,遠(yuǎn)高于其它二級預(yù)防維修區(qū)間.實際上,引起該變化的原因是車隊在該區(qū)間內(nèi)發(fā)生了營運線路的變更.線路變更引起了失效頻率的變化,這種變化可以看作為失效變點[24].如果不考慮變點的存在,建模得到的結(jié)果可能存在一定偏差.因此,本文將基于以下假設(shè)構(gòu)建失效變點–算術(shù)失效強度減模型.

2.1 模型假設(shè)

具有二級預(yù)防維修制度的設(shè)備預(yù)防維修歷程如圖2 所示.

圖2 設(shè)備二級預(yù)防維修歷程Fig.2 Equipment type-II preventive maintenance process

根據(jù)圖2, 假設(shè)設(shè)備進行第i次二級預(yù)防維修的時間為Ti,i= 1,2,...,n.假設(shè)二級預(yù)防維修為等周期預(yù)防維修, 則有T1=T2?T1=···=Tn ?Tn?1.在第i個二級預(yù)防維修周期內(nèi), 設(shè)備進行第j次一級預(yù)防維修的時間為Hj,j= 1,2,...,mi.且有H1=H2?H1=···=Hmi ?Hmi?1和Ti ?Ti?1= (mi+1)(Hmi ?Hmi?1)成立.令t為任意一個一級預(yù)防維修周期內(nèi)的運行時間, 為一非負(fù)變量, 0 ≤t≤Hmi ?Hmi?1.假設(shè)在t時間內(nèi)每隔Δt統(tǒng)計一次系統(tǒng)的累積失效次數(shù), 觀察時間點可簡記為tpj(t=pjΔt),且令Mji(t)標(biāo)識觀察到的累積失效次數(shù),即令Mji(t)標(biāo)記第j次和第j+1次一級預(yù)防維修區(qū)間內(nèi)的累積失效次數(shù).經(jīng)歷一次一級預(yù)防維修后,Mj i(t)清零并重新計算.這樣,獲得的失效觀察次數(shù),如表1 所示.由于實際執(zhí)行過程中,預(yù)防維修區(qū)間非嚴(yán)格相等,因此出現(xiàn)觀察時間點非齊次現(xiàn)象.例如,表1的[H2,H3]區(qū)間內(nèi),tpj中的累積失效次數(shù)為null,意味著設(shè)備在tpj來臨前已經(jīng)進行了預(yù)防維修.

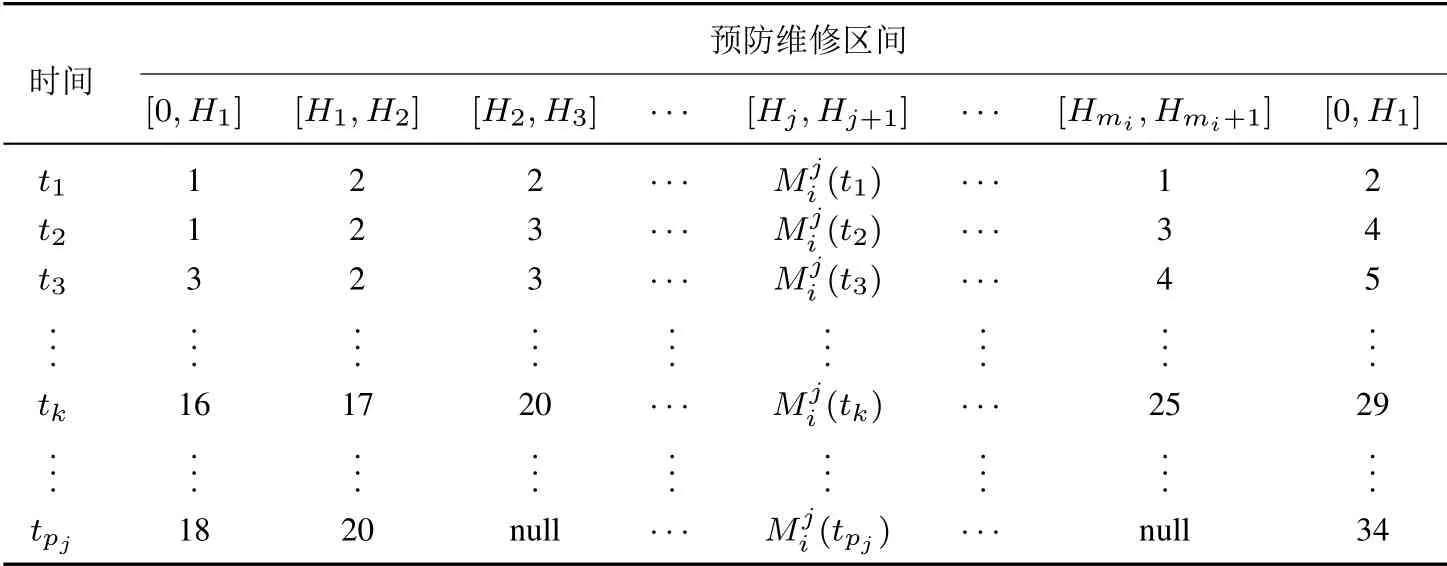
表1 累積失效次數(shù)Table 1 Cumulative failure number

此外,令(t)標(biāo)識設(shè)備在第i次二級預(yù)防維修區(qū)間內(nèi)進行的第j次一級預(yù)防維修區(qū)間內(nèi)的實際失效強度,而設(shè)備的固有失效強度記為(t).假設(shè)設(shè)備的預(yù)防維修質(zhì)量為變量,令ρi為第i次二級預(yù)防維修質(zhì)量,為第i次二級預(yù)防維修區(qū)間內(nèi)第j次一級預(yù)防維修質(zhì)量.冪律模型的參數(shù)為αi和βi.為了方便建模,結(jié)合文獻[23],還對模型做如下假設(shè):

1)設(shè)備故障修理時間,預(yù)防維修時間和停機時間與設(shè)備的運行時間相比足夠小,可以忽略不計.

2)設(shè)備故障修理因為是最小維修,因此故障修理不會本質(zhì)上改變設(shè)備的固有失效強度.因此,在對設(shè)備失效強度進行建模時可以應(yīng)用失效計數(shù)過程.

3)固有失效強度一般可以由進行首次預(yù)防維修前的失效歷程進行確定.實際上,設(shè)備首次進行預(yù)防維修前的失效歷程很難獲得,即使獲得也很難推斷出失效的固有失效強度.因此,如果無法獲得首次預(yù)防維修前的失效歷程,可以將能夠獲得的最早失效歷程作為建模固有失效強度的參考.

2.2 模型構(gòu)建

根據(jù)以上假設(shè),令設(shè)備經(jīng)歷一次預(yù)防維修后的失效強度等于預(yù)防維修前的失效強度和一個當(dāng)量之和.文獻[20]中假設(shè)該當(dāng)量與預(yù)防維修前的失效強度和預(yù)測失效強度之差成一定比例,失效強度僅基于最近的預(yù)防維修區(qū)間的失效強度進行預(yù)測.由于失效強度的變化受過去所有預(yù)防維修和固有失效強度的累積影響,文獻[23]在此基礎(chǔ)上提出,該當(dāng)量與預(yù)防維修前的失效強度和設(shè)備固有失效強度之差成一定比例.因此,第i次二級預(yù)防維修區(qū)間內(nèi)第j次一級預(yù)防維修后的失效強度之和.

第i次二級預(yù)防維修區(qū)間內(nèi)第1 次一級預(yù)防維修前的失效強度只受第i次二級預(yù)防維修影響,因此第i次二級預(yù)防維修區(qū)間內(nèi)第1 次一級預(yù)防維修前的失效強度可以表達為之和.綜上所述,可以得到不含有失效變點的算術(shù)失效強度減模型[23]

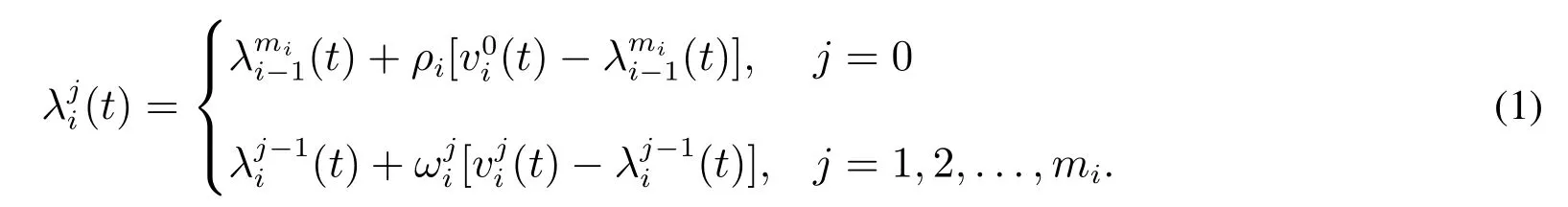
當(dāng)i= 1,2,...,n時,上式成立.當(dāng)i= 0 時(即無任何預(yù)防維修干擾時),根據(jù)假設(shè)3)和圖2 有(t) =(t).

如果設(shè)備的運營環(huán)境,工作強度等在第i次二級預(yù)防維修區(qū)間的第j次一級預(yù)防維修后發(fā)生較大變化,從而使得設(shè)備的失效強度變化趨勢發(fā)生變化,已有文獻稱之為失效變點[23].設(shè)備失效強度的趨勢變化通常表現(xiàn)為短周期內(nèi)兩次相鄰失效的時間間隔變化和長周期的趨勢變化.對于短周期內(nèi)的失效時間間隔變化可以引入一個尺度參數(shù)描述,而長周期的趨勢變化可以引入一個形狀參數(shù)進行度量.在現(xiàn)有失效強度模型中兩參數(shù)冪律模型恰好含有一個尺度參數(shù)和一個形狀參數(shù),因此本文采用冪律模型對失效趨勢進行平滑處理.平滑處理的目的是消除因設(shè)備運營環(huán)境差異或工作強度變化而帶來的失效強度變化.基于式(1),可構(gòu)建得到新的基于失效變點–算術(shù)失效強度減模型為

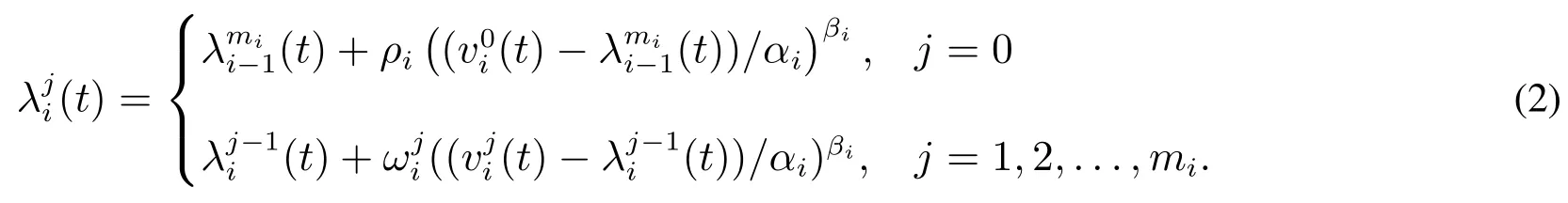
根據(jù)文獻[25],失效計數(shù)過程中,失效強度為單位時間內(nèi)的失效次數(shù).故設(shè)備失效強度和失效次數(shù)存在以下關(guān)系

根據(jù)式(2)和式(3),有

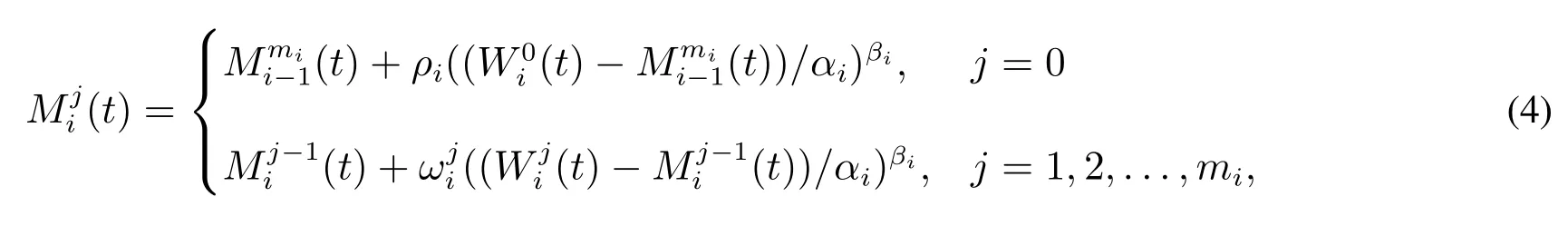
實際上,設(shè)備在運行過程中會受到預(yù)防維修的干擾,因此該值是一個理論值,可以根據(jù)初次失效強度建模得到.根據(jù)表1 和式(4),建模的具體步驟如下.

步驟1為數(shù)據(jù)轉(zhuǎn)換及預(yù)處理.如果采集的失效數(shù)據(jù)為失效時間間隔數(shù)據(jù),可以統(tǒng)計轉(zhuǎn)換為失效計數(shù)數(shù)據(jù),并整理得如表1 所示的數(shù)據(jù)類型.

步驟2建模數(shù)據(jù)集得到其概率分布進而應(yīng)用式(4)估計觀察時間點上的期望累積失效次數(shù)并確定固有失效強度.對于數(shù)據(jù)集可以采用較為常用的冪律模型或線性對數(shù)模型[3,25].同時,將能夠獲得的最早的預(yù)防維修區(qū)間內(nèi)的失效過程確定為固有失效強度.當(dāng)然,這樣確定的固有失效強度與設(shè)備真實的失效強度之間必定存在一定的差異,但維修質(zhì)量評估主要參考的就是維修前后的失效強度變化情況.因此,取能夠獲得的最早的失效過程為固有失效強度具有一定合理性.當(dāng)然,固有失效強度對維修質(zhì)量評估的影響值得在今后的研究中進一步探討.

步驟3估計ρi或.根據(jù)式(4),預(yù)防維修質(zhì)量可以通過最小化擬合值與觀察值之間的最小誤差平方和(sum of squares for error,SSE)得到.SSEij為

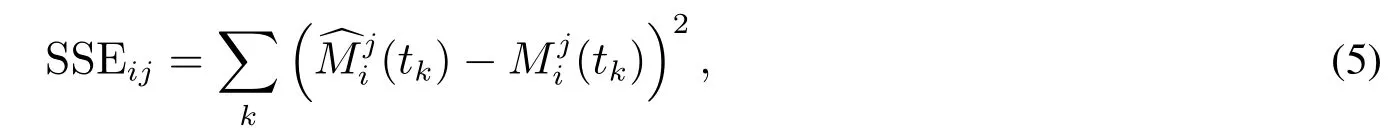
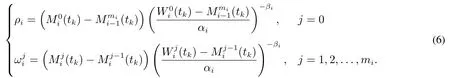
步驟4預(yù)防維修質(zhì)量評估.依據(jù)估計得到的ρi或值,根據(jù)模型構(gòu)建原理,可以推導(dǎo)當(dāng)ρi或取不同值時,系統(tǒng)失效強度經(jīng)歷一次預(yù)防維修后的變化情況.舉例來說,若ρi=1 或=1,系統(tǒng)經(jīng)歷第i個二級預(yù)防維修區(qū)間內(nèi)的第j次一級預(yù)防維修后的失效強度就等于(t).因為(t)是系統(tǒng)在第i個二級預(yù)防維修區(qū)間內(nèi)的第j ?1 次一級預(yù)防維修干預(yù)得到的系統(tǒng)在第i個二級預(yù)防維修區(qū)間內(nèi)的第j次一級預(yù)防維修區(qū)間內(nèi)的固有失效強度表現(xiàn).因此,ρi= 1 或= 1 意味著系統(tǒng)經(jīng)歷第i個二級預(yù)防維修區(qū)間內(nèi)的第j次一級預(yù)防維修后,其失效強度與該區(qū)間的系統(tǒng)固有失效強度表現(xiàn)一致.因此,與上一預(yù)防維修區(qū)間相比,相當(dāng)于修復(fù)如新.由此,可以推出不同ρi或值對應(yīng)的預(yù)防維修質(zhì)量如下:

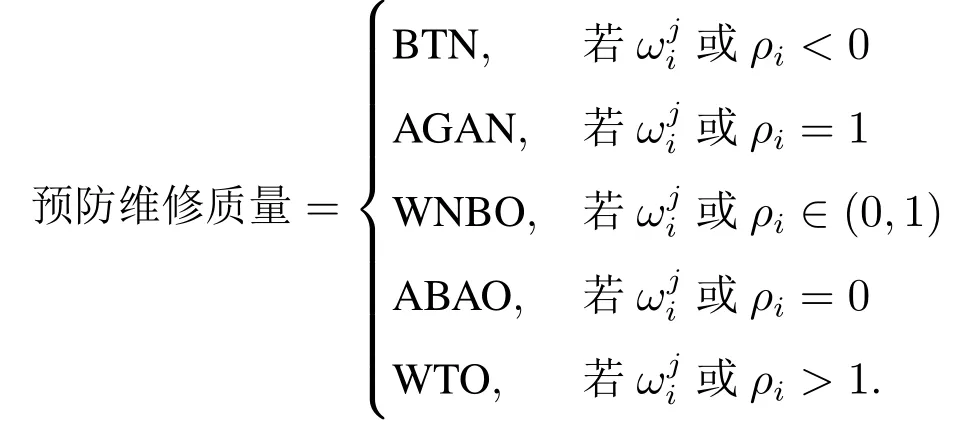
在本文建議的模型中,對于二級預(yù)防維修ρi是通過二級預(yù)防維修后至下一個一級預(yù)防維修來臨前的失效歷程來衡量的.現(xiàn)實中,二級預(yù)防維修的實際影響區(qū)間為一個完整的二級預(yù)防維修區(qū)間.換句話說,模型中的ρi是衡量整個二級預(yù)防維修區(qū)間內(nèi)的變化趨勢,而是衡量整個一級預(yù)防維修區(qū)間內(nèi)的變化趨勢.一旦能獲取充足的二級預(yù)防維修數(shù)據(jù)(至少在二級預(yù)防維修后再運行一個二級預(yù)防維修周期),可以對二級預(yù)防維修的維修效果ρi進行校對.

2.3 模型比較和驗證

為了說明模型的有效性, 本文建議的模型將與相似的三個模型進行對比, 這三個模型分別來自于文獻[18,20,23].文獻[23]給出的模型如式(1)所示.文獻[18]的模型可以描述為

其中φ是預(yù)防維修質(zhì)量.文獻[20]的模型是

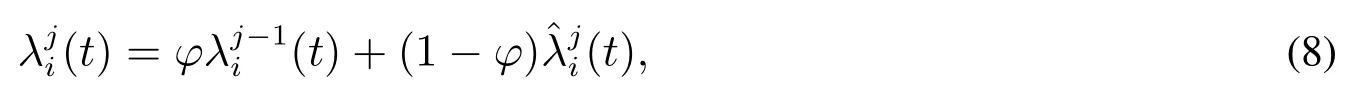
其中φ是預(yù)防維修質(zhì)量.

對比幾種模型,建議的模型參數(shù)的增加,勢必會導(dǎo)致具有更優(yōu)的擬合效果.為了避免此類情況的發(fā)生,可以通過構(gòu)建AIC 準(zhǔn)則或AICc 準(zhǔn)則進行擬合優(yōu)度比較.基于最小二乘法的AIC 準(zhǔn)則[26]為

本文的建模數(shù)據(jù)樣本較小,考慮基于最小二乘法的AICc 準(zhǔn)則[26]更為恰當(dāng).基于最小二乘法的AICc 準(zhǔn)則為

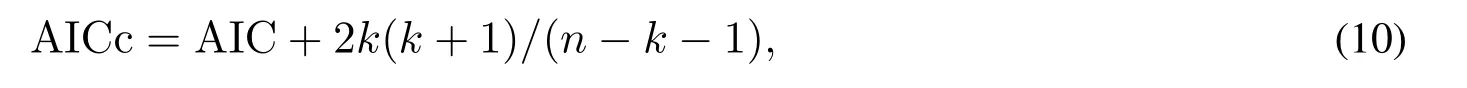
其中k為模型參數(shù)個數(shù),n為數(shù)據(jù)樣本量.一般來講,最小的AIC 值或AICc 值,具有最優(yōu)的擬合優(yōu)度.

為了進一步說明建議模型與其它模型的可比性,以及對存在的失效變點進行平滑的合理性,本文分析了原始數(shù)據(jù)的平均失效時間間隔(mean time between failures,MTBF),并以兩次預(yù)防維修區(qū)間內(nèi)的MTBF 改進量ΔMTBF 為依據(jù)開展驗證說明.這是因為MTBF是系統(tǒng)預(yù)防維修狀況的外在表現(xiàn).預(yù)防維修排除的潛在失效越多, 則系統(tǒng)的失效次數(shù)越少, 那么系統(tǒng)的MTBF 會越大.設(shè)第j個預(yù)防維修區(qū)間內(nèi)的MTBF為MTBFj,則

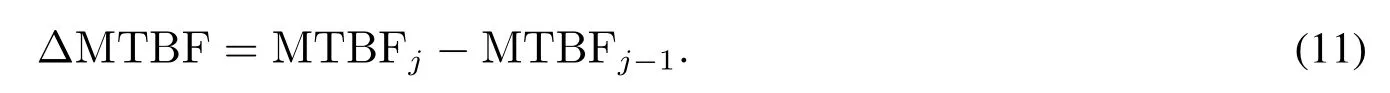
這樣,如果ΔMTBF>0,則意味著系統(tǒng)經(jīng)歷一次預(yù)防維修后運行狀態(tài)有改善,值越大改進程度越明顯;如果ΔMTBF=0,則意味著系統(tǒng)經(jīng)歷一次預(yù)防維修后運行狀態(tài)不變;如果ΔMTBF<0,則意味著系統(tǒng)經(jīng)歷一次預(yù)防維修后運行狀態(tài)保持比原來更差.由于ΔMTBF 和或(ρi)具有不同的變化范圍,可以將其進行0-1 標(biāo)準(zhǔn)化后進行比較.

3 數(shù)值例子

某巴士公司的管理信息系統(tǒng)詳細(xì)記錄了預(yù)防維修周期內(nèi)車輛發(fā)生的故障數(shù)據(jù)和所開展的維修活動.本文收集了該巴士公司一個車隊的預(yù)防維修數(shù)據(jù).在數(shù)據(jù)收集周期內(nèi),該公司對該車隊共進行了7 次二級預(yù)防維修.經(jīng)過整理得到了該車隊中巴士車輛在7 次二級預(yù)防維修周期內(nèi)的累積失效次數(shù),如表2 所示.表2中初始列表示車輛未進行二級預(yù)防維修前的初始失效過程,“1st”指車輛經(jīng)歷第1 次2 級預(yù)防維修后的失效過程,以此類推.不失一般性,對數(shù)據(jù)進行了脫敏處理,累積失效次數(shù)取的是車隊所有車輛的平均累積失效次數(shù).而這并不會影響到評估結(jié)果.此外,該車隊車輛在第5 次預(yù)防維修后的運營線路發(fā)生了變化,由于兩條線路的明顯差異,導(dǎo)致車輛失效趨勢發(fā)生明顯變化.因此,在第5 次預(yù)防維修效果評估時,可考慮應(yīng)用具有失效變點的評估模型進行處理.

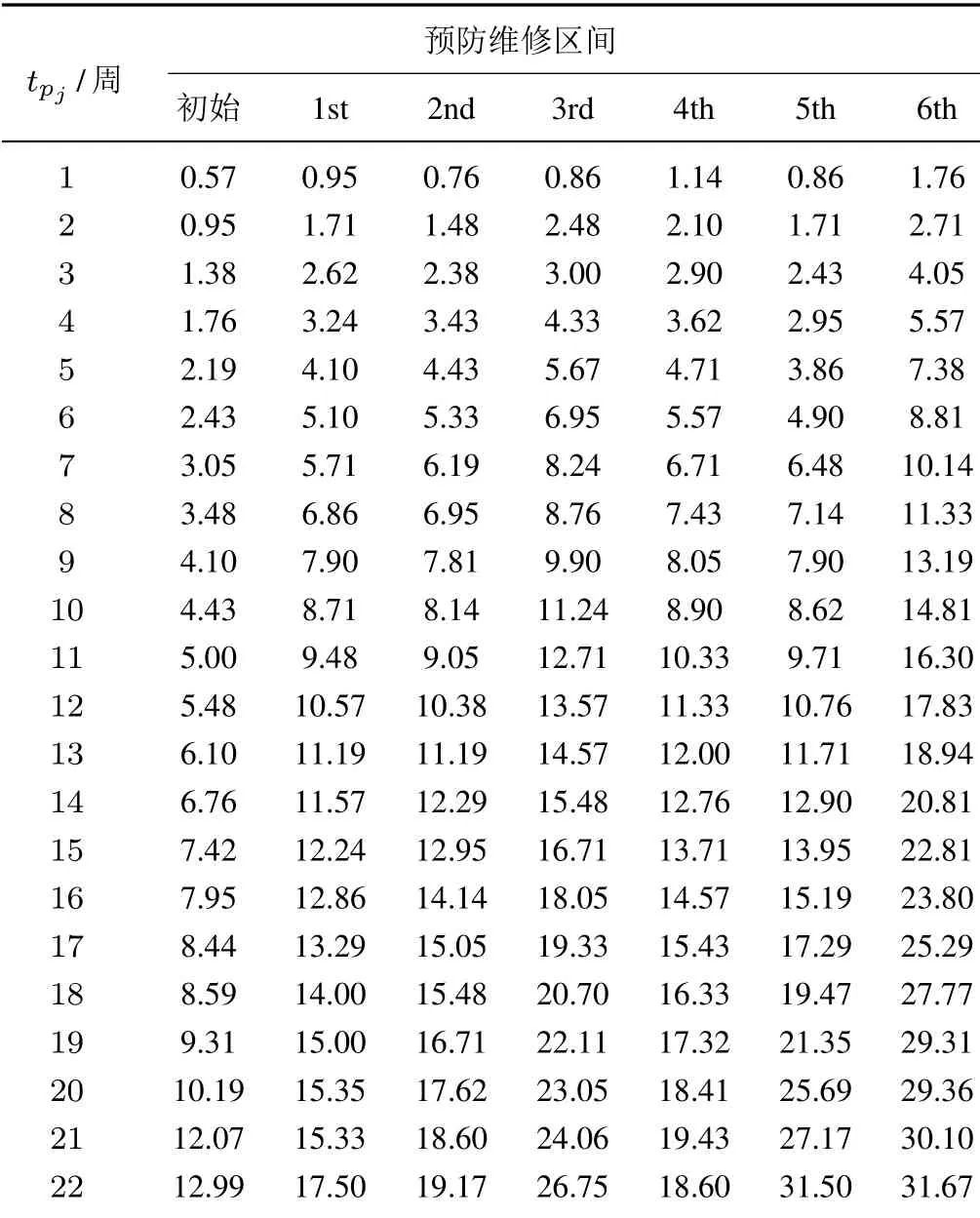
表2 巴士車輛的累積失效次數(shù)Table 2 Cumulative failure number of the urban bus

根據(jù)表2,應(yīng)用冪律模型對每一預(yù)防維修周期內(nèi)的失效次數(shù)進行模型,繼而應(yīng)用文獻[18,20,23]和本文的模型估計得到了前6 次預(yù)防維修的維修質(zhì)量.具體的建模步驟如下:

步驟1設(shè)將能夠得到的最早的失效記錄,即表2 中第一列數(shù)據(jù)確立為固有失效數(shù)據(jù).應(yīng)用三參冪律模型(tk)=((tk+θ)/φ)ψ建模(tk),參數(shù)估計得到θ=17.08,φ=17.14 和ψ=3.75.

步驟2應(yīng)用文獻[18,20,23]中的評估方法進行預(yù)防維修效果評估,得到的預(yù)防維修質(zhì)量如表3 所示,得到的SSEi也列在了表中.

步驟3觀察表3 中文獻[18,20,23]估計得到的SSEi會發(fā)現(xiàn),這三種方法得到的SSEi在第5 次預(yù)防維修時發(fā)生了突變.因此,可嘗試使用本文建議的模型建模第5 次和第6 次預(yù)防維修質(zhì)量.根據(jù)式(4),在文獻[23]評估的前4 次預(yù)防維修質(zhì)量基礎(chǔ)上,進一步估計得到了第5 次和第6 次的預(yù)防維修質(zhì)量,如表3 倒數(shù)第2 行和第3 行所示.在平滑建模時,參數(shù)估計得到α5=17.32 和β5=4.40.

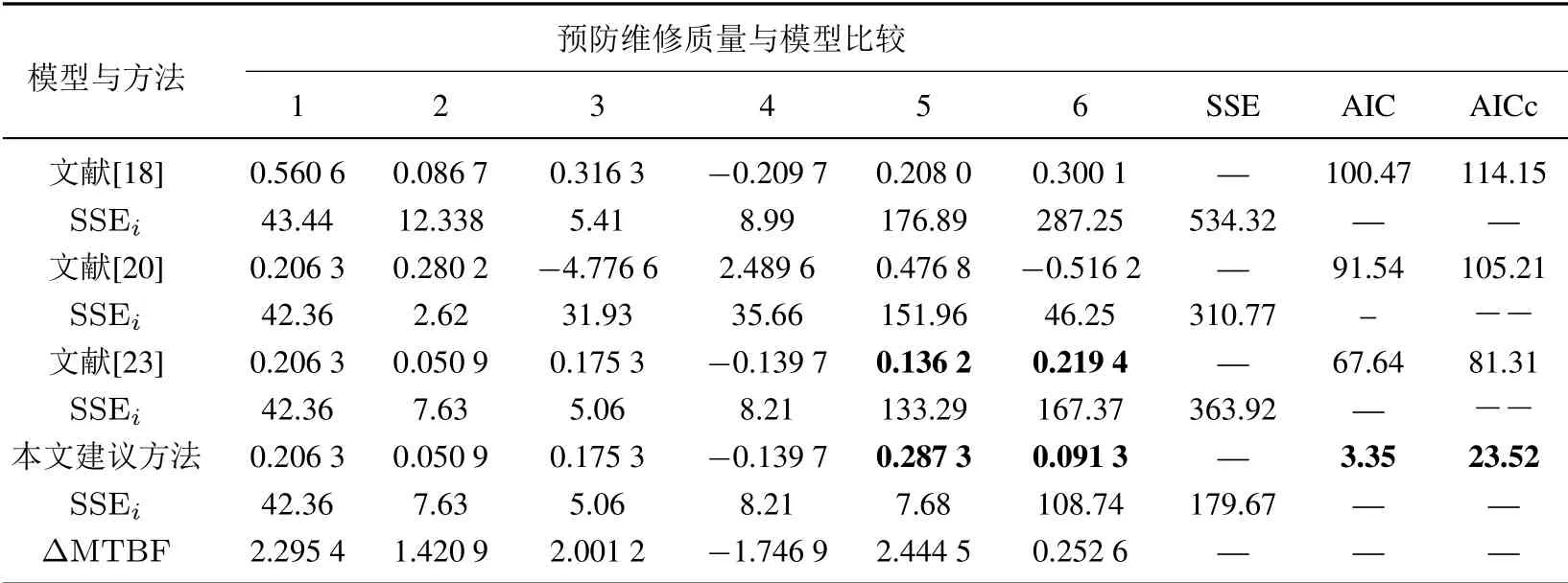
表3 建模結(jié)果Table 3 Modelling results

最終, 估計得到的預(yù)防維修質(zhì)量如表3 所示.根據(jù)表3 所示的建模結(jié)果, 本文建議的模型具有最小的SSE 值,AIC 值和AICc 值,故本文建議的模型具有最優(yōu)的擬合優(yōu)度.為了進一步說明參考模型與本文建議模型對預(yù)防維修質(zhì)量評估的有效性,根據(jù)2.3 節(jié)模型比較與驗證中所描述的驗證方法,通過原始數(shù)據(jù)計算得到了二級預(yù)防維修區(qū)間內(nèi)的ΔMTBF,如表3 最后一行所示.

根據(jù)表3 中的評估結(jié)果,運用0-1 標(biāo)準(zhǔn)化方法, 將文獻[18, 20, 23]和本文建議方法所得到的評估結(jié)果與ΔMTBF 進行對比, 比較結(jié)果如圖3 所示.可見本文建議方法得到的預(yù)防維修質(zhì)量變化曲線與實際的ΔMTBF 變化趨勢非常一致.為了說明一致性程度,進一步應(yīng)用歐式距離衡量了幾種方法與ΔMTBF 的相近程度.經(jīng)計算,文獻[18,20,23]和本文建議方法與ΔMTBF 的歐式距離分別為0.427 3,1.969 5,0.378 1和0.148 1.本文建議方法與ΔMTBF 具有最相近的趨勢變化,這進一步說明了本文方法的有效性.

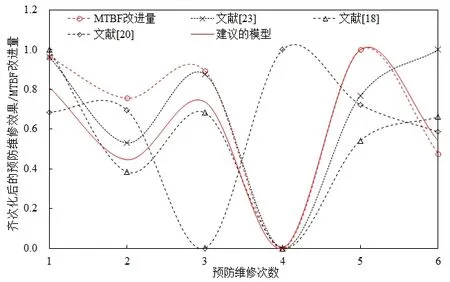
圖3 模型比較Fig.3 Comparison between models

4 結(jié)束語

在算術(shù)失效強度減模型中,通常假設(shè)設(shè)備的失效強度平滑變化.然而,發(fā)現(xiàn)現(xiàn)實情況中設(shè)備失效強度的變化有可能存在變點.因此,本文在前期研究工作基礎(chǔ)上,給出了一個具有失效變點的算術(shù)失效強度減模型.為了驗證方法的有效性,本文給出了以預(yù)防維修區(qū)間內(nèi)的MTBF 改進量的變化趨勢為衡量依據(jù),并以某巴士車輛的二級預(yù)防維修數(shù)據(jù)為例開展了案例研究.案例研究中,本文建議的建模方法與文獻已有相似的模型進行了比較.研究結(jié)果表明,本文建議的變點-算術(shù)失效強度減模型不僅具有更優(yōu)的模型擬合優(yōu)度,而且還具有與MTBF 改進量最小的歐氏距離,這表明本文建議的方法是有效可行的.