解兩類含參數(shù)的復(fù)合不等式有解與恒成立問題
江西省貴溪市第四中學(xué)(335400) 吳善祥
1 問題呈現(xiàn)
筆者在高三的一堂課上,講解了下面一道題.
題目關(guān)于x的不等式x2?2ax>4 ?a2在區(qū)間[0,1]內(nèi)恒成立,求實(shí)數(shù)a的取值范圍.
筆者提供的解法如下:
解(x?a)2?4 > 0,令f(x) = (x?a)2?4,由題意知f(x) > 0 在區(qū)間[0,1]內(nèi)恒成立,所以或即或解得a< ?2 或a> 3, 因此實(shí)數(shù)a的取值范圍為(?∞,?2)∪(3,+∞).
但課堂上有一個(gè)學(xué)生舉手示意他有另一種解法,想拿出來分享. 該學(xué)生的解法如下:
解x2?2ax> 4 ?a2?(x?a)2> 4?a
這位學(xué)生分享完他的解答之后,便向大家拋出了他那雙期待點(diǎn)贊的眼神.
筆者沒有著急給出評(píng)價(jià), 只是問該學(xué)生從“a
問題“a
2 問題探究
下面, 就來探討一下“a
“a
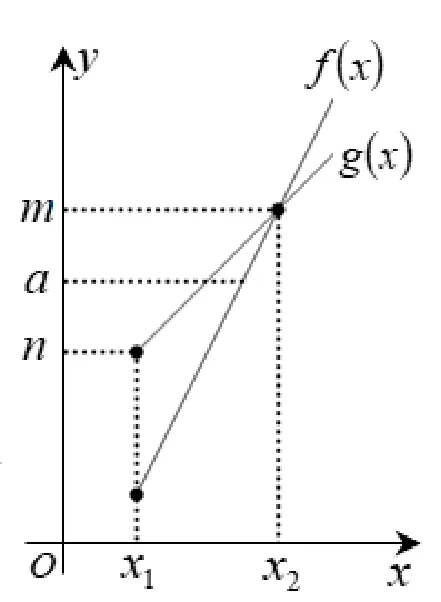
圖1
“g(x)≤a≤f(x)在區(qū)間D內(nèi)有解”又如何解決呢? 是否直接等價(jià)于“g(x)min≤a≤f(x)max”呢? 下面做進(jìn)一步的探究.
首先, 在區(qū)間D內(nèi)g(x)min和f(x)max都不一定存在,所以“g(x) ≤a≤f(x) 在區(qū)間D內(nèi)有解”直接等價(jià)于“g(x)min≤a≤f(x)max”是不嚴(yán)謹(jǐn)?shù)? 其次, 就算在區(qū)間D內(nèi)g(x)min和f(x)max存在,“g(x) ≤a≤f(x) 在區(qū)間D內(nèi)有解”也不一定等價(jià)于“g(x)min≤a≤f(x)max”.如圖2, 在區(qū)間[x1,x3] 內(nèi),f(x)max=m,g(x)min=n. 當(dāng)p 圖2 g(x) ≤a≤f(x) 在區(qū)間D內(nèi)有解, 務(wù)必確保f(x) ≥g(x),由f(x) ≥g(x)在區(qū)間D內(nèi)解出一個(gè)區(qū)間C,在區(qū)間C求g(x)的最小值g(x)min和f(x)的最大值f(x)max. 否則,x的取值區(qū)間有可能就被放大了,從而導(dǎo)致g(x)的最小值可能被縮小,f(x)的最大值可能被放大. 通過上面的研究,便得到解決“g(x) ≤a≤f(x)在區(qū)間D內(nèi)有解”這類題型的一般步驟如下: 第一步,控制區(qū)間: 在區(qū)間D內(nèi)解不等式f(x) ≥g(x),設(shè)其解集為C; 第二步,求出最值: 在區(qū)間C內(nèi),如果g(x)存在最小值,f(x)存在最大值,那么求g(x)的最小值g(x)min和f(x)的最大值f(x)max; 第三步,得出結(jié)論:g(x)min≤a≤f(x)max. 對(duì)于f(x)和g(x)在區(qū)間內(nèi)最值不存在的情況,一般可以考慮趨向于某個(gè)常數(shù)或者無窮大來處理此類問題. 后文碰到此類情況,類似處理,不再贅述. 現(xiàn)在回到前面的題目,便可以得到此題的另一種正確解法: 解法2x2?2ax>4?a2?(x?a)2>4?a 上面在由條件f(x) ≥g(x)控制的區(qū)間C內(nèi)去求g(x)的最小值和f(x)的最大值,其實(shí)都是在區(qū)間C是連續(xù)區(qū)間的情況下探討的. 如果區(qū)間C是多個(gè)連續(xù)小區(qū)間的并集,那么只要在每個(gè)小區(qū)間上分別去求參數(shù)a的取值范圍,最后將它們?nèi)〔⒓礊樗? 直到現(xiàn)在, 估計(jì)大家還有一個(gè)疑問, 既然“a 此時(shí),再來一題,看計(jì)算的結(jié)果是否一樣. 例1若a<6x?2 或a>x+2 在x∈[0,1]內(nèi)恒成立,則實(shí)數(shù)a的取值范圍是____. 錯(cuò)解因?yàn)閍< 6x?2 或a>x+ 2 在x∈[0,1]內(nèi)恒成立, 所以a< 6x?2 區(qū)間x∈[0,1] 內(nèi)恒成立或a>x+2 區(qū)間x∈[0,1]內(nèi)恒成立,所以a< (6x?2)min=?2 或a> (x+2)max= 3, 因此實(shí)數(shù)a的取值范圍為(?∞,?2)∪(3,+∞). 上面已經(jīng)探討了“a 類似于解決“g(x) ≤a≤f(x)在區(qū)間D內(nèi)有解”問題,很多學(xué)生容易得出“g(x) ≤a≤f(x)在區(qū)間D內(nèi)恒成立”的解題步驟: 第一步,控制區(qū)間: 在區(qū)間D內(nèi)解不等式f(x) ≥g(x),設(shè)其解集為C; 第二步,求出最值: 在區(qū)間C內(nèi),如果g(x)存在最大值,f(x)存在最小值,那么求g(x)的最大值g(x)max和f(x)的最小值f(x)min; 第三步,得出結(jié)論:g(x)max≤a≤f(x)min. 從正確與否的角度來看, 這種解題步驟是沒有問題的. 但從解題步驟的簡(jiǎn)潔性來說, 這種解題步驟還有待簡(jiǎn)化. “g(x) ≤a≤f(x) 在區(qū)間D內(nèi)恒成立”已經(jīng)確保了“f(x) ≥g(x) 在區(qū)間D內(nèi)恒成立”. 所以, 第一步在區(qū)間D內(nèi)不等式f(x) ≥g(x) 的解集C毫無疑問就等于D. 因此,在區(qū)間D內(nèi),若f(x)存在最小值,g(x)存在最大值, 則“g(x) ≤a≤f(x) 在區(qū)間D內(nèi)恒成立”直接等價(jià)于“g(x)max≤a≤f(x)min”,無需由f(x) ≥g(x)在區(qū)間D內(nèi)重新控制一個(gè)約束區(qū)間,給計(jì)算帶來沒有必要的麻煩. 例2若關(guān)于x的不等式|a?3x?1| ≤2x2在區(qū)間[1,2]內(nèi)恒成立,則實(shí)數(shù)a的取值范圍是____. 解|a?3x?1| ≤2x2??2x2+ 3x+ 1 ≤a≤2x2+ 3x+ 1. 在區(qū)間[1,2] 內(nèi),(?2x2+3x+1)max= 2,(2x2+3x+1)min=6. 因此a的取值范圍是[2,6].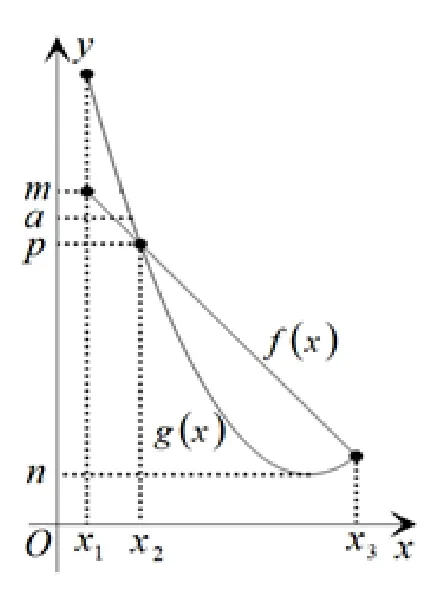


3 拓展延伸
3.1 g(x)≤a≤f(x)在區(qū)間D內(nèi)恒成立
3.2 a≤g(x)或a≥f(x)在區(qū)間D內(nèi)有解


