石雪飛, 王海燕

(東南大學經(jīng)濟管理學院,江蘇南京211189)

1 引 言

隨著經(jīng)濟和科技的發(fā)展,商品種類和數(shù)量越來越多.面對市場上種類繁多的產(chǎn)品,百貨商店,超市等零售商由于資金和庫存容量的限制,很難購進所有品牌和型號的產(chǎn)品,需要選擇收益高的產(chǎn)品銷售.在選擇產(chǎn)品時,有的產(chǎn)品銷量好,但體積大,利潤低.有的產(chǎn)品銷量不是很好,但利潤卻很高.在庫存容量限制下如何做出最優(yōu)的選擇?實際上,很多零售商選購產(chǎn)品時更多的是依靠主觀上的經(jīng)驗.

在學術領域,學者們更熱衷于研究供應商的選擇問題[1?3],僅有少量文獻研究產(chǎn)品的選擇問題[4],其中主要以普通產(chǎn)品和升級產(chǎn)品的選擇決策[5,6]為主.供應商選擇問題則是制造商或零售商們考慮產(chǎn)品質量,供貨能力,供應商信譽,采購成本和售后服務等因素,從而選擇出最有利的供應商.大部分供應商選擇的定量分析的文獻中,以最小化總成本為目標[7?9],而選擇產(chǎn)品時,零售商們通常優(yōu)先選擇收益高的產(chǎn)品.選對了供應商不意味著選對了產(chǎn)品.不同的產(chǎn)品售價和成本往往都不一樣,因此選擇成本小的產(chǎn)品可能不是最優(yōu)的選擇,故供應商選擇的研究并不適用于產(chǎn)品的選擇問題.

生產(chǎn)企業(yè)常用最小訂貨量來確定最優(yōu)的生產(chǎn)計劃[10,11],許多供應商要求采購企業(yè)的訂單至少要達到其最小訂貨量.但個性化的消費使得消費者對單一產(chǎn)品的依賴程度越來越低,導致了越來越多的小批量訂貨.規(guī)模小的零售商最優(yōu)訂貨量可能達不到供應商的最小訂貨量要求,按照最小訂貨量訂購產(chǎn)品會增加零售商的庫存成本.故本文將最小訂貨量作為產(chǎn)品選擇模型的一個約束條件.實際上,庫存容量限制和最小訂貨量限制是庫存補貨決策模型中很普遍的約束條件,如文獻[12–15]等.

最小訂貨量的限制以及小批量采購的高成本導致了越來越多的聯(lián)合采購.聯(lián)合采購通常是將小批量的訂單形成一個大訂單進行采購,這樣能夠形成規(guī)模經(jīng)濟效應,減小采購成本[16].顯然聯(lián)合采購能夠更容易滿足供應商的最小訂貨量的要求.然而,采購周期的協(xié)調(diào)是聯(lián)合采購的一個困難.單獨采購時一旦發(fā)現(xiàn)庫存水平低于訂貨點就可以立即采購.聯(lián)合采購時需要合作成員的需求量積累到一定的量或者等到約定的采購時間才會進行采購.采購之前有的成員庫存提前銷售完,在等待采購的過程中造成缺貨損失.若聯(lián)盟成員都愿意共享庫存那么就會降低缺貨損失.并且?guī)齑婀蚕砟軌蚪档蛶齑娉杀?減少運營成本,改善服務水平[17].因此本文考慮共享庫存的情況下進行聯(lián)合采購.

聯(lián)合采購問題的另外一個難點是分配問題,如何分攤費用或分配利潤是聯(lián)合采購聯(lián)盟達成的的關鍵.不公平的分配機制會導致聯(lián)盟成員退出合作聯(lián)盟[18].許多學者致力于研究聯(lián)合采購的成本/利潤分攤機制,Schotanus 等[19]調(diào)查發(fā)現(xiàn)87%的合作聯(lián)盟采用等價法分配收益,而13%的聯(lián)盟采用利于規(guī)模大的成員的分配方案.馮海榮等[20]研究了非瞬時補貨情況下易腐品聯(lián)合采購的分配問題,并給出了一個核分配方案.肖旦等[21]研究了產(chǎn)品中含有殘次品情況下的聯(lián)合采購模型.Heuvel 等[22]針對零售商多階段聯(lián)合補貨問題,建立了ELS(Eonomic lot sizing)博弈模型并證明了其核為非空的.可以看到這些文獻都應用合作博弈理論尋找核分配方案.這是因為核分配方案能夠促進聯(lián)合采購成員形成穩(wěn)定的合作聯(lián)盟,它能保證參與合作的成員收益最大化.但核分配方案并不總是存在的或容易找到的,不同合作環(huán)境下的核分配方案或接近核分配方案的近似核分配方案需要學者們?nèi)ヌ剿?

零售商選擇供應商時通常是選擇信用最好成本最低的供應商,而選擇產(chǎn)品時則會選擇利潤最高的產(chǎn)品.以前的文獻主要以供應商選擇為主,僅有少量文獻研究兩種產(chǎn)品的選擇,而目前并沒有文獻研究庫存容量和最小訂貨量約束下多產(chǎn)品的選擇和采購決策.故本文構建了庫存容量和最小訂貨量約束下的單獨采購時產(chǎn)品選擇和采購量決策模型.為進一步幫助零售商提高利潤,建立了庫存共享條件下的聯(lián)合采購模型.分別設計了多項式時間算法來求解這兩個模型.分配是合作的關鍵,因此,本文基于合作博弈利理論設計了利潤分配方案并證明了在聯(lián)盟庫存容量充足的情況下采用的分配方案是核分配方案而在庫存容量不足時采用的分配方案是滿足個人理性的并且能夠激勵零售商共享其真實的庫存容量信息的有效分配方案.數(shù)值實驗結果表明聯(lián)合采購能夠幫助合作聯(lián)盟提高26%的利潤.

2 單獨采購決策模型

假設:

1)零售商位于同一區(qū)域,不同零售商都以供應商建議的統(tǒng)一零售價銷售產(chǎn)品.

2)采購是瞬間完成的,沒有等待時間,即交貨期為0.

3)供應商已確定,采購成本參數(shù)已知.

本節(jié)研究零售商單獨采購時零售商決策是否選擇采購產(chǎn)品以及產(chǎn)品的采購量.各產(chǎn)品的采購是獨自完成的,采用的是連續(xù)采購策略,即當庫存不夠時立即補貨.下面是本文主要參數(shù)和假設: 某一區(qū)域有m個零售商,市場上有n個不同品牌的產(chǎn)品,由不同的供應商供應,記M={1,2,...,m},N={1,2,...,n}.供應商要求產(chǎn)品i,i ∈N需要達到的最小訂貨量記為產(chǎn)品i的體積為vi,產(chǎn)品i的固定采購費用為ki,采購價格為ci,零售價為pi.零售商j,j ∈M銷售產(chǎn)品i,i ∈N單位時間的需求到達率為λji,單位時間單位體積的庫存成本為h,零售商j的最大庫存容量為Vj.

零售商采用連續(xù)庫存檢查策略, 當產(chǎn)品i的庫存為0 時立即采購qji.產(chǎn)品i產(chǎn)生的總成本包括庫存成本和訂貨成本.零售商j的產(chǎn)品i的期望采購周期為qji/λji, 可得到其在一個周期內(nèi)總成本為若零售商以最大化長期平均期望利潤為目標,那么零售商j的優(yōu)化模型為

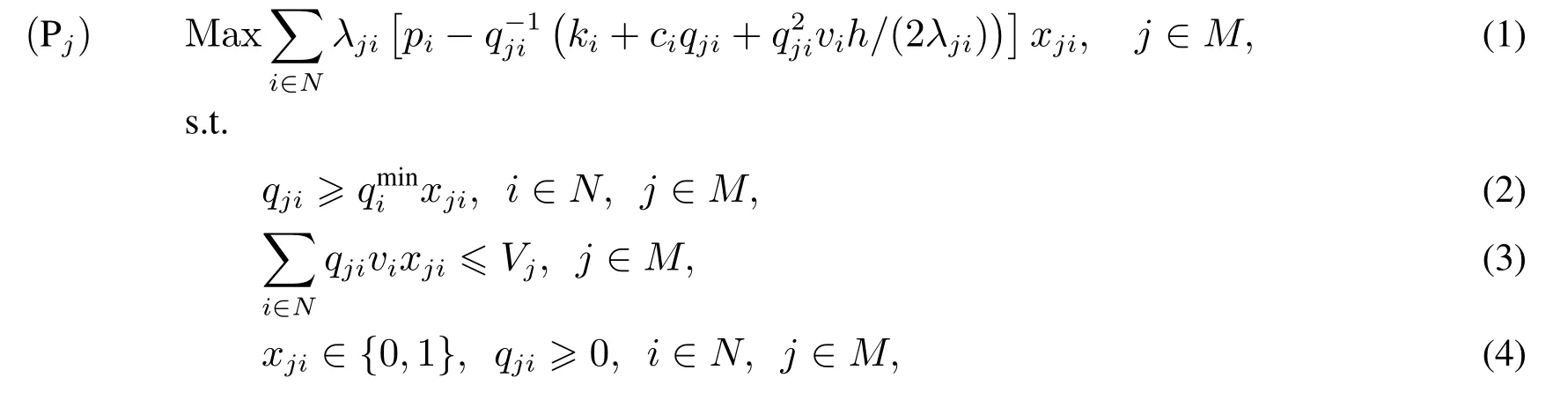
其中qji,xji為決策變量,qji是產(chǎn)品i的每個周期的采購量,xji=1 表示采購產(chǎn)品i,xji=0 則表示不采購采購產(chǎn)品i,式(2)為最小訂貨量約束,式(3)為庫存容量約束.

考慮模型(Pj)中的一個特殊情況,即

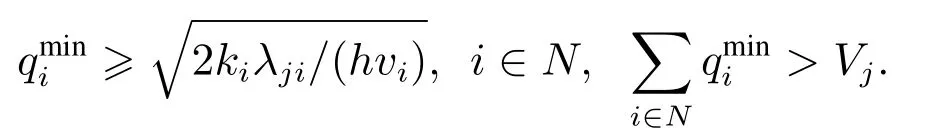
在此情況下只要產(chǎn)品i被采購,其最優(yōu)采購量為是一個確定值,只需決策xji.而此時通過模型(Pj)求解決策變量xji為一個經(jīng)典的二維背包問題,其中λjivi為物品體積,是為物品單位體積的價值,而Vj為背包的容量并且背包容量是不足的.

0-1 背包問題是NP–難的,目前仍然沒有證明存在多項式時間算法求得該問題的最優(yōu)解.模型(Pj)中的一個特殊情況時已經(jīng)是一個NP–難問題,為此,設計了多項式時間內(nèi)可解的啟發(fā)式算法來求解一般情境下的模型(Pj),證明在一定條件下可求得最優(yōu)解.

求解模型(Pj)的算法(記作算法1)步驟如下:

步驟1輸入?yún)?shù)值λji,pi,qmini ,ki,ci,h,vi,Vj,i ∈N;

步驟2

步驟3

步驟4找出{fl}l∈S中最大的值

步驟5如果fi′ >0 且

步驟6將S中i′刪除和更新剩余的庫存容量即

步驟7如果S=?或Vj=0 或fi≤0,i ∈S,那么終止算法;否則回到步驟2;

步驟8輸出結果

定理1算法1 是多項式時間算法,其時間復雜度為O(n2),并且當下列情況之一成立時算法1 得到的解為模型(Pj)的最優(yōu)解:

1)庫存容量充足.

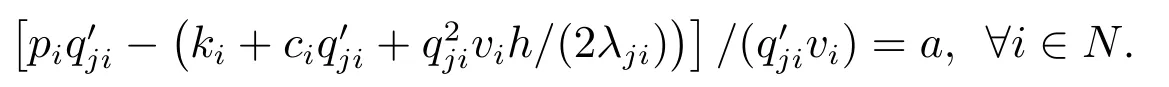
3)存在常數(shù)b,有λjivi=b,i ∈N.

證明首先證明算法1 是多項式時間算法.在算法1 中, 對于每個零售商, 找出第一個購進的產(chǎn)品需要計算n次qji和fi, 找出第二個購進的產(chǎn)品需要計算n ?1 次, 以此類推,總共要計算不多于n+(n ?1)+···+1 =n(n ?1)/2 次,而qji,fi的計算量是一個常數(shù),因此算法1 的計算時間復雜度為O(n2).

然后證明三種情況下,算法1 的解是模型(Pj)的最優(yōu)解.

情況1庫存容量充足.在此情況下式(3)的約束可以忽略掉,然后模型(Pj)可以分解成如下n個子模型

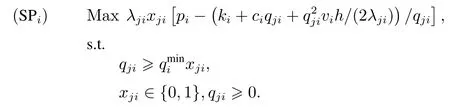
情況2存在常數(shù)a使得(piqji ?(ki+ciqji+(2λji)))(qjivi)?1=a,其中λji(pi ?(ki+ciqji+(2λji))是產(chǎn)品i的總利潤,[piqji ?(ki+ciqji+(2λji))](qjivi)?1是產(chǎn)品i單位體積的價值.

那么這個問題可以轉變成一維背包問題,λjivi是產(chǎn)品體積,Vj是背包容量,單位體積的產(chǎn)品價值是一樣的.一種產(chǎn)品可以看成一個物品,每個物品的單位體積的價值是一樣的,物品i的總價值為fi=λjivia,其中λjivi為物品的體積.那么背包里物品所占空間越大,背包里的價值越高.而算法1 是先選擇價值高的物品,也就是陸續(xù)將物品按體積從大到小裝進背包里,這樣背包裝的就是價值最高的.因此,算法1 得到的是最優(yōu)解.

情況3存在常數(shù)b,有λjivi=b,i ∈N.這種情況下同樣把這個問題轉化成一維背包問題,其中物品的體積為λjivi,物品的價值為fi.而物品的體積λjivi都是一樣的,對于固定的背包容量Vj,最優(yōu)的裝包方案是先裝價值高的物品.fi計算的正是產(chǎn)品i的總利潤即物品的價值,fi越大,物品的價值就越高,因此算法1 的解是最優(yōu)解. 證畢.

定理1 證明了算法1 是一個多項式時間算法,這也意味著當產(chǎn)品種類較多的時候,算法1 也能夠快速求解模型(Pj),但算法1 并不能保證得到的解是模型(Pj)的最優(yōu)解,只有滿足定理1 中三個條件的其中一個才是最優(yōu)解.

3 聯(lián)合采購決策模型

本節(jié)的目的是求出參與聯(lián)合采購聯(lián)盟所有成員的采購量和庫存目標.假設零售商愿意共享需求和庫存容量信息,存在一個可信賴的零售商或者第三方來組織聯(lián)合采購,組織者需要決策聯(lián)合采購的補貨量,并且聯(lián)合采購是在單獨采購決策之后的,即參與聯(lián)合采購的零售商的采購的產(chǎn)品種類是確定的,采購量則是需要聯(lián)合采購決策的.通過第2 節(jié)的模型(Pj),零售商們都確定了自己要采購的產(chǎn)品,不妨假設模型(Pj)的最優(yōu)解為若所有參與聯(lián)合采購聯(lián)盟的零售商共享采購周期,即聯(lián)合采購聯(lián)盟的零售商采購同一種產(chǎn)品的周期是一樣的.下面建立采購聯(lián)盟的長期平均利潤函數(shù)來確定聯(lián)合采購時產(chǎn)品的采購量.零售商j的產(chǎn)品i期望采購量記為為產(chǎn)品i的總采購量.由于采購周期一樣,所以也有記合作聯(lián)盟的產(chǎn)品i的總需求到達率為由于零售商們共享庫存,且交貨期為0.因此當所有零售商的產(chǎn)品i的庫存為0 時,聯(lián)盟向供應商發(fā)出一個聯(lián)合采購訂單量為Qi的訂單.那么產(chǎn)品i的期望采購周期為由集合M中成員形成聯(lián)盟的長期平均總利潤模型為

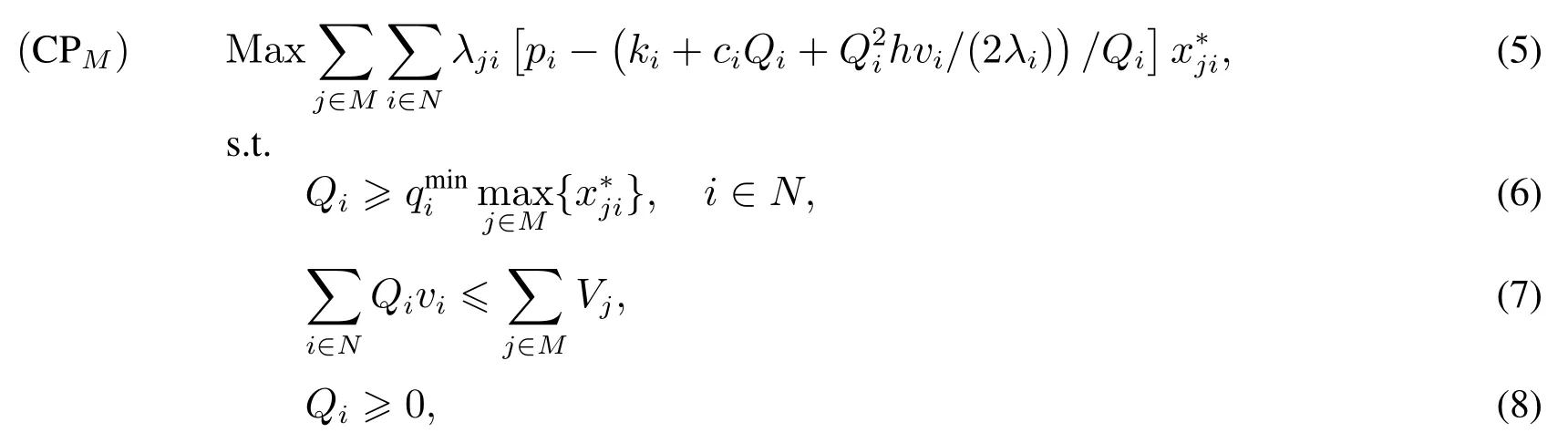
式(5)為最大化聯(lián)盟的單位時間內(nèi)的總利潤,決策變量為零售商的采購量Qi,式(6)為供應商最小訂貨量的約束,式(7)保證了零售商有足夠的庫存容量接收采購量,式(7)中的右邊是合作聯(lián)盟共享庫存后的總庫容量.

求解模型(CPM)的算法(記作算法2)步驟如下:

步驟1輸入?yún)?shù)λji,pi,,ki,ci,h,vi,Vj,,j ∈M,i ∈N;

步驟2計算下面的參數(shù)值,

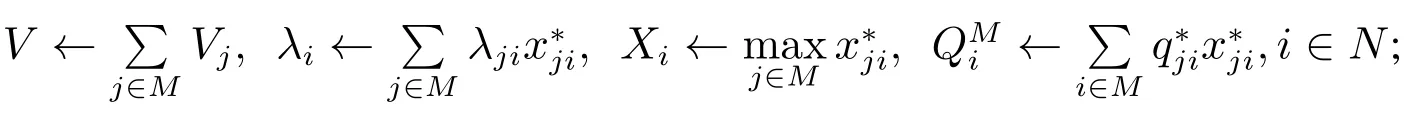
步驟3如果那么進入步驟8,否則進入步驟4;

步驟4?i ∈S,如果

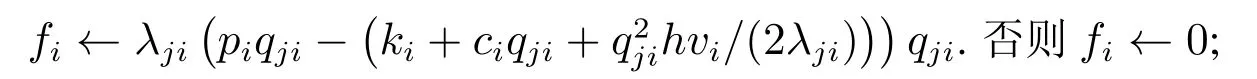
步驟5找出{fl}l∈S中最大的值記為fi′,如果fi′ >0,那么

步驟6將S中i′刪除和更新剩余的庫存容量即S ←S{i′},V ←V ?

步驟7如果S=?或V=0 或{fi≤0|i ∈S}進入步驟12,否則回到步驟4;

步驟8對于Xi= 1 且如果S′∪{i},否則更新聯(lián)盟庫存容量V,即V ←V ?若不滿足條件Xi=1 且=0,i ∈N,則進入步驟9;

步驟9

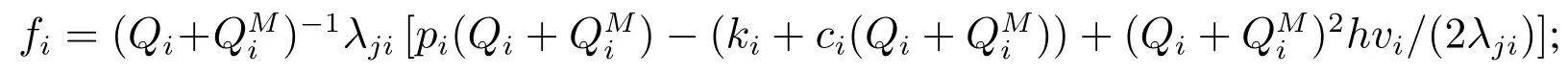
步驟10若fi′為{fl}l∈S′中最大的值,將S′中i′刪除和更新剩余的庫存容量即S′ ←S′{i′},V ←V ?Qi′vi′;

步驟11如果S′=?或V=0,則進入下一步,否則回到步驟9;

步驟12

步驟13如果Qji > Vj/vi, 那么否則Vj ←Vj ?Qjivi,i ∈M,j ∈N;

步驟14從{Vj}j∈M中找出最大的值找出中最大的值如果那么否則

步驟15若q′i=0,i ∈N,則結束算法2,否則回到步驟13;

步驟16輸出結果

當庫存容量不足時,首先保證每種產(chǎn)品的采購量不低于任何一個零售商單獨采購時的采購量,然后將庫存容量優(yōu)先分配給利潤高的產(chǎn)品.確定合作聯(lián)盟的總采購量之后,將聯(lián)盟的總采購量分配給聯(lián)盟成員,也就是從算法2 中的步驟11 開始,其計算量為O(nm)+O(nm)+O(n2).因此,算法2 也是多項式時間算法.注意到并不是零售商j每個周期對產(chǎn)品i的需求量,而是每個周期零售商j對產(chǎn)品i的目標庫存量.零售商j對產(chǎn)品i的需求量為但由于零售商j的庫存空間可能不夠,需要存儲在其他零售商的庫存容量里,從而可能導致

4 利潤分配方案設計

信息共享是合作聯(lián)盟合作的基礎,然而一個能讓聯(lián)盟所有成員接受的分配方案是合作的關鍵.公平合理的分配方案能夠促進采購聯(lián)盟長期穩(wěn)定的合作,而合作博弈理論是研究合作聯(lián)盟運作策略和穩(wěn)定性的理論,因此本節(jié)將基于合作博弈理論設計利潤分攤方案.

將由集合M中的成員參與合作的博弈定義為(M,ν),其中Π: 2M→R,ν(?) = 0.同時滿足下面條件的利潤分配方案為核分配方案或者稱這個分配方案是在聯(lián)合采購博弈的核中的,即

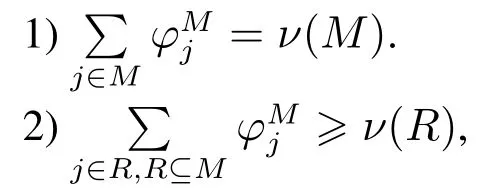
其中是合作聯(lián)盟M分配給成員j的利潤.

滿足1)的分配方案稱為有效分配方案.把所有成員都參與合作形成的合作聯(lián)盟稱為大聯(lián)盟.R為M的子集,子聯(lián)盟R所產(chǎn)生的利潤是不大于R中所有零售商從大聯(lián)盟的所獲的利潤之和的.故從利潤的角度上考慮,子聯(lián)盟R若是理性的集體則不會脫離大聯(lián)盟來形成小聯(lián)盟R的,因為子聯(lián)盟R無法得到更高的利潤.同時可以看到R={j}時,≥ν({j}),這意味著合作之后零售商分配到的利潤不會比單獨采購所產(chǎn)生的利潤低.故從利潤的角度上考慮,對于理性的零售商而言是不會采取單獨采購的.1)和2)表明核分配方案是滿足集體理性和個體理性的有效分配方案,它能保證任何子聯(lián)盟離開大聯(lián)盟都不能獲得更大收益.因此,核分配方案能夠保證理性的零售商都參與合作,因為他們都參與合作能夠獲得最大的利潤.

定義聯(lián)合采購博弈(M,Π),其中Π是聯(lián)合采購聯(lián)盟的總利潤,那么合作聯(lián)盟M的總利潤為

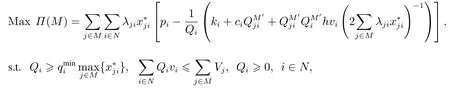
其中剔除了不采購的產(chǎn)品.那么易知Π(M)的最優(yōu)解和模型CPM的最優(yōu)解是相同的,Π({j})的最優(yōu)解和模型(Pj)的最優(yōu)解是相同的.

引理1聯(lián)合采購博弈是超可加的.

證明設R,T ?M且R ∩T=?,R ∪T=H,分別是Π(R),Π(T),Π(H)的最優(yōu)解.記是Π(H)的一個可行解,所以有

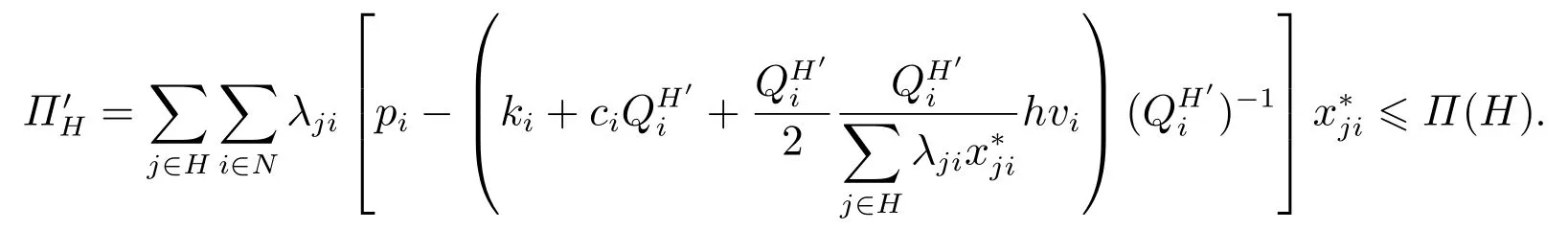
又因為Π′H≥Π(R)+Π(T),所以有Π(R)+Π(T)≤Π(H). 證畢.

超可加博弈是核分配方案存在的必要條件,引理1 表明這個合作博弈的核是有可能找到的.

下面首先給出兩種分配方案,記

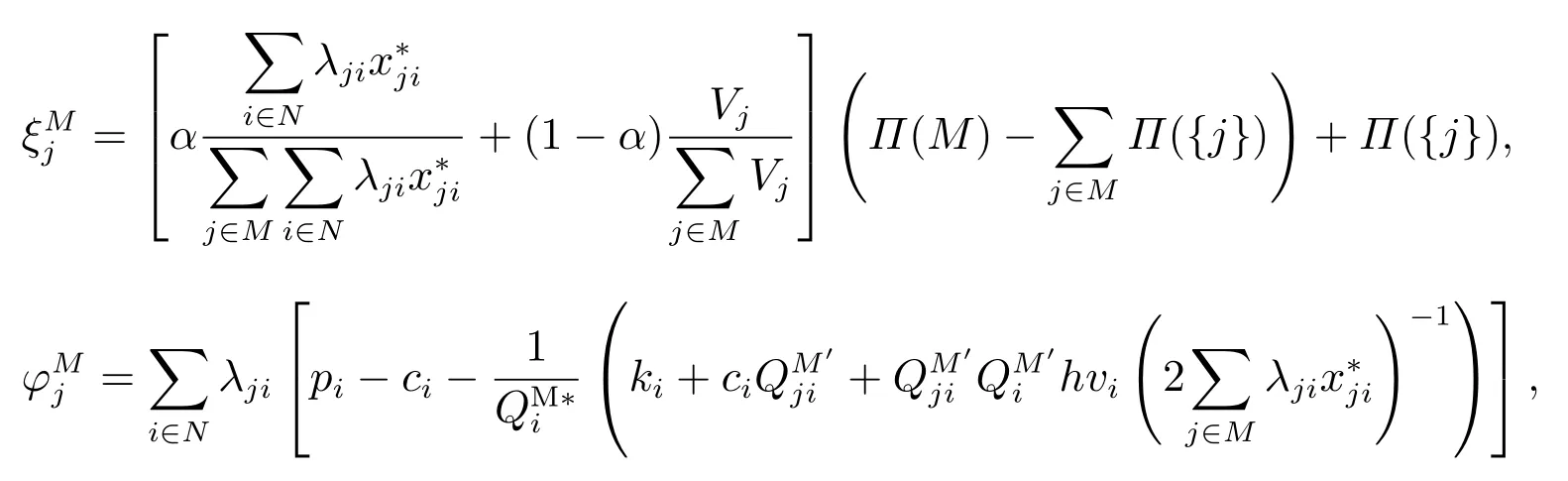
其中分別表示聯(lián)合采購聯(lián)盟M分配給零售商j的利潤分配方案,是Π(M)優(yōu)化模型的最優(yōu)解.

定理2當分配方案φ= (φ1,φ2,...,φm)是聯(lián)合采購博弈的核分配方案.當分配方案ξ=(ξ1,ξ2,...,ξm)是滿足個人理性的有效方案.

證明1)即聯(lián)合采購聯(lián)盟的庫存容量充足.首先,

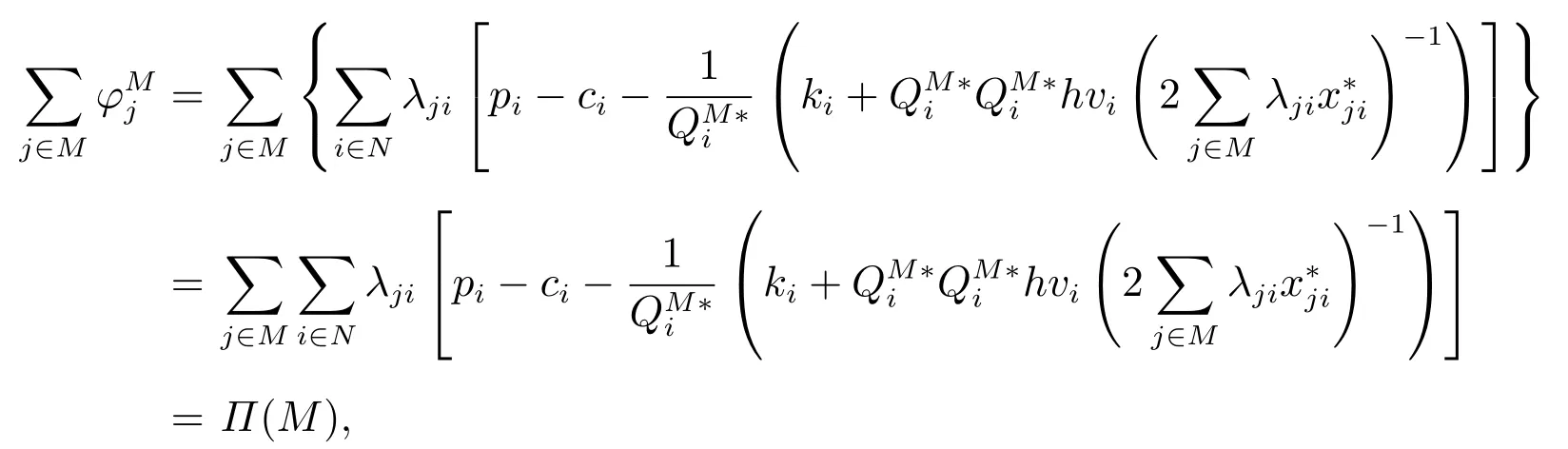
因此,φ=(φ1,φ2,...,φm)是一個有效分配方案.記為Π(R)的最優(yōu)解,聯(lián)合采購聯(lián)盟的庫存容量是充足的,產(chǎn)品i的最優(yōu)訂貨量為那么

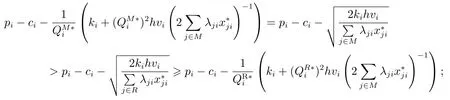
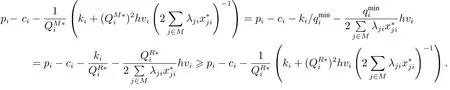
故

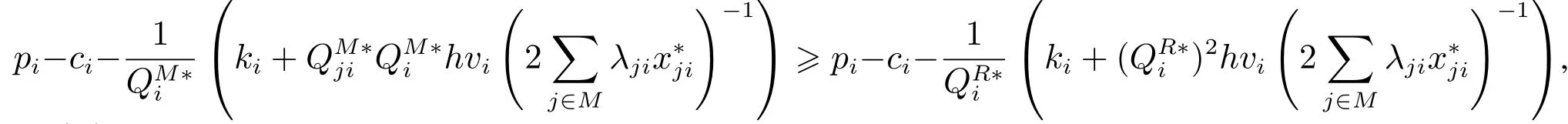
因此有

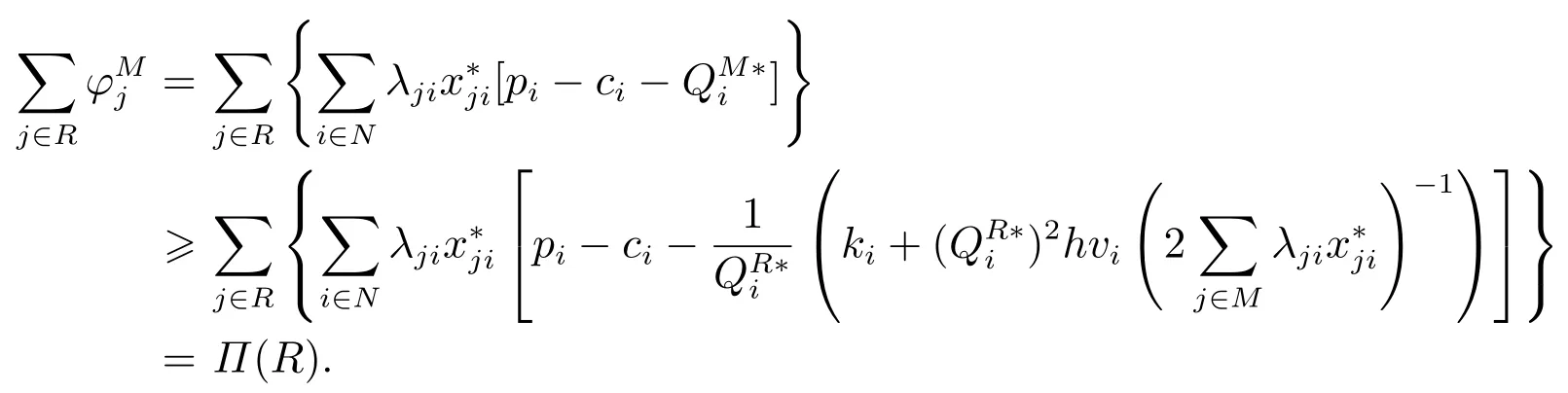
因此,分配方案φ=(φ1,φ2,...,φm)是聯(lián)合采購博弈的核分配方案.

首先有

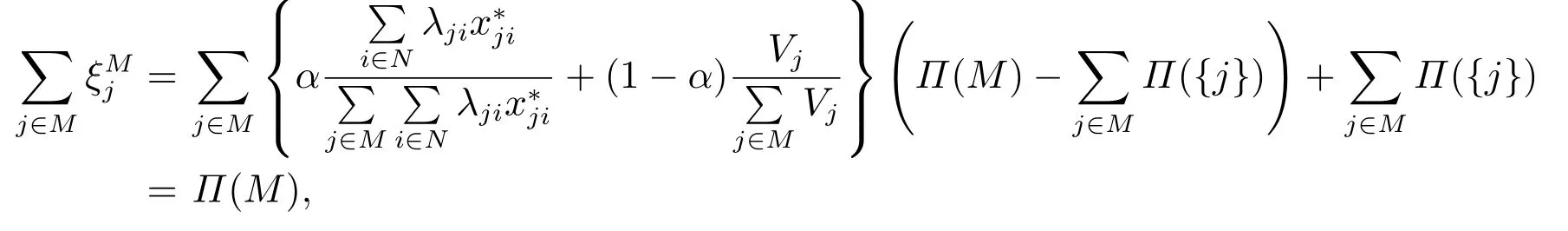
因此,分配方案ξ=(ξ1,ξ2,...,ξm)是有效分配方案方案.

情況I

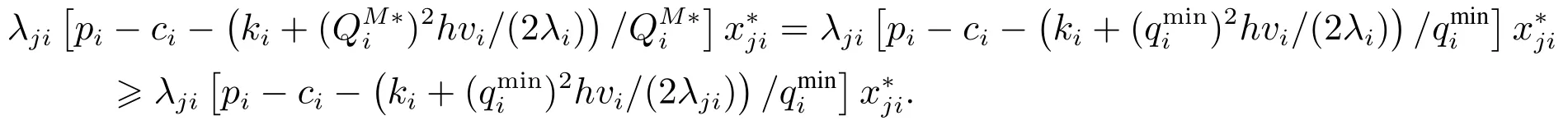
情況II

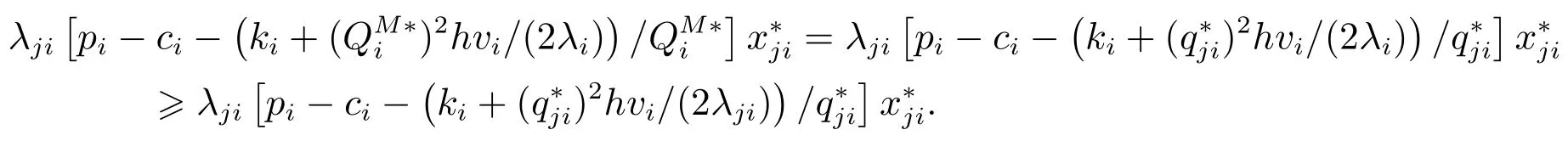
綜合情況I 和情況II,可知

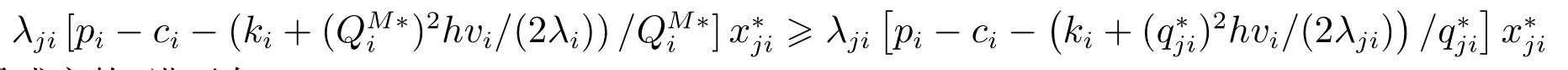
總是成立的.進而有

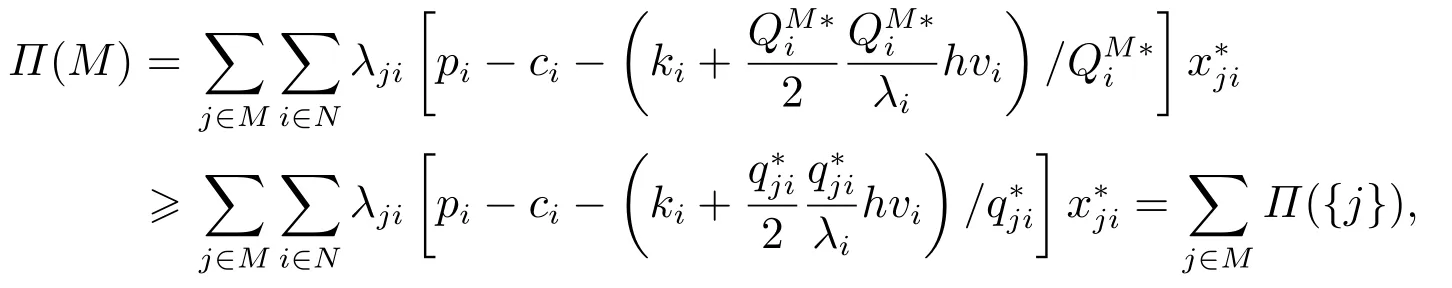
這保證了合作之后分配到的利潤不會比單獨采購時獲得的利潤低,說明分配方案ξ= (ξ1,ξ2,...,ξm)是滿足個體理性的.因此,分配方案ξ=(ξ1,ξ2,...,ξm)是滿足個體理性的有效分配方案. 證畢.

定理中的φj,ξj是庫存容量充足和不足的情況下在單位時間內(nèi)分別獲得的收益.這個收益可以表示為銷售收入減掉采購成本和存儲成本,而銷售入和存儲成本通常是零售商自己管理的,聯(lián)合采購聯(lián)盟只管理采購費用.因此需要計算每次采購的零售商應該支付的采購費用.并且不同產(chǎn)品的采購周期可能不一樣,因此,下面計算零售商j在采購產(chǎn)品i時所需支付的費用.值得注意的是若計算結果為證表示零售商向聯(lián)盟支付的費用,若為負則表示聯(lián)盟向零售商支付的費用.

φj是聯(lián)盟庫存容量充足的情況下零售商j最終分配到的利潤,合作聯(lián)盟可以通過零售商支付采購成本來達到利潤的分配.假設銷售的收入歸零售商自己所有,庫存產(chǎn)生的成本也由零售商自己承擔,每次采購聯(lián)盟收取相應的采購成本.由于庫存共享,零售商j的庫存量未必是零售商j的需求量.定理2 的分配方式實際上是按照需求比例分攤固定成本,各自承擔自己所需采購量的采購成本和存儲成本.且算法2 得到的是零售商j產(chǎn)品i的庫存量,那么聯(lián)合補貨時零售商j產(chǎn)品i的每次采購應該承擔的采購成本為

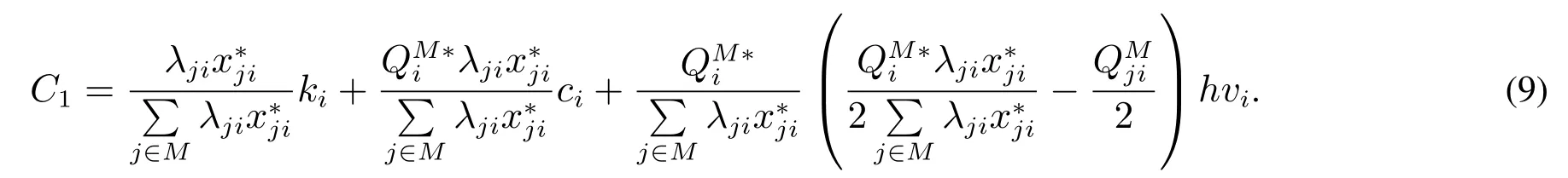
式(9)右邊的第2 項是零售商j每個周期產(chǎn)品i的需求量,而是存儲在零售商j的產(chǎn)品i庫存量.若是零售商j庫存空間里的存儲量比需求量大,那么說明零售商j的部分庫存空間被其他零售商所用,被占用的庫存產(chǎn)生的庫存成本需要其他零售商對零售商j進行補償,式(9)右邊的第3 項即是零售商j獲得補償庫存成本的費用.若是需求量比庫存量大,那么零售商j獲得的該項費用表示零售商j對其他零售商的庫存成本的補償,這樣就能保證零售商j承擔了自己產(chǎn)品產(chǎn)生的存儲成本,從而達到零售商單位時間產(chǎn)生利潤φj的目標.

ξj是聯(lián)盟庫存容量不足的情況下零售商j最終分配到的利潤,合作聯(lián)盟同樣通過零售商支付采購成本來達到利潤的分配.因此,下面計算零售商j每次采購產(chǎn)品應該支付的采購成本.

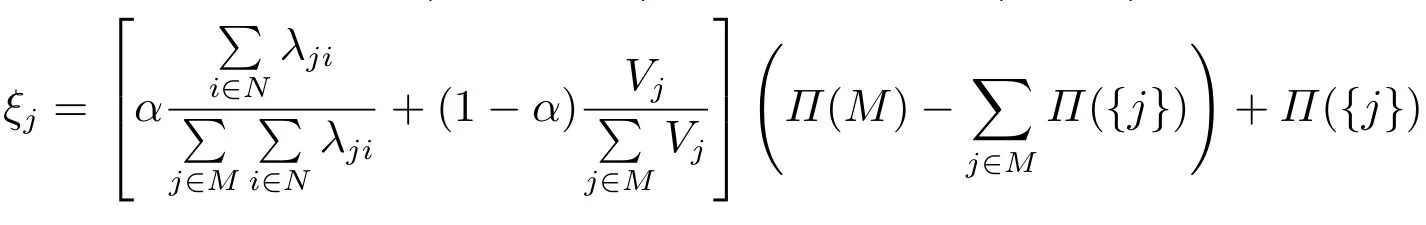
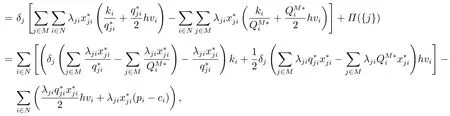
那么零售商j產(chǎn)品i單位時間內(nèi)需要承擔的成本為

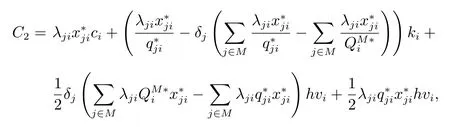
而一個周期需要承擔的成本為

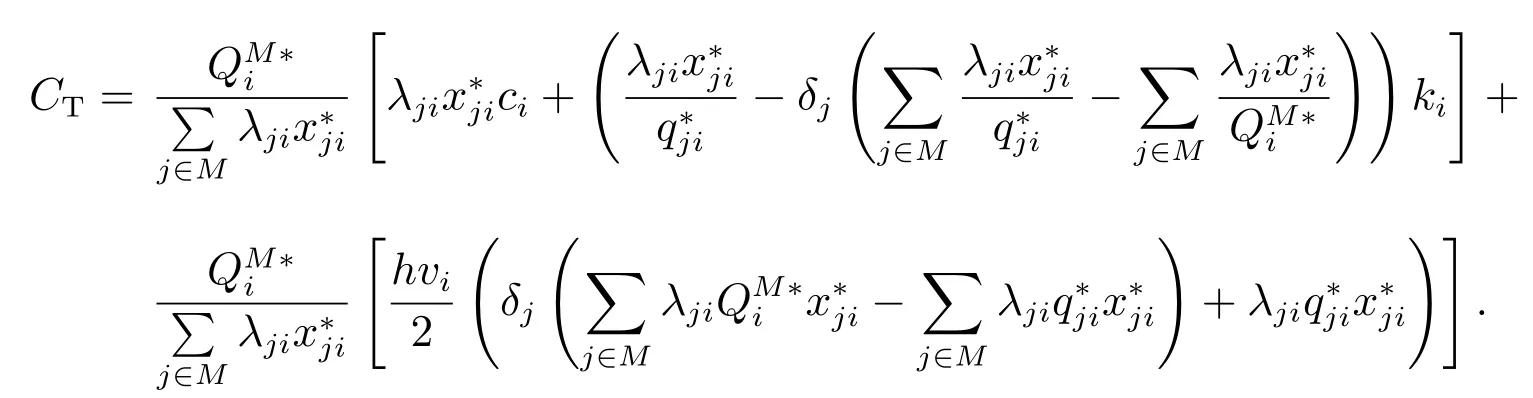
CT是采購成本和存儲成本之和.而這個周期內(nèi)零售商j自己庫存會產(chǎn)生存儲成本所以聯(lián)盟每次采購產(chǎn)品i時零售商j應該承擔的采購成本為

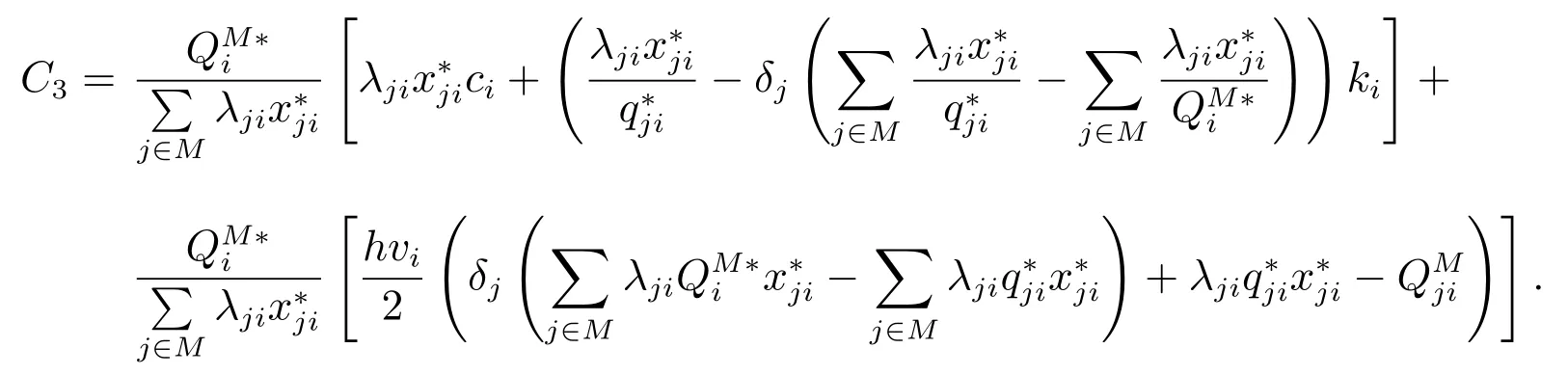
通過定理2 的證明可知, 這個收益能保證合作后的利潤全部分配完, 每個零售商的利潤都能夠增大, 并且當聯(lián)盟的庫存容量充足時任何子聯(lián)盟收益都不會比參與大聯(lián)盟合作的收益更大.因此, 對于理性的零售商來說, 這樣的核分配方案能夠促使他們形成穩(wěn)定的合作.盡管定理2 中的核分配方案是需要聯(lián)盟庫存容量充足的條件, 但這個給定條件并不會太苛刻.當參與聯(lián)合補貨的零售商越多,條件越容易達到,這是因為根據(jù)算法1 的計算過程,在單獨決策時零售商最多只有一種產(chǎn)品的訂貨量不是而聯(lián)合采購通常能夠減小零售商的訂貨量,從而節(jié)省庫存容量使得最后一種產(chǎn)品也經(jīng)常能達到最優(yōu)訂貨量.下面用一個簡單例子來說明合作之后減少了庫存水平.

例1若三個零售商決策購進五種產(chǎn)品, 這五種產(chǎn)品的最小訂貨量分別取qmin= 60,50,60,30,20, 產(chǎn)品售價p= 10,25,25,25,25, 單位產(chǎn)品的采購費用c= 2.500 0,6.250 0,6.250 0,6.250 0,6.250 0, 產(chǎn)品體積v= 0.100 0,0.250 0,0.050 0,0.500 0,0.350 0, 固定采購費k= 100,50,10,50,90, 各零售商庫存容量V=30,60,45,單位體積單位時間的庫存成本h=1,各零售商的需求到達率為

當零售商單獨決策時,通過算法1 可得到他們的采購量為

當三個零售商庫存容量都增加到75 時,他們單獨決策式的采購量為

這說明當庫存容量充足時所有產(chǎn)品都是能夠盈利的, 而庫存容量為30,60,45 時, 零售商的庫存容量是不夠的, 因為他們都選擇放棄采購至少一種產(chǎn)品.而當他們聯(lián)合采購時, 各產(chǎn)品的總采購量為Q= 94.701 5,64.477 9,60.000 0,76.124 6,130.193 7, 占用庫存容量為112.219 7, 比他們的總庫存容量135 小.聯(lián)合采購是在零售商確定了采購產(chǎn)品之后發(fā)生的,當零售商們選擇的產(chǎn)品都高度一致時,聯(lián)盟庫存容量總是會有剩余的,說明總庫存水平降低了.但當零售商選擇了很多不一樣的產(chǎn)品導致能形成聯(lián)合采購的產(chǎn)品比較少,這樣聯(lián)盟庫存容量不夠的概率會增加,如下面的例2.

例2若兩個零售商決策購進三種產(chǎn)品, 這三種產(chǎn)品的最小訂貨量都為0, 即qmin= 0,0,0, 產(chǎn)品售價p=60,120,140,單位產(chǎn)品的采購費用c=10,15,20,產(chǎn)品體積v=1,1,1,固定采購費k=50,50,50,各零售商庫存容量V=80,80,單位體積單位時間的庫存成本h=1,各零售商的需求到達率為當零售商單獨決策時,通過算法1 可得到他們的采購量為當零售商聯(lián)合采購量時,三種產(chǎn)品的聯(lián)合采購量分別為3,57,100,聯(lián)盟的庫存容量是不足的,只有產(chǎn)品3 形成了聯(lián)合采購.若需求到達率為16,13,0 的零售商3 加入聯(lián)合采購聯(lián)盟,并且零售商3 的庫存容量為70.單獨采購時,零售商的采購量為34,36,0,沒有達到其最優(yōu)采購量40,36,0.但當三個零售商一起聯(lián)合采購時,合作聯(lián)盟的采購量為60,70,100,正好達到無庫存容量限制下各產(chǎn)品的最優(yōu)采購量,這個聯(lián)盟的庫存容量是充足的.這時候產(chǎn)品1,產(chǎn)品2 和產(chǎn)品3 都形成了聯(lián)合采購,節(jié)省了更多的庫存容量空間.

定理2 給出的分配方案在聯(lián)盟庫存容量不足的情況下只是滿足個人理性的有效分配方案,無法保證聯(lián)盟的穩(wěn)定.并且是很難找到核分配方案的,這是因為通過第2 節(jié)對模型(Pj)的分析容易知道在庫存容量不足時,目前也無法確定能找到多項式時間內(nèi)的算法能夠求解CP(M)的最優(yōu)解.而近似解是有可能導致子聯(lián)盟R(R ?M)比大聯(lián)盟M得到更優(yōu)的解從而發(fā)生子聯(lián)盟R的總利潤比大聯(lián)盟M的利潤更大,這種情況下找核分配方案是不現(xiàn)實的.

定理2 中給出的分配方案φ= (φ1,φ2,...,φm)實際上也是聯(lián)合采購聯(lián)盟庫存容量不足情況下滿足個人理性的有效分配方案.但使用分配方案ξ= (ξ1,ξ2,...,ξm)是因為這個分配方案能夠激勵參與聯(lián)合采購的零售商共享庫存容量(α<1).ξj的表達式中很容易看到零售商j的庫存容量占聯(lián)盟的庫存容量比例越大收益就會越多.在庫存容量不足的情況下,庫存容量是聯(lián)合采購的稀缺資源,增大庫存容量會增加聯(lián)合采購聯(lián)盟的利潤.因此有必要通過利潤來激勵零售商共享其真實的庫存容量.而在庫存容量充足時,庫存容量不再是稀缺資源,無法通過增加庫存容量來提高聯(lián)盟的利潤,若是通過利潤激勵零售商會導致零售商虛報庫存容量而造成分配的不公平.

5 數(shù)值實驗

5.1 零售商單獨決策的算例分析

本節(jié)通過數(shù)值算例調(diào)查庫存容量和最小訂貨量對零售商利潤的影響.下面給出一個10 種產(chǎn)品的例子,其中h=1,V=75,其它參數(shù)如表1.本節(jié)沒有特別說明都使用表1 中的參數(shù)值以及h=1,V=75.

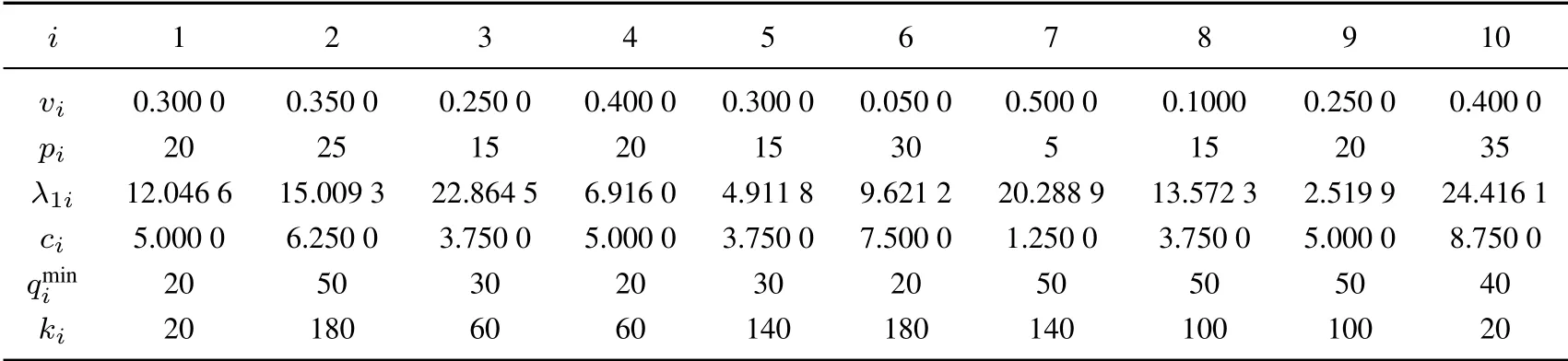
表1 模型(Pj)的參數(shù)值Table 1 Parameter values of the model(Pj)

首先研究供應商的最小訂貨量對零售商的影響.將產(chǎn)品1 的最小訂貨量從4 增大到200,得到零售商1的總利潤曲線圖,如圖1.可以觀察到零售商的總利潤變化在區(qū)間[20,72]內(nèi).為進一步分析這個變化過程,將零售商在供應商最小訂貨量區(qū)間[20,72]內(nèi)的最優(yōu)訂貨量計算出來,得到表2.表2 中第2 列至第11 列分別是產(chǎn)品1 至產(chǎn)品10 在產(chǎn)品1 最小訂貨量變化時的訂貨量.從表2 中可以看到產(chǎn)品1 的最小訂貨量為20 時,零售商產(chǎn)品1 的訂貨量為21.951 4,說明零售商最優(yōu)訂貨量是大于供應商最小訂貨量的,供應商最小訂貨量小小于21.951 4 時不會影響零售商的決策,因此利潤也不會變化.而當供應商最小訂貨量大于21.951 4 時,零售商的產(chǎn)品1 的訂貨量就是供應商要求的最小訂貨量,并且隨著最小訂貨量增大而影響其它產(chǎn)品的決策,這也就造成了圖1 中零售商總利潤突然大幅度下降.當供應商要求的最小訂貨量大于64 時,產(chǎn)品1 被放棄采購,并且總利潤反而提高了.說明之前的解并不是最優(yōu)解,這是因為這種情況并沒有滿足定理1 的條件.

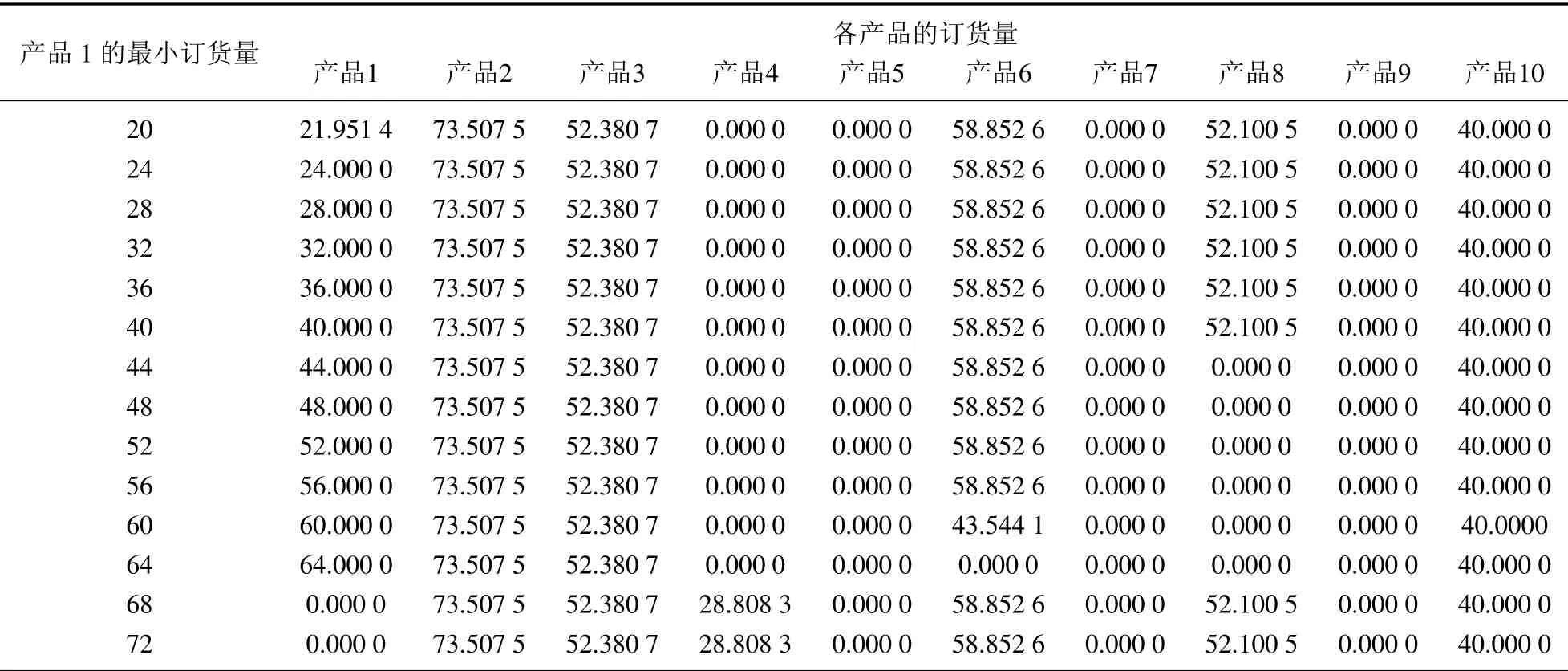
表2 產(chǎn)品訂貨量Table 2 The order quantity of product

接下來研究產(chǎn)品需求到達率對零售商利潤的影響.將產(chǎn)品1 的需求到達率從0 開始增大到500,其它參數(shù)仍然用表1 的數(shù)值,另外給出了一個庫存容量為150 但其它都一樣的零售商的利潤曲線作為對比,得到了圖2.圖2 中V= 75 的這條曲線整體呈上升趨勢,但有的點突然下降,這是因為有的產(chǎn)品訂貨量逐漸減當減小到低于最小訂貨量時就會被放棄采購,而零售商總利潤突然下降的點就是被放棄采購的臨界點.但V= 150 時,庫存容量總是充足的,產(chǎn)品1 的訂貨量上升,但沒有影響的其它產(chǎn)品的決策.其它產(chǎn)品需求到達率不變的情況下,零售商的總利潤隨產(chǎn)品1 的需求到達率增大而增加.

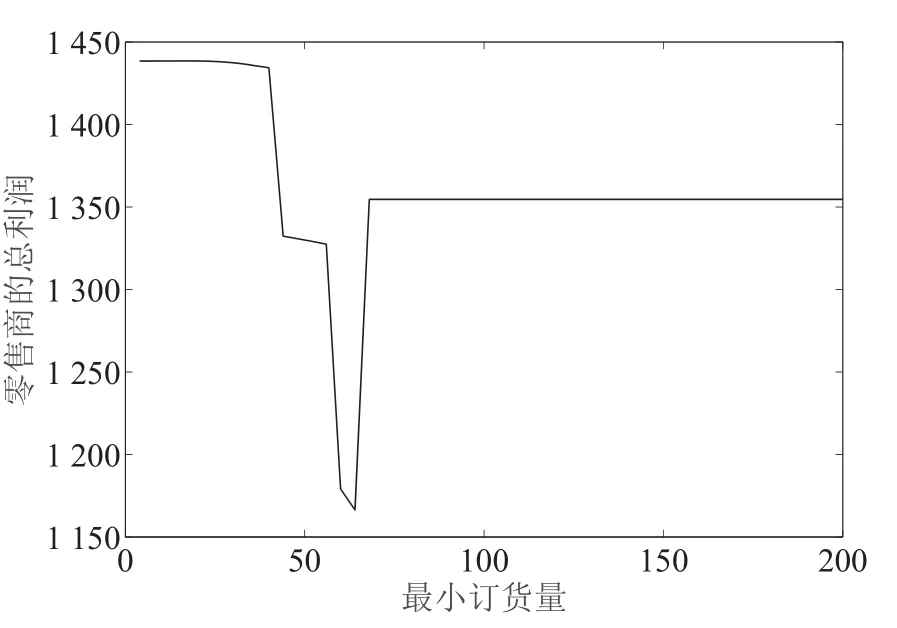
圖1 產(chǎn)品1 最小訂貨量對利潤的影響Fig.1 The profit affected by minimum order quantity of product 1

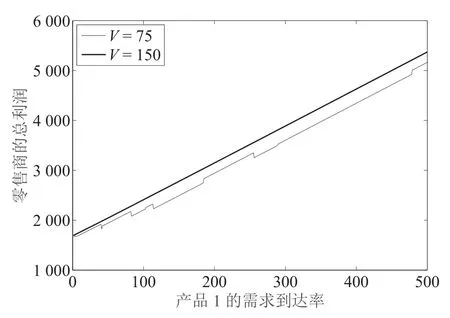
圖2 產(chǎn)品1 需求對總利潤的影響Fig.2 The total profit affected by demand arrive rate of product 1

通過上面的數(shù)值實驗得到的結論是,在一定范圍內(nèi),零售商的利潤與庫存容量和需求到達率正相關.

5.2 聯(lián)合采購的算例分析

本節(jié)主要研究產(chǎn)品種類,庫存容量和聯(lián)盟規(guī)模對聯(lián)盟合作收益的影響.本節(jié)的部分參數(shù)值取一定范圍的隨機數(shù),其取值范圍為λji ∈[1,25],pi ∈[5,50],ci=另外h=1,Vi=75,i ∈N.

首先研究產(chǎn)品種類數(shù)量和庫存容量對聯(lián)盟利潤的影響.|M|=10,產(chǎn)品種類數(shù)量|N|分別取5,10,20,50,100,500,為方便計算,所有零售商的庫存容量取一樣的值,其值分別取75,150,300,600.產(chǎn)品種類和庫存容量各取一個值,h=1,其它參數(shù)隨機產(chǎn)生,計算合作后利潤增長比率,每一組做100 次,取平均值,得到表3.將表3 中的數(shù)據(jù)縱向對比,可以看到,當產(chǎn)品種類為5 和10 時,庫存容量增大并沒有幫助聯(lián)盟獲得更大收益,而產(chǎn)品種類大于20 時,聯(lián)盟收益隨庫存容量增大而增大.這是因為產(chǎn)品種類為5 和10 時,庫存容量總是充足的,所以增加庫存容量并不能幫助聯(lián)盟提高收益.而產(chǎn)品種類大于20 時,庫存容量不足導致每次采購量受限,增加了采購頻率,從而增加了成本.當庫存容量增大時能夠幫助聯(lián)盟減小成本二獲得更高收益.然后進行橫向對比,觀察表3 中每一行的數(shù)據(jù),可以看到,每一行從左到右,聯(lián)盟的利潤增長率整體都是呈下降趨勢的.這是因為當產(chǎn)品種類很多時,零售商的選擇更廣了,尤其當庫存容量不足時,產(chǎn)品種類越多,選擇相同的產(chǎn)品概率就越低.在極端情況下甚至可能所有的零售商都采購不同的產(chǎn)品,從而無法形成聯(lián)合采購.

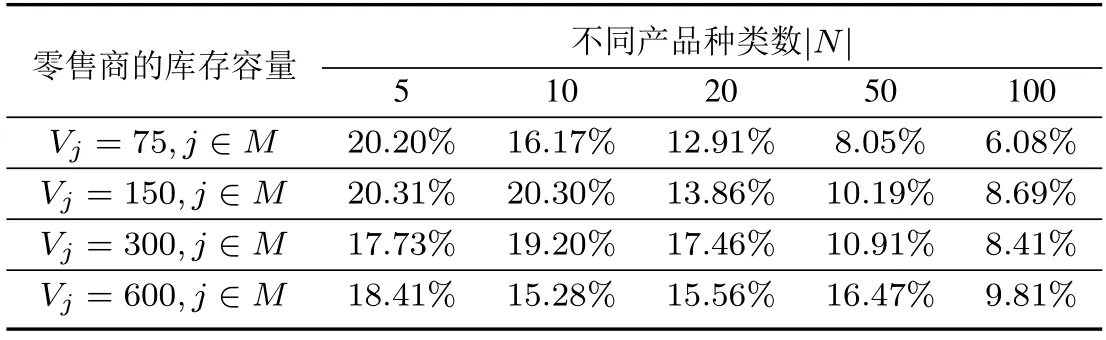
表3 產(chǎn)品種類數(shù)量和庫存容量對聯(lián)盟收益的影響Table 3 The profit affected by product category quantity and inventory capacity

接下來研究聯(lián)盟規(guī)模對聯(lián)盟收益的影響.聯(lián)盟成員數(shù)|M|分別取5, 10, 20, 50, 100, 500,h= 1,Vj=150,j ∈M,|N|= 10,100,其它數(shù)據(jù)隨機產(chǎn)生,同樣每組做100 次,聯(lián)盟利潤增長率取平均值,得到表4 的數(shù)據(jù).可以觀察到表4 中聯(lián)盟利潤增長率是隨聯(lián)盟規(guī)模增大而增大的.通過表4 可以看到僅有產(chǎn)品種類為100,聯(lián)盟成員數(shù)為5 時,才存在聯(lián)盟庫存容量使用完以及零售商出現(xiàn)負增長的情況,而其它情況下庫存容量總是有剩余的.而定理2 證明了庫存容量充足,并且最優(yōu)訂購量大于供應商的最小訂貨量的情況下,本文的分配方案總是在聯(lián)合采購博弈的核中的.這也意味著當聯(lián)盟規(guī)模較大并且聯(lián)盟成員采購的產(chǎn)品高度集中(有較多的零售商采購同一種產(chǎn)品)時,總是能夠保證設計的分配方案是核分配方案,因為聯(lián)盟規(guī)模較大時更容易達到供應商最小訂貨量要求.并且當采購產(chǎn)品種類比較小時,會有更多的零售商采購同一種產(chǎn)品,能夠節(jié)省更多的庫存容量.

表4 聯(lián)盟規(guī)模對收益的影響Table 4 The profit affected by coalition scale

通過上面的實驗,可以看到,產(chǎn)品種類越少,庫存容量越大,聯(lián)盟成員越多,聯(lián)合采購提高的利潤越多;聯(lián)合采購最高可以提高聯(lián)盟總利潤的26%.并且可以看到零售商數(shù)量大于10 時,再也沒出現(xiàn)庫存容量不夠的情況了,這說明參與合作的零售商較多時,聯(lián)盟出現(xiàn)庫存容量不夠的概率較小.

這些數(shù)值實驗都是使用MATLAB 2015b 實現(xiàn)的.通過MATLAB 計時函數(shù)tic 和toc, 算法1 求解10 000 種產(chǎn)品的單獨采購決策模型只需要27 s, 而算法2 求解10 000 種產(chǎn)品, 100 個零售商的聯(lián)合采購模型也只需大概660 s 完成.這說明算法1 和算法2 的效率是非常高的,能夠滿足比較大規(guī)模的計算要求.

6 結束語

本文研究了庫存容量和最小訂貨量約束的產(chǎn)品選擇和聯(lián)合采購問題.首先建立了一個多產(chǎn)品選擇的模型,通過該模型零售商單獨決策需要購進哪些產(chǎn)品以及其購進量.然后設計了一個多項式時間算法求解該模型,并證明了在文中給定的三種情況下該算法得到的解是最優(yōu)解.為了幫助中小型企業(yè)提高利潤,建立了庫存共享下的聯(lián)合采購決策模型并證明了該模型能夠提高合作聯(lián)盟的總利潤.為激勵零售商形成合作聯(lián)盟,分別為聯(lián)盟庫存容量充足的情況下設計了核分配方案和聯(lián)盟庫存容量不足的情況下設計了滿足個人理性的有效分配方案.數(shù)值實驗表明聯(lián)合采購總是能夠提高聯(lián)盟的利潤并且當參與合作的零售商越多,合作聯(lián)盟提高的利潤越高.

本文的一些假設一定程度上限制了模型的應用.首先假設零售商采用統(tǒng)一零售價進行銷售,這限制了聯(lián)合采購產(chǎn)品的種類,對于許多產(chǎn)品零售商會選擇自主定價.其次在資源限制中并沒有考慮資金限制,并且在聯(lián)合采購模型中,并沒有考慮庫存共享時產(chǎn)生的轉運成本.這幾個因素會使模型更加的復雜和難解,但也會更貼近現(xiàn)實,是值得繼續(xù)深入研究的.