浙江省寧波效實中學(xué)(315012)童益民

立體幾何中三面角內(nèi)面角的大小及變化規(guī)律在動態(tài)中是一個比較難理解的問題,在高考與模擬考中也經(jīng)常出現(xiàn),學(xué)生對此類問題往往有錯誤的認(rèn)識,總認(rèn)為二面角的平面角大于相對的面角,并認(rèn)為面角是單向變化的,解題上也是往往束手無策,本文試圖通過三面角余弦定理與函數(shù)的思想解決這一系列問題.

三面角余弦定理如圖1,由射線PA,PB,PC構(gòu)成的三面角P?ABC中,∠APC=α,∠BPC=β,∠APB=γ,二面角A?PC?B的大小為θ,則cosγ=cosαcosβ+sinαsinβcosθ.(證明可見參考文獻[1])

圖1

問題一.當(dāng)θ 變化時,研究γ 與θ 的大小關(guān)系

題目1如圖2,已知ΔABC,D是AB的中點,沿直線CD將ΔACD翻折成ΔA1CD,所成二面角A1?CD?B的平面角為θ,則( )(選自2015年浙江高考理科第8 題)

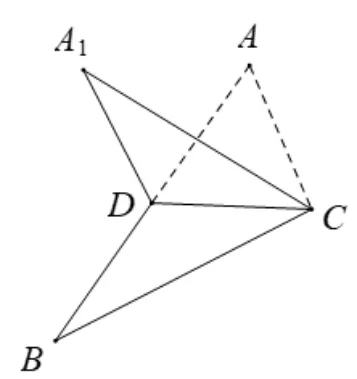
圖2

A.∠A1DB≤θB.∠A1DB≥θ

C.∠A1CB≤θD.∠A1CB≥θ

解法2(不通過結(jié)論1)如圖3,作AO⊥CD于O點,延長交BC于E點,連接A1O,A1A.因為OE⊥CD,所以∠A1OE是二面角A1?CD?B的平面角,即∠A1OE=θ.因為A1D=AD≥A1O=AO,所以∠A1DA≤ ∠A1OA,所以∠A1DB≥ ∠A1OE,即∠A1DB≥θ,所以答案B 是正確的.而∠A1CB與θ的大小關(guān)系是不確定的,當(dāng)θ=0 時,∠A1CB≥θ;當(dāng)θ=π時,∠A1CB <θ.

圖3

小結(jié)從題目1 的解法2 中,我們可以發(fā)現(xiàn),不通過結(jié)論1 也可以很好的把題目解決,但需要特殊情況來排除,對面角與相對二面角的大小關(guān)系的整體情況,還是沒有深刻的體會,但通過三面角余弦定理,可以對該類問題有清楚深刻的理解.知道了面角γ與相對的二面角的平面角θ的大小關(guān)系,接下來更難的是要弄清楚當(dāng)二面角的大小θ固定,而α,β變化時,面角γ的變化規(guī)律是怎樣的?

問題二.當(dāng)α,β 變化時,研究γ 的變化規(guī)律

如圖4,由射線PA,PB,PC構(gòu)成的三面角P?ABC中,∠APC=α,∠BPC=β,α,β∈∠APB=γ,二面角A?PC?B的大小為θ,若AC⊥PC,BC⊥PC,則∠ACB=θ,當(dāng)α,β變化,即PC的長度變化時,研究γ的變化規(guī)律.

圖4

因為當(dāng)PC的長度變化時,α與β是關(guān)聯(lián)的,但它們之間的關(guān)系很難表示出來,所以用三面角余弦定理cosγ=cosαcosβ+ sinαsinβcosθ,很難用角α或β來研究角γ,所以引入新的變量PC.

圖5

圖6

圖7

圖8

圖9

解析 ①是正確的,在此不作分析.②是錯誤的,因為假設(shè)AC=AD,BC=BD時,取CD中點M,則二面角A?CD?B的平面角為∠AMB,如圖10.根據(jù)結(jié)論2,當(dāng)∠AMB比較小時,P點從M點到C點,∠APB可先變大再變小,即可以∠AMB≤θ <∠ACB,同樣也可以∠AMB≤θ <∠ADB,所以可以θmin=∠AMB,而不一定是θmin=min{∠ACB,∠ADB},這樣②是錯誤的,答案為A.

圖10

總結(jié)題目2 中要得到∠APB的最小值是一個比較復(fù)雜的問題,首先要清楚的知道∠APB的變化規(guī)律,不要錯誤的認(rèn)為P點從C點到D點,∠APB是單向變化的,或者錯誤的認(rèn)為P點從M點到C(或D)點,∠APB是逐漸變小的.根據(jù)結(jié)論2,∠APB的變化規(guī)律不一定是單向的,根據(jù)不同的條件會有不同的變化規(guī)律,如果沒有對問題二有非常清楚的認(rèn)識,恐怕很難理解這道題目.