Hadamard MDS 矩陣的一種快速搜索算法*

王 石, 李云青, 徐運(yùn)閣, 曾祥勇

湖北大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院應(yīng)用數(shù)學(xué)湖北省重點(diǎn)實(shí)驗(yàn)室, 武漢 430062

1 引言

擴(kuò)散和混淆是Shannon 提出的設(shè)計(jì)對(duì)稱(chēng)密碼體制的兩種基本方法[1], 其目的是為了抵抗攻擊者對(duì)密碼體制的統(tǒng)計(jì)分析. 擴(kuò)散層可以通過(guò)線(xiàn)性擴(kuò)散矩陣實(shí)現(xiàn), 而矩陣的擴(kuò)散能力通常由其分支數(shù)量化. 當(dāng)分支數(shù)達(dá)到最大時(shí), 將該矩陣稱(chēng)為MDS 矩陣. 由于MDS 矩陣具有最大的分支數(shù)可以有效的抵抗差分分析[2]和線(xiàn)性分析[3]. 因此, 1998 年Rijmen 等人首次將MDS 矩陣應(yīng)用到Rijndael 算法中, 即高級(jí)加密標(biāo)準(zhǔn)(AES)[4]. 此后, MDS 矩陣被廣泛的應(yīng)用到線(xiàn)性層的設(shè)計(jì)中.

構(gòu)造MDS 矩陣的方法主要有兩種. 文獻(xiàn)[5–7]中, 作者利用線(xiàn)性操作, 以字為單位直接構(gòu)造具有高效實(shí)現(xiàn)電路的MDS 矩陣. 此外, 在特殊的子類(lèi)中構(gòu)造也是MDS 矩陣的常見(jiàn)構(gòu)造方法, 如利用循環(huán)矩陣[8–11]和Hadamard 矩陣[12–14]. 文獻(xiàn)[10]指出, 循環(huán)矩陣可以通過(guò)迭代的方式實(shí)現(xiàn), 在資源受限的環(huán)境中能有效地提高硬件效率. 而Hadamard 矩陣不僅可以通過(guò)迭代的方式實(shí)現(xiàn), 同時(shí)也容易構(gòu)造具有對(duì)合性質(zhì)的MDS 矩陣[6,11,15,16]. 因此, 在設(shè)計(jì)密碼算法時(shí), 研究者們經(jīng)常會(huì)考慮使用Hadamard MDS 矩陣作為擴(kuò)散層.

檢驗(yàn)MDS 性質(zhì)是構(gòu)造MDS 矩陣的關(guān)鍵步驟之一. 文獻(xiàn)[17]給出了MDS 矩陣的等價(jià)定義, 即一個(gè)矩陣為MDS 矩陣當(dāng)且僅當(dāng)其任意階的子方陣滿(mǎn)秩. 因此, 可以通過(guò)判斷矩陣所有子方陣的行列式是否非零來(lái)確定MDS 性質(zhì). 高斯消元法是計(jì)算行列式最常用的方法, 利用高斯消元法計(jì)算一個(gè)n階矩陣的行列式的復(fù)雜度為O(n3). 隨著矩陣的階數(shù)的增加, 計(jì)算單個(gè)子方陣的行列式的復(fù)雜度也會(huì)隨之上升. 而文獻(xiàn)[18]給出了一種新的MDS 矩陣的判別方法, 將一個(gè)矩陣所有子矩陣行列式的乘積分解為若干個(gè)不可約多項(xiàng)式, 不可約多項(xiàng)式的集合即為判別MDS 矩陣的條件集. 若集合中任意元素均可逆, 則可判定該矩陣為MDS 矩陣.

本文主要研究Hadamard MDS 矩陣的搜索方法. 首先給出了一種新的MDS 矩陣的判定方法稱(chēng)為鏈?zhǔn)脚袆e法, 其主要思想是按階數(shù)由低到高的順序計(jì)算子方陣行列式, 將獲得的k階子方陣的行列式存放在一張表中, 在計(jì)算k+1 階子方陣行列式時(shí)直接從存儲(chǔ)表中調(diào)用k階子方陣的行列式進(jìn)行計(jì)算. 由此, 單個(gè)子方陣行列式的計(jì)算復(fù)雜度為O(n). 相比較之前的方法, 判定矩陣MDS 性質(zhì)的速度有了很大提升. 其次, 對(duì)于4 階Hadamard 矩陣M, 利用對(duì)稱(chēng)多項(xiàng)式基本定理, 證明出了M任意子方陣的行列式均可用初等對(duì)稱(chēng)多項(xiàng)式表示. 基于此, 給出了4 階Hadamard MDS 矩陣的判定定理. 此外, 利用代數(shù)余子式, 本文給出了8 階Hadamard MDS 矩陣的判定方法. 只需證明其i(i ≤4) 階子方陣均滿(mǎn)秩即可判定該矩陣為MDS 矩陣. 利用上述判別方法, 搜索出了有限域F24和F26所有4 階及8 階的Hadamard MDS 矩陣,并且找到了有限域F2n(n ≤16) 上實(shí)現(xiàn)代價(jià)最低的Hadamard MDS 矩陣. 最后, 為了進(jìn)一步提高搜索的效率, 本文建立了有限交換環(huán)上4 階Hadamard 矩陣和有限域上8 階Hadamard 矩陣之間的聯(lián)系, 利用該聯(lián)系可以快速過(guò)濾不滿(mǎn)足MDS 性質(zhì)的Hadamard 矩陣.

2 預(yù)備知識(shí)

本節(jié)主要介紹MDS 矩陣以及Hadamard 矩陣的相關(guān)概念. 首先給出本文中常用的符號(hào), 見(jiàn)表1.

表1 符號(hào)說(shuō)明Table 1 Notations

定義1[19]設(shè)M是一個(gè)m階非奇異方陣,M的伴隨矩陣定義為

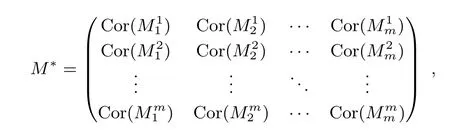
根據(jù)該定理,M的行列式可由其m ?1 階子方陣的行列式計(jì)算得到. 下面介紹MDS 矩陣的概念.

定義2[4]M為MDS 矩陣當(dāng)且僅當(dāng)M的任意階子方陣都是可逆的.

根據(jù)該定義, 若一個(gè)矩陣的所有子方陣行列式均不為0, 則該矩陣為MDS 矩陣.

定義3[10]設(shè)矩陣P是一個(gè)m階方陣, 若P的每一行每一列都恰有一個(gè)1 且其余元素均為0, 則稱(chēng)P為置換矩陣.

命題1[10,11]設(shè)P1,P2是兩個(gè)置換矩陣, 矩陣M是MDS 矩陣當(dāng)且僅當(dāng)P1MP2是MDS 矩陣.

置換矩陣僅改變矩陣行列的位置, 不改變子矩陣的可逆性. 因此, 將M與置換矩陣相乘不改變其MDS 性質(zhì).

定義4[15]若H為有限域F2n上的2s階Hadamard 矩陣, 它可以由兩個(gè)Hadamard 子方陣表示:

該矩陣可記作H=Had(a1,a2,··· ,a2s), 其中a1,a2,··· ,a2s為Hadamard 矩陣的首行元素.

關(guān)于Hadamard 矩陣, 有如下性質(zhì).

命題2[20]設(shè)H=Had(a1,a2,··· ,a2s) 為有限域F2n上的一個(gè)2s階Hadamard 矩陣, 則

下面引入Hadamard 等價(jià)矩陣的概念.

定義5[10,14]設(shè)P1,P2是兩個(gè)置換矩陣, 若矩陣M和P1MP2是兩個(gè)Hadamard 矩陣, 則稱(chēng)P1MP2是M的Hadamard 等價(jià)矩陣, 記作M ～H P1MP2.

命題3設(shè)P1,P2是兩個(gè)置換矩陣,M是F2n上的m階Hadamard 矩陣. 若M和P1MP2是Hadamard 等價(jià)矩陣, 則M和P1MP2有相同的i階子方陣, 其中1≤i ≤m ?1.

因此, 根據(jù)Hadamard 矩陣的首行元素的個(gè)數(shù), 我們即可確定Hadamard 等價(jià)類(lèi)的個(gè)數(shù).

注1設(shè)S是一個(gè)由2s個(gè)非零元素構(gòu)成的集合, 其中S={a1,a2,··· ,a2s}.

(1) 當(dāng)2s=4 時(shí), 根據(jù)命題4可知由集合S中的元素構(gòu)成的Hadamard 矩陣僅有1 個(gè)等價(jià)類(lèi);

(2) 當(dāng)2s=8 時(shí), 根據(jù)命題4可知由集合S中的元素構(gòu)成的Hadamard 矩陣可分為30 個(gè)等價(jià)類(lèi);

(3) 設(shè)S是由8 個(gè)非零元構(gòu)成的集合,H為Hadamard 矩陣, 其中S={a1,a2,··· ,a8}且H=Had(a1,a2,··· ,a8). 對(duì)于集合S中任意三個(gè)元素ai1,ai2,ai3, 總存在一個(gè)Hadamard 矩陣H′=Had(ai1,ai2,··· ,αi8) 使得H ～H H′, 其中{ai1,ai2,··· ,αi8}={a1,a2,··· ,a8}.

命題5[21]若A,B,C,D均為同階方陣, 則

3 MDS 矩陣的鏈?zhǔn)脚袆e法

由定義2可知, 判定MDS 矩陣時(shí), 需要檢驗(yàn)其所有子方陣是否滿(mǎn)秩. 最常見(jiàn)的方法是利用高斯消元計(jì)算矩陣的行列式, 若所有子方陣行列式均不為0, 則該矩陣為MDS 矩陣. 然而, 隨著矩陣階數(shù)增大, 待計(jì)算的行列式的個(gè)數(shù)會(huì)急劇增加. 因此, 判定過(guò)程將更加耗時(shí). 我們提出了一種更高效的判別方法, 根據(jù)定理1 中行列式的計(jì)算方法, 將低階矩陣的行列式的值儲(chǔ)存用于計(jì)算高階矩陣的行列式, 實(shí)現(xiàn)資源的重復(fù)利用, 從而減小計(jì)算量.

3.1 建立鏈?zhǔn)奖?/h3>

設(shè)M為有限域F2n上的m階方陣,表示M的一個(gè)k階子方陣. 由定理1 知k階矩陣的行列式可以通過(guò)k ?1 階行列式計(jì)算, 其中1≤k ≤m. 若k ?1 階行列式已知, 則k階行列式的計(jì)算過(guò)程將被有效地簡(jiǎn)化. 因此, 我們按照階數(shù)由低到高的順序計(jì)算子方陣的行列式, 將階數(shù)相同的子方陣行列式的值存儲(chǔ)到同一表中, 并在后續(xù)計(jì)算階數(shù)更大的矩陣時(shí)調(diào)用表中行列式的值.

令S(k,m)表示元素小于等于m的k維向量構(gòu)成的集合, 其中向量元素按由小到大的順序排列:

下面介紹建表過(guò)程:

注意, 我們研究的是特征為2 的有限域上MDS 矩陣的判定. 此時(shí), 矩陣的代數(shù)余子式與余子式相同,故可直接代入低階行列式的值計(jì)算階數(shù)更大的行列式. 當(dāng)特征不為2 時(shí), 還需考慮行列式的符號(hào).

下面我們給出一個(gè)例子具體說(shuō)明如何通過(guò)建表來(lái)判斷矩陣的MDS 性質(zhì).

例1M為有限域F24/(x4+x+1) 上的4 階方陣,

其中1 表示為有限域上的單位元,α為多項(xiàng)式x4+x+1 的一個(gè)根. 由于M為4 階方陣, 我們可以確定其2 階和3 階子方陣行(列) 指標(biāo)的向量集合.

顯然,M的1 階子方陣均不為0. 下面建立2 階行列式存儲(chǔ)表T2. 首先令r=1,c=1 計(jì)算T2[1,1].由于f2(1)?1=[1,2], 對(duì)應(yīng)行指標(biāo)為[1,2] 列指標(biāo)也為[1,2]. 因此,

利用上述方法遍歷r,c(1≤r,c ≤6), 依次計(jì)算T3[r,c] 的值, 結(jié)果見(jiàn)圖1.

圖1 2 階行列式存儲(chǔ)表Figure 1 Storage table of 2-order determinants

利用上述方法遍歷r,c(1≤r,c ≤4), 依次計(jì)算T3[r,c] 的值, 結(jié)果見(jiàn)圖2.

圖2 3 階行列式存儲(chǔ)表Figure 2 Storage table of 3-order determinants

最后, 利用表T3中3 階行列式的值計(jì)算矩陣M的行列式.r3=f3([1,2,3])=1,c1=f3([1,2,3])=1,c2=f3([1,2,4])=2,c3=f3([1,3,4])=3,c4=f3([2,3,4])=4. 由定理1 可得

綜上,M所有子方陣行列式均不為零, 故為MDS 矩陣.

3.2 MDS 矩陣的判定方法

由行列式儲(chǔ)存表, 我們給出MDS 矩陣的鏈?zhǔn)脚袆e法. 設(shè)矩陣M是一個(gè)m階方陣, 首先判斷M是否存在零元素. 若元素全為非零元, 則建立2 階行列式存儲(chǔ)表T2. 若T2中元素均不為0, 則利用表T2中的結(jié)果建立3 階行列式存儲(chǔ)表T3. 類(lèi)似地, 依次由k ?1 階行列式存儲(chǔ)表, 計(jì)算Tk, 直至求得m階方陣行列式的值. 若在建表過(guò)程中存在某子方陣行列式為0, 則判定結(jié)束, 該矩陣不是MDS 矩陣. 具體過(guò)程見(jiàn)算法1.

算法1 MDS 矩陣的鏈?zhǔn)脚袆e法Input: m×m 矩陣M.Output: 若返回值為1 則M 是MDS 矩陣, 否則不是MDS 矩陣.1 初始化: 集合S(k,m) 及對(duì)應(yīng)函數(shù)fk, k 階行列式存儲(chǔ)表Tk ←0, k = 2,3,··· ,m;2 for 1 階行列式Mij(1 ≤i,j ≤m) do return 0;5end 6 end 7 for 2 階行列式1 ≤r,c ≤C2m do 3if 1 階行列式Mij == 0 then 4 8計(jì)算r,c 所對(duì)應(yīng)的行列指標(biāo)f?1 2 (r) = [i1,i2],f?1 2 (c) = [j1,j2];9計(jì)算2 階行列式T2[r,c] =■■■M[i1,i2][j1,j2]■■■= Mi1 j1 Mi2 j2 +Mi1j2 Mi2 j1;10if 2 階行列式T2[r,c] == 0 then 11return 0;12end 13 end 14 for k 階行列式存儲(chǔ)表3 ≤k ≤m do 15for k 階行列式1 ≤r,c ≤Ckm do k (r) = [i1,i2,··· ,ik],f?1k (c) = [j1,j2,··· ,jk];17計(jì)算rk?1 = fk?1([i1,i2,··· ,ik?1]), cs = fk?1([j1,j2,··· ,jk]/[js]), s = 1,2,··· ,k;18計(jì)算k 階行列式Tk[r,c] = ∑k s=1 Mikjs Tk?1[rk?1,cs];19if k 階行列式Tk[r,c] == 0 then 16計(jì)算r,c 所對(duì)應(yīng)的行列指標(biāo)f?1 20return 0;21end 22end 23 end 24 return 1;

我們將鏈?zhǔn)脚袆e法與高斯消元法判斷MDS 矩陣所需的計(jì)算量進(jìn)行對(duì)比. 由表2 可知, 隨著矩陣階數(shù)增大, 兩種方法所需計(jì)算量差異也逐漸增大. 以8×8 矩陣為例, 使用高斯消元法所需乘法運(yùn)算數(shù)是鏈?zhǔn)脚袆e法的6.8 倍, 所需加法運(yùn)算數(shù)是鏈?zhǔn)脚袆e法的8 倍. 顯然, 使用鏈?zhǔn)脚袆e法來(lái)判定MDS 矩陣能夠有效地提升計(jì)算效率.

表2 計(jì)算量對(duì)比Table 2 Comparisons of computational complexity

4 Hadamard MDS 矩陣的判定方法

在對(duì)稱(chēng)密碼算法中, 通常會(huì)使用一些特殊類(lèi)型的矩陣作為擴(kuò)散層. 結(jié)合矩陣自身的特殊性質(zhì), MDS 性質(zhì)的判別方法會(huì)更加簡(jiǎn)單. 本節(jié)將介紹有限域中Hadamard MDS 矩陣的判定方法.

4.1 有限域中4 階Hadamard MDS 矩陣的判定方法

本小節(jié)給出了有限域F2n上4 階Hadamard MDS 矩陣的判定方法. 我們引入對(duì)稱(chēng)多項(xiàng)式的概念.

定義6[24]設(shè)多項(xiàng)式f ∈R[a1,a2,··· ,an]. 若對(duì)于整數(shù)1,2,··· ,n的任意置換i1,i2,··· ,in都有多項(xiàng)式f(ai1,ai2,··· ,ain)=f(a1,a2,··· ,an), 則稱(chēng)f為對(duì)稱(chēng)多項(xiàng)式. 其中

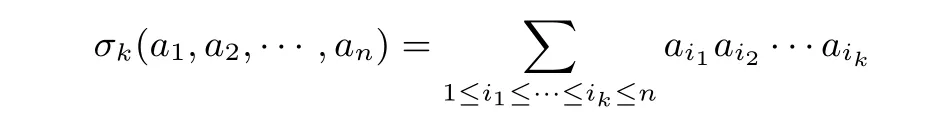
稱(chēng)為R[a1,a2,··· ,an] 上的k次初等對(duì)稱(chēng)多項(xiàng)式.

下面介紹對(duì)稱(chēng)多項(xiàng)式基本定理.

定理 2[24]對(duì)于任意對(duì)稱(chēng)多項(xiàng)式f ∈ R[a1,a2,··· ,an], 存在唯一確定的多項(xiàng)式h ∈R[a1,a2,··· ,an] 使得f(a1,a2,··· ,an)=h(σ1,σ2,··· ,σn).

我們可以將4 階Hadamard 矩陣子方陣行列式的乘積表示為置換多項(xiàng)式.

例2設(shè)M=Had(1,a,a+1,((a+1)a)?1) 是有限域F2n上的4×4 Hadamard 矩陣, 其中1,a,a+1,((a+1)a)?1是有限域中的4 個(gè)互不相同的非零元并且n是一個(gè)奇數(shù), 則M是MDS 矩陣.

4.2 交換環(huán)上4 階Hadamard MDS 矩陣的判定方法

這一小節(jié), 我們將有限域中的4 階Hadamard MDS 矩陣判定定理3 推廣到特征為2 的交換環(huán)上. 首先定義交換環(huán)上的MDS 矩陣.

定義7[22]設(shè)M是偶特征交換環(huán)上的4 階矩陣. 若M任意階子方陣行列式的值都是可逆矩陣, 則稱(chēng)M是4 階MDS 矩陣.

類(lèi)似命題6 的證明方法, 可以得到如下結(jié)論:

則M 是一個(gè)特征為2 的交換環(huán).

證明:集合M 中的元素為2 階Hadamard 矩陣且矩陣元素屬于有限域F2n. 有限域F2n上2 階Hadamard 矩陣關(guān)于加法運(yùn)算可交換, 關(guān)于乘法運(yùn)算封閉, 且滿(mǎn)足結(jié)合律和分配律, 由此可知M 是一個(gè)環(huán). 根據(jù)命題2, 對(duì)于任意兩個(gè)2 階Hadamard 矩陣H1,H2∈M 均滿(mǎn)足H1H2=H2H1. 因此, 環(huán)M 對(duì)乘法滿(mǎn)足交換性. 對(duì)于M 中任意元素H=Had(a1,a2),

即M 的特征為2. 綜上可得集合M 是一個(gè)特征為2 的交換環(huán).

4.3 8 階Hadamard MDS 矩陣的判定方法

本節(jié)將利用Hadamard 矩陣的性質(zhì), 給出8 階Hadamard MDS 矩陣的判定方法.

命題8設(shè)M= Had(a1,a2,··· ,a8) 是一個(gè)8 階非奇異Hadamard 矩陣, 其中ai(1≤i ≤8) 為有限域F2n中的非零元, 則M的所有7 階子方陣均為非奇異矩陣.

下面介紹8 階Hadamard 矩陣的2 階子方陣與6 階子方陣的關(guān)系.

命題9設(shè)M= Had(a1,a2,··· ,a8) 是一個(gè)8 階非奇異Hadamard 矩陣, 其中ai(1≤i ≤8) 為有限域F2n中的非零元素. 若M的任一2 階子方陣非奇異, 則M的任一6 階子方陣也為非奇異矩陣.

證明:對(duì)于矩陣M, 2 階子方陣的余子式為6 階子方陣的行列式. 因此, 我們可以將判定6 階子方陣的滿(mǎn)秩問(wèn)題轉(zhuǎn)化為判定2 階子方陣余子式是否為0 的問(wèn)題.

其中A,B,C,D均為有限域F2n上的4 階方陣且B,D為Hadamard 矩陣. 由Hadamard 矩陣的交換性得BD=DB. 根據(jù)命題2, 利用公式|M3|=|DA ?BC| 計(jì)算分塊矩陣行列式得

對(duì)該行列式進(jìn)行列變換(第1 列加到第4 列, 第2 列加到第3 列)得

下面給出8 階Hadamard 矩陣3 階子方陣與5 階子方陣的關(guān)系.

命題10設(shè)M=Had(a1,a2,··· ,a8) 是一個(gè)8 階非奇異Hadamard 矩陣, 其中ai(1≤i ≤8) 為有限域F2n中的非零元素. 若M的任一3 階子方陣非奇異, 則M的任一5 階子方陣也為非奇異矩陣.

計(jì)算該矩陣的行列式得

因?yàn)镃,D是Hadamard 矩陣滿(mǎn)足CD=DC, 由命題2可得|M2|=|AD ?BC|, 即

根據(jù)上述結(jié)論, 我們可以給出判定8 階Hadamard MDS 矩陣的充要條件.

定理5設(shè)M= Had(a1,a2,··· ,a8) 是一個(gè)8 階非奇異Hadamard 矩陣, 其中ai(1≤i ≤8) 是有限域F2n中的非零元素. 若M的i(i ≤4) 階子方陣均為非奇異矩陣, 則M是一個(gè)Hadamard MDS 矩陣.

證明:由命題8可得, 當(dāng)M的所有元素均不為0 時(shí),M的所有7 階子方陣也都是非奇異矩陣. 若M的所有2 階子方陣均為非奇異矩陣, 由命題9知M的所有6 階子方陣也為非奇異矩陣. 若M的所有3 階子方陣均為非奇異矩陣, 由命題10知M的所有5 階子方陣均為非奇異矩陣. 綜上, 若M的i(i ≤4)階子方陣均為非奇異矩陣, 則M的任意階子方陣均為非奇異矩陣, 可得M是一個(gè)Hadamard MDS 矩陣.

因此, 若要判斷一個(gè)8 階Hadamard 矩陣的MDS 性質(zhì), 只需計(jì)算所有i(i ≤4) 階子方陣行列式是否為0, 若均不為0, 則該Hadamard 是MDS 矩陣, 反之不是.

5 Hadamard MDS 矩陣的搜索

基于上述Hadamard MDS 矩陣的判定方法, 我們可以對(duì)Hadamard MDS 矩陣進(jìn)行搜索. 本節(jié)首先給出有限域F2n上4 階和8 階Hadamard MDS 矩陣的搜索方法. 然后, 利用有限域和有限交換環(huán)的關(guān)系, 進(jìn)一步優(yōu)化8 階Hadamard MDS 矩陣的搜索方法.

5.1 4 階Hadamard MDS 矩陣的搜索

首先給出有限域F2n上4 階Hadamard MDS 矩陣的搜索算法. 由定理3 可知, 判定一個(gè)4階Hadamard 矩陣Had(a1,a2,a3,a4)是否為MDS 矩陣需計(jì)算σ1,σ21σ4+σ23, 其中σ1,σ3,σ4為F2n[a1,a2,a3,a4] 上的初等對(duì)稱(chēng)多項(xiàng)式. 下面給出σ1,σ3,σ4的計(jì)算過(guò)程:

利用上述判定方法, 只需在有限域F2n{0}上遍歷首行元素a1,a2,a3,a4再判斷MDS 性質(zhì), 即可搜索4 階Hadamard MDS 矩陣. 我們使用文獻(xiàn)[23] 中的度量方法計(jì)算矩陣的實(shí)現(xiàn)代價(jià), 在不同的有限域中搜索并找到了該度量方法下代價(jià)最低的4 階Hadamard MDS 矩陣, 結(jié)果見(jiàn)表3.

之前的研究者也嘗試尋找在不同的有限域中獲得的異或數(shù)最低的4 階Hadamard MDS 矩陣. 我們也將其羅列在表3 并給出相應(yīng)的參考文獻(xiàn).

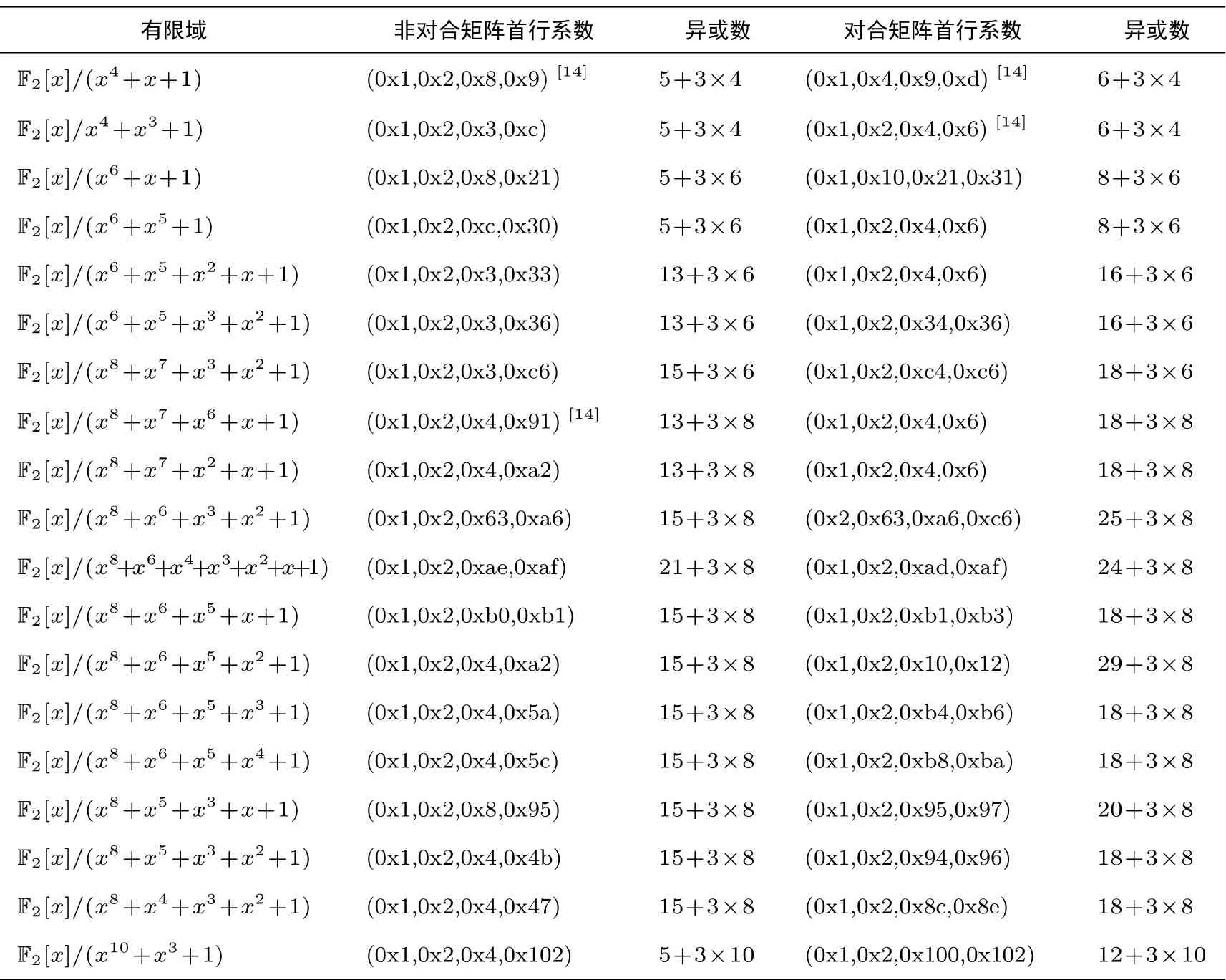
表3 不同有限域中的異或數(shù)最低的4 × 4 Hadamard MDS 矩陣Table 3 4 × 4 Hadamard MDS Matrices with lowest xor in different finite fields

5.2 8 階Hadamard MDS 矩陣的搜索

由命題1易知, 同一Hadamard 等價(jià)類(lèi)的矩陣有相同的MDS 性質(zhì). 因此, 我們只需要從每個(gè)等價(jià)類(lèi)中選擇1 個(gè)矩陣檢驗(yàn)它是否為MDS 矩陣即可確定對(duì)應(yīng)Hadamard 等價(jià)類(lèi)的MDS 性質(zhì). 8 階Hadamard矩陣一共有30 個(gè)等價(jià)類(lèi), 代表矩陣如表4 所示. 下面我們給出有限域F2n上8 階Hadamard MDS 矩陣的搜索方法.

表4 30 個(gè)Hadamard 矩陣的等價(jià)類(lèi)Table 4 30 equivalent representations of Hadamard matrices

首先, 從有限域F2n的2n ?1 個(gè)非零元素中選擇8 個(gè)互不相同的元素a1,a2,··· ,a8. 此時(shí)一共有種選擇. 對(duì)于每一次選擇的8 個(gè)元素, 都有30 個(gè)不同的等價(jià)類(lèi). 我們利用4.3 節(jié)給出的8 階Hadamard MDS 矩陣判定方法, 來(lái)驗(yàn)證每一個(gè)等價(jià)代表矩陣是否為MDS 矩陣. 若判定對(duì)合HadamardMDS 矩陣則需要判斷8 個(gè)元素之和是否為1. 如果不為1 則需要重新選擇元素. 最終, 我們?cè)谟邢抻騀24中搜索到15 個(gè)8 階Hadamard MDS 矩陣, 在有限域F26中搜索到約20 萬(wàn)個(gè)對(duì)合Hadamard MDS 矩陣.該方法還可以在更大的有限域F2n(n ≤16) 中尋找實(shí)現(xiàn)代價(jià)最低的Hadamard MDS 矩陣, 結(jié)果見(jiàn)表5.

表5 不同有限域中異或數(shù)最低的8×8 Hadamard MDS 矩陣Table 5 8 × 8 Hadamard MDS Matrices with lowest xor in different finite fields

5.3 優(yōu)化8 階Hadamard MDS 矩陣的搜索算法

最后, 我們對(duì)有限域中8 階Hadamard MDS 矩陣的搜索算法進(jìn)一步優(yōu)化.

首先利用交換環(huán)中4 階Hadamard 矩陣的判定方法. 由第4.2 節(jié)可知, 若M= Had(a1,a2,··· ,a8)是有限域F2n上的Hadamard MDS 矩陣,則M可以表示為Had(A1,A2,A3,A4),Ai=Had(a2i?1,a2i).該矩陣為交換環(huán)M 上的4 階Hadamard MDS 矩陣. 因此,σ1,σ4σ21+σ3σ2σ1+σ23,σ21σ4+σ23均為可逆元, 其中σk為交換環(huán)M 上的初等對(duì)稱(chēng)多項(xiàng)式. 我們首先判斷σ1,σ4σ21+σ3σ2σ1+σ23,σ21σ4+σ23是否可逆. 若其中存在某個(gè)元素不可逆, 則該8 階Hadamard 矩陣不是MDS 矩陣. 通過(guò)此方法可以快速過(guò)濾掉大量不是MDS 矩陣的候選矩陣. 然而直接計(jì)算這3 個(gè)元素, 過(guò)程依然比較繁瑣. 易知, 如果一個(gè)元素A可逆當(dāng)且僅當(dāng)A2可逆. 于是我們嘗試判定這3 個(gè)元素平方的可逆性. 令αi=a2i?1+a2i, 則有

其中,

綜上, 在交換環(huán)上判斷一個(gè)4 階Hadamard 矩陣的MDS 性質(zhì)需要進(jìn)行12 次加法和11 次乘法運(yùn)算.若M是一個(gè)對(duì)合矩陣則需要進(jìn)行4 次加法和9 次乘法運(yùn)算. 令集合S為{a1,a2,··· ,a8}, 其中ai是有限域F2n中的8 個(gè)互不相同的非零代表元. 利用集合S可以獲得8!個(gè)8 階Hadamard 矩陣. 將這些矩陣劃分為30 個(gè)等價(jià)類(lèi), 因此每一個(gè)等價(jià)類(lèi)含有1344 個(gè)8 階Hadamard 矩陣. 由這1344 個(gè)8 階Hadamard矩陣, 同樣可以獲得交換環(huán)M 上的1344 個(gè)4 階Hadamard 矩陣. 由命題7知, Had(A1,A2,A3,A4) 和Had(Ai1,Ai2,Ai3,Ai4) 在交換環(huán)M 上具有相同的MDS 矩陣的性質(zhì), 其中i1,i2,i3,i4是1,2,3,4 的置換. 因此, 又可以將這些矩陣分成= 56 類(lèi). 最后, 將這56 個(gè)矩陣全部列出, 最終排除相同的矩陣后只剩下7 個(gè)交換環(huán)上的4 階Hadamard 矩陣, 具體見(jiàn)表6. 若這7 個(gè)矩陣中存在矩陣不是交換環(huán)上4 階MDS 矩陣, 則這1344 個(gè)矩陣均不是有限域上的8 階Hadamard MDS 矩陣. 已知在交換環(huán)上判定一個(gè)4階對(duì)合Hadamard MDS 矩陣需要進(jìn)行4 次加法和9 次乘法運(yùn)算, 那么判斷這7 個(gè)矩陣則需要進(jìn)行28 次加法和63 次乘法運(yùn)算.

表6 用于第一步優(yōu)化搜索的7 個(gè)矩陣Table 6 7 matrices for optimizing search algorithm

其次, 我們發(fā)現(xiàn)對(duì)于8 階Hadamard 矩陣中存在4 階Hadamard 子矩陣. 當(dāng)8 階Hadamard 矩陣是一個(gè)MDS 矩陣, 則它所有4 階Hadamard 子矩陣也是MDS 矩陣. 因此我們可以利用5.1 的方法先對(duì)所有4 階Hadamard 子矩陣進(jìn)行判定. 若M=Had(a1,a2,··· ,a8) 是有限域F2n上的Hadamard MDS矩陣, 則M可以表示為Had(B1,B2), 其中B1=Had(a1,a2,a3,a4),B2=Had(a5,a6,a7,a8). 當(dāng)M是一個(gè)MDS 矩陣時(shí)B1和B2都必須是4 階Hadamard MDS. 除了B1和B2之外, 我們一共能找到14個(gè)關(guān)于M的4 階Hadamard 矩陣, 具體見(jiàn)表7. 最終由5.1 可知, 驗(yàn)證一個(gè)4 階的子方陣需要5 次加法和6 次乘法. 因此, 那么判斷這14 個(gè)矩陣則需要進(jìn)行70 次加法和84 次乘法運(yùn)算.

表7 用于第二步優(yōu)化搜索的14 個(gè)矩陣Table 7 14 matrices for optimizing search algorithm

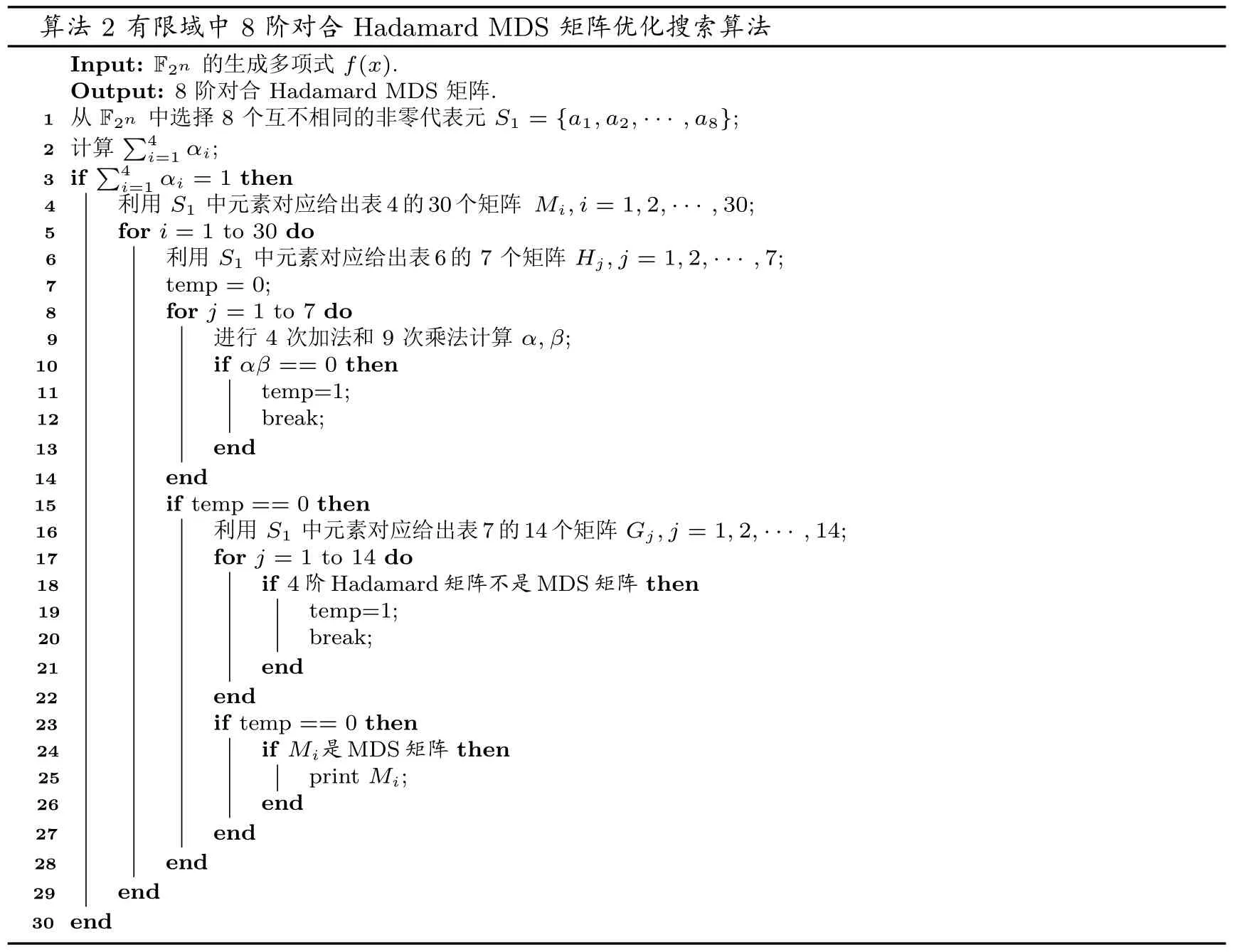
算法2 有限域中8 階對(duì)合Hadamard MDS 矩陣優(yōu)化搜索算法Input: F2n 的生成多項(xiàng)式f(x).Output: 8 階對(duì)合Hadamard MDS 矩陣.1 從F2n 中選擇8 個(gè)互不相同的非零代表元S1 = {a1,a2,··· ,a8};2 計(jì)算∑4 i=1 αi;3 if ∑4 i=1 αi = 1 then 6利用S1 中元素對(duì)應(yīng)給出表6 的7 個(gè)矩陣Hj,j = 1,2,··· ,7;4利用S1 中元素對(duì)應(yīng)給出表4 的30 個(gè)矩陣Mi,i = 1,2,··· ,30;5for i = 1 to 30 do 7 temp = 0;8 for j = 1 to 7 do進(jìn)行4 次加法和9 次乘法計(jì)算α,β;10if αβ == 0 then 9 11temp=1;12break;13end 14end 15if temp == 0 then 16利用S1 中元素對(duì)應(yīng)給出表7 的14 個(gè)矩陣Gj,j = 1,2,··· ,14;17for j = 1 to 14 do 18if 4 階Hadamard 矩陣不是MDS 矩陣then 19temp=1;20break;21end 22end 23if temp == 0 then 24if Mi是MDS 矩陣then 25print Mi;26end 27end 28end 29end 30 end

綜上所述, 我們可以對(duì)5.2 節(jié)給出的8 階Hadamard MDS 矩陣搜索方法進(jìn)行優(yōu)化, 即在對(duì)一個(gè)矩陣使用鏈?zhǔn)脚袆e法之前先檢驗(yàn)對(duì)應(yīng)的7 個(gè)矩陣是否是交換環(huán)上的4 階MDS 矩陣然后檢驗(yàn)14 個(gè)4 階Hadamard 矩陣是否為MDS 矩陣. 若存在非MDS 矩陣, 則該矩陣必然不是有限域上的8 階Hadamard MDS 矩陣, 無(wú)需再使用鏈?zhǔn)脚袆e法, 從而達(dá)到減少搜索空間的目的. 最后我們給出優(yōu)化后的8 階對(duì)合Hadamard MDS 矩陣的搜索算法2. 根據(jù)上述搜索策略, 我們?cè)谟邢抻騀26中進(jìn)行搜索, 在相同的計(jì)算條件下, 使用該優(yōu)化算法計(jì)算量減少了3 倍.

6 總結(jié)

在資源受限的環(huán)境中, 輕量級(jí)密碼算法的設(shè)計(jì)會(huì)更加注重硬件效率. Hadamard MDS 矩陣因其本身的良好性質(zhì), 被廣泛的應(yīng)用在線(xiàn)性層的設(shè)計(jì)中. 本文設(shè)計(jì)了一種Hadamard MDS 矩陣的快速搜索算法.

首先, 提出了MDS 矩陣的鏈?zhǔn)脚袆e法. 與高斯消元法相比, 該方法將子方陣行列式的計(jì)算復(fù)雜度從O(n3) 減小到O(n), 從而可以快速的驗(yàn)證矩陣的MDS 性質(zhì). 隨著矩陣階數(shù)增大, 計(jì)算效率的提升也更加顯著.

其次,給出了有限域上m(m=4,8)階Hadamard MDS 矩陣的判定方法. 對(duì)于4 階Hadamard 矩陣,只需要驗(yàn)證3 個(gè)元素是否為0 即可判斷該矩陣是否為MDS 矩陣. 該方法有效地提升了4 階Hadamard MDS 矩陣的搜索效率, 并且還可以被推廣到有限交換環(huán)上. 對(duì)于8 階Hadamard 矩陣, 只需要判定不小于4 階子方陣均滿(mǎn)秩, 即可判定該矩陣為Hadamard MDS 矩陣. 該方法將待計(jì)算的子方陣行列式的個(gè)數(shù)減少了一半, 因此可以更加快速的判定8 階Hadamard MDS 矩陣.

最后, 結(jié)合上述方法, 本文給出了有限域上m(m= 4,8) 階Hadamard MDS 矩陣的快速搜索算法.對(duì)于一個(gè)給定的4 階Hadamard 矩陣, 只需要計(jì)算6 次乘法和5 次加法即可確定該矩陣是否為MDS矩陣. 利用該判定方法可以窮搜有限域F2n(n ≤8) 上的4 階Hadamard MDS 矩陣, 并且搜索到了F2n(n ≤16) 上異或數(shù)最低的4 階Hadamard MDS 矩陣. 對(duì)于有限域上8 階Hadamard 矩陣, 我們利用有限交換環(huán)上4 階Hadamard 矩陣和有限域上8 階Hadamard 矩陣的聯(lián)系減小搜索范圍. 最終, 實(shí)現(xiàn)了對(duì)有限域F2n(n ≤6) 上8 階Hadamard MDS 矩陣的窮搜, 并且搜索到了F2n(n ≤16) 上異或數(shù)最低的Hadamard MDS 矩陣.