知識庫的相對約簡與拓?fù)浼s簡

吳國俊,徐羅山

(揚州大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,江蘇揚州 225002)

§1 引言

粗糙集理論[1]首先由Pawlak提出,是用于處理不確定性知識的數(shù)學(xué)工具.在粗糙集理論中,知識約簡是重要的課題,也是獲取知識的重要步驟.論域U上的知識指U上的某個等價關(guān)系,知識庫指的是U上的一族等價關(guān)系,文獻[2]論述了知識庫的多種約簡理論.趙靜,徐羅山在文獻[3]中研究了知識庫的知識約簡和知識表達系統(tǒng)的屬性約簡的轉(zhuǎn)化和聯(lián)系.王長忠等在文獻[4]中把知識庫推廣為關(guān)系信息系統(tǒng),它實際為U上的一族二元關(guān)系.文獻[5]則把U上的任一子集族稱為一個抽象知識庫.本文強調(diào)與抽象知識庫的區(qū)別,把關(guān)系信息系統(tǒng)仍稱為知識庫.李旭等在文[6]中定義了相對不可區(qū)分關(guān)系約簡和相對區(qū)分關(guān)系約簡.本文對知識庫提出相對約簡概念,給出有限知識庫相對約簡的求法.文獻[7-13]將拓?fù)鋵W(xué)方法引入到粗糙集的研究中,提出了關(guān)系誘導(dǎo)拓?fù)?其中文獻[12-13]利用拓?fù)鋵W(xué)方法討論了知識的多種約簡.本文借助關(guān)系誘導(dǎo)拓?fù)涮岢鐾負(fù)浼s簡的概念,探討交約簡,相對約簡和拓?fù)浼s簡的關(guān)系及其求法.

§2 預(yù)備知識

本文用P(U)表示U的冪集,U上的恒等關(guān)系△={(x,x)|x ∈U},又稱為對角關(guān)系.用|·|表示集合的基數(shù),無特別說明,約定|U|＞1.

設(shè)R是U上的二元關(guān)系.則序?qū)?U,R)稱為一個廣義近似空間.對x ∈U,記Rs(x)={y ∈U |xRy}與Rp(x)={y ∈U |yRx}.U上自反又傳遞的二元關(guān)系稱為一個預(yù)序.

定義2.1[7-11]廣義近似空間(U,R)中的下近似算子和上近似算子分別定義為:P(U)→P(U)使得

引理2.1[8]設(shè)(U,R)是廣義近似空間,則為U上的Alexandrov拓?fù)?并稱該拓?fù)錇?U,R)的關(guān)系誘導(dǎo)拓?fù)?

定義2.2[11]設(shè)R是論域U上的二元關(guān)系,包含R的最小預(yù)序稱為R的預(yù)序閉包,記為p(R).

注2.1容易驗證(1)R ?p(R)=p(p(R))且p(R)=△∪R ∪R2∪R3∪···.

(2) 設(shè)R,Q是論域U上的二元關(guān)系,若Q ?R,則p(Q)?p(R).

命題2.1設(shè)R1,R2是U上的二元關(guān)系,R1?R2.則p(R1)=p(R2)當(dāng)且僅當(dāng)R2?p(R1).

證必要性: 因R2?p(R2),故由p(R1)=p(R2)知,R2?p(R1).

充分性: 因R1?R2?p(R1),故由注2.1知p(R1)?p(R2)?p(p(R1))=p(R1),從而p(R1)=p(R2).

引理2.2[11]設(shè)(U,R1),(U,R1)是兩廣義近似空間,則TR1=TR2當(dāng)且僅當(dāng)p(R1)=p(R2).

定義2.3[14](1) 設(shè)R是U上的一族二元關(guān)系.則(U,R)稱為U上的知識庫,也簡稱R是U上的知識庫.交集∩R=∩P ∈R P稱為R的不可區(qū)分知識,記作ind(R).(2) 設(shè)R是U上的知識庫,Q ?R且.若ind(Q)=ind(R)且對Q的任一非空真子集Q0,ind(Q)ind(Q0),則Q稱為R的交約簡.R的全體交約簡用red(R)表示.

(3) 設(shè)R是U上的知識庫.當(dāng)|R|＞1時,稱集族{R ∈R|ind(R-{R})ind(R)}為R的核,記為core(R).當(dāng)|R|=1時,約定core(R)=R.

§3 知識庫的相對約簡與RM-區(qū)分矩陣

本節(jié)給出知識庫相對約簡與RM-區(qū)分矩陣的概念,并研究它們的相關(guān)性質(zhì).關(guān)于有限偏序集的結(jié)論可參見文獻[15].

定義3.1設(shè)R是U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q.若存在使ind(P)?Q,且對P的任一非空真子集P0,有,則稱P是R相對于Q的交約簡,簡稱Q-相對約簡.R的全體Q-相對約簡可用redQ(R)表示.

注3.1由定義2.3和3.1知R的交約簡就是R的ind(R)-相對約簡,即red(R)=redind(R)(R).這說明交約簡是特殊的相對約簡.當(dāng)該定義中涉及的二元關(guān)系均為等價關(guān)系且論域U是有限集時,定義3.1中R的Q-相對約簡就是文[2]中Q關(guān)于R相對依賴度為1的Q-相對約簡.

命題3.1設(shè)R是有限集U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,則R存在Q-相對約簡,即redQ(R).

證作A={P ?R |ind(P).因R ∈A,故.因(A,?)是非空有限偏序集,故其每個鏈L都存在最小元.由Zorn引理知(A,?)存在極小元P0,則ind(P0)?Q.又由P0的極小性知P0的任一非空真子集均不含于Q.這說明P0∈redQ(R).

注3.2命題3.1的證明過程實際上給出了求相對約簡的極小元方法: 構(gòu)造偏序集A={P ?R|ind(P),求出(A,?)的所有極小元,它們恰好是R的全體Q-相對約簡.對于論域無窮的情形,容易舉例說明(相對)約簡不一定存在.

定義3.2設(shè)R是U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q.當(dāng)|R| ＞1時,若存在R ∈R使,則稱R為R的Q-相對核心元素,稱為R的Q-相對核,記為coreQ(R).當(dāng)|R|=1時,約定coreQ(R)=R.

命題3.2設(shè)R是U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q.則coreQ(R)?core(R).

證當(dāng)|R|=1時,顯然.下面設(shè)|R| ＞1.若R ∈coreQ(R),則因ind(R)?Q,故ind(R-{R})ind(R),從而R ∈core(R).于是coreQ(R)?core(R).

定理3.1設(shè)R是有限集U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,則coreQ(R)=∩redQ(R).

證當(dāng)|R|=1時,顯然.下面對|R| ＞1先證明coreQ(R)?∩redQ(R),用反證法.若存在R ∈coreQ(R)使R/∈∩redQ(R),則存在Q ∈redQ(R)使R/∈Q.于是Q ?R-{R},從而ind(R)?ind(R -{R})?ind(Q).由Q ∈redQ(R)知,ind(Q)?Q,由ind(R -{R})?ind(Q)得ind(R-{R})?Q,這與R ∈coreQ(R) 矛盾.再證明∩redQ(R)?coreQ(R),用反證法.若存在R ∈∩redQ(R)使R/∈coreQ(R),則ind(R-{R})?Q.任取Q0∈redQ(R-{R}),可推得Q0∈redQ(R)且R/∈Q0,這與R ∈∩redQ(R)矛盾.綜上所證,coreQ(R)=∩redQ(R).

定義3.3設(shè)R是上知識庫,Q是U上二元關(guān)系且ind(R)?Q,?xi,xj ∈U,記

則稱矩陣DQ(U,R)=(rij)n×n是R相對于Q的RM-區(qū)分矩陣.

命題3.3設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,DQ(U,R)是R相對于Q的RM-區(qū)分矩陣.若,則ind(P)?Q當(dāng)且僅當(dāng)?rij ∈DQ(U,R),P∩rij ?.

證必要性: 對任一rij ∈DQ(U,R),若xj ∈Qs(xi),則rij=R,此時P ∩rij=.若xj/∈Qs(xi),則(xi,xj)/∈Q.由ind(P)?Q知,(xi,xj)/∈ind(P),從而存在R ∈P使(xi,xj)/∈R,即xj/∈Rs(xi),這說明R ∈P ∩rij,于是P ∩rij ?.

充分性: 若(xi,xj)/∈Q,則xj/∈Qs(xi),此時rij={R ∈R|xj/∈Rs(xi)}.由P ∩rij ?知存在R ∈P,使xj/∈Rs(xi),即(xi,xj)/∈R ∈P,從而(xi,xj)/∈ind(P).由(xi,xj)/∈Q的任意性知,ind(P)?Q.

推論3.1設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,DQ(U,R)是R相對于Q的RM-區(qū)分矩陣.則?rij ∈DQ(U,R),有rij ?.

證由ind(R)?Q及命題3.3知,?rij ∈DQ(U,R),R ∩rij ?,從而rij ?.

定理3.2設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,DQ(U,R)是R相對于Q的RM-區(qū)分矩陣.若,則P是R的Q-相對約簡當(dāng)且僅當(dāng)對P是滿足?rij ∈DQ(U,R),P ∩rij ?這一性質(zhì)的R的極小子族.

證由定義3.1及命題3.3直接驗證.

下一定理表明可以利用RM-區(qū)分矩陣求有限知識庫R的相對核.

定理3.3設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,DQ(U,R)=(rij)n×n是R相對于Q的RM-區(qū)分矩陣.則coreQ(R)={R ∈R|?i,j≤n,rij={R}}.

證當(dāng)|R|=1時,顯然.下面設(shè)|R| ＞1.記S={R ∈R | ?i,j≤n,rij={R}}.先證S ?coreQ(R),用反證法.設(shè)存在R ∈S使R/∈coreQ(R),則存在rij ∈DQ(U,R)使rij={R}且ind(R-{R})?Q.由命題3.3知(R-{R})∩rij ?,從而存在Q0∈R-{R}使Q0∈rij,這與rij={R}矛盾.下面證明coreQ(R)?S.若Q1∈coreQ(R),則.由命題3.3知存在rij ∈DQ(U,R)使(R-{Q1})∩rij=?.從而由推論3.1得rij={Q1},于是Q1∈S.由Q1∈coreQ(R)的任意性知coreQ(R)?S.綜上,定理得證.

§4 知識庫的拓?fù)浼s簡

設(shè)R是U的知識庫,則(U,ind(R))是廣義近似空間,記(U,ind(R))的關(guān)系誘導(dǎo)拓?fù)錇門ind(R).本節(jié)給出知識庫拓?fù)浼s簡的定義,并探討它與相對約簡的關(guān)系.

定義4.1(1) 設(shè)R是U上的知識庫,.若Tind(Q)=Tind(R)且對Q的任一非空真子集Q0,都有Tind(Q0)ind(R),則稱Q為R的一個拓?fù)浼s簡.R的全體拓?fù)浼s簡用redT(R)表示.

(2) 設(shè)R是U上的知識庫,R ∈R.當(dāng)|R| ＞1時,若Tind(R-{R})ind(R),則稱R是R的拓?fù)浜诵脑?稱集{R ∈R | Tind(R-{R})ind(R)}為R的拓?fù)浜?記作coreT(R).當(dāng)|R|=1時,約定coreT(R)=R.

命題4.1若R是論域U上的一族預(yù)序,則red(R)=redT(R).

證當(dāng)|R|=1時,顯然.下面對|R|＞1先證red(R)?redT(R).若Q ∈red(R),則ind(Q)=ind(R),因R是論域U上的一族預(yù)序,故ind(Q)及ind(R)是U上的預(yù)序.于是由ind(Q)=ind(R)知p(ind(Q))=p(ind(R)).從而由引理2.2知Tind(Q)=Tind(R).因Q ∈red(R),故對Q的任一非空真子集Q0,有ind(Q0)ind(R).由R是論域U上的一族預(yù)序知p(ind(Q0))(ind(R)).從而由引理2.2知Tind(Q0)ind(R).這說明Q ∈redT(R).由Q ∈red(R)的任意性知red(R)?redT(R).

red(R)?redT(R)逆推可得.綜上,red(R)=redT(R).

下面定理表明知識庫的拓?fù)浼s簡是特殊的相對約簡.

定理4.1設(shè)R是U上的知識庫,R ∈R,.則

(1)Q是R的拓?fù)浼s簡當(dāng)且僅當(dāng)Q是R的p(ind(R))-相對約簡;

(2)R是R的拓?fù)浜诵脑禺?dāng)且僅當(dāng)R是R的p(ind(R))-相對核心元素.

證下面以(1)為例證之,(2)類似可證明.

充分性: 若Q是R的拓?fù)浼s簡,則Tind(Q)=Tind(R)且對Q的任一非空真子集Q0,Tind(Q0)ind(R).由引理2.2知p(ind(Q))=p(ind(R))且p(ind(Q0))(ind(R)).由命題2.1得ind(Q)?p(ind(R))且.這說明Q是R的p(ind(R))-相對約簡.

必要性: 由引理2.2,命題2.1逆推可得.

推論4.1設(shè)R是有限集U上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,則

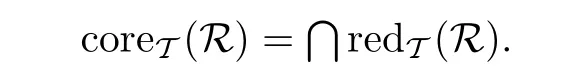
證由定理3.1,4.1直接驗證.

下一命題表明,對有限知識庫R中的每一成員適當(dāng)擴充,不影響拓?fù)浼s簡和拓?fù)浜说臉?gòu)成.

命題4.2設(shè)R={R1,R2,···,Rm}是有限集U上的知識庫,△={(x,x)| x ∈U}是U上的恒等關(guān)系.給定△i ?△(i=1,2,···,m),作R*={R1∪△1,R2∪△2,···,Rm ∪△m}.則

(1)Q*={Rj1∪△j1,Rj2∪△j2,···,Rjs ∪△js}∈redT(R*)當(dāng)且僅當(dāng)

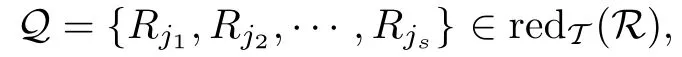
其中Rjt ∈R(t=1,2,···,s且s ＞1);

(2)coreT R*={Ri1∪△i1,Ri2∪△i2,···,Rik∪△ik}當(dāng)且僅當(dāng)coreT R={Ri1,Ri2,···,Rik},其中Rit ∈R(t=1,2,···,k且k ＞1).

證先證(1).必要性: 因Q*={Rj1∪△j1,Rj2∪△j2,···,Rjs ∪△js} ∈redT(R*),故Tind(Q*)=Tind(R*),從而由引理2.2知p(ind(Q*))=p(ind(R*)).因ind(Q)?ind(Q*)?△∪ind(Q),故由注2.1得,p(ind(Q))?p(ind(Q*))?p(△∪ind(Q))=p(ind(Q)).從而p(ind(Q))=p(ind(Q*)).同理有p(ind(R))=p(ind(R*)),從而p(ind(Q))=p(ind(R)).由引理2.2得Tind(Q)=Tind(R).又?Rjt ∈Q,有Rjt ∪△jt ∈Q*.因Q* ∈redT(R*),故Tind(Q*-{Rjt∪△jt})ind(R*),從而p(Q*-{Rjt ∪△jt})(R*).由ind(Q-{Rjt})?ind(Q*-{Rjt ∪△jt})?△∪ind(Q-{Rjt})及注2.1可推得p(ind(Q*-{Rjt ∪△jt}))=p(ind(Q-{Rjt})).從而p(ind(Q-{Rjt}))(ind(R*))=p(ind(R)),進而Tind(Q-{Rjt})ind(R),這說明Q ∈redT(R).

充分性: 逆推可得.

(2)由(1)及推論4.1直接驗證.

§5 知識庫相對約簡的求法

本節(jié)到布爾函數(shù)方面的相關(guān)知識,讀者可參考文獻[2]或其它相關(guān)文獻.

定義5.1設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,DQ(U,R)=(rij)n×n是R相對于Q的RM-區(qū)分矩陣.稱布爾函數(shù)為R的相對于Q的RM-區(qū)分函數(shù).

定義5.2設(shè)R是上的知識庫,Q是U上的二元關(guān)系且

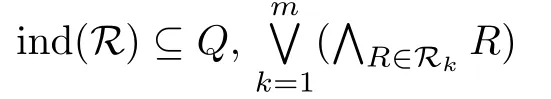
是RM-區(qū)分函數(shù)fQ(R)的某一析取范式.若中無重復(fù)元素,且?k,j≤m當(dāng)時,Rk與Rj互不包含,則稱該析取范式為fQ(R)的極小析取范式.

定理5.1設(shè)R是上的知識庫,Q是U上的二元關(guān)系且ind(R)?Q,.若為R的相對于Q的RM-區(qū)分函數(shù)fQ(R)的極小析取范式,則P ∈redQ(R)當(dāng)且僅當(dāng)存在k≤m使P=Rk.

證類似于文[4]定理4.7的證明,從略.

注5.1定理5.1給出了相對約簡的具體求法: 將fQ(R)化為極小析取范式則{Rk |k=1,2,···,m}恰是知識庫R的全部Q-相對約簡.

下面以例說明求有限知識庫相對約簡(包括交約簡,拓?fù)浼s簡)的方法.

例5.1設(shè)U={xi |1 ≤i≤8},R={Rk |1 ≤k≤5}為U上的知識庫,其中

易得ind(R)={(x1,x2),(x2,x3),(x4,x5),(x5,x6)}.

下面用極小元方法求R的交約簡,它們是特殊的相對約簡.先由注3.2求得偏序集

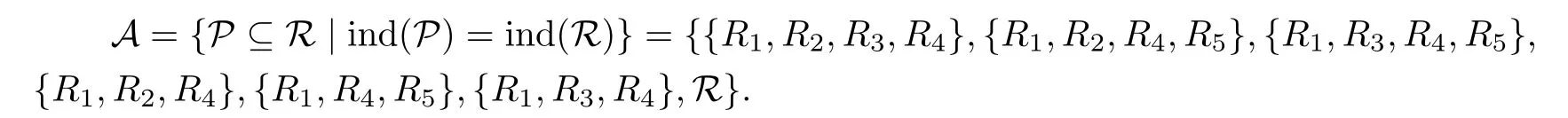
A的極小元即為R的交約簡,red(R)={{R1,R2,R4},{R1,R3,R4},{R1,R4,R5}}.注意到交約簡是特殊的相對約簡,由定理3.1又可得core(R)={R1,R4}.

設(shè)Q={(x1,x2),(x2,x3),(x1,x3),(x4,x5),(x5,x6),(x7,x8)}是U上二元關(guān)系,則ind(R)?Q.下面用RM-區(qū)分矩陣和RM-區(qū)分函數(shù)求R的Q-相對約簡及Q-相對核.

作R的相對于Q的RM-區(qū)分矩陣DQ(U,R)如表5.1,為了簡潔,用Ri的下標(biāo)i代替Ri,例如r61={2,3,5}代表r61={R2,R3,R5}.R代表{1,2,···,5}.

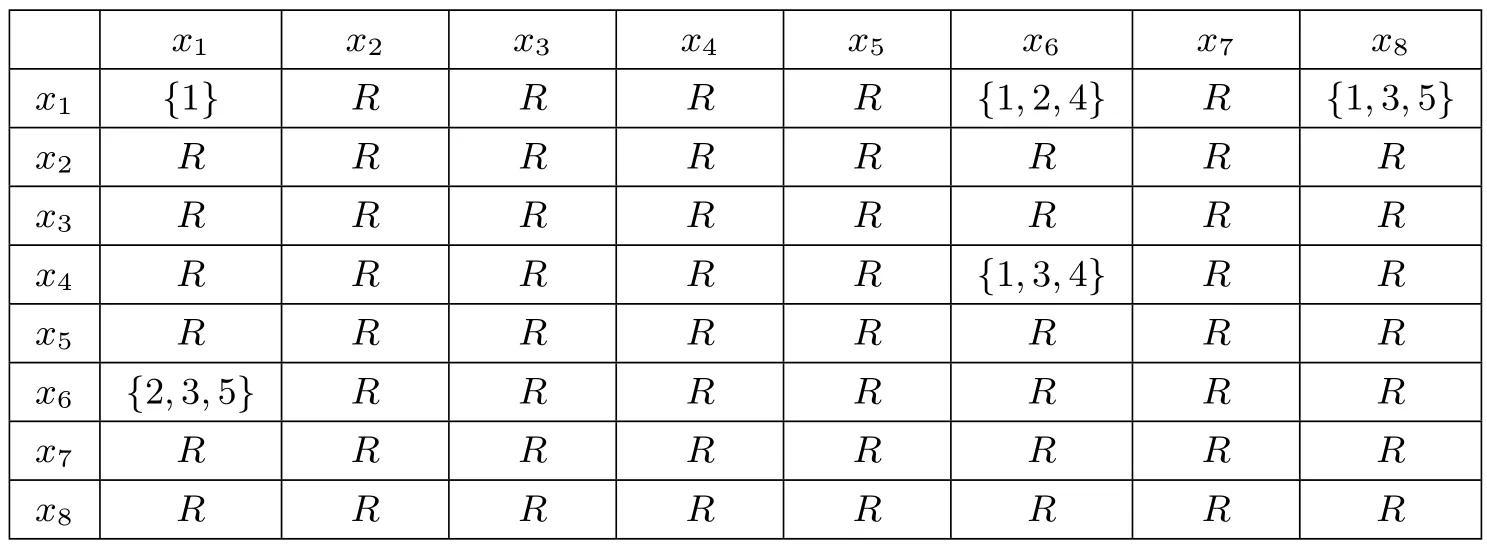
表5.1 RM-區(qū)分矩陣DQ(U,R)

將R的相對于Q的RM-區(qū)分函數(shù)化為極小析取范式

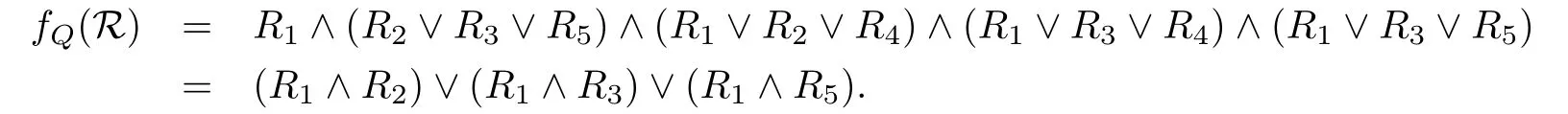
由定理5.1知R的全體Q-相對約簡為redQ(R)={{R1,R2},{R1,R3},{R1,R5}};由定理3.3知R的Q-相對核為coreQ(R)={R1}.

下面用RM-區(qū)分矩陣和RM-區(qū)分函數(shù)求R的拓?fù)浼s簡(特殊的相對約簡)及拓?fù)浜?

由定理4.1,先求得p(ind(R))={(x1,x2),(x1,x3),(x2,x3),(x4,x5),(x4,x6),(x5,x6)}∪△.

作R的相對于p(ind(R))的RM-區(qū)分矩陣Dp(ind(R))(U,R)如表5.2.為了簡潔,用Ri的下標(biāo)i代替Ri,例如r61={2,3,5}表示的是r61={R2,R3,R5}.R代表{1,2,···,5}.

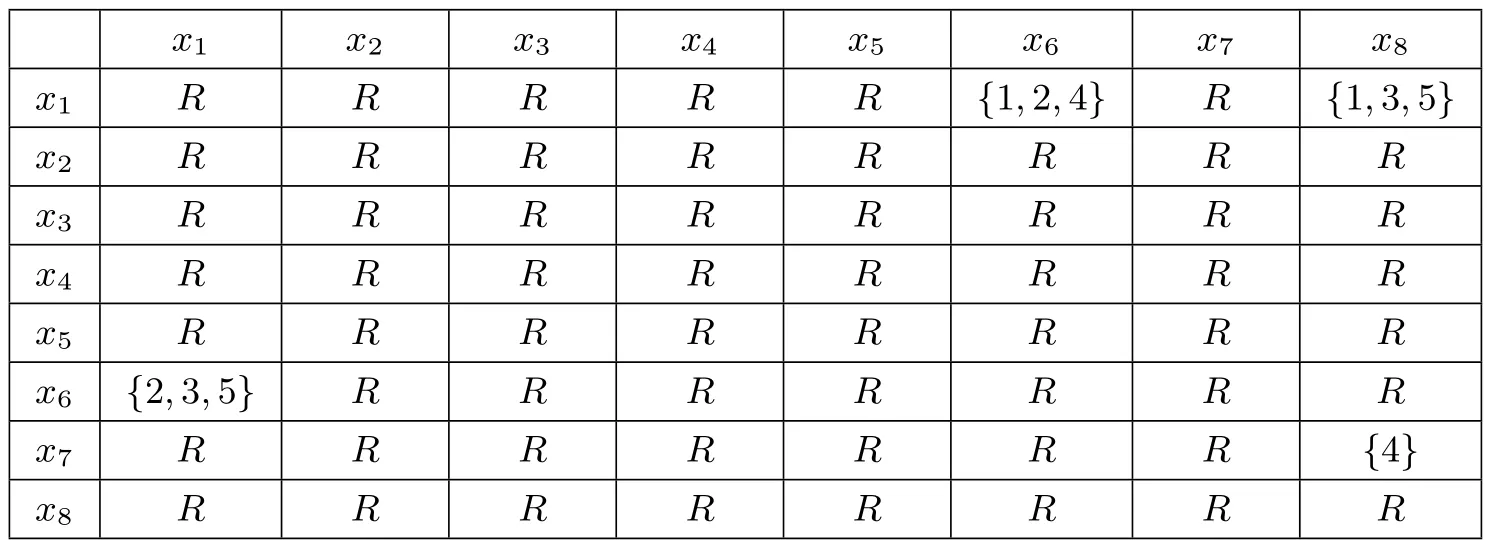
表5.2 RM-區(qū)分矩陣Dp(ind(R))(U,R)

將R的相對于p(ind(R))的RM-區(qū)分函數(shù)化為極小析取范式

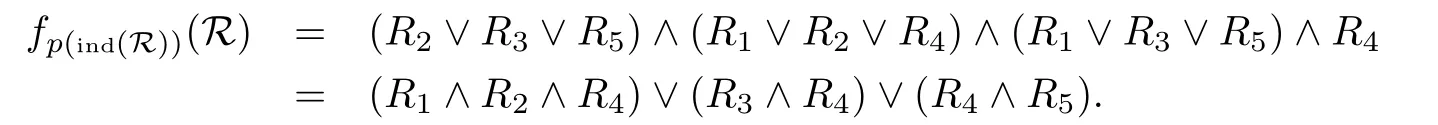
由定理4.1和5.1知R的拓?fù)浼s簡全體為redT(R)={{R1,R2,R4},{R3,R4},{R4,R5}};由定理3.3和定理4.1知R的拓?fù)浜藶閏oreT(R)={R4}.