一類特殊笛卡爾乘積網(wǎng)絡(luò)的泛圈性
張治成
(石河子大學(xué) 理學(xué)院,新疆石河子 832003)
§1 引言
互連網(wǎng)絡(luò)是超級(jí)計(jì)算機(jī)的重要組成部分,在很大程度上決定著超級(jí)計(jì)算機(jī)的性能,其拓?fù)浣Y(jié)構(gòu)是指超大規(guī)模計(jì)算機(jī)系統(tǒng)中的元件(處理器)的連接模式.互連網(wǎng)絡(luò)的結(jié)構(gòu)和性質(zhì)是超級(jí)計(jì)算機(jī)研究的重要課題.在設(shè)計(jì)和選擇一個(gè)互連網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)時(shí),Hamilton性,泛圈性,連通度,直徑等指標(biāo)對(duì)分析網(wǎng)絡(luò)性能發(fā)揮了重要作用.
在分析網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)時(shí),通常將互連網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)模型化為一個(gè)無向圖,圖的頂點(diǎn)對(duì)應(yīng)處理器,圖的邊對(duì)應(yīng)網(wǎng)絡(luò)的通訊鏈路[1-4].因而在研究互連網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)時(shí),往往通過研究一個(gè)無向圖來深入研究互連網(wǎng)絡(luò).互連網(wǎng)絡(luò)拓?fù)涞男阅芸梢酝ㄟ^圖的性能和指標(biāo)來度量,如Hamilton性,嵌入性,容錯(cuò)性,泛圈性等[1-12].因此,圖論是設(shè)計(jì)和分析互連網(wǎng)絡(luò)最基本且強(qiáng)有力的工具.
圖嵌入是一個(gè)客圖到一個(gè)主圖的映射,它保留了一些被要求的性質(zhì).如果一個(gè)客圖能夠嵌入到一個(gè)主圖,那就意味著在客圖網(wǎng)絡(luò)上能夠執(zhí)行的算法同樣能夠在主圖網(wǎng)絡(luò)上模擬執(zhí)行.在眾多的互連網(wǎng)絡(luò)拓?fù)渲?路和圈是最為基礎(chǔ),也是最為重要的兩種網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu).在路和圈網(wǎng)絡(luò)中,容易設(shè)計(jì)出簡(jiǎn)單而又高效的路由算法.因此,在設(shè)計(jì)和選擇互連網(wǎng)絡(luò)時(shí)路和圈的可嵌入性是一個(gè)非常重要的考慮因素.近年來,Bondy提出了泛圈性問題,即尋找所有可能長(zhǎng)度的圈[1].泛圈性是判斷一個(gè)網(wǎng)絡(luò)拓?fù)涫欠襁m合將不同長(zhǎng)度的圈映射到其上的重要測(cè)量值.圈的嵌入是對(duì)互連網(wǎng)絡(luò)的圖嵌入問題研究的重點(diǎn)之一,它可以用圖的泛圈性和邊泛圈性來衡量.
在大規(guī)模并行系統(tǒng)中,互連網(wǎng)絡(luò)在硬件成本,通信性能,高效算法和容錯(cuò)能力方面扮演著重要的角色.近年來,學(xué)者們提出了許多互連網(wǎng)絡(luò)拓?fù)?笛卡爾乘積網(wǎng)絡(luò)DSCC(k)×K2是師海忠等提出的一類重要的互連網(wǎng)絡(luò)拓?fù)鋄5-6],由于它具有較好的正則性,連通性,Hamilton性等性質(zhì),從而為大規(guī)模超級(jí)計(jì)算機(jī)系統(tǒng)和互連網(wǎng)絡(luò)的優(yōu)化設(shè)計(jì)提供了理論參考價(jià)值,得到了廣泛的關(guān)注和研究.
§2 預(yù)備知識(shí)
下面介紹文中用到的一些基本知識(shí).
定義2.1[1-2]設(shè)G=(V,E)是一個(gè)圖,下述概念中頂點(diǎn)均取自V,邊均取自E.如果在圖G中點(diǎn)v是邊e的一個(gè)端點(diǎn),則稱頂點(diǎn)v與邊e在圖G中相關(guān)聯(lián);如果圖上兩點(diǎn)u,v被同一條邊相連,則稱u,v在圖G中相鄰;若圖G中兩條邊有至少一個(gè)公共端點(diǎn),則稱這兩條邊在圖G相鄰;端點(diǎn)重合為一點(diǎn)的邊稱為環(huán);端點(diǎn)不相同的邊稱為連桿;設(shè)u和v是圖G的頂點(diǎn),圖G中連接u和v的兩條或兩條以上的邊稱為圖G中u,v間的重邊或平行邊;既無環(huán)邊也無重邊的圖稱為簡(jiǎn)單圖;|V|和|E|都是有限的圖稱為有限圖(finite graph).本文只考慮有限無向簡(jiǎn)單圖.用圖表示互連網(wǎng)絡(luò)時(shí),頂點(diǎn)代表網(wǎng)絡(luò)節(jié)點(diǎn)(處理器),邊代表節(jié)點(diǎn)之間直接的通信連接.
定義2.2[1-2]設(shè)G是一個(gè)無向圖,G中一個(gè)點(diǎn)邊連續(xù)交替出現(xiàn)的序列ω=v0e1v1e2···vkek稱為圖G的一條途徑,其中v0和vk分別稱為途徑ω的起點(diǎn)和終點(diǎn),ω上其余頂點(diǎn)稱為中途點(diǎn);圖G中邊不重復(fù)出現(xiàn)的途徑稱為跡;頂點(diǎn)不重復(fù)出現(xiàn)的跡稱為路,起點(diǎn)和終點(diǎn)相同的途徑稱為閉途徑,邊不重復(fù)出現(xiàn)的閉途徑稱為閉跡,中途點(diǎn)不重復(fù)出現(xiàn)的閉跡稱為圈;經(jīng)過圖G的每個(gè)頂點(diǎn)一次的圈稱為一個(gè)Hamilton圈,記為H.
定義2.3[1-2]若一個(gè)圖具有這樣的一個(gè)圖形,它的邊僅在端點(diǎn)處相交,則該圖稱為平面圖.設(shè)x和y是G中的兩頂點(diǎn),如果G中存在xy路,那么稱x和y在G中是連通的.若一個(gè)圖中任意兩個(gè)頂點(diǎn)之間都有一條Hamilton 路,則稱這個(gè)圖為Hamilton連通圖.
定義2.4[1-2]設(shè)G1=(V1,E1)和G2=(V2,E2)是兩個(gè)無向圖.G1和G2的笛卡爾乘積(Cartesian product)是無向圖,記為G1×G2,其中V(G1×G2)=V1×V2={(v1,v2)|v1∈V1且v2∈V2},兩個(gè)不同的頂點(diǎn)(x1,x2) 和(y1,y2)(其中x1,y1∈V(G1),x2,y2∈V(G2))相鄰當(dāng)且僅當(dāng)或者x1=y1且x2y2∈E(G2),或者x2=y2且x1y1∈E(G1).
定義2.5[4]設(shè)G是n階圖,如果G中存在任意長(zhǎng)為l(3≤l ≤n)的圈,則G稱為泛圈的;如果在G中,對(duì)于任意一個(gè)頂點(diǎn)v,存在任意長(zhǎng)為l(3≤l ≤n)的包含v的圈,則G稱為點(diǎn)泛圈的;如果在G中,對(duì)于任意一條邊e,存在任意長(zhǎng)為l(3≤l ≤n)的包含e的圈,則G稱為邊泛圈的.在一個(gè)n階二部圖G中,如果G中存在任意長(zhǎng)為偶數(shù)l(4≤l ≤n)的圈,則G稱為偶泛圈的;如果在G中,對(duì)于任意一個(gè)頂點(diǎn)v,存在任意長(zhǎng)為偶數(shù)l(4≤l ≤n)的包含v的圈,則G稱為點(diǎn)偶泛圈的;如果在G中,對(duì)于任意一條邊e,存在任意長(zhǎng)為偶數(shù)l(4≤l ≤n)的包含e的圈,則G稱為邊偶泛圈的.
定義2.6[5]將十二面體連通圈網(wǎng)絡(luò)中的每個(gè)頂點(diǎn)用一個(gè)三角形(3長(zhǎng)的圈C3)來代替,且三角形的每個(gè)頂點(diǎn)僅位于十二面體中與該頂點(diǎn)關(guān)聯(lián)的一條邊上,得到的新網(wǎng)絡(luò)稱為1次十二面體-師連通圈網(wǎng)絡(luò),記為DSCC(1);再將1次十二面體-師連通圈網(wǎng)絡(luò)DSCC(1)中的每個(gè)頂點(diǎn)用一個(gè)三角形來代替,且三角形的每個(gè)頂點(diǎn)僅位于DSCC(1)中與該頂點(diǎn)關(guān)聯(lián)的一條邊上,得到的新網(wǎng)絡(luò)稱為2次十二面體-師連通圈網(wǎng)絡(luò),記為DSCC(2);重復(fù)代替k次,得到的新網(wǎng)絡(luò)稱為k次十二面體-師連通圈網(wǎng)絡(luò),記為DSCC(k).
定義2.7[6]將k次十二面體-師連通圈網(wǎng)絡(luò)DSCC(k)與K2的笛卡爾乘積定義為無向圖,生成是新網(wǎng)絡(luò)稱為笛卡爾乘積網(wǎng)絡(luò)DSCC(k)×K2.
引理2.1[6]DSCC(0)×K2是偶泛圈的.
引理2.2[6]DSCC(k)×K2是偶泛圈的.
§3 主要結(jié)果
通過引理2.1和2.2的結(jié)果,提出一個(gè)更一般性的結(jié)論,對(duì)于任意Hamilton平面連通圖,它與K2的笛卡爾乘積圖都有引理2.2的結(jié)果成立.結(jié)論的具體內(nèi)容及其證明以定理的形式給出如下:
定理3.1任何一個(gè)Hamilton平面連通圖G與K2的笛卡爾乘積G×K2都是偶泛圈的.
證設(shè)G=(V(G),E(G))是一個(gè)n階的Hamilton平面連通圖,其中
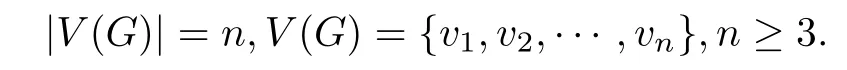
設(shè)G的一個(gè)Hamilton圈HG=v1v2···vi···vj···vnv1,其中1≤i,j ≤n.作出G×K2如圖3.1所示,圖中是HG的一個(gè)復(fù)制,HG和之間的邊是序號(hào)相同的對(duì)應(yīng)頂點(diǎn)之間的匹配,|V(G×K2)|=2n.在圈HG和中不相鄰頂點(diǎn)之間的邊未畫出,因?yàn)檫@些邊在G×K2中不影響它的偶泛圈性.
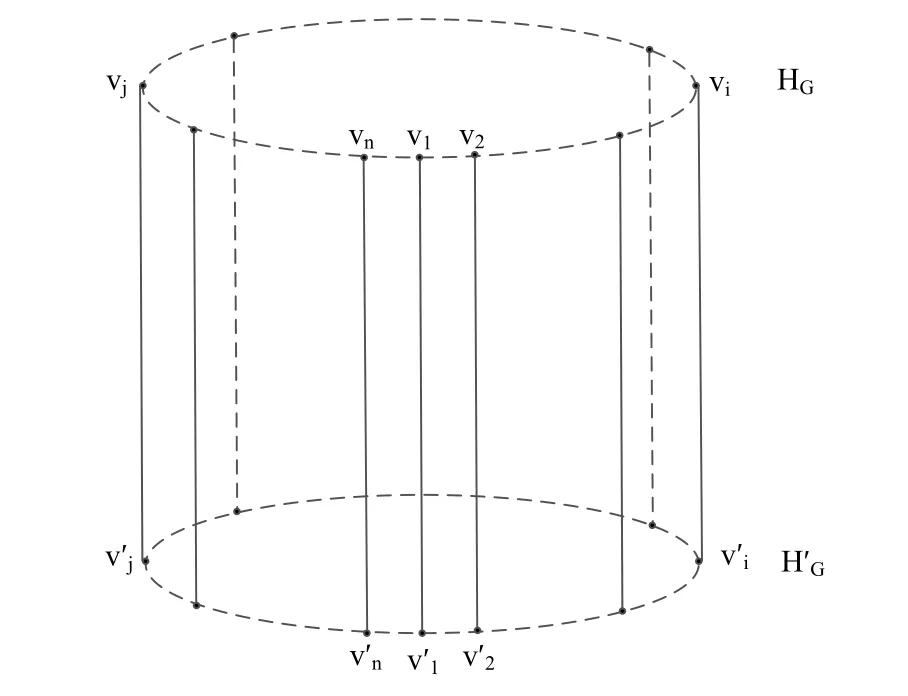
圖3.1 DSCC(k)×K2
根據(jù)偶泛圈性的定義,只需證明G×K2中存在任意偶數(shù)長(zhǎng)度l(4≤l ≤2n) 的圈即可.選擇以邊作為起始邊,不妨假設(shè)i=1,以為起始邊,向右依次找長(zhǎng)為l的偶圈.在G×K2中觀察到,圈長(zhǎng)l是頂點(diǎn)序數(shù)i的兩倍,利用在HG和中的序數(shù)i同時(shí)逐次遞增的方式,找到包含邊的所有偶數(shù)長(zhǎng)度l(4≤l ≤2n)的圈如下.
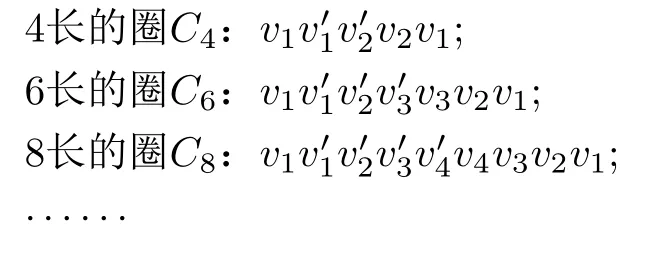
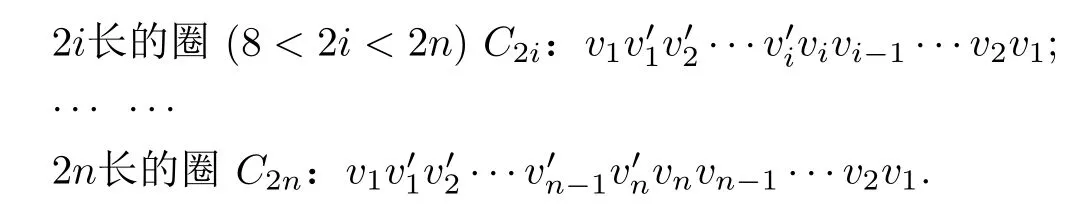
因此G×K2中存在長(zhǎng)為4到2n的所有偶圈,故笛卡爾乘積G×K2是偶泛圈的.
下面討論DSCC(k)×K2的泛圈性.當(dāng)k ≥1時(shí),DSCC(k)×K2的泛圈性如下.
定理3.2DSCC(k)×K2(k ≥1)是泛圈的.
證由泛圈性的定義知,只需證明DSCC(k)× K2(k ≥1)中存在任意長(zhǎng)為l(3≤l ≤40×3k)的圈.根據(jù)圈長(zhǎng)l的奇偶性,分為兩種情形來討論這些圈的存在性.
情形1 當(dāng)l是偶數(shù)時(shí),記m=l.
證明DSCC(k)×K2(k ≥1)中存在任意長(zhǎng)為偶數(shù)m(3≤m ≤40×3k,m=4,6,···,40×3k)的偶圈,即證DSCC(k)×K2是偶泛圈的.根據(jù)定理3.1的結(jié)果,由于DSCC(k)是Hamilton平面連通圖,所以DSCC(k)×K2是偶泛圈的.所以當(dāng)l是偶數(shù)m時(shí),所有m長(zhǎng)的偶圈都是存在的.
情形2 當(dāng)l是奇數(shù)時(shí),記n=l.
證明DSCC(k)×K2(k ≥1)中存在任意長(zhǎng)為奇數(shù)n(3≤n ≤40×3k,n=3,5,···,40×3k-1)的奇圈.當(dāng)n=3時(shí),因?yàn)镈SCC(k)是由DSCC(k-1)中的每一個(gè)頂點(diǎn)被一個(gè)三角形代替得到的,所以DSCC(k)×K2中顯然存在3 長(zhǎng)的圈C3.
當(dāng)n >3時(shí),接著證明DSCC(k)×K2中存在任意長(zhǎng)為n(5≤n ≤40×3k -1)的所有奇圈Cn.在情形1中,證明了DSCC(k)×K2中存在長(zhǎng)為偶數(shù)m(4≤m ≤40×3k -2)的所有偶圈.現(xiàn)在任取其中的一個(gè)偶圈,記為Cm,通過偶圈Cm來構(gòu)造出奇圈Cn=Cm+1.首先,顯然DSCC(k)×K2中的每個(gè)頂點(diǎn)都是某一個(gè)三角形的頂點(diǎn),故在找到m長(zhǎng)的偶圈Cm中,它的每個(gè)頂點(diǎn)也是屬于某一個(gè)三角形的.
其次,在構(gòu)造偶圈Cm的過程中,在滿足其條件的情況下,總能使得找到的圈Cm中存在至少一個(gè)這樣的情況,那就是Cm(m為偶數(shù))當(dāng)且僅當(dāng)包含某一個(gè)三角形中的兩個(gè)頂點(diǎn).假設(shè)這個(gè)三角形的頂點(diǎn)分別是vi1,vi2和vi3,包含在Cm中的頂點(diǎn)是vi1和vi2.此時(shí)把第三個(gè)頂點(diǎn)嵌入到偶圈Cm中,就能得到奇圈Cm+1,如圖3.2所示.由m的任意性可知,在DSCC(k)×K2中能由偶圈Cm(4≤m ≤40×3k -2)構(gòu)造出長(zhǎng)為奇數(shù)n=m+1 (5≤n ≤40×3k -1)的所有奇圈.故當(dāng)l是奇數(shù)n時(shí),所有n長(zhǎng)的奇圈都是存在的.
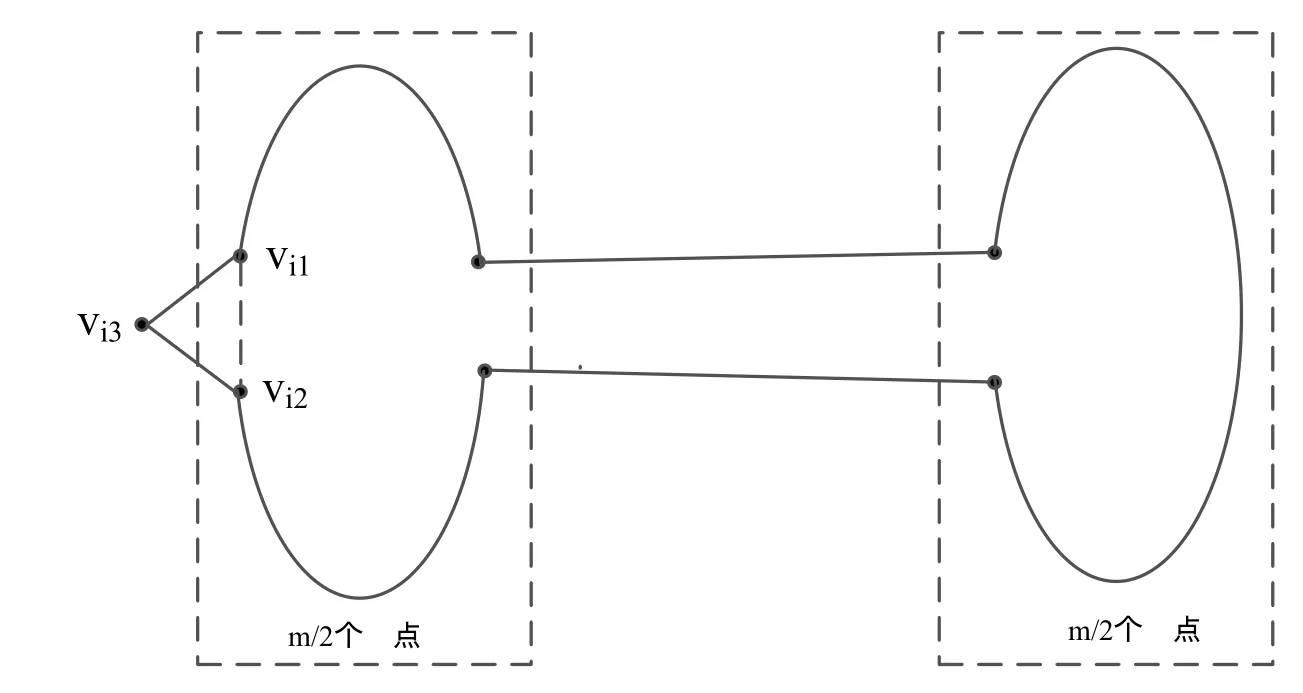
圖3.2 Cm+1
綜合以上所有情形,知道DSCC(k)×K2(k ≥1)中存在任意長(zhǎng)為l(3≤l ≤40×3k) 的圈,即DSCC(k)×K2(k ≥1)是泛圈的.

